返回顶部

规则内联

在本主题中

  1. 语法
  2. 参数
  3. 描述
  4. 相关内容
  5. 示例

语法

  • inline Rule
  • inline subdivision
  • inline { operations }
  • inline(geometryMergeStrategy) Rule
  • inline(geometryMergeStrategy) subdivision
  • inline(geometryMergeStrategy) { operations }

参数

  1. geometryMergeStrategy - selector
    定义对生成形状的几何进行组合的方式：
    • append - 默认值。 按原样附加几何。
    • unify - 使用布尔 union 操作。
  2. 语法选项：
    • Rule - 规则的名称。
    • subdivision - 细分操作（请参阅几何细分）。
    • { operations } - 花括号中的一系列形状操作。

描述

inline 关键字用于触发指定规则、细分操作或形状操作序列的即时派生。 然后将生成的形状自动合并为用于替换当前形状的单个形状。 如果其生成单个形状，则可以按原样进行合并。 如果其生成多个形状，则将根据 geometryMergeStrategy 对其几何进行组合。 默认情况下（如果未指定任何策略），则将仅附加几何。

如果内联形状具有冲突的材料属性，则会将每个形状的材料写入几何，这意味着将保留所有材料。 对于其他属性，如果内联形状具有冲突的值或者进行了多个 set 操作，则将保留当前形状的值。

概念

这是初始形状。

初始形状

将对初始形状应用两个规则：Volumes 用于分割形状并插入不同的资产，而 Colorize 用于设置黄色。 这些规则将独立修改输入形状，并且不会相互影响。

可以在模型等级中观察到这一点，其中两个规则均代表单独形状子树的根。 完整形状树中的叶子形状将共同形成可见模型。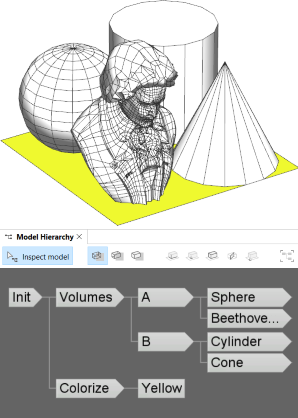

Init -->
    Volumes
    Colorize

Colorize --> color(1,1,0) Yellow.

Volumes --> split(x) { '0.5: A | '0.5: B }
    
A --> split(z) { '0.5: Sphere   | '0.5: Beethoven }
B --> split(z) { '0.5: Cylinder | '0.5: Cone }
    
Sphere    --> primitiveSphere
Cylinder  --> primitiveCylinder
Cone      --> primitiveCone
Beethoven --> i("beethoven.obj")
应用于初始形状的体积和着色规则。

通过内联 Volumes，可以按顺序排列两个规则，从而允许 Colorize 将 Volumes 的组合结果作为输入。

本质上，内联规则的使用方式与内置形状操作（例如，extrude）类似，用于直接修改当前形状。

Init -->
    inline Volumes
    Colorize

将折叠并从模型等级中移除内联规则（例如 Volumes）生成的子树，从而控制派生顺序以及形状树的结构。

按顺序排列两个规则的内联体量

几何合并策略

正确的 geometryMergeStrategy 将取决于建模目标。 目前，提供了两种策略：

  • append

    默认值。 用于简单采集多个形状的几何并将其放入单个网格中。 将不会执行任何几何清理，并且所有组件保持原样。

  • unify

    用于将相交形状的几何与布尔操作相结合。 将以拓扑方式连接相交的面，并移除内部面。

相关内容

  • union, subtract, intersect 操作
  • tag 操作
  • 几何标签：基础知识

示例

网格拓扑

Init -->
    primitiveCube
    print("start: " + geometry.nVertices)
    inline comp(f) { all: SetColor }
    print("inlined: " + geometry.nVertices)
    cleanupGeometry(vertices, 0)
    print("cleanup: " + geometry.nVertices)
    
rampValue = comp.index/comp.total
SetColor -->
    set(material.opacity, 0.9)
    color(colorRamp("spectrum", rampValue))

内联用于将立方体的着色面组合为单个形状。 仅附加这些面，因此其不会共享折点。 可以使用 cleanupGeometry 进行修复。

网格拓扑

F 型建筑物

Init -->
    split(z, noAdjust) 
        {  7: split(x) { ~7: House | 7: House }*
        | ~1: split(x) { ~7: NIL   | 7: House }* }

House --> 
    extrude(5)
    comp(f) { side: Fac. | top: roofGable(40) Roof. }

不使用内联：将初始形状分割为 F 形状。 将单独对每个部分进行拉伸，并在顶部建造一个独立、分离的屋顶。

内联前的 F 型建筑物
Init -->
    inline FShapePieces
    cleanupGeometry(all, 0)
    House
	
FShapePieces -->
    split(z, noAdjust) 
        {  7: split(x) { ~7: Done. | 7: Done. }*
        | ~1: split(x) { ~7: NIL   | 7: Done. }* }

使用内联：FShapePieces 规则为内联规则，由此可将所有部分组合为单个形状。 如果使用 append，则几何将保持不变，这意味着这些部分不是通过共享边进行连接。 要连接这些部分并将其合并为单个覆盖区面，可以使用 cleanupGeometry 操作。 由此将生成单个拉伸体量和单个接缝屋顶。

内联后的 F 型建筑物

两种选择中的最佳选择

Init --> 
    inline {
        [ tag("LayoutA") LayoutA ]
        [ tag("LayoutB") LayoutB ]
    }
    ChooseLayout

LayoutA --> offset(-15, border)
LayoutB --> split(x) { 15: Lot. | ~10: NIL }*

taggedArea(name) = 
    sum(comp(f) { isTagged(name): geometry.area })

ChooseLayout -->
    case taggedArea("LayoutA") > taggedArea("LayoutB"):
          comp(f) { isTagged("LayoutA")= Mass }
    else: comp(f) { isTagged("LayoutB")= Mass }

Mass --> extrude(30)

将生成两个不同的标记布局。 如果使用 inline(append)，则会将其组合为单个形状。 然后，可以使用 comp 函数和标签来比较两个布局的面积，并且仅继续使用较大的布局。

使用内联进行组合的标记布局

统一螺旋台阶

Init --> 
    inline(unify) StepsRec(18)
    color(0, 1, 0, 0.8)

StepsRec(nSteps) -->
    case nSteps > 0: 
        Step
        r(0, 20, 0)
        t(0, 0.18, 0)
        StepsRec(nSteps-1)
    else: 
        NIL
        
Step -->  s(0.4, 0.3, 1) primitiveCube

StepsRec(nSteps) 规则将递归生成螺旋楼梯的台阶。 当使用 unify 内联规则时，可将这些台阶组合为单个形状，并使用 3D 布尔 union 操作将其几何合并为单个密封网格。

统一螺旋台阶

内联和标签

Init -->
    inline(unify) split(x) { 3: A | 4: B | 3: C }
    comp(f) { isTagged("A"): Blue
            | isTagged("B"): Yellow
            | isTagged("C"): Red }
	
A --> primitiveCylinder tag("A")
B --> t(-1, 0.5, 0.75)  
      s(6, 2, 1.5)
      primitiveCube
      tag("B")
C --> primitiveSphere tag("C")

可将初始形状分割为 3 个部分，不同的基本几何资产将插入每个部分，然后对其进行标记。 使用 unify 内联 split 可将其合并到单个密封网格中，同时保留单个面组件上的标签。

3D 中的内联标签
Init -->
    inline(unify) split(x) { 3: A | 4: B | 3: C }
    comp(f) { isTagged("A") && isTagged("B"): Green 
            | isTagged("B") && isTagged("C"): Orange
            | isTagged("A")                 : Blue
            | isTagged("B")                 : Yellow
            | isTagged("C")                 : Red }

A --> primitiveDisk tag("A")
B --> t(-1, 0, 0.75)  
      s(6, 0, 1.5)
      tag("B")
C --> tag("C")

Blue -->   color("#0399F5")
Green -->  color("#09DE1F")
Yellow --> color("#FADB19")
Red -->    color("#FF360A")
Orange --> color("#FA9100")

2D 中的相同示例。 将保留所有原始边和标签，由此可使用标签标识相交部分。

2D 中的内联标签

有关此主题的反馈?

在本主题中
  1. 语法
  2. 参数
  3. 描述
  4. 相关内容
  5. 示例