A ferramenta Parâmetros da Superfície determina os parâmetros de uma superfície raster, como aspecto, declividade e curvatura.
Aspecto
O parâmetro de superfície Aspecto identifica a direção voltada para a inclinação da declividade. O valor de cada célula no raster de saída indica a direção da bússola voltada para a superfície neste local. É medido no sentido horário em graus de 0 (no norte) a 360 (novamente no norte), fechando o círculo. Áreas planas sem direção descendente recebem um valor de -1.

As imagens a seguir mostram um conjunto de dados de elevação de entrada e o raster de aspecto de saída.
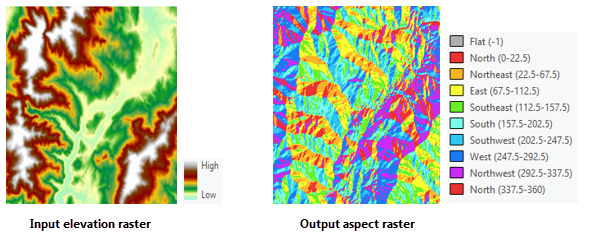
Aplicações do aspecto
Com o tipo de parâmetro da superfície Aspecto, você pode fazer o seguinte:
- Encontrar todas as pistas voltadas para o norte em uma montanha como parte de uma busca pelas melhores inclinações para pistas de esqui.
- Calcular a iluminação solar para cada local em uma região como parte de um estudo para determinar a diversidade da vida em cada local.
- Encontrar todas as encostas ao sul em uma região montanhosa para identificar os locais onde a neve provavelmente derreterá primeiro como parte de um estudo para identificar os locais residenciais que provavelmente serão atingidos primeiro pelo escoamento.
Cálculos de aspecto geodésico
O aspecto geodésico em um local é a direção angular α da superfície descendente em relação ao norte, medida em um plano tangente à superfície do elipsóide (o plano azul na ilustração abaixo).

Para calcular o aspecto em cada local, uma superfície quadrática ou biquadrática é ajustada às células da vizinhança usando o Método dos Mínimos Quadrados (LSM). Uma normal de superfície é calculada na localização da célula a partir dessa superfície. No mesmo local, uma normal do elipsóide perpendicular ao plano tangente da superfície do elipsóide também é calculada.
Como o plano tangente da superfície do elipsóide é considerado o plano de referência, a normal da superfície é projetada no plano. Finalmente, o aspecto geodésico é calculado medindo-se o ângulo α no sentido horário entre o norte e a projeção da superfície normal (veja a ilustração acima).
Declividade
O parâmetro de superfície Declividade é a inclinação em cada célula de uma superfície raster. Quanto menor o valor da inclinação, mais plano é o terreno; quanto maior o valor da inclinação, mais íngreme o terreno.
O raster de inclinação de saída pode ser calculado em qualquer uma das duas unidades, graus ou porcentagem (aumento percentual). O aumento percentual é melhor compreendido se você o considerar como o aumento dividido pela execução, multiplicado por 100. Considere o triângulo B abaixo. Quando o ângulo é de 45 graus, a elevação é igual à corrida e a porcentagem de elevação é de 100%. À medida que o ângulo de inclinação se aproxima da vertical (90 graus), como no triângulo C, o aumento percentual começa a se aproximar do infinito.

A inclinação é executada com mais frequência em um conjunto de dados de elevação, como mostram as imagens a seguir. Inclinações mais íngremes são sombreadas em marrom mais escuro no raster de inclinação de saída.

A ferramenta também pode ser usada com outros tipos de dados contínuos, como população, para identificar mudanças bruscas de valor.
Cálculos de declividade geodésica
A declividade geodésica é o ângulo formado entre a superfície topográfica e a superfície do elipsóide. Qualquer superfície paralela à superfície do elipsóide tem uma inclinação de 0. Para calcular a declividade em cada local, uma superfície quadrática ou biquadrática é ajustada às células da vizinhança usando o Método dos Mínimos Quadrados (LSM). Uma normal de superfície é calculada na localização da célula a partir dessa superfície. No mesmo local, uma normal do elipsóide perpendicular ao plano tangente da superfície do elipsóide também é calculada. A inclinação, em graus, é calculada a partir do ângulo entre a normal do elipsóide e a normal da superfície topográfica. Este ângulo é o mesmo entre a superfície topográfica e a superfície do elipsóide.
Visão geral da superfície de curvatura
Curvatura é uma coleção de tipos de parâmetros da superfície usados para descrever a forma de uma superfície, normalmente ao longo de uma linha na superfície, criada pela intersecção de um plano através da superfície. Conceitualmente, a curvatura geométrica encontra o círculo de melhor ajuste (círculo osculante) para aproximar a forma da curva em qualquer ponto. A curvatura é o recíproco do raio desse círculo (1/r). Uma linha mais reta se ajustará melhor a um círculo maior, resultando em uma curvatura menor, e uma linha curva mais estreita se ajustará melhor a um círculo menor, resultando em uma curvatura maior (Crane, 2018).

Curvatura de perfil (linha de declividade normal)
O parâmetro de superfície Curvatura de perfil (linha de inclinação normal) mede a curvatura normal geométrica ao longo da linha de inclinação. Às vezes denominada curvatura de perfil, ela pode ser visualizada como a forma de uma seção transversal vertical (perfil) através da superfície. Conforme ilustrado abaixo, o plano vertical corta a superfície ao longo da linha laranja e, se for cortado, aparecerá como um perfil de seção transversal da superfície.

Esse plano é definido por dois vetores, a seta amarela mostrando a direção do gradiente ou a seta da linha de inclinação e a seta vermelha indicando a superfície normal. É a combinação desses vetores vermelho e amarelo que define o plano laranja e sua linha laranja de intersecção com a superfície. A curvatura de perfil é calculada ao longo da linha laranja (linha de inclinação normal) no plano laranja.
A terminologia de Minár et al da linha de inclinação normal (2020) é usada aqui para minimizar a ambiguidade e confusão com a terminologia anterior.
Essa curvatura é normalmente aplicada para caracterizar a aceleração e desaceleração do fluxo na superfície pela força da gravidade. Em velocidades mais altas, a água pode carregar e mover grandes quantidades de material; áreas de aceleração tornam-se áreas de erosão e áreas de desaceleração tornam-se áreas de deposição.
Na imagem abaixo, as áreas de curvatura de alto perfil convexo (linha de inclinação normal) ao redor da crista do cone são mostradas em roxo. Áreas de curvatura de alto perfil côncavo (linha de inclinação normal) na base do cone são mostradas em laranja. Áreas com pequenos valores de curvatura são transparentes.

Os resultados desta curvatura são diferentes na saída da curvatura de Perfil da ferramenta Curvatura anterior. Uma explicação das diferenças entre a curvatura de Perfil e a curvatura de Perfil (linha de inclinação) é fornecida posteriormente.
A fórmula para calcular a curvatura do perfil (linha de inclinação normal) é a seguinte:

- Onde:
KP = Curvatura de perfil (linha de inclinação normal)
z = f(x,y)
Curvatura tangencial (contorno normal)
O parâmetro de superfície Curvatura tangencial (curva de nível normal) mede a curvatura normal geométrica perpendicular à linha de inclinação, tangente à linha de contorno. É referido como a curvatura tangencial, pois mede a curvatura tangente à linha de contorno. É descrito como contorno normal (Minár et al., 2020) pois o plano de corte roxo que cria a linha roxa ao longo da qual a curvatura é calculada é definido pelo vetor de contorno azul e pelo vetor de superfície normal vermelho.

A curvatura tangencial (contorno normal) é normalmente aplicada para caracterizar a convergência topográfica e a divergência do fluxo através da superfície.
Na imagem abaixo, as áreas de alta curvatura tangencial convexa (contorno normal) ao redor da aresta do cone e a aresta voltada para você são mostradas em azul. Estas são áreas de fluxo divergente. Áreas de alta curvatura tangencial côncava (contorno normal) dentro do cone mostram o fluxo convergente em vermelho. Áreas com pequenos valores de curvatura são transparentes.

A fórmula para calcular a curvatura tangencial (contorno normal) é a seguinte:

- Onde:
KT = Curvatura tangencial (contorno normal)
z = f(x,y)
Curvatura do plano (contorno projetado)
O parâmetro de superfície Curvatura do plano (contorno projetado) mede a curvatura ao longo das linhas de contorno. Às vezes é referido como curvatura de contorno e curvatura horizontal. A curvatura de contorno projetado é medida ao longo da linha de contorno em azul, onde o plano horizontal intercepta a superfície.

A fórmula para calcular a curvatura do plano (contorno projetado) é a seguinte:

- Onde:
KPC = Curvatura do plano (contorno projetado)
z = f(x,y)
A imagem abaixo ilustra a diferença entre a curvatura tangencial (contorno normal), medida ao longo da linha roxa, e a curvatura plana (contorno projetado), medida ao longo da linha de contorno azul.

Torção geodésica de contorno
O parâmetro de superfície Torção geodésica de contorno mede a taxa de mudança no ângulo de inclinação ao longo das linhas de contorno.
A fórmula para calcular a torção geodésica de contorno é a seguinte:

- Onde:
τ = Torção geodésica de contorno
z = f(x,y)
Curvatura média
O parâmetro de superfície Curvatura média mede a curvatura geral da superfície. É calculado como a média da curvatura mínima e máxima. Também é matematicamente equivalente à média das curvaturas de Perfil (linha de inclinação normal) e Tangencial (contorno normal). Na imagem abaixo, o plano de corte do Perfil (linha de inclinação normal) (laranja) e o plano de corte Tangencial (contorno normal) (roxo) são mostrados.

A curvatura de perfil (linha de inclinação normal) e tangencial (contorno normal) mede a convexidade e a concavidade em uma direção específica; enquanto a curvatura média descreve a convexidade ou concavidade intrínseca da superfície, independente da direção ou influência da gravidade. Seu sinal (positivo ou negativo) não é um indicador definitivo de convexidade ou concavidade, exceto em valores extremos, pois uma superfície pode ser côncava em uma direção e também convexa em outra. Valores positivos altos indicam áreas de desnudamento máximo e valores negativos altos indicam áreas de acúmulo máximo (Minár et al., 2020).
A fórmula para calcular a curvatura Média é a seguinte:

- Onde:
KM = Curvatura média
z = f(x,y)
Curvatura Gaussiana
O parâmetro de superfície Curvatura Gaussiana mede a curvatura geral de uma superfície. É calculado como o produto da curvatura mínima e máxima e pode assumir valores negativos e positivos. Valores positivos indicam que a superfície é convexa naquela célula e valores negativos indicam que ela é côncava. Um valor de 0 indica que a superfície é plana.
A fórmula para calcular a curvatura Gaussiana é a seguinte:

- Onde:
KG = Curvatura Gaussiana
z = f(x,y)
Curvatura de Casorati
O parâmetro de superfície Curvatura de Casorati mede a curvatura geral de uma superfície. Pode ser zero ou qualquer outro número positivo. Valores positivos altos indicam áreas de dobra acentuada em várias direções.
A fórmula para calcular a curvatura Casorati é a seguinte:

- Onde:
KC = Curvatura de Casorati
z = f(x,y)
Tipos de curvatura básica e combinatória
A curvatura Tangencial (contorno normal), a curvatura de Perfil (linha de inclinação normal) e a torção geodésica de contorno são consideradas tipos básicos de curvatura, pois outras curvaturas podem ser expressas como uma combinação delas. Adotando a terminologia de Minár et al (2020), são descritos como o trio Básico.
Além das expressões fornecidas acima para curvatura média, curvatura Gaussiana e curvatura de Casorati, essas curvaturas também podem ser calculadas como uma combinação do trio Básico.
A fórmula para calcular a curvatura Média é a seguinte:

- Onde:
KM = Curvatura média
KT = Curvatura tangencial (contorno normal)
KP = Curvatura de perfil (linha de inclinação normal)
z = f(x,y)
A fórmula para calcular a curvatura Gaussiana é a seguinte:

- Onde:
KG = Curvatura Gaussiana
KT = Curvatura tangencial (contorno normal)
KP = Curvatura de perfil (linha de inclinação normal)
τ = Torção geodésica de contorno
z = f(x,y)
A fórmula para calcular a curvatura Casorati é a seguinte:

- Onde:
KC = Curvatura de Casorati
KM = Curvatura média
KG = Curvatura Gaussiana
z = f(x,y)
Comparação com algoritmos antigos da ferramenta Curvatura
A ferramenta Parâmetros da Superfície usa algoritmos de curvatura diferentes da ferramenta Curvatura, como também, matemática geodésica em seus cálculos; portanto, nenhuma comparação direta de resultados entre essas duas ferramentas deve ser feita. Os tipos de curvatura dos Parâmetros da Superfície, Perfil (linha de inclinação normal) e Tangencial (contorno normal), são verdadeiras curvaturas geométricas (Minár et al. 2020). A curvatura média da ferramenta Parâmetros da Superfície é a média da curvatura mínima e máxima neste ponto. Os tipos Perfil e Formulário de Plano da ferramenta Curvatura são derivadas direcionais, não medindo de fato a curvatura geométrica da superfície em um local (Zevenbergen e Thorne 1987) O sinal (positivo ou negativo) para Perfil (linha de inclinação normal) na ferramenta Parâmetros da Superfície é oposto à curvatura de perfil da ferramenta Curvatura. A ferramenta Parâmetros da Superfície calcula no espaço geodésico, e a ferramenta Curvatura usa coordenadas planares e matemática. A ferramenta Parâmetros da Superfície pode ajustar uma superfície quadrática ou biquadrática, a ferramenta Curvatura suporta apenas biquadrática.
Distância de vizinhança
O valor Distância de vizinhança é a distância do mapa a partir do centro da célula de processamento atual até o centro de um vizinho ortogonal. Uma distância de vizinhança menor captura mais variabilidade local na paisagem, o que produz características de feições de paisagem menores. Com dados de elevação de resolução mais alta, uma distância de vizinhança maior pode ser mais apropriada devido ao erro de escala fina (ruído) nos dados que não refletem os processos do relevo de interesse ou porquê o relevo de interesse é mais reconhecível em distâncias maiores.
O exemplo abaixo usou um modelo de superfície digital (DSM) com resolução de 5 metros que apresenta ruído perceptível e artefatos de listras exibidos no resultado da curvatura de perfil (linha de inclinação normal). A primeira imagem usou a janela padrão de 3 x 3 ou distância de vizinhança de 5 metros, a segunda imagem é uma janela de célula de 9 x 9 ou distância de vizinhança de 20 metros e a terceira imagem usou uma janela de célula de 15 x 15 ou distância de vizinhança de 35 metros. Neste exemplo, com o aumento da distância de vizinhança, as feições mais significativas ou primárias da paisagem tornam-se mais claras e, o ruído e artefatos de listras são menos visíveis. Embora uma distância de vizinhança maior sempre resulte em menos ruído, a distância mais apropriada dependerá do tamanho da célula dos dados e do tamanho das feições do relevo que são importantes para a aplicação.

A menor distância de vizinhança é igual ao tamanho da célula do raster de entrada. A maior distância de vizinhança é igual a sete vezes o tamanho da célula, resultando em uma janela de células de 15 x 15. Qualquer distância especificada maior que sete vezes o tamanho da célula sempre resultará no uso de uma janela de célula de 15 x 15.

Se for especificada uma distância de vizinhança que não resulte em um intervalo ímpar do tamanho da célula, ela será arredondada para o próximo intervalo do tamanho da célula. Por exemplo, na ilustração acima, se uma distância de vizinhança de 25 metros foi especificada, ela arredondará para o próximo intervalo do tamanho da célula, 30 metros (três vezes o tamanho da célula), resultando em uma janela de células de 7 x 7.
Se os dados de elevação tiverem uma resolução espacial muito mais precisa do que o necessário para analisar as formas de relevo de interesse, uma alternativa à opção da janela de vizinhança é reamostrar ou agregar os dados a um tamanho de célula maior que seja mais apropriado para a aplicação.
Os cálculos de parâmetros da superfície são sensíveis ao tamanho da célula e à distância de vizinhança. Wilson (2018) e Minár et al (2020) fornecem resumos eficazes e atualizados dos numerosos estudos sobre esse tópico.
Vizinhança adaptável
Quando marcado, o parâmetro Usar vizinhança adaptável altera a distância de vizinhança (tamanho ou área da janela) usada para calcular o parâmetro da superfície para capturar melhor a variação relevante na paisagem. A ferramenta determina automaticamente o tamanho apropriado da janela calculando o desvio local da elevação média (DEV) (Wilson e Gallant, 2000) com base nos valores de todas as células dentro da vizinhança. Ela tenta usar o maior tamanho de janela possível, minimizando a variabilidade da superfície (James et al., 2014). O maior tamanho de janela usado é especificado no parâmetro Distância de vizinhança.
Ao calcular o parâmetro da superfície com uma vizinhança fixa, todos os valores de célula dentro da vizinhança são usados. Ao calcular o parâmetro da superfície com uma vizinhança adaptável, apenas nove células (as células ortogonais e diagonais externas e a célula central de processamento) da vizinhança são usadas.

A vizinhança adaptável é particularmente útil ao analisar uma paisagem com feições do terreno de tamanhos amplamente variados, como grandes colinas onduladas com pequenos barrancos ou canais de riachos, a partir de um DEM de alta resolução. Em tal situação, uma pequena distância de vizinhança, como 1 metro, pode ser usada para as ravinas do riacho e uma distância maior da vizinhança de 10 ou 15 metros usada para as colinas.
Na ilustração abaixo, uma vizinhança menor é apropriada para o riacho e a borda do penhasco, uma vizinhança maior para a transição da colina para a planície e uma vizinhança ainda maior para o platô homogêneo quase plano.

Efeito de borda da distância de vizinhança
As células ao redor da borda externa da saída serão atribuídas ao NoData quando informações insuficientes estiverem disponíveis para o cálculo.
Ao usar a opção de vizinhança adaptável, a extensão do raster de saída diminuirá em torno de sua borda externa em uma célula.
Ao usar uma distância de vizinhança fixa maior que o tamanho da célula de entrada, a extensão do raster de saída será reduzida de acordo com a distância de vizinhança usada. A quantidade de redução pode ser calculada como (largura da janela em pixels - 1) / 2
Por exemplo, se a distância de vizinhança resultar no uso de uma janela de células 7 x 7, o raster de saída diminuirá em torno de sua borda externa em três células.
Quadrático e biquadrático
Há dois tipos de superfícies locais que podem ser ajustadas à janela de vizinhança, quadrática e biquadrática. O padrão é quadrática e é recomendado para a maioria dos dados e aplicativos.
A superfície quadrática é um ajuste de mínimos quadrados dos pontos e não passa exatamente por todos os pontos. Ao não passar exatamente por todos os pontos, o uso da superfície quadrática tem o efeito de minimizar o impacto de dados de superfície ruidosos, como uma superfície lidar de alta resolução. Isso cria um resultado mais representativo para todos os parâmetros de superfície e é especialmente importante ao calcular a curvatura.
A superfície quadrática deve ser usada ao especificar um tamanho de vizinhança maior que o tamanho da célula e ao usar a opção de vizinhança adaptável.
A superfície biquadrática se ajusta exatamente aos dados das células vizinhas. Esta opção é adequada para uma superfície de entrada altamente precisa, livre de ruído aleatório. Se a distância de vizinhança for maior que o tamanho da célula raster de entrada, as vantagens de precisão do tipo de superfície biquadrática serão perdidas; portanto, a distância de vizinhança deve ser deixada como padrão (igual ao tamanho da célula).
Transformação de coordenadas geodésicas
A ferramenta Parâmetros da Superfície realiza seus cálculos em um sistema de coordenadas 3D geocêntrico, também denominado sistema de coordenadas Earth Centered, Earth Fixed (ECEF), considerando a forma da Terra como um elipsóide. O resultado do cálculo não é afetado pela forma como o conjunto de dados é projetado. Ele usará as unidades z do raster de entrada se elas forem definidas na referência espacial. Se a referência espacial de entrada não definir as unidades z, você precisará fazer isso com o parâmetro de unidade z.
O sistema de coordenadas ECEF é um sistema de coordenadas cartesianas destras 3D com o centro da Terra como origem, onde qualquer localização é representada pelas coordenadas X, Y e Z. Consulte a figura a seguir para obter um exemplo de um local de destino T expresso com coordenadas geocêntricas.

O raster de superfície é transformado do sistema de coordenadas de entrada em um sistema de coordenadas geocêntricas 3D.
O cálculo geodésico usa uma coordenada X, Y, Z que é calculada com base em suas coordenadas geodésicas (latitude φ, longitude λ, altura h). Se o sistema de coordenadas do raster de superfície de entrada for um sistema de coordenadas planas (PCS), o raster será primeiro reprojetado para um sistema de coordenadas geográficas (GCS) onde cada local tem uma coordenada geodésica. Em seguida, é transformado no sistema de coordenadas ECEF. A altura h (valor z) é a altura do elipsóide referenciada à superfície do elipsóide. Veja o gráfico de ilustração abaixo.

Para transformar em coordenadas ECEF a partir de uma coordenada geodésica (latitude φ, longitude λ, altura h), use as seguintes fórmulas:
X = (N(φ) + h) * cos(φ) * cos(λ)Y = (N(φ) + h) * cos(φ) * sin(λ)Z = (b2 / a2 * N(φ) + h) * sin(φ)- Onde:
N(φ) = a2 / √( a2 * cos(φ)2 + b2 * sin(φ)2)φ = latitude
λ = longitude
h = altura do elipsóide
a = eixo maior do elipsóide
b = eixo menor do elipsóide
A altura do elipsóide h está em metros nas fórmulas acima. Se a unidade z do raster de entrada for especificada em qualquer outra unidade, ela será transformada internamente em metros.
Leitura recomendada
Para uma maior compreensão dos métodos da análise de superfície e suas aplicações, consulte as referências abaixo. Além disso, Hengl e Reuter (2008) e Wilson (2018) fornecem uma catalogação abrangente dessas e de muitas outras técnicas de análise de terreno e suas aplicações. Minár et al (2020) fornece um resumo abrangente e uma comparação de trabalhos anteriores sobre a curvatura da superfície terrestre, com clareza e definição de muitos tipos de curvatura.
Referências
B. Hofmann-Wellenhof, H. Lichtenegger e J. Collins, 2001. GPS - teoria e prática. Seção 10.2.1. p. 282.
Burrough, P. A., e McDonell, R. A., 1998. Princípios dos Sistemas de Informações Geográficas (Oxford University Press, New York), 190 pp.
Crane K., 2018. Geometria Diferencial Discreta: Uma Introdução Aplicada. Avisos da AMS, Comunicação.. https://www.cs.cmu.edu/~kmcrane/Projects/DDG/paper.pdf
David Eberly 1999. Ajuste de Mínimos Quadrados de Dados (Geometric Tools, LLC), pp. 3.
E.J.Krakiwsky, e D.E.Wells, 1971. Sistemas de Coordenadas em Geodésia (GEODESY AND GEOMATICS ENGINEERING, UNB), LECTURE NOTES, No16, 1971, pp. 18-38
Hengl T. e Reuter H. 2008. Conceitos de Geomorfometria, Software, Aplicações. Elsevier.
James D.E., M.D. Tomer, S.A. Porter. 2014. Segmentação de relevo transescalar a partir de modelos digitais de elevação de alta resolução. Poster apresentado na: ESRI Annual Users Conference; Julho de 2014; San Diego, CA.
Lancaster, P. and Šalkauskas, K. Ajuste de Curva e Superfície: Uma Introdução. Londres: Academic Press, 1986.
Marcin Ligas, e Piotr Banasik, 2011. Conversão entre coordenadas Cartesianas e geodésicas em um elipsóide rotacional resolvendo um sistema de equações não lineares (GEODÉSIA E CARTOGRAFIA), Vol. 60, No 2, 2011, pp. 145-159
Minár, J., Evans, I. S., & Jenčo, M. (2020). Um sistema abrangente de definições de curvaturas (topográficas) da superfície terrestre, com implicações para sua aplicação em modelagem e previsão de geociências. Earth-Science Reviews, 103414. https://doi.org/10.1016/j.earscirev.2020.103414
Wilson J.P e Gallant, J.C. (Eds.) 2000. Análise de Terreno: Princípios e Aplicações. John Wiley & Sons, Inc.
Wilson J.P 2018. Aplicação Ambiental da Modelagem Digital de Terreno. John-Blackwell, Inc.
Zevenbergen, L. W., e C. R. Thorne. 1987. Análise Quantitativa de Topografia da Superfície Terrestre. Processos da Superfície Terrestre e Formas de Relevo 12: 47-56.