Summarize Within

Available in big data analytics.

The Summarize Within tool calculates statistics in areas where an input layer is within or overlaps a boundary layer. The area being summarized can be an area layer or a hexagonal or square bin.

Workflow diagram

Examples

The following are example uses of the Summarize Within tool:

• A cable provider is starting a pilot program that provides low-cost internet access to low-income community college students. Using Summarize Within by bins can be used to determine the number of low-income students within square bins of a defined size so the cable provider can determine an appropriate region for its pilot program.
• To complete routine maintenance projects efficiently, the city uses the Summarize Within tool to count the street lights and to sum the miles of bike lanes within each maintenance assessment district. It can then estimate the material and staff needed to complete the work in each district.

Usage notes

Keep the following in mind when working with the Summarize Within tool:

• The input layer to be summarized can be a point, line, or polygon layer.
• The output layer is always a polygon area or bin layer, and only the area or bin features where summarized features occur are returned.
• You can think of summarize within as taking two layers, the area features and the input summary features, and stacking them on top of each other. After stacking these layers, you view down through the stack and count the number of input summary features that fall within the areas. In addition to the number of features, you can also calculate simple statistics about the attributes of the input summary features, such as sum, mean, minimum, maximum, and so on.
• You can use the Summarize Within tool to calculate standard statistics and geographically weighted statistics. Standard statistics summarize the statistical values without weighting. Weighted statistics calculate values using the geographically weighted values of the proportion of lines within a polygon, or proportion of polygons within a polygon. Weighted statistics do not apply to points within polygons.

How the Summarize Within tool works

The following describe how the Summarize Within tool works.

Equations

For summarized line and area features, weighted statistics incorporate Summary Area weights. None of the statistics for point features are weighted. The following table shows the equations used to calculate variance, the weighted mean, and the weighted standard deviation.

Statistic	Equation	Variables	Features
Variance		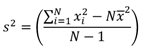	Points
Weighted Mean		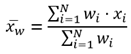Weights are calculated as the percentage of the feature within the summary area.	Lines and Areas
Weighted Standard Deviation		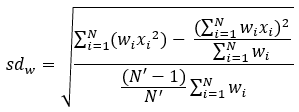Weights are calculated as the percentage of the feature within the summary area.	Lines and Areas

Points

Point layers are summarized using only the point features that fall within the Summary Area. Weighted statistics cannot be applied when summarizing points.

The figure and table below explain the statistical calculations of a point Summarized Layer within hypothetical areas. The Population field was used to calculate the statistics (Count, Sum, Minimum, Maximum, Range, Mean, Standard Deviation, and Variance) for the layer.

Point layers are summarized using only points located within the area layer. An example attribute table displays values to be used in hypothetical statistic calculations.

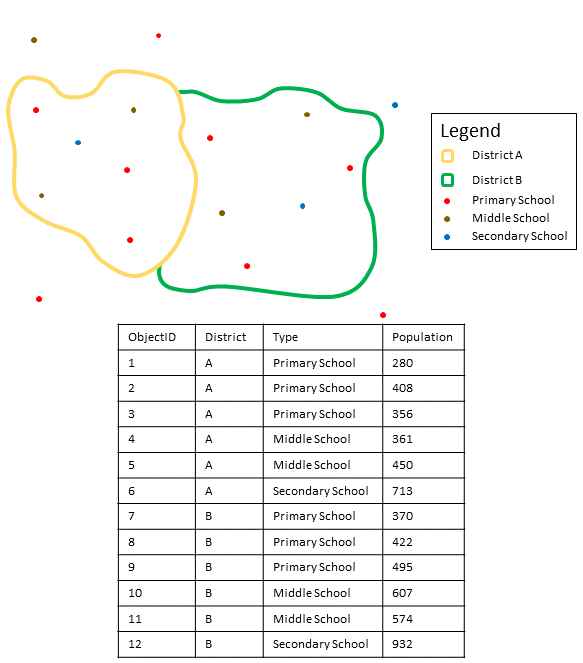
Numeric statistic	Results District A
Count	Count of: [280, 408, 356, 361, 450, 713] = 6
Sum	280 + 408 + 356 + 361 + 450 + 713 = 2,568
Minimum	Minimum of: [280, 408, 356, 361, 450, 713] = 280
Maximum	Maximum of: [280, 408, 356, 361, 450, 713] = 713
Range	713 - 280 = 433
Mean	2568/6 = 428
Variance	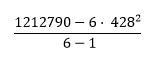= 22737.2
Standard Deviation	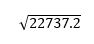= 150.7886

String statistic	Results District A
Count	= 6
Any	= Secondary School

Note:

The count statistic (for strings and numeric fields) counts the number of nonnull values. For example, the count of [0, 1, 10, 5, null, 6] is 5. The count of [Primary, Primary, Secondary, null] is 3.

A real-life scenario in which this analysis could be used is in determining the total number of students in each school district. Each point represents a school. The Type field gives the type of school (elementary, middle school, or secondary) and a student population field gives the number of students enrolled at each school. The calculations and results are given for District A in the table above. From the results, you can see that District A has 2,568 students. When running the Summarize Within tool, the results would also be given for District B.

Lines

For weighted statistics, line layers are summarized using only the proportions of line features that are within the Summary Area. Standard (non-weighted) statistics summarize any line intersecting the Summary Area. When summarizing lines using weighted statistics, use counts and amounts (rather than rates or indices) so proportional calculations make logical sense in your analysis.

The figure and table below explain the statistical calculations of a line Summarized Layer within a hypothetical Summary Area. The Volume field was used to calculate the statistics (Count, Sum, Minimum, Maximum, Range, Mean, Standard Deviation, and Variance) for the layer. The standard statistics are calculated using lines that intersect the boundary and the weighted statistics are calculated using the proportion of the lines that are within the Summary Area.

Line layers are summarized using standard statistics and weighted statistics.

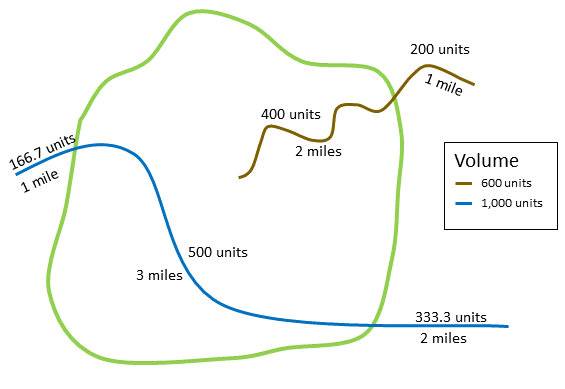
Numeric statistics	Standard statistics	Weighted statistics
Calculating Weights	Not applicable	Weight of the brown line (value = 600): 2/3 = .6667 Weight of the blue line (value = 1000): 3/6 = .5
Count	Count of: [1000, 600] = 2	Count of: 1 x (3/6) + 1 x (2/3) = 1.1667
Sum	1000 + 600 = 1600	1000 x (3/6) + 600 x (2/3) = 900
Minimum	Minimum of: [1000, 600] = 600	Minimum of: [1000 x (3/6), 600 x (2/3)] [500, 400] = 400
Maximum	Maximum of: [1000, 600] = 1000	Maximum of: [1000 x (3/6), 600 x (2/3)] [500, 400] = 500
Range	1000 - 600 = 600	500 - 400 = 100
Mean	(1000 + 600)/2 = 800	(1000 x (3/6) + 600 x (2/3))/(3/6 + 2/3) (500 + 400)/(7/6) = 771.4286
Variance	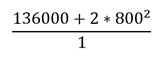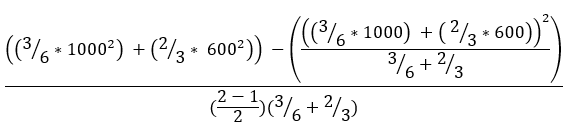= 80000	= 1268571.4286
Standard Deviation	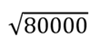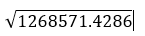= 282.8427	= 1126.3088

A real-life scenario in which this analysis could be used is in determining the total volume of water in rivers within the boundaries of a state park. Each line represents a river that is partially located inside the park. From the results, you can see that there are 5 miles of rivers within the park and the total volume is 900 units.

Areas

Area layers are summarized using only the proportions of the area features that are within the input boundary. When summarizing areas, use fields with absolute numbers so proportional calculations make logical sense in the analysis.

Weighted statistics for summarized area layers are based on the proportions of the Summary Area features that are within the Summarized Layer. When summarizing areas, use counts or amounts (rather than rates or indices) so proportional calculations make logical sense in your analysis.

The figure and table below explain the statistical calculations of an area layer within a hypothetical Summary Area. The population field was used to calculate the statistics (Count, Sum, Minimum, Maximum, Range, Mean, Standard Deviation, and Variance) for the layer. The standard statistics are calculated using areas that intersect the Summary Area, and the weighted statistics are calculated using a proportional weight based on the portion of summary areas contained within each Summarized Layer.

Summary statistics are computed for areas in the summarized layer that intersect the summary areas. Weights are based on the proportion of the summary areas that overlap the summarized layer features.

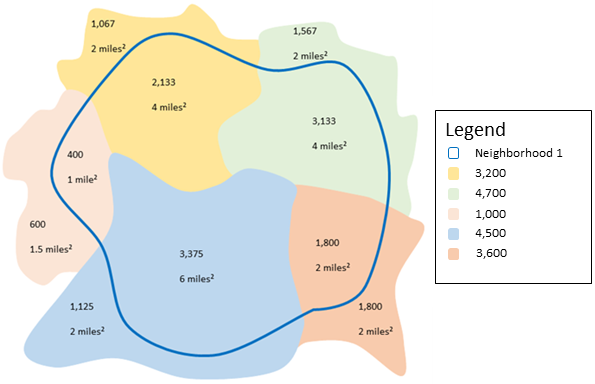
Numeric statistics	Standard statistics: Results Neighborhood 1	Weighted statistics: Results Neighborhood 1
Calculating Weights		Weight of the yellow area (value = 3200): 4/(2+4) = 4/6 Weight of the green area (value = 4700): 4/(2+4) = 2/3 Weight of the pink area (value = 1000): 1/(1+1.5) = 2/5 Weight of the blue area (value = 4500): 6/(2+6) = 3/4 Weight of the orange area (value = 3600): 2/(2+2) = 1/2
Count	Count of: [3200, 4700, 1000, 4500, 3600] = 5	Count of: (2/3)+(2/3)+ (2/5)+(3/4)+ (1/2) = 2.98
Sum	3200 + 4700 + 1000 + 4500 + 3600 = 17000	(3/4) x 3200 +(2/3) x 4700 + (2/5) x 1000 +(3/4) x 4500 + (1/2) x 3600 = 10841.67
Minimum	Minimum of: [3200, 4700, 1000, 4500, 3600] = 1000	Minimum of: [(2/3) x 3200, (2/3) x 4700, (2/5) x 1000, (3/4) x 4500, (1/2) x 3600] [2133.33, 3133.33, 400, 3375, 1800] = 400
Maximum	Maximum of: 3200, 4700, 1000, 4500, 3600] = 4700	Maximum of: [2133.33, 3133.33, 400, 3375, 1800] = 3375
Range	4700 - 1000 = 3700	3375 - 400 = 2,975
Mean	(17000)/5 = 3400	(10841.67)/[2.9833] = 3634.12
Variance	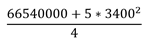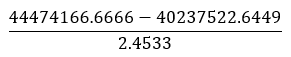= 2185000	= 1727137.5112
Standard Deviation	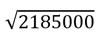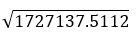= 1478.175	= 1314.2060

Parameters

The following are the parameters for the Summarize Within tool:

Parameter	Description	Data type
Input Layer	The point, line, or polygon features that will be summarized within area features.	Features
Bin Type	The bin shape that will be used to create the regular bins. Options are Square and Hexagon. If a polygon source is connected to the join port of this tool, this parameter will no longer appear or be required.	String
Bin Size	The distance interval that represents the bin size into which the input points will be aggregated. For square bins, the bin size represents the height of a square. This is the default. For hexagonal bins, the bin size represents the height between two parallel sides. If a polygon source is connected to the join port of this tool, this parameter will no longer appear or be required.	String
Summarize Shapes	Specifies whether shape information will be summarized as part of the analysis (length of lines or area of polygons). If the input summary features are points, there is no shape information to summarize. Only the count of points within each area feature is added.	Boolean
Shape Units	The unit in which to calculate shape summary attributes. If the input summary features are lines, specify a linear unit. If the input summary features are polygons, specify an areal unit.	String
Summary Fields	The statistics that will be calculated for specified fields. Different statistics are available depending on whether the specified field is a string, numeric, or date field. Any—A sample string from a field of type string. Count—Calculates the number of nonnull values. It can be used on numeric fields or strings. The count of [null, 0, 2] is 2. Count Distinct—Calculates the number of distinct, nonnull values. It can be used on numeric fields or strings. The count distinct result of [null, 4, 3, 4] is 2. Sum—The sum of numeric values in a field. The sum of [null, 1, 3] is 4. Sum of Squares—The sum, over all observations, of the squared differences of each observation from the overall mean. The sum of squares of [null, 2.2, 3.1, 4.7] is 3.206. Min—The minimum value of a numeric field. The minimum of [0, 2, null] is 0. Max—The maximum value of a numeric field. The maximum value of [0, 2, null] is 2. Mean—The mean of numeric values. The mean of [0, 2, null] is 1. Range—The range of a numeric field. This is calculated as the minimum value subtracted from the maximum value. The range of [0, null, 1] is 1. The range of [null, 4] is 0. Variance—The variance of a numeric field in a track. The variance of [1] is null. The variance of [null, 1, 1, 1] is 1. Standard Deviation—The standard deviation of a numeric field. The standard deviation of [1] is null. The standard deviation of [null, 1, 1, 1] is 1.	String
Weighted Statistics	The geographically weighted statistics that will be calculated for specified fields. Weighted statistics calculate values using the geographically weighted values of the proportion of lines within a polygon, or proportion of polygons within a polygon. Weighted statistics do not apply to points within polygons. Different statistics are available depending on whether the specified field is a string, numeric, or date field. Count—Calculates the number of nonnull values. It can be used on numeric fields or strings. The count of [null, 0, 2] is 2. Sum—The sum of numeric values in a field. The sum of [null, 1, 3] is 4. Min—The minimum value of a numeric field. The minimum of [0, 2, null] is 0. Max—The maximum value of a numeric field. The maximum value of [0, 2, null] is 2. Mean—The mean of numeric values. The mean of [0, 2, null] is 1. Range—The range of a numeric field. This is calculated as the minimum value subtracted from the maximum value. The range of [0, null, 1] is 1. The range of [null, 4] is 0.	String

Output layer

The output layer will contain the following fields in place of the original fields. If you configured summary fields, those fields will also be calculated for the output layer.

Field name	Description	Field type
COUNT	The number of features from the input layer that were summarized into this polygon bin.	Float64
sum_length_<units>	If the input layer is a polyline feature, and the Summarize Shapes parameter is set to Yes, the output will generate this field that reports the total length of polyline features within each bin, in the units specified by the Shape Units parameter.	Float64
sum_area_<units>	If the input layer is a polygon feature, and the Summarize Shapes parameter is set to Yes, the output will generate this field that reports the total area of polygon features within each bin, in the units specified by the Shape Units parameter.	Float64

Considerations and limitations

Lines and areas are summarized using proportions; therefore, it is best to summarize absolute data (such as population) rather than relative data (such as average income) when lines or areas are being summarized.