A zonal statistics operation calculates statistics on cell values of a raster (a value raster) within the zones defined by another dataset. The tools that calculate statistics by zones are Zonal Statistics and Zonal Statistics as Table.
The Zonal Statistics tool calculates one statistic at a time and creates a raster output. This value becomes the cell value of the raster output for the cells corresponding to that zone. If a zone feature contains overlapping zones, the statistic is computed for only one zone because a cell in the output raster can represent only one value.
The Zonal Statistics as Table tool calculates one or multiple statistics using predefined subsets or all statistics and creates a table output. As with Zonal Statistics, the resulting statistic is a single value for each zone. There is one record per zone in the output table and statistics values are reported in predefined fields. If the zone input is a feature and it contains overlapping zones, statistics are computed for all zones, and the output is reported in individual records for each zone.
The input zone layer defines the shape, values, and locations of the zones, which can be either raster or feature. During the zonal operation, feature data is first converted to a raster. In raster data, a zone is all the cells that have the same value, whether they are contiguous or not. Each zone must have a unique identity and if it is a raster, it must have an integer data type. Any integer or string field of unique values in the zone input can be specified to define the zones.
The input value raster contains the values used in calculating the output statistic for each zone. It can be of integer or float data type.
In the following illustration, the mean of the value input is identified for each zone:
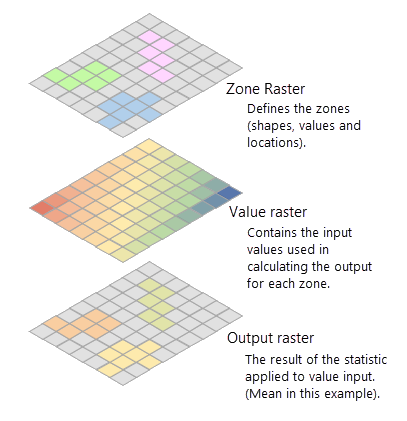
How cells in a value raster are identified for a raster zone
To calculate a statistic, the tool first extracts cell values from the value raster for all cells that fall within each zone. This identification of cells in a value raster within a zone is done by overlaying zones on the value raster. When the zone and value inputs are both rasters of the same cell size and the cells are aligned, the cell values of the value raster that overlays that of the zones are extracted and statistics are calculated.
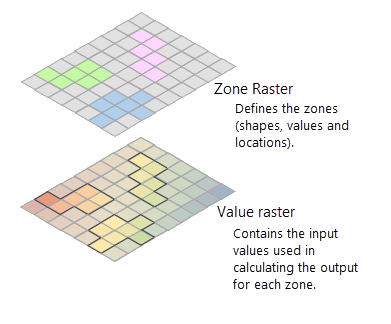
When either the cell size or alignment of the zone raster is different from that of the value raster, the cells between the zone and value rasters cannot be overlaid perfectly on each other. The tool then adjusts one or both rasters to achieve the perfect overlay of cells. This adjustment is done following some simple rules. When the cell size of the zone raster and the value raster is different, the output cell size and the snap raster is determined by the value raster internally. If the cell size is the same but the cells are not aligned, the value raster will be used as the snap raster internally. Either of these cases will cause an internal resampling before the zonal operation is performed.
How cells in a value raster are identified for a feature zone
A zonal operation is fundamentally a raster analysis performed on two rasters in which one is the zone and the other is the value. If the zones are defined by features, an internal feature-to-raster conversion will occur. The internal conversion for a polygon zone uses the cell center method in the Convert Feature to Raster tool to rasterize the input using the cell size and the snap raster of the value raster.This can lead to an unexpected result of missing zones in the output when none of the cell centers of the rasterization grid fall within the feature zone. This can occur with zones that are smaller than the area of a cell of the internal zone raster as well as with larger zones.
In the example below, figure (1) represents the input feature zone, the input value raster, and its cell center. The input features have three zones (yellow shapes) in which the following are true:
- zone1 is larger than an individual cell.
- zone2 and zone3 are smaller than a cell.
- A cell center falls outside zone2 but within zone3.
During the zone rasterization process in figure (2), since no cell centers fall within zone1 and zone2, only zone3 is rasterized, and the other two zones essentially disappear.
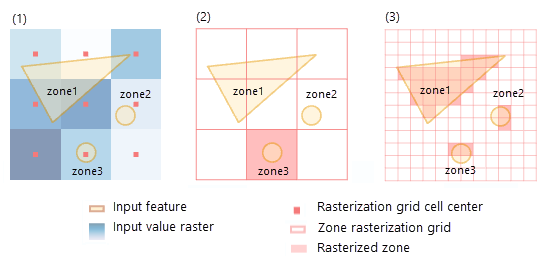
To avoid zones disappearing from the output, ensure that each zone contains one or more cell centers from the value raster. One way to do this is to create more cell centers by specifying a smaller cell size in the environment. By default, the analysis cell size is that of the value raster. However, if you specify a cell size in the analysis environment that is smaller than that of the value raster, you will enable more zones to be captured, as figure (3) above demonstrates. Keep in mind that specifying a smaller cell size will generate a larger output raster. The higher resolution output will not necessarily be as high quality a result as it seems, since the additional detail does not actually exist in the input value raster.
Once a feature zone is converted to a raster zone using the same cell size and cell alignment of the value raster, the extraction of cells from a value raster within a zone is done by overlaying the zones on the value raster.
Calculate arithmetic and circular statistics
Calculating a mean by summing all the cell values, then dividing by the number of cells may work with data such as elevation. However, if the data represents cyclic quantities such as aspect (compass direction of 0 degrees to 360 degrees) or hours of a day (0 to 24 hours), calculating the arithmetic mean will produce incorrect output, because the minimum value and the maximum value represent the same quantity. For this kind of data, you should calculate circular statistics.
For example, if you are calculating the mean of two cell values, 0 degrees and 360 degrees, the arithmetic mean will be 180 degrees. This is incorrect because 0 degrees and 360 degrees represent the same compass direction. The correct statistics can be obtained by calculating circular mean, which will be 0 degrees.
You can specify circular statistics calculation by checking the Calculate Circular Statistics (circular_calculation = "CIRCULAR" in Python) parameter. When calculating circular statistics, pay attention to the lowest and highest values for representing the cyclic data. The lowest value is assumed to be 0. The highest value can be specified as the Circular Wrap Value (circular_wrap_value in Python) parameter. The default for this parameter is 360.
Depending on the type of data, select the type of statistics calculation, and an appropriate circular wrap value for circular statistics, to get the correct output. The following circular statistics options are available: Mean, Majority, Minority, Standard deviation, and Variety.
Calculate zonal statistics with multidimensional rasters
Multidimensional raster data represents data at multiple times and multiple depths or heights. This type of data is commonly used in atmospheric, oceanographic, and earth sciences and is observed by monitoring platforms, captured by satellites, or generated from numerical simulation models where data is processed, aggregated, or interpolated using various statistical techniques.
The Zonal Statistics and Zonal Statistics as Table tools support multidimensional zone and value raster data as input. Zonal statistics are calculated for all slices of a multidimensional raster when the Process as Multidimensional parameter is checked (ALL_SLICES in the process_as_multidimensional parameter in Python). If the Process as Multidimensional parameter is unchecked (CURRENT_SLICES in Python), only the current slice will be processed.
Examples of zonal statistics analysis on multidimensional data include the following:
- A meteorologist wants to gain insight on hurricane movement and the precipitation distribution along the hurricane track for a given period. Using multidimensional processing in the Zonal Statistics tool, the meteorologist can find the average precipitation for each time slice for the hurricane zones that changed over time.
- An ecologist wants to determine the distribution of extreme events from a maximum daily rainfall data for the last 30 years for a particular river basin. The Zonal Statistics as Table tool with the percentile statistic type for a list of percentile values can be used to find the distribution of the maximum daily rainfall data for the time series data when processing as multidimensional.
Zonal statistics multidimensional output
When you specify that the Zonal Statistics tool is to process the input as multidimensional, the tool will create a multidimensional raster output. The zonal operation occurs slice by slice between the slices of the zone raster and the slices of the current variable from the value raster. The calculated statistic values are stored in a multidimensional variable whose name is created by combining the variable name from the value raster and the statistic being calculated. The number of dimensions of the output variable and the number of slices depend of the specific nature of the zone and value raster inputs.
For the Zonal Statistics as Table tool, when you specify that the data is to be processed as multidimensional, it will generate a flat table output with the statistics computed for all zones and slices. This table will include additional fields to indicate the variable name, the dimension names and their values, and the statistics that are computed for each zone.
Since the multidimensional processing occurs slice by slice between the zone and value rasters, the number of slices in the output multidimensional raster from the Zonal Statistics tool and the number of records in the output table from the Zonal Statistics as Table tool will depend of the type of the input rasters and the number of slices in them. The following subsections describe examples.
Multidimensional zone and value rasters with the same dimensions
Finding the maximum salinity at various depths of the ocean for various temperature ranges at a corresponding depth will require performing zonal statistics with a multidimensional zone representing temperature zones and a multidimensional value raster representing salinity. The zonal operation will be performed for each zone slice with the corresponding slice from the value raster. The output multidimensional raster will have the same number of slices as the value raster.
In the illustration below, the variables in both the zone and the value rasters have the same three dimensions, x, y, and d and the same number of slices at dimension values d0, d1, and d2. The variable in the output multidimensional raster will also have the same three dimensions, x, y, and d and the same number of slices at dimension values d0, d1, and d2.
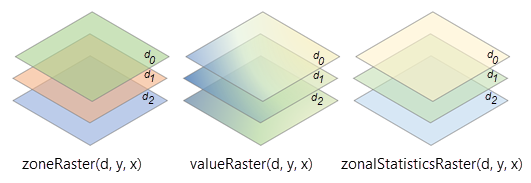
The total number of records in the Zonal Statistics as Table tool output is determined by adding the number of zones in each slice. If the number of zones at depths d0, d1, and d2 are 5, 4, and 3, respectively, the total number of records will be 12 (5 + 4 + 3 = 12).
Multidimensional zone and value rasters with different dimensions
A suitable location and time window to deploy assets such as remotely operated vehicles (ROVs) can be determined by performing zonal statistics with a multidimensional zone representing potential locations for ROVs at different times, and multidimensional value raster such as the Hybrid Coordinate Ocean Model (HYCOM) model output representing ocean current at different depths and times.
The zonal operation will be performed for each slice from the zone raster with each slice from the value raster. The number of slices in the output multidimensional raster is determined by multiplying the number of slices in the zone raster by the number of slices in the value raster.
In the illustration below, the variable in the zone raster has three dimensions, x, y, and d, and three slices at dimension values, d0, d1 and d2. The variable in the value raster has three dimensions, x, y, and t, and two slices at dimension values, t0 and t1. The variable in the output multidimensional raster will also have four dimensions: x, y, d, and t.
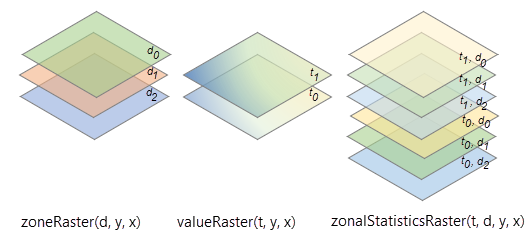
The total number of slices in the Zonal Statistics tool output is determined by multiplying the number of depths in the zone raster by the number of time steps in the value raster, which in this case, will be 6 (3 depths x 2 times = 6). The total number of records in the Zonal Statistics as Table tool output is determined by multiplying the number of zones in each slice. If the number of zones is 5, the total number of records in this case is 30 (5 zones x 3 depth x 2 time = 30).
Multidimensional value raster only
Finding the maximum temperature in each county for each day of the year will require performing zonal statics with a multidimensional value raster representing daily temperature, and a zone raster representing counties. The zonal operation will be performed for each slice from the value raster using the same zone raster. The output multidimensional raster will have the same number of slices as the value raster.
In the illustration below, the variables in the value raster has three dimensions, x, y, and t, and three slices at dimension values, t0, t1, and t2. The variable in the output multidimensional raster will also have the same three dimensions, x, y, and t, and the same number of slices at dimension values, t0, t1, and t2.
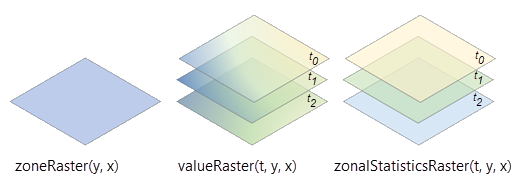
The total number of records in the Zonal Statistics as Table tool output is determined by multiplying the number of zones and the number of slices in the value raster. If the number of zones is 5, the total number of records will be 15 (5 x 3 =15).
Multidimensional zone raster only
Finding the mean of decadal maximum precipitation within each time-varying floodplain zone category that changes over time for ecological landscape planning will require performing zonal statics with a multidimensional zone raster representing floodplain zones and a value raster representing decadal maximum precipitation. The zonal operation will be performed for each slice from the zone raster using the same value raster. The output multidimensional raster will have the same number of slices as the zone raster.
In the illustration below, the variables in the zone raster have three dimensions, x, y, and t, and three slices at dimension values, t0, t1, and t2. The variable in the output multidimensional raster will also have the same three dimensions, x, y, and t, and the same number of slices at dimension values, t0, t1, and t2.
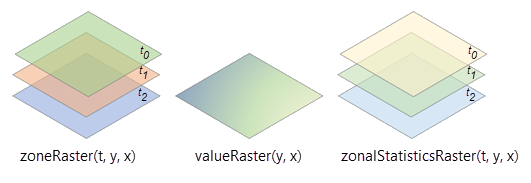
The total number of records in the Zonal Statistics as Table tool output is determined by multiplying the number of zones by the number of slices in the zone raster. If the number of zones is 5, the total number of records will be 15 (5 x 3 =15).
Statistics
The available statistics types to compute zonal statistics are listed below with additional details and a graphic illustration showing the results for each option on an example input.
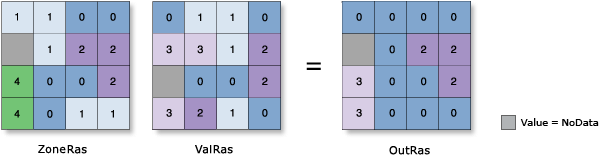
Majority
- The most frequently occurring value in each zone is assigned to all cells in that zone.
- When there is a tie for the majority value in a zone, the output for all cell locations in the zone is assigned the lowest of the tied values.
Example:
Majority count
- The count of the most frequently occurring value in each zone is assigned to all cells in that zone.
Majority percentage
- The percentage of the count of the most frequently occurring value in each zone is assigned to all cells in that zone.
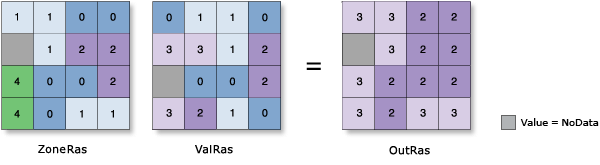
Maximum
- The highest value in each zone is assigned to all cells in that zone.
Example:
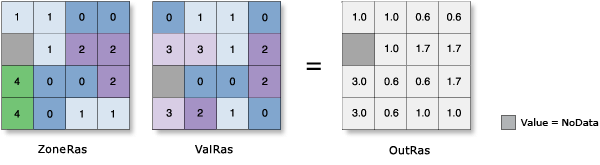
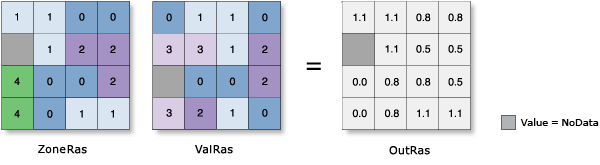
Mean
- The average of the values in each zone is assigned to all output cells in that zone.
- The formula for arithmetic mean is as follows:

where:
- x̄ = mean
- xi = observed values
- N = number of observations
- The formula for circular mean is as follows:

where:
- x̄ = circular mean
- xi = observed values
- N = number of observations
In the degenerate case in which both Σsin xi and Σcos xi are equal to zero, the special value -1 is used, indicating that the circular mean is not well defined.
Example:
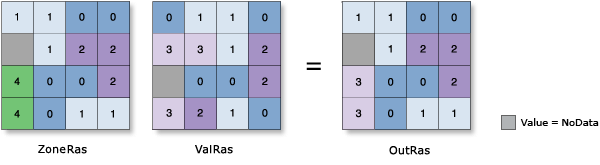
Median
- The median of the values in each zone is assigned to all output cells in that zone.
- The statistics type values are computed using method Q1 from Hyndman and Fan (1996). When two sorted values are equally close to the target median value, the smaller of the two values is used.
- To calculate the median, all the cells in a zone are ranked. If there are n cells in the zone and n is odd, the middle ((n+1)/2) value is written to each cell in the zone. If there is an even number of cells, the (n/2) value is output.
Example:
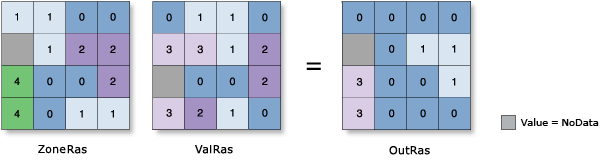
Minimum
- The lowest value in each zone is assigned to all cells in that zone.
Example:
Minority
- The least frequently occurring value in each zone is assigned to all cells in that zone.
- When there is a tie for the minority value in a zone, the output for all cell locations in the zone is assigned the lowest of the tied values.
Example:
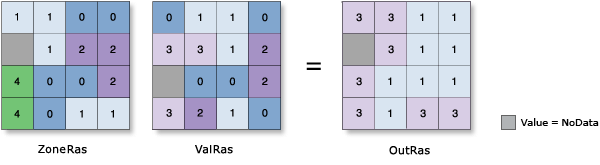
Minority count
- The count of the least frequently occurring value in each zone is assigned to all cells in that zone.
Minority percentage
- The percentage of the count of the least frequently occurring value in each zone is assigned to all cells in that zone.
Percentile
- The percentile of the values in each zone is assigned to all output cells in that zone.
- This statistics type value is computed using method Q1 from Hyndman and Fan (1996). When two sorted values are equally close to the target median value, the smaller of the two values is used.
- To calculate the percentile, all the cells in a value raster are ranked using the following formula: R = P/100 x (n - 1) +1, where P is the desired percentile, and n is the number of cells.
Example: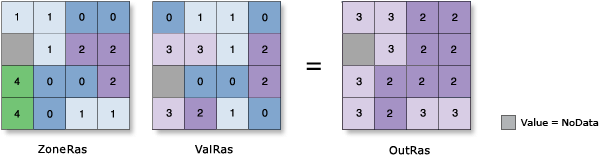
Range
- The difference between the maximum and minimum values in each zone is assigned to all cells in that zone.
- The range is defined as follows:
Zonal Range = Zonal Maximum – Zonal Minimum
Example: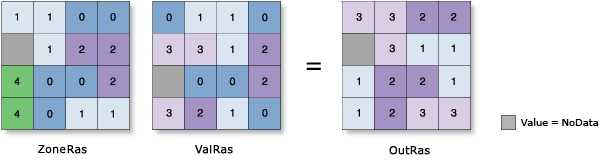
Standard deviation
- The standard deviation of the values in each zone is assigned to all cells in that zone.
- The formula for arithmetic standard deviation is as follows:

where:
- σ = standard deviation
- xi = observed values
- x̄ = mean
- N = number of observations
Note:
The standard deviation is calculated on the entire population (the N method), not estimated based on a sample (the N-1 method). For comparison, the calculation for standard deviation is equivalent to the STDEVP method, not the STDEV method, in Microsoft Excel.
- The formula for circular standard deviation is as follows:

where:
- σ = Circular standard deviation
- R̄ = Mean resultant length of

In a sample of n angles in degrees, angles of a1, a2, …, an are summarized, and each angle is represented by a unit vector,
 , that points in the direction of the corresponding observation.
, that points in the direction of the corresponding observation.
Example:
Sum
- The sum of all the cell values in each zone is assigned to all cells in that zone.
- The data type of the output raster is floating point. This is because the value for the sum tends to be quite large, and it may not be possible to represent it with an integer value.
For example, for a zone that is 2,500 rows and columns of cells in size, and the value of each cell is 1,000, the sum for that zone would be 2,500 x 2,500 x 1,000 = 6.25 billion. If an integer output is required and the range is within ± 2.147 billion, you can apply the Int tool.
Example: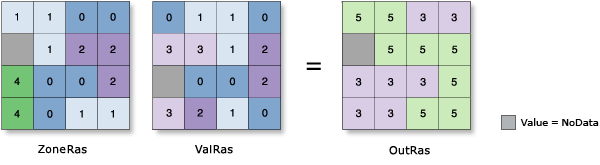
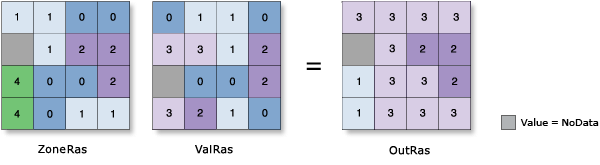
Variety
- The number of unique values in each zone is assigned to all cells in that zone
Example:
Output data type
The output data type (integer or float) is determined by both the zonal calculation being performed and the input value raster type. The following table identifies the expected data types of the output raster:
| Statistic | Value input type | Output |
|---|---|---|
Majority | Integer* | Integer |
Majority count | Integer* | Integer |
Majority percentage | Integer* | Float |
Maximum | Integer, Float | Same as Value |
Mean | Integer, Float | Float |
Median | Integer, Float | Integer |
Minimum | Integer, Float | Same as Value |
Minority | Integer* | Integer |
Minority count | Integer* | Integer |
Minority percentage | Integer* | Float |
Percentile | Integer, Float | Integer |
Range | Integer, Float | Same as Value |
Standard deviation | Integer, Float | Float |
Sum | Integer, Float | Float |
Variety | Integer* | Integer |
Note:
* Only integer is supported.
If any cell location in the Zone dataset is NoData, that location will be assigned NoData in the output.
References
Rob J. Hyndman and Yanan Fan (1996) "Sample Quantiles in Statistical Packages" The American Statistician, Vol. 50, No. 4 (Nov., 1996), pp. 361-365.