


Análise de link é uma técnica de análise que se concentra em conexões e relacionamentos em um conjunto de dados. A análise de link fornece a você a habilidade de calcular medidas de centralidade—isto é grau, intermediação, proximidade, e autovetores—e veja as conexões em um gráfico de link ou mapa de link.
Sobre análise de link
A análise de link utiliza uma rede de links e nós interconectados para identificar e analisar relacionamentos que não são facilmente vistos em dados brutos. Tipos comuns de redes incluem o seguinte:
- Redes sociais que mostram quem fala com quem
- Redes semânticas que ilustram tópicos relacionados entre si
- Redes de conflito indicando alianças de conexões entre jogadores
- Redes de companhias aéreas que indicam quais aeroportos têm voos de conexão
Exemplos
Um analista criminal está investigando uma rede criminosa. Dados de registros de celulares podem ser utilizados para determinar o relacionamento e a hierarquia entre os membros da rede.
Uma empresa de cartão de crédito está desenvolvendo um novo sistema para detectar roubo de cartão de crédito. O sistema utiliza os padrões conhecidos de transações para cada cliente, como a cidade, as lojas e os tipos de transações, para identificar anomalias e alertar o cliente sobre um potencial roubo.
Um analista de saúde pública está pesquisando a crise de opióides na América do Norte. O analista utiliza dados sobre prescrições e demografias para identificar novos padrões que estão surgindo à medida que a crise se espalha.
Como funciona a análise de link
A seguinte tabela fornece uma visão geral de terminologia na análise de link:
| Termo | Descrição | Exemplos |
|---|---|---|
Rede | Um conjunto de nós e links interconectados. | Uma rede social online, que utiliza uma rede de perfis e relacionamentos para conectar usuários. Redes de companhias aéreas, que utilizam uma rede de aeroportos e voos para transportar viajantes desde sua origem até seu destino. |
Nó | Um ponto ou vértice que representa um objeto, como uma pessoa, local, tipo de crime ou tweet. O nó também pode incluir propriedades associadas. | Os perfis em uma rede social. As propriedades associadas podem incluir o nome de usuário, cidade natal ou empregador. Os aeroportos em uma rede de companhias aéreas. Propriedades associadas podem incluir o nome do aeroporto. |
Vincular | Os relacionamentos ou conexões entre nós. O link também pode incluir propriedades associadas. | O relacionamento entre perfis na rede, como amigo, seguidor ou conexão. Propriedades associadas podem incluir o tamanho do relacionamento. Os voos entre aeroportos em uma rede de companhias aéreas. As propriedades associadas podem incluir o número de voos entre aeroportos. |
Centralidade
A centralidade é uma medida de importância para nós em uma rede.
A centralidade geral é utilizada para os seguintes propósitos:
- Avaliar a influência de um nó sobre outros nós na rede. Por exemplo, qual usuário alcançará o maior número de outros usuários ao compartilhar uma notícia ou uma oportunidade de emprego?
- Identificar os nós que são mais influenciados por outros nós. Por exemplo, qual aeroporto será mais afetado por voos cancelados devido a uma tempestade em outra região?
- Observar o fluxo ou propagação de algo em toda a rede, incluindo informações, objetos ou fenômenos. Por exemplo, como um pacote é movido do depósito para o endereço de entrega?
- Entender quais nós espalham os fenômenos pela rede com mais eficiência. Por exemplo, qual jornal ou canal deve ser contatado para que a história chegue ao maior número de pessoas?
- Localizar nós que podem bloquear ou impedir a propagação de fenômenos. Por exemplo, onde as clínicas de vacinação devem estar localizadas para impedir a propagação de um vírus?
Há quatro maneiras de medir a centralidade no Insights:centralidade de grau, centralidade de intermediação, centralidade de proximidade, e centralidade de autovetor.
Cálculos para intermediação, proximidade e centralidades de autovetores podem ser ponderados ou não ponderados.
Centralidade de grau
A centralidade de grau é baseada no número de conexões diretas de um nó. A centralidade de grau deve ser utilizada quando você deseja determinar quais nós têm a influência mais direta. Por exemplo, em uma rede social, os usuários com mais conexões tem um maior grau de centralidade.
A centralidade de grau do nó x é calculada utilizando a seguinte equação:
degCentrality(x)=deg(x)/(NodesTotal-1)Onde:
- Total de Nós = O número de nós na rede
- deg(x) = O número de nós conectados ao nó x
Se os links estiverem direcionados, o que significa que a informação flui entre os nós em apenas uma direção, a centralidade de grau poderá ser medida como um grau interno ou externo. No caso de uma rede social, o grau interno seria baseado no número de perfis que o usuário está seguindo, enquanto o grau externo seria baseado no número de seguidores do usuário.
A centralidade de grau interno é calculada utilizando a seguinte equação:
indegCentrality(x)=indeg(x)/(NodesTotal-1)Onde:
- Total de Nós = O número de nós na rede
- indeg(x) = O número de nós conectados ao nó x com fluxo direcionado para o nó x
A centralidade de grau externo é calculada utilizando a seguinte equação:
outdegCentrality(x)=outdeg(x)/(NodesTotal-1)Onde:
- Total de Nós = O número de nós na rede
- outdeg(x) = o número de nós conectados ao nó x com fluxo direcionado para longe do nó x
Para gráficos direcionados, o Insights dimensiona os nós por centralidade externa por padrão.
Centralidade de intermediação
A centralidade de intermediação é baseada na extensão que um nó faz parte do caminho mais curto entre outros nós. A centralidade de proximidade deve ser utilizada quando você deseja determinar quais nós são utilizados para conectar outros nós uns aos outros. Por exemplo, um usuário em uma rede social com conexões para vários grupos de amigos terá uma centralidade de intermediação maior do que os usuários com conexões em apenas um grupo.
A centralidade de intermediação do nó x é calculada utilizando a seguinte equação:
btwCentrality(x)=Σa,bϵNodes(pathsa,b(x)/pathsa,b)Onde:
- Nós = todos os nós na rede
- pathsa,b = O número do caminho mais curto entre todos os nós a e b
- pathsa,b(x) = O número de caminhos mais curtos entre os nós a e b que se conectam através do nó x
A equação da centralidade de intermediação acima não leva em conta o tamanho da rede, de modo que grandes redes tenderão a ter valores de centralidade de intermediação maiores do que as redes pequenas. Para permitir comparações entre redes de tamanhos diferentes, a equação da centralidade de intermediação deve ser normalizada por divisão pelo número de pares de nós no gráfico.
A seguinte equação é utilizada para normalizar um gráfico não direcionado:
1/2(NodesTotal-1)(NodesTotal-2)Onde:
- Total de Nós = O número de nós na rede
A seguinte equação é utilizada para normalizar um gráfico direcionado:
(NodesTotal-1)(NodesTotal-2)Onde:
- Total de Nós = O número de nós na rede
Centralidade de proximidade
A centralidade de proximidade é baseada na média da menor distância de caminho da rede entre os nós. A centralidade de proximidade deve ser utilizada quando você deseja determinar quais nós estão mais intimamente associados aos outros nós na rede. Por exemplo, um usuário com mais conexões na rede social terá uma centralidade de proximidade maior do que um usuário conectado por meio de outras pessoas (em outras palavras, um amigo de um amigo).
Anotação:
A distância entre os nós faz referência ao número de links que os separam, não à distância geográfica.
A centralidade de proximidade do nó x é calculada utilizando a seguinte equação:
closeCentrality(x)=(nodes(x,y)/(NodesTotal-1))*(nodes(x,y)/dist(x,y)Total)Onde:
- Total de Nós = O número de nós na rede
- Nodes(x,y) = O número de nós que estão conectados ao nó x
- dist(x,y)Total = A soma das distâncias do caminho mais curto do nó x até outros nós
Centralidade de autovetor
A centralidade de autovetor é baseada em nós importantes que estão sendo conectados a outros nós importantes. A centralidade de autovetor deve ser utilizada quando você deseja determinar quais nós são parte de um grupo de influência. Por exemplo, um usuário em uma rede social com muitas conexões para outros usuários com muitas conexões terá uma centralidade de autovetor maior do que um usuário com poucas conexões ou que esteja conectado a outros usuários com poucas conexões.
A centralidade de autovetor do nó x é calculada utilizando iteração de potência para encontrar o maior autovetor utilizando a seguinte equação:
Ax=λxOnde:
- λ = O autovalor
- x = O autovetor
- A = A matriz que descreve a transformação linear
Peso do segmento
Cálculos para proximidade, intermediação e centralidades de autovetores podem ser ponderados ou não ponderados. Um cálculo de centralidade não ponderado define as extremidades com um peso uniforme com um valor de 1, enquanto um cálculo ponderado usa valores de campo para atribuir um valor a cada extremidade.
Anotação:
Pesos indefinidos recebem um valor de 1. É uma prática recomendada atribuir um campo sem valores nulos ou ausentes para o peso da extremidade.
Para a centralidade do autovetor, os pesos são usados para determinar a força da conexão entre os nós. Como a centralidade do autovetor mede a importância dos nós dentro da rede, valores de peso mais altos correspondem a valores mais altos para seus nós de conexão.
Para as centralidades de proximidade e intermediação, os valores de peso significam a distância entre os nós. Pesos de extremidade mais altos significam uma distância maior entre os nós e reduzem a probabilidade de a extremidade ser usada no caminho mais curto. Se um número maior no campo de peso desejado indicar maior importância (por exemplo, o número de mensagens enviadas entre membros em uma rede social indica como os membros estão conectados), um novo campo deve ser calculado com valores inversos. Use a seguinte equação para calcular um campo de valores inversos:
weight=ABS(field-MAX(field))+IF(MIN(field)<0, ABS(MIN(field)), MIN(field))Para um cálculo de proximidade ou intermediação não ponderado, o caminho mais curto é o caminho que usa o menor número de links. O exemplo abaixo mostra uma rede com quatro nós (A, B, C e D) e pesos uniformes. Há dois caminhos que unem o nó A ao nó D: A-B-D ou A-B-C-D. Como A-B-D tem menos links, é o caminho mais curto.

Um cálculo ponderado aplica pesos a cada extremidade com base nos valores do campo. As centralidades ponderadas de proximidade e intermediação usam o algoritmo de Bellman-Ford para encontrar os caminhos mais curtos entre os nós.
O exemplo abaixo mostra uma rede com quatro nós e extremidades ponderadas. O caminho A-B-D tem um valor de 15 e o caminho A-B-C-D tem um valor de 9. Como A-B-C-D tem o menor valor de borda, é o caminho mais curto.
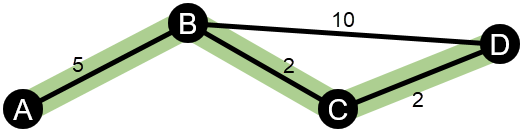
Os cálculos de proximidade ponderada e centralidade de intermediação não suportam ciclos de peso negativo. Se for detectado um ciclo de peso negativo, todos os valores de centralidade são definidos como 0. Um ciclo de peso negativo pode ocorrer nas seguintes circunstâncias:
- O gráfico contém um ciclo negativo.
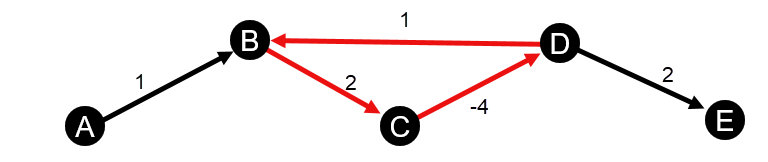
- O gráfico contém um auto-loop negativo.
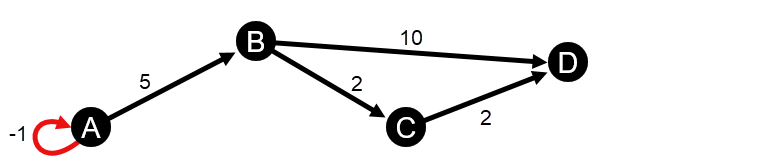
- O gráfico não é direcionado e contém uma extremidade negativa.
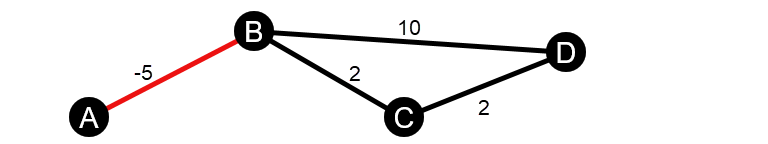
Próximas etapas
Teste estes exercícios baseados em cenários do Learn ArcGIS para fluxos de trabalho guiados com análise de links: