Análise de regressão—ArcGIS Insights

A análise de regressão é uma técnica de análise que calcula o relacionamento estimado entre uma variável dependente e uma ou mais variáveis explanatórias. Com a análise de regressão, você pode modelar o relacionamento entre as variáveis escolhidas, como também, prever valores com base no modelo.

Visão geral da análise de regressão

A análise de regressão utiliza um método de avaliação escolhido, uma variável dependente e uma ou mais variáveis explanatórias para criar uma equação que estima os valores para a variável dependente.

O modelo de regressão inclui saídas, como ^R2 e valores-p, para fornecer informações sobre como o modelo avalia a variável dependente.

Gráficos, como matrizes do gráfico de dispersão, histogramas, e gráficos de pontos, também podem ser utilizados na análise de regressão para analisar relacionamentos e suposições de teste.

A análise de regressão pode ser utilizada para resolver os seguintes tipos de problemas:

Determinar quais variáveis explanatórias estão relacionadas à variável dependente.
Entender o relacionamento entre as variáveis dependentes e explanatórias.
Prever valores desconhecidos da variável dependente.

Exemplos

Um analista de uma pequena cadeia de varejo está estudando o desempenho de diferentes lojas. O analista deseja saber o motivo de algumas lojas estarem tendo um volume de vendas inesperadamente baixo. O analista cria um modelo de regressão com variáveis explanatórias como idade mediana e renda na vizinhança, como também, a distância até centros de varejo e o transporte público, para determinar quais variáveis estão influenciando as vendas.

Um analista de um departamento de educação está estudando os efeitos dos programas de café da manhã na escola. O analista cria um modelo de regressão dos resultados de escolaridade, como a taxa de graduação, utilizando variáveis explanatórias como tamanho da turma, renda familiar, orçamento escolar per capita e proporção de alunos tomando café da manhã diariamente. A equação do modelo pode ser utilizada para determinar o efeito relativo de cada variável nos resultados de escolaridade.

O analista de uma organização não governamental está estudando as emissões globais de gases de efeito estufa. O analista cria um modelo de regressão para as emissões mais recentes para cada país utilizando variáveis explanatórias como produto interno bruto (PIB), população, produção de eletricidade utilizando combustíveis fósseis e uso de veículos. O modelo pode então ser utilizado para prever futuras emissões de gases de efeito estufa utilizando o PIB previsto e os valores da população.

Mínimos Quadrados Ordinários

A análise de regressão no ArcGIS Insights é modelada utilizando o método Mínimos Quadrados Ordinários (OLS).

O método OLS é uma forma de multiplicar a regressão linear, ou seja, o relacionamento entre as variáveis dependentes e as variáveis independentes deve ser modelado ao ajustar uma equação linear aos dados observados.

Um modelo OLS utiliza a seguinte equação:

y_i=β₀+β₁x₁+β₂x₂+...+β_nx_n+ε

Onde:

y_i=o valor observado da variável dependente no ponto i
β₀=o intercepto y (valor constante)
β_n=o coeficiente de regressão ou declividade para a variável explanatória N no ponto i
x_n=o valor da variável N no ponto i
ε=o erro da equação de regressão

Suposições

Cada método de regressão tem várias suposições que devem ser atendidas para que a equação seja considerada confiável. As suposições do OLS devem ser validadas ao criar um modelo de regressão.

As seguintes suposições devem ser testadas e atendidas ao utilizar o método OLS:

O modelo deve ser linear

A regressão OLS pode ser utilizada somente para criar um modelo linear. A linearidade pode ser testada entre a variável dependente e as variáveis explanatórias utilizando um gráfico de dispersão. Uma matriz do gráfico de dispersão pode testar todas as variáveis, desde que não haja mais do que cinco variáveis no total.

Os dados devem ser amostrados aleatoriamente

Os dados utilizados na análise de regressão devem ser amostrados de tal forma que as amostras em si não dependam de nenhum fator externo. A amostragem aleatória pode ser testada utilizando os residuais do modelo de regressão. Os residuais, que são uma saída do modelo de regressão, não devem ter correlação quando confrontados com as variáveis explanatórias em um gráfico de dispersão ou matriz do gráfico de dispersão.

As variáveis explanatórias não devem ser colineares

A colinearidade refere-se a um relacionamento linear entre variáveis explanatórias, o que cria redundância no modelo. Em alguns casos, o modelo pode ser criado com colinearidade. No entanto, se uma das variáveis colineares parecer dependente da outra, convém considerar a eliminação desta variável do modelo. A colinearidade pode ser testada utilizando um gráfico de dispersão ou matriz do gráfio de dispersão das variáveis explanatórias.

As variáveis explanatórias devem ter erro insignificante na medição

Um modelo de regressão é tão preciso quanto seus dados de entrada. Se as variáveis explanatórias tiverem grandes margens de erro, o modelo não poderá ser aceito como exato. Ao executar a análise de regressão, é importante utilizar somente conjuntos de dados de fontes conhecidas e confiáveis para garantir que o erro seja insignificante.

Os residuais têm uma soma esperada de zero

Residuais são a diferença entre os valores observados e estimados em uma análise de regressão. Valores observados que caem acima da curva de regressão terão um valor residual positivo e os valores observados que caírem abaixo da curva de regressão terão um valor residual negativo. A curva de regressão deve estar ao longo do centro dos pontos de dados; portanto, a soma dos residuais deve ser zero. A soma de um campo pode ser calculada em uma tabela de resumo.

Os residuais têm discrepância homogênea

A variação deve ser a mesma para todos os residuais. Esta suposição pode ser testada utilizando um gráfico de dispersão de residuais (eixo y) e valores estimados (eixo x). O gráfico de dispersão resultante deve aparecer como uma faixa horizontal de pontos plotados aleatoriamente no gráfico.

Os residuais são normalmente distribuídos

Uma distribuição normal, também denominada curva de sino, é uma distribuição que ocorre naturalmente, onde a frequência de um fenômeno é alta perto da média e diminui à medida que a distância da média aumenta. Uma distribuição normal é frequentemente utilizada como hipótese nula em uma análise de estatística. Os residuais devem ser normalmente distribuídos para mostrar que a linha de melhor ajuste é otimizada centralmente dentro dos pontos de dados observados, não inclinada em direção a alguns e longe de outros. Esta suposição pode ser testada criando um histograma com os residuais. A curva de distribuição normal pode ser sobreposta e medidas de assimetria e curtose são relatadas na parte de trás do cartão de histograma.

Residuais adjacentes não devem mostrar autocorrelação

Esta suposição é baseada em dados ordenados por tempo. Se os dados estiverem ordenados por tempo, cada ponto de dados deverá ser independente do ponto de dados anterior ou posterior. Portanto, é importante certificar-se que seus dados ordenados pelo tempo estejam organizados na ordem correta ao executar uma análise de regressão. Esta suposição pode ser calculada utilizando um teste de Durbin-Watson.

O teste Durbin-Watson é uma medida de autocorrelação em residuais de um modelo de regressão. O teste Durbin-Watson utiliza uma escala de 0 a 4, com valores de 0 a 2 indicando autocorrelação positiva, 2 indicando ausência de autocorrelação e 2 a 4 indicando autocorrelação negativa. Portanto, valores próximos a 2 são necessários para atender à hipótese de não haver autocorrelação nos residuais. Em geral, valores entre 1.5 e 2.5 são considerados aceitáveis, enquanto valores menores que 1.5 ou maiores que 2.5 indicam que o modelo não se encaixa na suposição de nenhuma autocorrelação.

Validade do modelo

A precisão de uma equação de regressão é uma parte importante da análise de regressão. Todos os modelos incluirão uma quantidade de erro, mas a compreensão das estatísticas ajudará você a determinar se o modelo poderá ser utilizado em sua análise ou se será necessário fazer ajustes.

Há duas técnicas para determinar a validade de um modelo de regressão: análise exploratória e análise confirmatória.

Análise explanatória

A análise exploratória é um método de entender seus dados utilizando uma variedade de técnicas visuais e de estatísticas. Ao longo de sua análise exploratória, você testará as suposições da regressão OLS e comparará a eficácia de diferentes variáveis explanatórias. A análise exploratória permitirá comparar a eficácia e a precisão de diferentes modelos, mas não determina se você deve utilizar ou rejeitar seu modelo. A análise exploratória deve ser realizada antes da análise confirmatória para cada modelo de regressão e reiterada para fazer comparações entre os modelos.

Os seguintes gráficos e estatísticas podem ser utilizados como parte da análise exploratória:

Gráfico de dispersão e matriz do gráfico de dispersão
Histograma e distribuição normal
Equação de regressão e previsão de novas observações
Coeficiente de determinação, ^R2 e ^R2 Ajustado
Erro padrão de residual
Gráfico de pontos

A análise exploratória deve começar enquanto você escolhe variáveis explanatórias e antes de criar um modelo de regressão. Como o OLS é um método de regressão linear, um das principais suposições é que o modelo deve ser linear. Um gráfico de dispersão ou matriz do gráfico de dispersão pode ser utilizado para avaliar a linearidade entre a variável dependente e as variáveis explanatórias. Uma matriz do gráfico de dispersão pode exibir até quatro variáveis explanatórias junto com a variável dependente, tornando-a uma ferramenta importante para comparações em larga escala entre todas as variáveis. Um único gráfico de dispersão exibe somente duas variáveis: uma dependente e uma independente ou explanatória. Visualizar um gráfico de dispersão da variável dependente e uma única variável explanatória permite a você fazer uma avaliação mais aguda da relação entre as variáveis. A linearidade pode ser testada antes de criar um modelo de regressão para ajudar a determinar quais variáveis explanatórias criarão um modelo aceitável.

Várias saídas de estatísticas estão disponíveis após a criação de um modelo de regressão, incluindo a equação de regressão, valor de ^R2 , e teste de Durbin-Watson. Após criar um modelo de regressão, você deverá utilizar os resultados e tabelas e gráficos necessários para testar o restante de suposições da regressão de OLS. Se o seu modelo atender as suposições, você poderá continuar com a análise exploratória restante.

A equação de regressão fornece informações valiosas sobre a influência de cada variável explanatória nos valores previstos, incluindo o coeficiente de regressão para cada variável explanatória. Os valores de declividade podem ser comparados para determinar a influência relativa de cada variável explanatória na variável dependente; quanto mais longe o valor de declividade estiver de zero (positivo ou negativo), maior a influência. A equação de regressão também pode ser utilizada para prever valores para a variável dependente, inserindo valores para cada variável explanatória.

O coeficiente de determinação, simbolizado como ^R2, mede quão bem a equação de regressão modela os pontos de dados reais. O valor ^R2 é um número entre 0 e 1, com valores mais próximos de 1, indicando modelos mais precisos. Um valor ^R2 de 1 indica um modelo perfeito, o que é altamente improvável em situações do mundo real, dada a complexidade das interações entre diferentes fatores e variáveis desconhecidas. Portanto, você deve se esforçar para criar um modelo de regressão com o valor ^R2 o mais alto possível, ao reconhecer que o valor poderá não estar próximo de 1.

Ao executar a análise de regressão, há o risco de criar um modelo de regressão que tenha um valor de ^R2 aceitável, adicionando variáveis explanatórias que causam um melhor ajuste baseado somente no acaso. O valor ^R2 ajustado, que também é um valor entre 0 e 1, representa variáveis explanatórias adicionais, reduzindo o papel que o acaso desempenha no cálculo. O ^R2 ajustado deve ser utilizado para modelos com muitas variáveis explanatórias, ou ao comparar modelos com diferentes números de variáveis explanatórias.

O erro padrão residual mede a precisão com a qual o modelo de regressão pode prever valores com novos dados. Valores menores indicam um modelo mais preciso; portanto, quando vários modelos são comparados, o modelo com o menor valor será o modelo que minimizará o erro padrão residual.

Gráficos de pontos podem ser utilizados para analisar suas variáveis explanatórias em busca de padrões como agrupamentos e valores atípicos, que podem afetar a precisão do modelo.

Análise confirmatória

A análise confirmatória é o processo de testar seu modelo contra uma hipótese nula. Na análise de regressão, a hipótese nula é que não há relação entre a variável dependente e as variáveis explanatórias. Um modelo sem relacionamento teria valores de declividade 0. Se os elementos de sua análise confirmatória forem estatisticamente significativos, você poderá rejeitar a hipótese nula (em outras palavras, a significância estatística indica que existe um relacionamento entre as variáveis dependentes e explanatórias).

Os seguintes resultados de estatística são utilizados para determinar a significância como parte da análise confirmatória:

Estatística F e seu valor p associado
Estatística t e seus valores p associados
Intervalos de confiança

A estatística F é uma estatística global retornada de um teste F, que indica a capacidade preditiva do modelo de regressão, determinando se todos os coeficientes de regressão no modelo são significativamente diferentes de 0. O teste F analisa a influência combinada das variáveis explanatórias, em vez de testar as variáveis explanatórias individualmente. A estatística F tem um valor p associado, o que indica a probabilidade de que os relacionamentos nos seus dados estejam acontecendo por acaso. Já que os valores p são baseados em probabilidades, os valores são fornecidos em uma escala de 0.0 a 1.0. Um valor p pequeno, geralmente 0.05 ou menor, é necessário para determinar que os relacionamentos no modelo são reais (em outras palavras, não acontecendo por acaso) e para rejeitar a hipótese nula. Neste caso, a probabilidade dos relacionamentos no modelo estarem acontecendo por acaso é de 0.05, ou 1 em 20. Alternativamente, a probabilidade de que os relacionamentos sejam reais é de 0.95, ou 19 em 20.

A estatística t é uma estatística local retornada de um teste t, que indica a capacidade preditiva de cada variável explanatória individualmente. Como o teste F, o teste t analisa se os coeficientes de regressão no modelo são significativamente diferentes de zero. No entanto, como é realizado um teste t em cada variável explanatória, o modelo retornará um valor de estatística t para cada variável explanatória, em vez de um por modelo. Cada estatística t tem um valor p associado, o que indica a significância da variável explanatória. Como os valores p para o teste F, o valor p para cada teste t deve ser 0.05 ou menor para rejeitar a hipótese nula. Se uma variável explanatória tiver um valor p maior que 0.05, a variável deverá ser descartada e um novo modelo deverá ser criado, mesmo que o valor p global seja significativo.

Intervalos de confiança mostram o coeficiente de regressão para cada variável explanatória e os intervalos de confiança de 90, 95 e 99 por cento associados. Portanto, os intervalos de confiança podem ser utilizados juntamente com os valores-p dos testes t para avaliar a hipótese nula para variáveis explanatórias individuais. Os coeficientes de regressão não devem ser iguais a 0 para rejeitar a hipótese nula e continuar utilizando o modelo. Portanto, para cada variável explicativa, o coeficiente de regressão e os intervalos de confiança associados não devem se sobrepor a 0. Se um intervalo de confiança de 99 ou 95 por cento para uma determinada variável explicativa se sobrepõe a 0, a variável explicativa falhou em rejeitar a hipótese nula. A inclusão desta variável em seu modelo pode afetar a importância geral do seu modelo. Se somente o intervalo de confiança de 90 por cento se sobrepuser a 0, a variável explanatória poderá ser incluída no modelo, desde que as outras estatísticas globais sejam significativas. Idealmente, os intervalos de confiança para todas as variáveis explanatórias devem estar longe de 0.

Outras saídas

Outras saídas, como valores estimados e residuais, são importantes para testar as suposições da regressão de OLS. Nesta seção, você aprenderá mais sobre como estes valores são calculados.

Valores estimados

Os valores estimados são calculados utilizando a equação de regressão e os valores para cada variável explanatória. Idealmente, os valores estimados seriam iguais aos valores observados (em outras palavras, os valores reais da variável dependente).

Os valores estimados são utilizados com os valores observados para calcular residuais.

Residuais

Os valores residuais em uma análise de regressão são as diferenças entre os valores observados no conjunto de dados e os valores estimados, calculados com a equação de regressão.

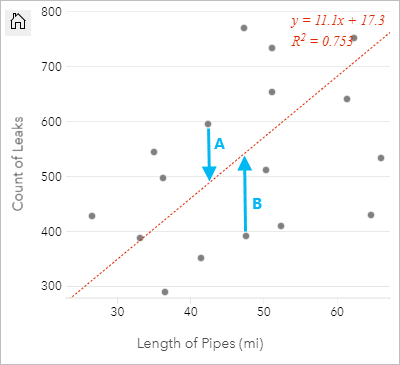
Os residuais A e B para o relacionamento acima seriam calculados da seguinte maneira:

residuals_A = observed_A - estimated_A residuals_A = 595 - 487.62 residuals_A = 107.38

residuals_B = observed_B - estimated_B residuals_B = 392 - 527.27 residuals_B = -135.27

Residuais podem ser utilizados para calcular erros em uma equação de regressão, como também, para testar várias suposições.

Comentário neste tópico?