Гистограммы агрегируют числовые данные по группам с равными интервалами, которые называют бинами, и отображают частоту встречаемости значений в каждом из бинов. Гистограмма создается с помощью числового поля или поля доля/отношение.
Гистограммы помогают получить ответ на такой вопрос: каково распределение числовых значений и частота их появлений в наборе данных? Есть ли выбросы?
Пример
Негосударственная организация в области здравоохранения изучает показатели подросткового ожирения в США. Гистограмма частоты случаев ожирения у подростков может использоваться для того, чтобы определить, как распределены показатели ожирения по штатам, в том числе наиболее высокие и низкие показатели частоты ожирения и их общий уровень.
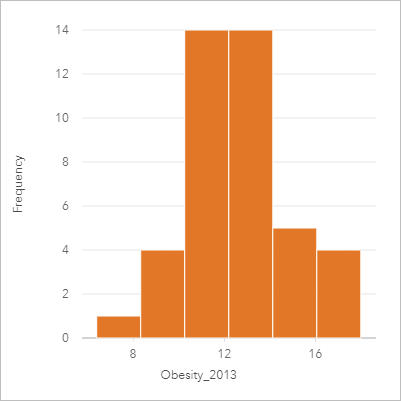
На приведенной выше гистограмме показано нормальное распределение, при котором наиболее часто встречающиеся показатели находятся в диапазоне 10-14 процентов.
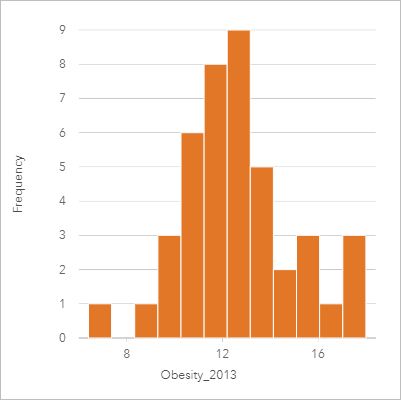
Увеличивая и уменьшая число бинов, вы можете повлиять на характер анализа своих данных. Хотя сами данные и не изменяются, может измениться их вид. Чтобы правильно истолковать закономерности в данных, важно выбрать подходящее число бинов. Слишком маленькое число бинов может скрыть какие-то закономерности, а слишком большое – преувеличить значение небольших, допустимых изменений данных. Ниже представлен пример подходящего числа бинов данных. Каждый бин содержит примерно один процент данных, и данные можно рассмотреть в более крупном масштабе, что позволит выявить закономерности, невидимые при использовании шести бинов. В данном случае налицо нормальное распределение значений с незначительным сдвигом влево.
Создать гистограмму
Для создания гистограммы выполните следующие шаги:
- Выберите числовое поле
или поле доли/отношения 
.Подсказка:
Вы можете выполнять поиск по полям с помощью строки поиска в панели данных.
- Для создания гистограммы выполните следующие шаги:
- Перетащите выбранные поля в новую карточку.
- Наведите курсор над областью размещения Диаграмма.
- Поместите выбранные поля на Гистограмму.
Подсказка:
Также можно построить диаграммы с помощью меню Диаграмма над панелью данных или кнопки Тип визуализации 
на существующей карточке. В меню Диаграммы будут доступны только диаграммы, которые применимы к имеющейся выборке данных. В меню Тип визуализации будут только подходящие варианты визуализаций (карты, диаграммы или таблицы).
Гистограмму также можно создать с помощью Просмотр гистограммы; для этого используйте кнопку Действие 
на вкладке Найти ответы > Распределение
Примечания по использованию
Гистограммы обозначаются отдельными символами. Вы можете использовать кнопку Опции слоя 
, чтобы изменить цвет символа и цвет контура, который будет применен ко всем бинам.
Когда гистограмма будет создана, Insights автоматически вычисляет приблизительное количество бинов для отображения ваших данных. Вы можете изменить количество бинов при помощи бегунка вдоль оси Х или щёлкнув на числе бинов и введя новое значение.
Примечание:
Если выбранное количество бинов не делится точно на диапазон данных, то бины будут вычислены как десятичные значения. Гистограммы показывают в качестве надписей бинов округленные целые, а не десятичные. Округленные целые числа нужны только для отображения, для всех вычислений используются десятичные значения. В случае, если бин включает значения данных, близкие к верхнему или нижнему пределу, а надпись округлена, начальное и конечное значения ячейки могут отображаться некорректно, поскольку надписи отображают округленные значения, а не десятичные дроби.
Для отображения среднего, медианного и нормального распределения данных используйте кнопку Статистика диаграммы 
. Кривая нормального распределения представляет ожидаемое распределение случайного поднабора непрерывных данных, где самая высокая частота значений центрируется вокруг среднего и частота значений уменьшается по мере увеличения или уменьшения значений по мере удаления от среднего. Кривая нормального распределения полезна при выявлении наличия провалов и выбросов в данных.
Используйте кнопку Тип визуализации для прямого переключения между гистограммой и градуированными символами на карте или суммарной таблицей.
Используйте кнопку Перевернуть карточку 
, чтобы посмотреть обратную сторону карточки. Вкладка Информация о карточке 
предоставляет информацию о данных на карточке, а вкладка Экспорт данных 
позволяет пользователям экспортировать данные с карточки.
Эти статистики на обороте карточек включают среднее, медиану, дисперсию, стандартное квадратичное отклонение, эксцесс и сдвиг (упрощенный). Следующая таблица содержит описание асимметрии и эксцесса:
| Статистика | Описание |
|---|---|
Скошенность | Скошенность определяет симметрично ли распределение данных. Мера скошенности определяет где лежит большинство значений в распределении – левее или правее среднего. Асимметрия нормального распределения равна нулю и показывает одинаковый объем данных по обе стороны от среднего. Значения асимметрии могут быть нулевыми, отрицательными или положительными:
|
Эксцесс | Эксцесс описывает форму плотности распределения и определяет вероятность выбросов при данном распределении. Распределения с относительно тяжёлыми хвостами называются островершинными (лептокуртическими), и у них эксцесс больше нуля. Распределения с относительно тонкими хвостами называются плосковершинными (платикуртическими), и у них эксцесс меньше нуля. Эксцесс нормального распределения равен трём, а в случае использования упрощённого эксцесса – нулю (это вычисляется по той же формуле, что и эксцесс, минус три). Значения упрощённого эксцесса могут быть нулевыми, отрицательными или положительными:
|