Analisi di regressione—ArcGIS Insights

L'analisi di regressione è una tecnica che calcola la relazione stimata tra una variabile dipendente e una o più variabili esplicative. Con l'analisi di regressione, è possibile definire la relazione tra le variabili scelte e prevedere i valori in base al modello.

L'analisi di regressione utilizza un metodo di stima specificato, una variabile dipendente e una o più variabili esplicative per creare un'equazione che stima i valori per la variabile dipendente.

Il modello di regressione include output, come R² e valori P, per fornire informazioni sulla precisione della stima della variabile dipendente da parte del modello.

I grafici, come le matrici di grafici a dispersione, gli istogrammi e i grafici di punti, possono anche essere utilizzati nell'analisi di regressione per analizzare le relazioni e testare i presupposti.

L'analisi di regressione può essere utilizzata per risolvere i seguenti tipi di problemi:

Determinare le variabili esplicative sono correlate alla variabile dipendente.
Comprendere la relazione tra le variabili dipendenti ed esplicative.
Prevedere i valori sconosciuti della variabile dipendente.

Esempi

Di seguito sono riportati scenari di esempio per l'uso dll'analisi di regressione:

Un analista di una piccola catena di negozi studia le prestazioni di diversi negozi. L'analista vuole sapere perché alcuni negozi hanno un volume di vendite inaspettatamente basso. L'analista crea un modello di regressione con variabili esplicative come l'età media e il reddito nei quartieri nelle vicinanze, nonché la distanza dai centri commerciali e il trasporto pubblico, per stabilire quali variabili influenzano le vendite.
Un analista per un dipartimento di istruzione studia gli effetti dei programmi di colazione scolastica. L'analista crea un modello di regressione dei risultati del rendimento scolastico, come il tasso di diplomati, utilizzando variabili esplicative come la dimensione della classe, il reddito familiare, il budget scolastico pro capite e la proporzione di studenti che fanno colazione ogni giorno. L'equazione del modello può essere utilizzata per determinare l'effetto relativo di ogni variabile sui risultati del rendimento scolastico.
Un analista di un'organizzazione non governativa studia le emissioni globali di gas serra. L'analista crea un modello di regressione per le ultime emissioni per ciascun paese utilizzando variabili esplicative quali il prodotto interno lordo (PIL), la popolazione, la produzione di elettricità mediante combustibili fossili e l'utilizzo dei veicoli. Il modello può quindi essere utilizzato per prevedere le future emissioni di gas serra utilizzando il PIL previsto e i valori della popolazione.

Quadrati Meno Ordinari

L'analisi di regressione in ArcGIS Insights viene definita utilizzando il metodo OLS (minimi quadrati).

Il metodo OLS (minimi quadrati) è una forma di regressione lineare multipla, il che significa che la relazione tra le variabili dipendenti e le variabili indipendenti deve essere definita adattando un'equazione lineare ai dati osservati.

Un modello OLS utilizza la seguente equazione:

y_i=β₀+β₁x₁+β₂x₂+...+β_nx_n+ε

dove:

y_i=il valore osservato della variabile dipendente sul punto i
β₀=l’intercettazione y (valore costante)
β_n=il coefficiente di regressione o la pendenza per la variabile esplicativa N sul punto i
x_n=il valore della variabile N sul punto i
ε=l’errore dell’equazione di regressione

Presupposti

Ogni metodo di regressione ha diverse ipotesi che devono essere soddisfatte affinché l'equazione sia considerata affidabile. Le ipotesi OLS devono essere convalidate quando si crea un modello di regressione.

Le ipotesi descritte nelle sezioni che seguono dovrebbero essere testate e soddisfatte quando si utilizza il metodo OLS.

Il modello deve essere lineare

La regressione OLS può essere utilizzata solo per creare un modello lineare. La linearità può essere verificata tra la variabile dipendente e le variabili esplicative utilizzando un grafico a dispersione. Una matrice di grafico a dispersione può testare tutte le variabili, purché non vi siano più di cinque variabili in totale.

I dati devono essere campionati casualmente

I dati utilizzati nell'analisi di regressione devono essere campionati in modo tale che i campioni non dipendano da alcun fattore esterno. Il campionamento casuale può essere testato usando i residui del modello di regressione. I residui, che sono un output del modello di regressione, non devono avere alcuna correlazione quando sono tracciati rispetto alle variabili esplicative su un grafico a dispersione o una matrice di grafico a dispersione.

Le variabili esplicative non devono essere collineari

Per collinearità si intende una relazione lineare tra variabili esplicative, che crea ridondanza nel modello. In alcuni casi, il modello può essere creato con collinearità. Tuttavia, se una delle variabili collineari sembra dipendere dall'altra, si consiglia di eliminare tale variabile dal modello. La collinearità può essere testata utilizzando un grafico a dispersione o una matrice di grafico a dispersione delle variabili esplicative.

Le variabili esplicative devono avere un errore di misurazione trascurabile.

Un modello di regressione è preciso solo come i suoi dati di input. Se le variabili esplicative presentano ampi margini di errore, il modello non può essere accettato come preciso. Quando si esegue l'analisi di regressione, è importante utilizzare solo dataset provenienti da fonti note e attendibili per garantire che l'errore sia trascurabile.

I residui hanno una somma prevista pari a zero.

I residui sono la differenza tra i valori osservati e stimati in un'analisi di regressione. I valori osservati che si trovano al di sopra della curva di regressione hanno un valore residuo positivo e i valori osservati che scendono al di sotto della curva di regressione hanno un valore residuo negativo. La curva di regressione deve trovarsi lungo il centro dei punti dati e, la somma dei residui deve essere zero. La somma di un campo può essere calcolata in una tabella di riepilogo.

I residui hanno una varianza omogenea

La varianza deve essere la stessa per tutti i residui. Questa ipotesi può essere testata utilizzando un grafico a dispersione dei valori residui (asse y) e dei valori stimati (asse x). Il grafico a dispersione risultante dovrebbe apparire come una banda orizzontale di punti tracciati casualmente attraverso il grafico.

I residui sono distribuiti normalmente

Una distribuzione normale, detta anche curva a campana, è una distribuzione che si verifica normalmente, in cui la frequenza di un fenomeno è elevata vicino alla media e si riduce quando la distanza dalla media aumenta. Una distribuzione normale viene spesso utilizzata come ipotesi nulla in un'analisi statistica. I residui devono essere distribuiti normalmente per mostrare che la linea di miglior adattamento è ottimizzata centralmente all'interno dei punti dati osservati, non con una distorsione verso alcuni e lontana dagli altri. Questa ipotesi può essere testata creando un istogramma con i residui. La curva di distribuzione normale può essere sovrapposta e le misure di asimmetria e sono riportate sul retro della scheda di istogramma.

I residui adiacenti non devono mostrare autocorrelazione.

Questa ipotesi è basata su dati ordinati nel tempo. Se i dati sono ordinati nel tempo, ogni punto dati deve essere indipendente dal punto dati precedente o successivo. È importante assicurarsi che i dati ordinati nel tempo siano organizzati nell'ordine corretto quando si esegue un'analisi di regressione. Questa ipotesi può essere calcolata utilizzando il test di Durbin-Watson.

Il test di Durbin-Watson è una misura di autocorrelazione nei residui in un modello di regressione. Il test di Durbin-Watson utilizza una scala da 0 a 4, con valori da 0 a 2 che indicano l'autocorrelazione positiva, 2 che indica l'assenza di autocorrelazione e da 2 a 4 che indicano l'autocorrelazione negativa. I valori vicini a 2 sono necessari per soddisfare l'ipotesi di non autocorrelazione nei residui. In generale, valori compresi tra 1,5 e 2,5 sono considerati accettabili, mentre valori inferiori a 1,5 o superiori a 2,5 indicano che il modello non rientra nell'ipotesi di nessuna autocorrelazione.

Validità del modello

L'accuratezza di un'equazione di regressione è una parte importante dell'analisi di regressione. Tutti i modelli includono una quantità di errori ma la comprensione delle statistiche consente di determinare se il modello può essere utilizzato nell'analisi o se è necessario apportare modifiche.

Esistono due tecniche per determinare la validità di un modello di regressione: l'analisi esplorativa e l'analisi di conferma, descritte nelle sezioni che seguono.

Analisi esplorativa

L'analisi esplorativa è un metodo per comprendere i dati utilizzando una varietà di tecniche visive e statistiche. Nel corso di un'analisi esplorativa, sarà possibile testare le ipotesi di regressione OLS (minimi quadrati) e confrontare l'efficacia delle diverse variabili esplicative. L'analisi esplorativa consente di confrontare l'efficacia e l'accuratezza dei diversi modelli ma non determina se si deve usare o rifiutare un modello. L'analisi esplorativa deve essere eseguita prima dell'analisi di conferma per ogni modello di regressione e ripetuta per effettuare confronti tra i modelli.

I grafici e le statistiche che seguono possono essere utilizzati come parte dell'analisi esplorativa:

Grafico a dispersione e matrice di grafico a dispersione
Istogramma e distribuzione normale
Equazione di regressione e previsione di nuove osservazioni
Coefficiente di determinazione, R² e valore R² aggiustato
Errore standard residuo
Grafico di punti

L'analisi esplorativa deve iniziare mentre si scelgono le variabili esplicative e prima di creare un modello di regressione. Poiché OLS è un metodo di regressione lineare, una delle ipotesi principali è che il modello deve essere lineare. Un grafico a dispersione o una matrice di grafici a dispersione possono essere utilizzati per valutare la linearità tra la variabile dipendente e le variabili esplicative. Una matrice di grafici a dispersione può visualizzare fino a quattro variabili esplicative insieme alla variabile dipendente, rendendola un importante strumento per confronti su larga scala tra tutte le variabili. Un solo grafico a dispersione visualizza solo due variabili: una dipendente e una indipendente o esplicativa. La visualizzazione di un grafico a dispersione della variabile dipendente e di un'unica variabile esplicativa consente di effettuare una valutazione più precisa della relazione tra le variabili. La linearità può essere testata prima di creare un modello di regressione per aiutare a determinare quali variabili esplicative creeranno un modello accettabile.

Sono disponibili diversi output statistici dopo aver creato un modello di regressione, tra cui l'equazione di regressione, il valore R² e il test di Durbin-Watson. Una volta creato un modello di regressione, è necessario utilizzare gli output, i grafici e le tabelle necessarie per testare le ipotesi rimanenti di regressione OLS. Se il modello soddisfa le ipotesi, è possibile continuare con le restanti analisi esplorative.

L'equazione di regressione fornisce informazioni preziose sull'influenza di ogni variabile esplicativa sui valori previsti, compreso il coefficiente di regressione per ogni variabile esplicativa. I valori di pendenza possono essere confrontati per determinare l'influenza relativa di ogni variabile esplicativa sulla variabile dipendente; più il valore di pendenza è da zero (positivo o negativo), maggiore è l'influenza. L'equazione di regressione può anche essere utilizzata per prevedere i valori della variabile dipendente inserendo i valori per ogni variabile esplicativa.

Il coefficiente di determinazione, rappresentato con R², misura la precisione con cui l'equazione di regressione definisce i punti dati effettivi. Il valore R² è un numero compreso tra 0 e 1, con i valori più vicini a 1 che indicano modelli più accurati. Un valore R² pari a 1 indica un modello perfetto, che è altamente improbabile nelle situazioni reali, data la complessità delle interazioni tra diversi fattori e variabili sconosciute. Si deve cercare di creare un modello di regressione con il valore R² più alto possibile, pur riconoscendo che il valore potrebbe non essere vicino a 1.

Quando si esegue un'analisi di regressione, esiste il rischio di creare un modello di regressione che abbia un valore R² accettabile aggiungendo variabili esplicative che causano un adattamento migliore basato sulla sola probabilità. Il valore R² aggiustato, che è anche un valore compreso tra 0 e 1, tiene conto di ulteriori variabili esplicative, riducendo il ruolo che la probabilità svolge nel calcolo. Il valore R² aggiustato deve essere usato per i modelli che utilizzano molte variabili esplicative, o quando si confrontano modelli con diversi numeri di variabili esplicative.

L'errore standard residuo misura l'accuratezza con cui il modello di regressione può prevedere i valori con nuovi dati. Valori più piccoli indicano un modello più accurato; quando si confrontano più modelli, il modello con il valore più piccolo sarà il modello che riduce al minimo l'errore standard residuo.

I grafici di punti possono essere utilizzati per analizzare le variabili esplicative per modelli come clustering e outlier, che possono influenzare l'accuratezza del modello.

Analisi di conferma

L'analisi di conferma è il processo di verifica di un modello rispetto a un'ipotesi nulla. Nell'analisi di regressione, l'ipotesi nulla consiste nell'assenza di una qualsiasi relazione tra la variabile dipendente e le variabili esplicative. Un modello senza relazione avrebbe valori di pendenza pari a 0. Se gli elementi dell'analisi di conferma sono statisticamente significativi, è possibile scartare l'ipotesi nulla (in altre parole, la rilevanza statistica indica che esiste una relazione tra le variabili dipendenti e le variabili esplicative).

I seguenti output statistici vengono utilizzati per determinare la rilevanza nell'ambito dell'analisi di conferma:

Statistica F e relativo valore p associato
Statistica t e relativi valori p associati
Intervalli di affidabilità

La statistica F è una statistica globale restituita da un test F, che indica la capacità predittiva del modello di regressione determinando se tutti i coefficienti di regressione del modello sono significativamente diversi da 0. Il test F analizza l'influenza combinata delle variabili esplicative, piuttosto che testare individualmente le variabili esplicative. La statistica F ha un valore p associato, che indica la probabilità che le relazioni nei dati si verifichino per caso. Poiché i valori di p sono basati sulle probabilità, i valori sono indicati su una scala da 0,0 a 1,0. Un piccolo valore p, solitamente 0,05 o meno, è necessario per determinare che le relazioni nel modello sono reali (in altre parole, non si verificano per caso) e per rifiutare l'ipotesi nulla. In tal caso, la probabilità che le relazioni nel modello si verifichino per caso è di 0,05, ovvero 1 su 20. In alternativa, la probabilità che le relazioni siano reali è di 0,95, o 19 su 20.

La statistica t è una statistica locale restituita da un test t, che indica la capacità predittiva di ogni variabile esplicativa singolarmente. Come il test F, il test t analizza se i coefficienti di regressione nel modello sono significativamente diversi da zero. Tuttavia, poiché viene eseguito un test t su ogni variabile esplicativa, il modello restituirà un valore statistico t per ogni variabile esplicativa, piuttosto che uno per modello. A ogni statistica t è associato un valore p, che indica la rilevanza della variabile esplicativa. Come i valori p per il test F, il valore p per ogni test t dovrebbe essere pari o inferiore a 0,05 per rifiutare l'ipotesi nulla. Se una variabile esplicativa ha un valore p superiore a 0,05, la variabile dovrebbe essere scartata e dovrebbe essere creato un nuovo modello, anche se il valore globale p era significativo.

Gli intervalli di affidabilità mostrano il coefficiente di regressione per ogni variabile esplicativa e gli intervalli di affidabilità associati del 90%, 95% e 99%. Gli intervalli di affidabilità possono essere utilizzati insieme ai valori p dei test t per valutare l'ipotesi nulla delle singole variabili esplicative. I coefficienti di regressione non devono essere uguali a 0 se si vuole rifiutare l'ipotesi nulla e continuare a utilizzare il modello. Per ogni variabile esplicativa, il coefficiente di regressione e gli intervalli di affidabilità associati non dovrebbero sovrapporsi a 0. Se un intervallo di affidabilità del 99 o 95 percento si sovrappone a 0, la variabile esplicativa non è riuscita a rifiutare l'ipotesi nulla. Includere una tale variabile nel modello può avere un effetto sulla rilevanza complessiva dello stesso. Se solo l'intervallo di affidabilità del 90% si sovrappone a 0, la variabile esplicativa può essere inclusa nel modello purché le altre statistiche globali siano rilevanti. Idealmente, gli intervalli di affidabilità per tutte le variabili esplicative dovrebbero essere lontani da 0.

Altri output

Altri output, come valori stimati e residui, sono importanti per testare le ipotesi di regressione OLS. Nelle sezioni che seguono è descritta la modalità di calcolo di tali valori.

Valori stimati

I valori stimati sono calcolati utilizzando l'equazione di regressione e i valori per ogni variabile esplicativa. Idealmente, i valori stimati sarebbero uguali ai valori osservati (in altre parole, i valori effettivi della variabile dipendente).

I valori stimati sono utilizzati con i valori osservati per calcolare i residui.

Residui

I valori residui in un'analisi di regressione sono le differenze tra i valori osservati nel dataset e i valori stimati calcolati con l'equazione di regressione.

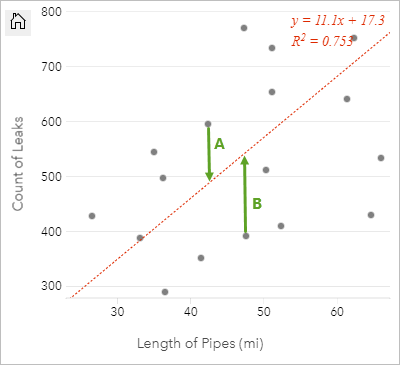
I residui A e B per le relazioni precedenti vengono calcolati come segue:

residui_A = osservati_A - stimati_A residui_A = 595 - 487.62 residui_A = 107.38

residui_B = osservati_B - stimati_B residui_B = 392 - 527.27 residui_B = -135.27

I residui possono essere utilizzati per calcolare l'errore in un'equazione di regressione e per testare diverse ipotesi.

Qualche feedback su questo argomento?