


L’analyse de liens est une technique centrée sur les relations et les connexions dans un jeu de données. Elle permet de calculer les mesures de centralité (c’est-à-dire le degré, l’intermédiarité, la proximité et le vecteur propre) et de visualiser les connections dans un diagramme de liens ou une carte de liens.
À propos de l’analyse de liens
L’analyse de liens utilise un réseau de liens et de nœuds interconnectés pour identifier et analyser les relations difficilement visibles dans les données brutes. Les types de réseaux courants sont notamment :
- Réseaux sociaux qui indiquent qui parle à qui.
- Réseaux sémantiques qui illustrent des thèmes associés les uns aux autres.
- Réseaux de conflits indiquant les alliances de connexions entre des joueurs.
- Réseaux aériens indiquant quels aéroports ont des vols en correspondance.
Exemples
Un analyste de la criminalité mène une enquête sur un réseau criminel. Les données extraites des enregistrements des téléphones portables peuvent servir à déterminer la relation et la hiérarchie entre les membres du réseau.
Une société de cartes de crédit met au point un nouveau système visant à détecter les vols de cartes de crédit. Le système utilise les modèles connus de transactions pour chaque client, tels que la ville, les points de vente et les types de transactions, pour identifier les anomalies et alerter le client de tout vol potentiel.
Un analyste de santé publique effectue des recherches sur la crise des opioïdes en Amérique du Nord. L’analyste utilise les données des prescriptions et démographiques pour identifier les nouveaux modèles qui émergent avec l’étendue de la crise.
Fonctionnement de l’outil Analyse de liens
Le tableau suivant présente une vue d’ensemble de la terminologie de l’analyse de liens :
| Période | Description | Exemples |
|---|---|---|
Réseau | Ensemble de nœuds et de liens interconnectés. | Réseau social en ligne qui utilise un réseau de profils et de relations pour connecter des utilisateurs. Réseaux aériens qui utilisent un réseau d’aéroports et de vols pour transporter des voyageurs de leur lieu d’origine vers leur destination. |
Nœud | Point ou sommet qui représente un objet, tel qu’une personne, un lieu, un type de délit ou un tweet. Des propriétés peuvent également être associées au nœud. | Profils dans un réseau social. Les propriétés associées sont notamment le nom de l’utilisateur, sa ville natale ou son employeur. Aéroports dans un réseau aérien. Les propriétés associées sont notamment le nom de l’aéroport. |
Lien | Relations ou connexions entre des nœuds. Des propriétés peuvent également être associées au lien. | Relation entre différents profils du réseau, telle qu’un ami, un suiveur ou une relation. Les propriétés associées sont notamment la durée de la relation. Vols entre différents aéroports dans un réseau aérien. Les propriétés associées sont notamment le nombre de vols entre différents aéroports. |
Centralité
La centralité mesure l’importance des nœuds dans un réseau.
La centralité est globalement utilisée aux fins suivantes :
- Pour évaluer l’influence d’un nœud sur les autres nœuds du réseau. Par exemple, quel utilisateur partagera une information ou une offre d’emploi avec le plus grand nombre d’utilisateurs ?
- Pour identifier les nœuds qui subissent le plus l’influence d’autres nœuds. Par exemple, quel aéroport va être le plus affecté par l’annulation des vols suite à une tempête qui a frappé une autre région ?
- Pour observer le flux ou la dispersion de quelque chose dans tout le réseau, notamment des informations, des objets ou des phénomènes. Par exemple, comment un colis est-il transporté du dépôt à l’adresse de livraison ?
- Pour comprendre quels nœuds dispersent les phénomènes à travers le réseau avec le plus d’efficacité. Par exemple, quel journal ou canal d’information doit être contacté afin que le plus de personnes possible soit au courant de l’histoire ?
- Pour localiser les nœuds susceptibles de bloquer ou d’empêcher la dispersion des phénomènes. Par exemple, où les centres de vaccination doivent-ils se situer pour enrayer la propagation d’un virus ?
Vous pouvez mesurer la centralité selon quatre modalités dans Insights : centralité de degré, centralité d’intermédiarité, centralité de proximité et centralité de vecteur propre.
Les calculs d’intermédiarité, de proximité et de centralité de vecteur propre peuvent être pondérés ou non pondérés.
Centralité de degré
La centralité de degré repose sur le nombre de connexions directes que possède un nœud. Vous devez l’utiliser pour déterminer quels nœuds ont le plus d’influence directe. Par exemple, dans un réseau social, les utilisateurs qui ont le plus grand nombre de connexions bénéficient d’une centralité de degré plus élevée.
La centralité de degré du nœud x est calculée à l’aide de l’équation suivante :
degCentrality(x)=deg(x)/(NodesTotal-1)où :
- NodesTotal = nombre de nœuds dans le réseau
- deg(x) = nombre de nœuds connectés au nœud x
Si les liens sont dirigés, c’est-à-dire que les informations transitent entre les nœuds dans une seule direction, alors la centralité de degré peut se mesurer en degré entrant ou en degré sortant. Dans le cas d’un réseau social, le degré entrant repose sur le nombre de profils que l’utilisateur suit, tandis que le degré sortant repose sur le nombre de personnes qui le suivent.
La centralité de degré entrant est calculée à l’aide de l’équation suivante :
indegCentrality(x)=indeg(x)/(NodesTotal-1)où :
- NodesTotal = nombre de nœuds dans le réseau
- indeg(x) = nombre de nœuds connectés au nœud x, le flux étant dirigé vers le nœud x
La centralité de degré sortant est calculée à l’aide de l’équation suivante :
outdegCentrality(x)=outdeg(x)/(NodesTotal-1)où :
- NodesTotal = nombre de nœuds dans le réseau
- outdeg(x) = nombre de nœuds connectés au nœud x, le flux s’éloignant du nœud x
Pour les diagrammes dirigés, Insights dimensionne par défaut les nœuds par centralité de degré sortant.
Centralité d’intermédiarité
La centralité d’intermédiarité repose sur la mesure dans laquelle un nœud fait partie du chemin le plus court entre d’autres nœuds. Vous devez l’utiliser pour déterminer quels nœuds sont utilisés pour connecter d’autres nœuds les uns aux autres. Par exemple, un utilisateur dans un réseau social qui a des connexions vers plusieurs groupes d’amis aura une centralité d’intermédiarité plus élevée que des utilisateurs dont les connexions se trouvent dans un groupe unique.
La centralité d’intermédiarité du nœud x est calculée à l’aide de l’équation suivante :
btwCentrality(x)=Σa,bϵNodes(pathsa,b(x)/pathsa,b)où :
- Nodes = tous les nœuds du réseau
- pathsa,b = nombre de chemins les plus courts entre tous les nœuds a et b
- pathsa,b(x) = nombre de chemins les plus courts entre tous les nœuds a et b qui se connectent via le nœud x
L’équation de centralité d’intermédiarité ci-dessus ne tient pas compte de la taille du réseau. Ainsi, les valeurs de centralité d’intermédiarité des réseaux de grande taille ont tendance à être supérieures à celles des réseaux de petite taille. Pour comparer des réseaux de différentes tailles, vous devez normaliser l’équation de centralité d’intermédiarité en divisant le nombre de paires de nœuds dans le diagramme.
L’équation suivante permet de normaliser un diagramme non dirigé :
1/2(NodesTotal-1)(NodesTotal-2)où :
- NodesTotal = nombre de nœuds dans le réseau
L’équation suivante permet de normaliser un diagramme dirigé :
(NodesTotal-1)(NodesTotal-2)où :
- NodesTotal = nombre de nœuds dans le réseau
Centralité de proximité
La centralité de proximité repose sur la moyenne de la distance du plus court chemin réseau entre les nœuds. Vous devez l’utiliser pour déterminer quels nœuds sont le plus étroitement associés aux autres nœuds du réseau. Par exemple, un utilisateur dont le nombre de connexions dans le réseau social est le plus important aura une centralité de proximité plus élevée qu’un utilisateur connecté via d’autres personnes (en d’autres termes, un ami d’un ami).
Remarque :
La distance entre les nœuds désigne le nombre de liens qui les séparent, et non la distance géographique.
La centralité de proximité du nœud x est calculée à l’aide de l’équation suivante :
closeCentrality(x)=(nodes(x,y)/(NodesTotal-1))*(nodes(x,y)/dist(x,y)Total)où :
- NodesTotal = nombre de nœuds dans le réseau
- nodes(x,y) = nombre de nœuds connectés au nœud x
- dist(x,y)Total = somme des distances du plus court chemin entre le nœud x et d’autres nœuds
Centralité de vecteur propre
La centralité de vecteur propre repose sur des nœuds importants connectés à d’autres nœuds importants. Vous devez l’utiliser pour identifier les nœuds qui font partie d’un agrégat influent. Par exemple, un utilisateur d’un réseau social connecté à de nombreux autres utilisateurs, eux-mêmes connectés à de nombreux autres utilisateurs, bénéficiera d’une centralité de vecteur propre plus élevée qu’un utilisateur connecté à un petit nombre d’utilisateurs, ou qui est connecté à des utilisateurs eux-mêmes connectés à peu d’utilisateurs.
La centralité de vecteur propre du nœud x se calcule à l’aide d’une itération de puissance afin de trouver le vecteur propre le plus grand avec l’équation suivante :
Ax=λxoù :
- λ = valeur propre
- x = vecteur propre
- A = matrice décrivant la transformation linéaire
Pondération de tronçon
Les calculs d’intermédiarité, de proximité et de centralité de vecteur propre peuvent être pondérés ou non pondérés. Un calcul de centralité non pondéré définit les tronçons sur une pondération uniforme avec une valeur de 1, tandis qu’un calcul pondéré utilise des valeurs de champ pour attribuer une valeur à chaque tronçon.
Remarque :
Les pondérations non définies reçoivent une valeur de 1. Il est recommandé d’attribuer un champ sans valeurs nulles ou manquantes pour la pondération de tronçon.
Pour la centralité de vecteur propre, les pondérations sont utilisées afin de déterminer la force de la connexion entre les nœuds. Puisque la centralité de vecteur propre mesure l’importance des nœuds dans le réseau, les valeurs de pondérations plus élevées correspondent aux valeurs plus élevées liées à leurs nœuds de connexion.
Pour les centralités d’intermédiarité et de proximité, les valeurs de pondération indiquent la distance entre les nœuds. Les pondérations de tronçon plus élevées indiquent une distance plus grande entre les nœuds et réduisent la probabilité que le tronçon soit utilisé dans le chemin le plus court. Si un nombre plus élevé dans le champ de pondération désiré indique une importance accrue (par exemple, le nombre de messages envoyés entre des membres d’un réseau social indique comment ces membres sont connectés), un nouveau champ doit être calculé avec des valeurs inverses. Utilisez l’équation suivante pour calculer un champ de valeurs inverses :
weight=ABS(field-MAX(field))+IF(MIN(field)<0, ABS(MIN(field)), MIN(field))Pour un calcul de proximité ou d’intermédiarité non pondéré, le chemin le plus court est celui qui utilise le moins de liens. L’exemple ci-dessous présente un réseau comportant quatre nœuds (A, B, C et D) et des pondérations uniformes. Deux chemins joignent le nœud A au nœud D : A-B-D ou A-B-C-D. Puisque A-B-D comporte moins de liens, il s’agit du chemin le plus court.

Un calcul pondéré applique des pondérations à chaque tronçon en fonction de valeurs de champ. Les centralités d’intermédiarité et de proximité pondérées utilisent l’algorithme de Bellman-Ford pour trouver les chemins les plus courts entre les nœuds.
L’exemple ci-dessous présente un réseau comportant quatre nœuds et des tronçons pondérés. Le chemin A-B-D possède la valeur 15 et le chemin A-B-C-D la valeur 9. Le chemin A-B-C-D ayant la valeur de tronçon la plus faible, il s’agit du chemin le plus court.
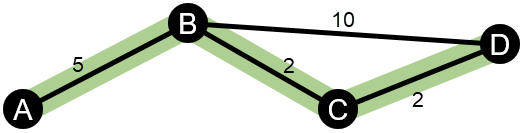
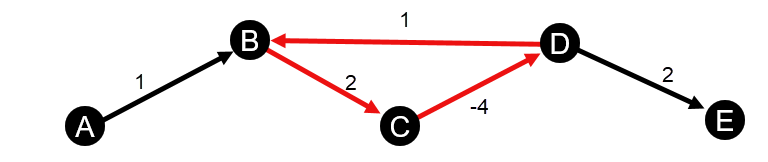
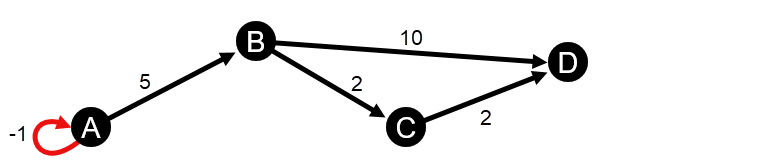
Les calculs de centralité de proximité et d’intermédiarité pondérés ne prennent pas en charge les cycles de pondération négatifs. Si un cycle de pondération négatif est détecté, toutes les valeurs de centralité sont définies sur 0. Un cycle de pondération négatif survenir dans les circonstances suivantes :
- Le diagramme contient un cycle négatif.
- Le diagramme contient une boucle négative.
- Le diagramme est non directionnel et contient un tronçon négatif.
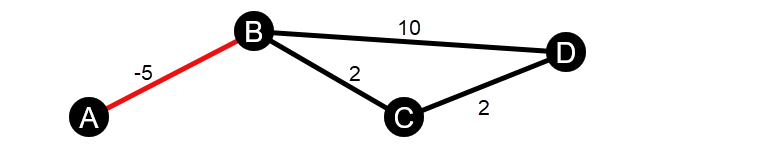
Etapes suivantes
Essayez ces exercices à scénario disponibles sur Apprendre à utiliser ArcGIS pour des processus guidés avec une analyse de liens :
Vous avez un commentaire à formuler concernant cette rubrique ?