Pourquoi des hexagones ?

L'agrégation des données ponctuelles d'incident en grilles de forme régulière est utilisée dans de nombreux cas, notamment pour normaliser la géographie de la cartographie ou pour atténuer les problèmes liés à l'utilisation de polygones de forme irrégulière créés arbitrairement (par exemples, des limites de comtés ou des groupes d'îlots qui ont été créés à partir d'un processus politique). Les grilles de forme régulière peuvent uniquement se composer de triangles équilatéraux, de carrés ou d'hexagones, car ces trois formes de polygones sont les seules à pouvoir être tessellées (répétition de la même forme, de tronçon à tronçon, pour couvrir une surface sans interruption ou superposition) en vue de créer une grille espacée régulièrement.

Même si la grille carrée (quadrillage) est le type de forme le plus couramment utilisé dans l'analyse SIG et la cartographie thématique, il peut arriver que les hexagones soient mieux adaptés à votre analyse en fonction de la nature de votre question.

Voici les raisons pour lesquelles vous pouvez envisager l'agrégation en grille hexagonale :

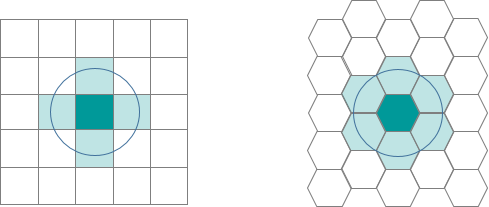
• Les hexagones réduisent les déformations d'échantillonnage provoquées par les effets de tronçon de la forme de la grille. Ceci est lié au rapport périmètre-surface faible de la forme de l'hexagone. Un cercle dispose du rapport le plus faible, mais ne peut pas être tessellé pour constituer une grille continue. Les hexagones sont les polygones dont la forme est la plus circulaire pouvant être tessellés pour constituer une grille espacée régulièrement.
• Le caractère circulaire d'une grille hexagonale lui permet de représenter plus naturellement les courbes des modèles de vos données que les grilles carrées.
• Lorsque vous comparez des polygones de surfaces égales, plus le polygone est semblable à un cercle et plus les points à proximité de la bordure sont proches du centroïde (tout particulièrement les points à proximité des sommets). Cela signifie que les points situés au sein d'un hexagone sont plus proches du centroïde de l'hexagone que n'importe quel point donné dans un carré ou un triangle de surface égale (ceci s'explique par les angles plus aigus du carré et du triangle par rapport à l'hexagone).
• Les hexagones sont préférables lorsque votre analyse comprend des aspects de connectivité ou des chemins de déplacement.
• En raison de la nature linéaire des rectangles, les quadrillages peuvent attirer notre attention sur les lignes droites, continues et parallèles qui risquent de gêner les modèles sous-jacents des données. Les hexagones ont tendance à décomposer les lignes et permettent de voir plus clairement et facilement la courbure des modèles dans les données. Cette décomposition des modèles linéaires artificiels réduit par ailleurs les déformations d'orientation qui peuvent être perçues dans les quadrillages.
• Si vous utilisez une surface importante, un hexagone subira une distorsion moindre grâce à la courbure de la Terre que la forme d'un quadrillage.
• La recherche de voisins est plus simple avec une grille hexagonale. Comme le tronçon ou la longueur de contact est identique sur chaque côté, le centroïde de chaque voisin est équidistant. Toutefois, avec un quadrillage, les centroïdes des voisins Rook's Case (dessus/dessous/droite/gauche) sont éloignés de N unités, tandis que les centroïdes des voisins diagonaux (Queen) sont plus éloignés (exactement de la racine carrée de 2 fois N unités).
• Comme la distance entre les centroïdes est identique dans les six directions avec les hexagones, si vous utilisez une bande de distance pour rechercher les voisins ou utilisez l’outil Analyse de points chauds optimisée, Analyse de points aberrants optimisée ou Créer un cube spatio-temporel en agrégeant des points, davantage de voisins sont inclus dans les calculs pour chaque entité si vous utilisez une grille hexagonale au lieu d’un quadrillage.

  

Ressources supplémentaires :

Birch, Colin P.D., Oom, Sander P., and Beecham, Jonathan A. Rectangular and hexagonal grids used for observation, experiment, and simulation in ecology. Ecological Modelling, Vol. 206, No. 3–4. (August 2007), pp. 347–359.