Cet outil calcule la régression pondérée géographiquement, formule locale de régression utilisée pour modéliser des relations variant spatialement. L’outil GWR offre un modèle local de la variable ou du processus que vous tentez de comprendre ou de prévoir en ajustant une équation de régression à chaque entité du jeu de données. L’outil GWR crée ces équations distinctes en insérant les variables dépendantes et explicatives des entités se trouvant dans le voisinage de chaque entité cible. La forme et l’étendue de chaque voisinage analysé dépendent de l’entrée des paramètres Neighborhood Type (Type de voisinage) et Neighborhood Selection Method (Méthode de sélection de voisinage) . Il existe néanmoins une restriction : lorsque le nombre d’entités voisines dépasse 1 000, seules les 1 000 entités les plus proches sont incorporées dans chaque équation locale.
Pour obtenir des résultats optimaux, appliquez cet outil aux jeux de données contenant plusieurs centaines d’entités. Cet outil ne convient pas aux petits jeux de données. L'outil ne fonctionne pas avec les données multi-points.
Utilisez le paramètre Entités en entrée avec un champ représentant les phénomènes que vous modélisez (valeur Variable dépendante) et un ou plusieurs champs représentant la valeur Variables explicatives. Ces champs doivent être numériques et comporter une plage de valeurs. Les entités qui comportent des valeurs manquantes dans la variable dépendante ou explicative seront exclues de l’analyse. Vous pouvez toutefois utiliser l’outil Renseigner les valeurs manquantes pour renseigner le jeu de données avant d’exécuter l’outil GWR.
L’outil GWR génère différents résultats en sortie. Un résumé du modèle de régression pondérée géographiquement est disponible sous forme de message au bas de la fenêtre Géotraitement lors de l’exécution de l’outil. Pour accéder au message, passez le curseur de la souris sur la barre de progression et cliquez sur le bouton de menu contextuel ou développez la section des messages dans la fenêtre Géotraitement. Vous pouvez également accéder aux messages d’un outil GWR précédemment exécuté via l’historique du géotraitement.
L’outil accepte les points et les polygones comme entrée. Pour les polygones, toutes les distances et tous les voisins sont déterminés à l’aide de la distance entre les centroïdes de polygones (points). Néanmoins, un seul point ne saurait constituer une bonne représentation du polygone, en particulier pour les grands polygones, les polygones allongés ou les polygones multi-parties. Dans ces cas, les voisins et les distances entre les polygones peuvent être peu intuitifs ou trompeurs. Par exemple, deux polygones qui partagent une limite peuvent ne pas être considérés comme voisins si leurs centroïdes sont éloignés. Pour voir les centroïdes utilisés par cet outil, utilisez l’outil Feature To Point (Entité vers point) avec le paramètre Inside (Intérieur) décoché pour convertir les polygones en points centroïdes. Vous pouvez également utiliser l’explorateur de voisinage pour visualiser les voisins des polygones ou les centroïdes.
En règle générale, il n’est pas recommandé d’utiliser la régression pondérée géographiquement sur les lignes, car un centroïde est rarement une représentation appropriée d’une ligne. Cependant, pour utiliser les lignes dans l’outil, vous pouvez utiliser l’outil Feature To Point (Entité vers point) pour convertir les lignes en points centroïdes et utiliser les centroïdes dans l’outil. Les résultats peuvent alors être joints à nouveau aux lignes d’origine.
La valeur du paramètre Model Type (Type de modèle) spécifiée dépend des données que vous modélisez. Il est important d’utiliser le modèle approprié pour l’analyse afin d’obtenir des résultats exacts de l’analyse de régression.
Il est recommandé d’utiliser des données projetées. Ceci est particulièrement important lorsque la distance est un composant de l’analyse, comme c’est le cas pour la régression pondérée géographiquement lorsque vous spécifiez Bande de distance pour le paramètre Type de voisinage. Il est recommandé de projeter les données à l’aide d’un système de coordonnées projetées (et non avec un système de coordonnées géographiques).
Certains calculs peuvent utiliser plusieurs unités centrales de traitement pour augmenter la performance et utilisent automatiquement jusqu’à huit threads/unités centrales de traitement.
Il est courant d’explorer les données globalement à l’aide de l’outil Generalized Linear Regression (Régression linéaire généralisée) avant de les explorer localement avec cet outil.
Les paramètres Variable dépendante et Variables explicatives doivent être des champs numériques contenant différentes valeurs. Ces valeurs doivent présenter une variation, à la fois globalement et localement. C’est pour cela que vous ne devez pas utiliser de variables explicatives fictives pour représenter différents régimes spatiaux dans le modèle de régression pondérée géographiquement (en affectant par exemple la valeur 1 aux secteurs de recensement situés à l’extérieur du noyau urbain, tandis que tous les autres ont la valeur 0). Étant donné que l’outil Régression pondérée géographiquement permet aux coefficients variables explicatifs de varier, ces variables explicatives de régime spatial sont inutiles, et si elles sont incluses, elles sont susceptibles de créer des problèmes de multicolinéarité locale.
Dans les modèles de régression globaux, tels que Generalized Linear Regression (Régression linéaire généralisée), les résultats sont peu fiables si plusieurs variables présentent une multicolinéarité (lorsque plusieurs variables sont redondantes ou racontent la même histoire). L’outil Régression pondérée géographiquement génère une équation de régression locale pour chaque entité dans le jeu de données. Si les valeurs d’une variable explicative particulière s’agrègent spatialement, vous risquez de rencontrer des problèmes de multicolinéarité locale. Le champ de conditionnement (COND) dans la classe d’entités en sortie indique quand les résultats sont instables en raison d’un problème de multicolinéarité local. En règle générale, soyez critique à l’égard des résultats d’entités présentant un conditionnement supérieur à 30, nul ou, pour les shapefiles, égal à -1.7976931348623158e+308. Le numéro de condition est ajusté à l’échelle pour corriger le nombre de variables explicatives dans le modèle. Cela permet de comparer directement le numéro de condition entre les modèles utilisant des nombres de variables explicatives différents.
Soyez prudent lorsque vous incluez des données nominales ou catégorielles dans un modèle de régression pondérée géographiquement. Lorsque les catégories s’agrègent spatialement, vous risquez de rencontrer des problèmes de multicolinéarité locale. Le numéro de condition compris dans la sortie de la régression pondérée géographiquement (GWR) indique quand la colinéarité locale présente un problème (numéro de condition inférieur à 0, supérieur à 30, ou défini sur nul). En présence de multicolinéarité locale, les résultats sont instables.
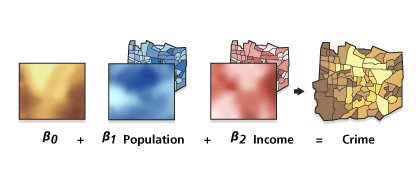
Pour mieux comprendre la notion de variation régionale parmi les coefficients de variables explicatives, examinez les surfaces de coefficient raster facultatives créées par l’outil GWR. Ces surfaces raster sont créées dans le paramètre Coefficient Raster Workspace (Espace de travail raster du coefficient) sous Additional Options (Options supplémentaires), si spécifié. Pour les données surfaciques, vous pouvez utiliser des couleurs graduées ou un rendu de tonalités froides à chaudes pour chaque champ de coefficient dans Entités en sortie afin d’examiner les modifications survenues dans la zone d’étude.
Vous pouvez utiliser l’outil GWR pour une prévision en fournissant une valeur Prediction Locations (Localisations des prévisions) (cette classe d’entités est souvent la même que la valeur Input Features (Entités en entrée)), en appariant les variables explicatives et en spécifiant une valeur Output Predicted Features (Entités prévues en sortie). Si les champs Variables explicatives à apparier de la valeur Entités en entrée correspondent aux champs Champs issus des localisations des prévisions, ils sont automatiquement renseignés. Sinon, spécifiez les champs appropriés.
Un modèle de régression est incorrectement spécifié s’il manque une variable explicative clé. Une autocorrélation spatiale statistiquement significative des résidus de régression ou une variation spatiale inattendue parmi les coefficients d’une ou de plusieurs variables explicatives indique que le modèle est incorrectement spécifié. Faites tout pour découvrir (via l’analyse des résiduels du modèle de régression linéaire généralisée et l’analyse de la variation des coefficients du modèle de régression pondérée géographiquement, par exemple) ces variables manquantes clés afin de pouvoir les inclure dans le modèle.
Déterminez la pertinence de la nature non stationnaire d’une variable explicative. Par exemple, supposons que vous modélisiez la densité d'une espèce de plante particulière en tant que fonction de plusieurs variables, notamment ASPECT (exposition). Si le coefficient varie pour la variable ASPECT dans la zone d’étude, c’est vraisemblablement qu’il manque une variable explicative clé (la prédominance de la végétation concurrente, par exemple). Faites en sorte d’inclure toutes les variables explicatives clés dans le modèle de régression.
Lorsque le résultat d’un calcul est l’infini ou indéfini, le résultat pour les fichiers qui ne sont pas des shapefiles sera nul ; pour les shapefiles, le résultat sera - DBL_MAX = -1.7976931348623158e+308.
Attention :
Les fichiers de formes ne peuvent pas stocker de valeurs nulles. Les outils ou autres procédures qui créent des shapefiles à partir d’entrées dans d’autres formats peuvent stocker des valeurs nulles, comme zéro ou un nombre négatif très petit (- DBL_MAX = -1.7976931348623158e+308). Cela peut aboutir à des résultats inattendus. Pour plus d’informations, reportez-vous à la rubrique Remarques concernant le géotraitement pour la sortie de shapefiles.
Trois options sont disponibles pour le paramètre Neighborhood Selection Method (Méthode de sélection de voisinage). Lorsque vous indiquez Golden search (Recherche absolue), l’outil recherche les valeurs les mieux adaptées au paramètre Distance Band (Bande de distance) ou Number of Neighbors (Nombre de voisins) à l’aide de la méthode de recherche absolue. L’option Manual intervals (Intervalles manuels) teste les voisins par incréments entre les distances spécifiées. Dans tous les cas, la taille utilisée pour les voisins est celle qui minimise la valeur du critère d'information Akaike (AICc). Toutefois, les problèmes de multicolinéarité locale empêcheront ces deux méthodes de trouver un canal de distance ou un nombre de voisins optimaux. Si vous rencontrez une erreur ou de graves problèmes de conception de modèle, vous pouvez spécifier une distance ou un nombre de voisins en particulier à l’aide de l’option User defined (Définir par l’utilisateur). Examinez ensuite les conditionnements dans la classe d’entités en sortie pour déterminer quelles entités sont associées à des problèmes de colinéarité locale.
Les problèmes graves de conception de modèle ou les erreurs indiquant que les équations that locales ne comprennent pas assez de voisins, signalent souvent un problème de multicolinéarité globale ou locale. Pour déterminer l’origine du problème, exécutez un modèle global à l’aide de l’outil Régression linéaire généralisée et examinez la valeur VIF de chaque variable explicative. Si certaines valeurs VIF sont élevées (supérieures à 7,5, par exemple), la multicolinéarité globale empêche la résolution de la régression pondérée géographiquement. Toutefois, la multicolinéarité locale est plus vraisemblablement à l'origine du problème. Essayez de créer une carte thématique pour chaque variable explicative. Si la carte révèle une agrégation spatiale de valeurs identiques, envisagez la suppression de ces variables du modèle ou leur combinaison avec d’autres variables explicatives afin d’augmenter la variation des valeurs. Par exemple, si vous modélisez des valeurs d’habitat et que vous disposez de variables pour les chambres et les salles de bains, vous pouvez les combiner pour augmenter la variation des valeurs ou les représenter en tant que superficie de salle de bain/chambre. Évitez d'utiliser des variables fictives de régime spatial, des variables catégorielles/nominales spatialement agrégées ou des variables avec très peu de valeurs possibles, lorsque vous créez des modèles de régression pondérée géographiquement.
Le modèle de régression pondérée géographiquement est un modèle linéaire soumis aux mêmes conditions requises que l’outil Generalized Linear Regression (Régression linéaire généralisée). Examinez les diagnostics expliqués dans la rubrique Fonctionnement de l’outil Régression pondérée géographiquement pour vérifier que votre modèle de régression pondérée géographiquement est correctement spécifié. La section Corruption des modèles de régression de la rubrique Principes de base de l’analyse de régression explique également comment s’assurer de l’exactitude du modèle.