L’outil Régression pondérée géographiquement utilise une régression pondérée géographiquement qui est l’une des techniques de régression spatiale utilisées en géographie et dans d’autres disciplines. Elle évalue un modèle local de la variable ou du processus que vous essayez de comprendre ou de prévoir en ajustant une équation de régression à chaque entité du jeu de données. La régression pondérée géographiquement crée ces équations distinctes en insérant les variables dépendantes et explicatives des entités se trouvant dans le voisinage de chaque entité cible. Lorsque vous utilisez l’outil Régression pondérée géographiquement, la forme et l’étendue de chaque voisinage analysé repose sur les paramètres Type de voisinage et Méthode de sélection des voisins. L’outil autorise des données continues (gaussiennes), binaires (logistiques) ou totales (Poisson) comme variable dépendante. Utilisez la régression pondérée géographiquement avec plusieurs centaines d’entités au moins.
Remarque :
L’outil Régression pondérée géographiquement multi-échelle permet de réaliser une régression pondérée géographiquement sur des données à différentes échelles de relations entre les variables dépendantes et explicatives.
Applications possibles
L’outil Régression pondérée géographiquement permet de répondre à une multitude de questions et notamment aux suivantes :
- La relation entre niveau de diplôme et revenu est-elle cohérente à travers la zone d’étude ?
- Les incidences de certaines maladies augmentent-elles avec la proximité par rapport aux entités d'eau ?
- Quelles sont les variables clés qui expliquent la fréquence élevée d'incendies de forêt ?
- Quels habitats devraient être protégés pour favoriser la réintroduction d'une espèce en danger ?
- Dans quels arrondissements/quartiers les enfants obtiennent-ils des résultats élevés aux examens ? Quelles caractéristiques semblent être associées ? Où chacune des caractéristiques est-elle la plus importante ?
- Les facteurs influencent-ils des taux de cancer plus élevés de manière cohérente à l’échelle de la zone d'étude ?
Entrées
Pour exécuter l’outil Régression pondérée géographiquement, spécifiez le paramètre Entités en entrée, avec un champ représentant la variable dépendante et un ou plusieurs champs représentant la ou les variables explicatives. Ces champs doivent être numériques et comporter une plage de valeurs. Les entités qui comportent des valeurs manquantes dans la variable dépendante ou explicative seront exclues de l’analyse. Vous pouvez toutefois utiliser l’outil Renseigner les valeurs manquantes pour renseigner le jeu de données avant d’exécuter l’outil Régression pondérée géographiquement. Choisissez ensuite un type de modèle en fonction des données que vous analysez. Il est important d’utiliser un modèle adapté aux données. Les types de modèles et comment déterminer le modèle adapté à vos données sont présentés ci-dessous.
Types de modèle
L’outil Régression pondérée géographiquement propose trois types de modèle de régression : continu, binaire et total. Ces types de régression sont appelés moindres carrés ordinaires, logistique et Poisson respectivement. Basez la valeur du paramètre Type de modèle de l’analyse sur la façon dont la variable dépendante a été mesurée ou synthétisée ainsi que sur la plage de valeurs qu’il contient.
Continu (gaussien)
Utilisez l’option Continu (gaussien) si la variable dépendante peut adopter une plage de valeurs étendue, comme la température ou un volume total de ventes. Il est recommandé que la variable dépendante soit distribuée normalement. Vous pouvez créer un histogramme de la variable dépendante pour vérifier qu’elle est distribuée normalement. Si l’histogramme présente une courbe en cloche symétrique, utilisez un type de modèle gaussien. La plupart des valeurs sont généralement concentrées près de la moyenne, peu de valeurs s’en écartant radicalement. Il devrait y avoir autant de valeurs du côté gauche de la moyenne que du côté droit (valeurs moyennes et médianes de la distribution sont les mêmes). Si la variable dépendante ne semble pas être distribuée normalement, envisagez de la reclasser en variable binaire. Par exemple, si la variable dépendante est le revenu moyen des ménages, vous pouvez la recoder en variable binaire, 1 indiquant un revenu supérieur à la moyenne nationale et 0 (zéro), un revenu inférieur à la moyenne nationale. Vous pouvez reclasser un champ continu en champ binaire en utilisant la fonction d’aide Reclassification dans l’outil Calculer un champ.
Binaire (logistique)
Utilisez l’option Binaire (logistique) si la variable dépendante peut adopter l’une des deux valeurs possibles, telles que réussite ou échec, ou présence ou absence. Le champ contenant la variable dépendante doit être un champ numérique et ne contenir que des uns et des zéros. Les résultats seront plus faciles à interpréter si vous codez l’événement présentant un intérêt, comme la réussite ou la présence d’un animal, avec la valeur 1, puisque la régression modélisera la probabilité de 1. Les données doivent présenter une variation des valeurs un et zéro à la fois globalement et localement. Vous pouvez utiliser l’outil Résumés statistiques de voisinage pour calculer les écarts types des voisinages locaux afin de localiser les zones contenant toutes la même valeur.
Total (Poisson)
Utilisez l’option Total (Poisson) si la variable dépendante est discrète et représente le nombre d’occurrences d’un événement, tel que le nombre de délits. Les modèles de type Total peuvent également être utilisés si la variable dépendante représente un taux et que le dénominateur du taux est une valeur fixe telle que les ventes par mois ou le nombre de personnes atteintes de cancer parmi un échantillon de 10 000 personnes. Les valeurs de la variable dépendante ne peuvent pas être négatives ni contenir de décimales.
Types de voisinage
Un voisinage est la bande de distance ou le nombre de voisins utilisés pour chaque équation de régression locale et peut-être le paramètre le plus important à prendre en compte pour l’outil Régression pondérée géographiquement, puisque c’est ce qui contrôle la façon dont les modèles sont estimés. La forme et l’étendue de chaque voisinage analysé repose sur les valeurs des paramètres Type de voisinage et Méthode de sélection des voisins.
Vous pouvez choisir l’un des deux types de voisinage : un nombre fixe de voisins ou une bande de distance. Pour un nombre fixe de voisins, la zone de chaque voisinage dépend de la densité des points à proximité : les voisinages sont plus petits lorsque les entités sont denses et plus grands lorsque les entités sont clairsemées. Lorsque la bande de distance est utilisée, la taille du voisinage reste constante pour chaque entité de la zone d’étude, ce qui se traduit par un nombre d’entités par voisinage plus élevé là où la densité des entités est importante et un nombre d’entités par voisinage plus faible lorsque les entités sont clairsemées.
La méthode de sélection des voisins spécifie la façon dont est déterminée la taille du voisinage (la distance ou le nombre de voisins effectivement utilisé). Les voisinages sélectionnés à l’aide de l’option Recherche absolue ou Intervalles manuels supposent de réduire la valeur du critère d'information Akaike (AICc). Une autre possibilité, consiste à définir une distance de voisinage spécifique ou un nombre de voisins déterminé à l'aide de l’option Défini par l’utilisateur.
Dans le cas de la méthode de sélection Recherche absolue, l’outil détermine les valeurs les mieux adaptées à la bande de distance ou au nombre de voisins à l’aide de la méthode de recherche absolue. Cette méthode identifie tout d’abord les distances maximale et minimale et teste l’AICc à diverses distances en procédant par incrémentation. La distance maximale est celle à laquelle chaque entité possède la moitié des entités en entrée comme voisins, et la distance minimale est celle à laquelle chaque entité compte au minimum 5 pour cent des entités du jeu de données comme voisins.
Les paramètres Distance de recherche minimale et Distance de recherche maximale (pour la bande de distance) et Nombre minimal de voisins et Nombre maximal de voisins (pour le nombre de voisins) peuvent être utilisés pour restreindre la plage de recherche de la recherche absolue.
Remarque :
Si les paramètres de voisinage renvoient plus de 1 000 voisins pour un voisinage, seuls les 1 000 voisins les plus proches sont utilisés.
Structure de pondération locale
La régression pondérée géographiquement a pour avantage d’appliquer une pondération géographique aux entités utilisées dans chacune des équations de régression locales. Une pondération moins importante est attribuée aux entités les plus éloignées des points de régression, celles-ci ont moins d’influence sur les résultats de régression pour l’entité cible ; les entités plus proches ont une pondération plus importante dans l’équation de régression. Les pondérations sont déterminées à l’aide d’un noyau. Un noyau est une fonction qui détermine à quelle vitesse les pondérations diminuent à mesure que les distances augmentent. L’outil Régression pondérée géographiquement propose deux options de noyau pour le paramètre Structure de pondération locale : Gaussien et Bicarré.
La structure de pondération gaussienne attribue une pondération égale à un à l’entité focale et des pondérations aux entités environnantes diminuant de manière progressive à mesure qu’augmente la distance par rapport à l’entité focale. Par exemple, si les deux entités sont situées à une distance de 0,25 bande passante l’une de l’autre, la pondération obtenue par l’équation sera approximativement de 0,88. Si les entités sont situées à une distance de 0,75 bande passante l’une de l’autre, la pondération obtenue sera approximativement de 0,32. Une structure de pondération Gaussian (Gaussienne) n’atteint jamais la valeur zéro, mais les pondérations des entités éloignées de l’entité de régression peuvent être très faibles et n’avoir presque aucun impact sur la régression. Lorsqu’on utilise une structure de pondération gaussienne, toutes les autres entités des données en entrée sont des entités voisines et se voient attribuer une pondération. Toutefois, pour garantir l’efficacité des calculs, lorsque le nombre d’entités voisines dépasse 1 000, seules les 1 000 entités les plus proches sont intégrées à chaque régression locale. Une structure de pondération gaussienne garantit un grand nombre de voisins pour chaque entité de régression, ce qui augmente la probabilité d’une variation dans les valeurs de ces voisins. Ce qui évite les problèmes courants de colinéarité locale en termes de régression pondérée géographiquement. Utilisez une structure de pondération de type Gaussien lorsque l’influence des entités voisines devient progressivement moins importante mais que cette influence reste présente peu importe le degré d’éloignement des entités environnantes.
La structure de pondération bicarrée est similaire à la fonction gaussienne. Elle attribue une pondération égale à un à l’entité focale et des pondérations aux entités environnantes diminuant de manière progressive à mesure qu’augmente la distance par rapport à l’entité focale. Toutefois, toutes les entités se trouvant en dehors du voisinage spécifié se voient attribuer la valeur zéro et n’ont pas d’influence sur la régression locale pour l’entité cible. Lorsque l’on compare une structure de pondération bicarrée à une structure de pondération gaussienne en utilisant les mêmes spécifications de voisinage, les pondérations diminuent plus rapidement avec la méthode bicarrée. L’utilisation d’une structure de pondération bicarrée vous permet de spécifier une distance au-delà de laquelle les entités n’ont plus d’impact sur les résultats de régression. Puisque la méthode bicarrée exclut les entités au-delà d’une certaine distance, il n’y a pas de garantie que le nombre d’entités (avec influence) est suffisant dans le voisinage immédiat pour produire une analyse de régression locale significative. Utilisez une structure de pondération gaussienne lorsque l’influence des entités voisines diminue progressivement et qu’il existe une distance au-delà de laquelle cette influence n’existe plus. Par exemple, la régression est fréquemment utilisée pour modéliser le prix de l'immobilier, le prix de vente des logements environnants étant une variable explicative habituelle. Les logements environnants sont nommés propriétés comparables. Les organismes de prêts déterminent parfois une distance maximum entre logements comparables. Dans cet exemple, une structure de pondération bicarrée peut être utilisée avec un voisinage correspondant à la distance maximale spécifiée par l’organisme de prêts.
Prévision
Vous pouvez utiliser le modèle de régression créé pour effectuer des prévisions pour d’autres entités (ponctuelles ou surfaciques) dans la même zone d’étude en fournissant les entités dans le paramètre Localisations des prévisions. Les localisations des prévisions doivent avoir des champs correspondants pour chaque variable explicative dans les entités en entrée. Si les noms des champs des entités en entrée et des localisations des prévisions ne concordent pas, vous devez apparier les champs correspondants dans le paramètre Variables explicatives à apparier. Lors de l’appariement, les champs doivent être du même type (les champs doubles ne peuvent pas être appariés à des champs de type entier, par exemple).
Rasters de coefficient
L’avantage principal de la régression pondérée géographiquement par rapport à la plupart des modèles de régression est la possibilité d’explorer spatialement différentes relations. Une façon de visualiser dans l’espace la variation des relations entre les variables explicatives et la variable dépendante est de créer des rasters de coefficient. Lorsque vous indiquez un nom de chemin d’accès comme valeur du paramètre Espace de travail raster du coefficient, l’outil Régression pondérée géographiquement crée des surfaces raster de coefficient pour l’intersection du modèle et chaque variable explicative. La résolution des rasters peut être contrôlée à l'aide du paramètre d'environnement Cell Size (Taille de cellule). Un voisinage est construit autour de chaque cellule raster selon le type de voisinage et de la structure de pondération. Les pondérations sont calculées à partir du centre de la cellule raster vers toutes les entités en entrée se trouvant dans la zone de voisinage. Ces pondérations permettent de calculer une équation de régression unique pour cette cellule raster. Les coefficients varient d’une cellule raster à une autre puisque les voisins et les pondérations changent d’une cellule à l’autre.
Remarque :
Il n’existe à l’heure actuelle aucun consensus sur la façon d’évaluer le degré de confiance des coefficients d’un modèle de régression pondérée géographiquement. Si des tests t ont été effectués afin de déduire si la valeur estimée des coefficients est considérablement différente de zéro, la validité de cette approche fait toujours l’objet de recherches. Une approche simple pour évaluer les coefficients consiste à diviser le coefficient par l’erreur standard fournie pour chaque entité afin de mesurer l’ampleur de l’estimation à l’aide de l’erreur standard associée et de visualiser ces résultats, en recherchant les agrégats élevés d’erreurs standard liées au coefficient.
Sorties
L’outil Régression pondérée géographiquement produit diverses sorties. Un résumé du modèle de régression pondérée géographiquement, ainsi que des résumés statistiques, sont renvoyés sous forme de messages. L’outil génère également une classe d’entités en sortie, des diagrammes ainsi que, éventuellement, des entités de prévision et des surfaces raster de coefficient. Les entités en sortie et les diagrammes associés sont automatiquement ajoutés à la fenêtre Contenu et un schéma de rendu chaud et froid est appliqué aux valeurs résiduelles du modèle. Les diagnostics et diagrammes générés dépendent du type de modèle spécifié.
Continu (gaussien)
Le type de modèle gaussien suppose que les valeurs de la variable dépendante sont continues.
Entités en sortie
Outre les valeurs résiduelles de régression, les entités en sortie comprennent les champs des valeurs des variables dépendantes observées et prévues, l’indice de conditionnement, la valeur R-carré locale, les coefficients des variables explicatives et les erreurs standards. Sur une carte, les entités en sortie sont ajoutées sous forme d'une couche et symbolisées par les valeurs résiduelles normalisées. Une valeur résiduelle normalisée positive signifie que la variable dépendante est supérieure à la valeur prédite (sous-estimation) et une valeur résiduelle normalisée négative signifie que la variable dépendante est inférieure à la valeur prédite (surestimation)
L’interception, l’erreur standard de l’interception, les coefficients, les erreurs standard pour chaque variable explicative, ainsi que les valeurs prévues, résiduelles, résiduelles standards, l’influence, la valeur Cook’s D, la valeur R-carré locale et l’indice de conditionnement sont également indiquées. Nombre de ces champs sont abordés à la rubrique Fonctionnement de la régression des moindres carrés ordinaires. Les valeurs Influence et Cook's D mesurent toutes les deux l’influence de l’entité dans l’estimation des coefficients de régression. Vous pouvez utiliser un histogramme pour déterminer si certaines entités ont plus d’influence que le reste du jeu de données. Ces entités sont souvent des points aberrants qui déforment l’estimation des coefficients. Pour améliorer les résultats du modèle, il peut être judicieux de les supprimer et de relancer l’outil. La valeur de R-carré locale est comprise entre 0 et 1. Elle représente la force des corrélations du modèle local de l’entité. L’indice de conditionnement est une mesure de la stabilité des coefficients estimés. Les indices de conditionnement supérieurs à environ 1 000 indiquent l’instabilité du modèle. Cela est généralement le fait de variables explicatives fortement corrélées les unes aux autres.
Interpréter des messages et diagnostics
Les détails d’analyse sont fournis dans les messages et incluent le nombre d’entités analysées, les variables dépendantes et explicatives, et le nombre de voisins spécifié. En outre, différents diagnostics de modèle sont signalés.
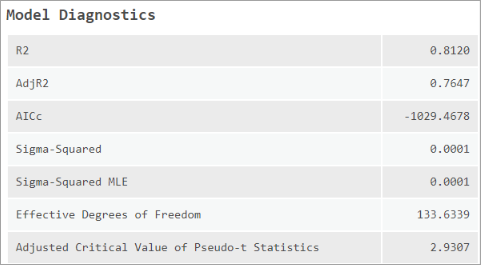
- R2 : R au carré est une mesure de la qualité d'ajustement. Sa valeur varie de 0,0 à 1,0, les valeurs supérieures étant préférables. Elle peut être interprétée en tant que proportion de variance de la variable dépendante correspondant au modèle de régression. Le dénominateur pour le calcul de R2 est la somme des valeurs de variables dépendantes au carré. L'ajout d'une variable explicative supplémentaire au modèle ne modifie pas le dénominateur mais le numérateur ; ce qui donne une impression d'amélioration dans l'ajustement du modèle qui peut ne pas être réelle. Voir AdjR2 ci-dessous.
- R2 ajusté : en raison du problème décrit ci-dessus pour la valeur R2, les calculs pour la valeur R-carré ajustée normalisent le numérateur et le dénominateur par leurs degrés de liberté. Cela a pour effet de compenser le nombre de variables d’un modèle ; par conséquent, la valeur R2 ajustée est presque toujours inférieure à la valeur R2. Toutefois, pour effectuer cet ajustement, vous perdez l'interprétation de la valeur en tant que proportion de la variance expliquée. Dans la régression pondérée géographiquement, le nombre effectif de degrés de liberté étant une fonction du voisinage utilisé, l’ajustement peut donc être marqué par rapport à un modèle global comme celui utilisé par l’outil Régression linéaire généralisée. Pour cette raison, il est préférable d’utiliser la valeur AICc pour comparer des modèles.
- AICc : mesure des performances du modèle, utile pour comparer des modèles de régression. En considérant la complexité du modèle, un modèle de valeur AICc inférieure fournit un meilleur ajustement aux données observées. La valeur AICc n'est pas une mesure absolue de la qualité d'ajustement mais elle est utile pour la comparaison de modèles avec des variables explicatives différentes, tant qu'ils s'appliquent à la même variable dépendante. Si les valeurs AICc de deux modèles diffèrent de plus de 3, le modèle avec la valeur AICc inférieure est considéré comme meilleur. La comparaison de la valeur AICc de régression pondérée géographiquement à la valeur AICc de régression linéaire généralisée est une manière d’évaluer les avantages qu’il y a à passer d’un modèle global (régression linéaire généralisé) à un modèle de régression local (régression pondérée géographiquement).
Reportez-vous à la référence Gollini et al. de la section Ressources supplémentaires pour connaître les formules utilisées dans le calcul des valeurs AICc pour tous les types de modèle.
- Sigma-Squared (Sigma carré) : estimation des moindres carrés de la variance (écart type au carré) des valeurs résiduelles. Pour cette statistique, les valeurs réduites sont préférables. Cette valeur est la somme de carrés résiduelle normalisée pour laquelle la somme résiduelle des carrés est divisée par les degrés de liberté effectifs des valeurs résiduelles. Le sigma au carré est utilisé pour le calcul des valeurs AICc.
- Sigma-Squared MLE (Estimation selon le maximum de vraisemblance de Sigma carré) : estimation correspondant à un maximum de vraisemblance de la variance (écart type au carré) des valeurs résiduelles. Pour cette statistique, les valeurs réduites sont préférables. Le calcul de cette valeur consiste à diviser la somme résiduelle des carrés par le nombre d’entités en entrée.
- Degrés de liberté effectifs : cette valeur reflète un compromis entre la variance des valeurs ajustées et la déviation des estimations de coefficient, et est liée au choix de taille du voisinage. Lorsque le voisinage approche de l'infini, les pondérations géographiques pour chaque entité approchent de 1 et les estimations de coefficient sont très proches de celles d'un modèle de régression linéaire généralisée global. Pour les très grands voisinages, le nombre effectif de coefficients se rapproche du nombre réel ; les évaluations de coefficient locales présentent une variance réduite, mais une déviation importante. Inversement, plus la taille du voisinage est réduite et approche de zéro, plus les pondérations géographiques de chaque entité approchent de zéro à l’exception du point de régression. Pour les voisinages extrêmement réduits, le nombre effectif de coefficients correspond au nombre d'observations et les évaluations de coefficient locales présentent une variance importante mais une déviation réduite. Le nombre effectif permet de calculer un grand nombre d’autres mesures diagnostiques.
- Valeur critique ajustée des statistiques pseudo-T : il s’agit de la valeur critique ajustée utilisée pour tester la signification statistique des coefficients dans un test-T bilatéral à une confiance de 95 pour cent. La valeur correspond à un niveau de signification (alpha) de 0,05 divisé par les degrés de liberté effectifs. Cet ajustement contrôle le taux d’erreur par famille (FWER) de la signification des variables explicatives.
Diagrammes en sortie
L’outil génère comme sortie une matrice de nuages de points et un histogramme dans la fenêtre Contenu. La matrice de nuages de points comprend une seule variable dépendante et un maximum de neuf variables explicatives. L’histogramme affiche le résidu d’écart et une courbe de distribution normale.
Binaire (logistique)
Le type de modèle binaire part du principe que les valeurs de la variable dépendante sont binaires (0 ou 1).
Classe d'entités et champs ajoutés
Les entités en sortie qui contiennent les champs relatifs à l’intersection (INTERCEPT), l’erreur standard de l’intersection (SE_INTERCEPT), les coefficients et les erreurs standards pour chaque variable explicative, ainsi que la valeur de la probabilité de valeur 1, la valeur prévue, la valeur résiduelle d’écart, la valeur GInfluence et l’écart de pourcentage local sont également indiqués.
Interpréter des messages et diagnostics
Les détails d’analyse sont fournis dans les messages et incluent le nombre d’entités analysées, les variables dépendantes et explicatives, et le nombre de voisins spécifié. De plus, les diagnostics suivants sont signalés :
- % d’écart expliqué par le modèle global (non spatial) : mesure la qualité de l’ajustement et quantifie la performance d’un modèle global (régression linéaire généralisée). Sa valeur varie de 0,0 à 1,0, les valeurs supérieures étant préférables. Elle peut être interprétée en tant que proportion de variance de la variable dépendante correspondant au modèle de régression.
- % d'écart expliqué par le modèle local : mesure la qualité de l’ajustement et quantifie la performance d’un modèle local (régression pondérée géographiquement). Sa valeur varie de 0,0 à 1,0, les valeurs supérieures étant préférables. Elle peut être interprétée en tant que proportion de variance de la variable dépendante correspondant au modèle de régression local.
- % d'écart expliqué par le modèle local par opposition au modèle global : ce pourcentage permet d’évaluer les avantages du passage d’un modèle global (régression linéaire généralisée) à un modèle de régression local (régression pondérée géographiquement) en comparant la somme des carrés résiduelle du modèle local à la somme des carrés résiduelle du modèle global. Sa valeur varie de 0,0 à 1,0, les valeurs élevées signifiant que le modèle de régression local obtient de meilleurs résultats que le modèle global.
- AICc : mesure des performances du modèle, utile pour comparer des modèles de régression. En considérant la complexité du modèle, un modèle de valeur AICc inférieure fournit un meilleur ajustement aux données observées. La valeur AICc n'est pas une mesure absolue de la qualité d'ajustement mais elle est utile pour la comparaison de modèles avec des variables explicatives différentes, tant qu'ils s'appliquent à la même variable dépendante. Si les valeurs AICc de deux modèles diffèrent de plus de 3, le modèle avec la valeur AICc inférieure est considéré comme meilleur. La comparaison de la valeur AICc de régression pondérée géographiquement à la valeur AICc des moindres carrés ordinaires est une manière d’évaluer les avantages qu’il y a à passer d’un modèle global (moindres carrés ordinaires) à un modèle de régression local (régression pondérée géographiquement).
- Sigma carré : cette valeur est la somme des carrés résiduelle normalisée, où la somme résiduelle des carrés est divisée par les degrés de liberté effectifs de la valeur résiduelle. Il s’agit de l’estimation des moindres carrés de la variance (écart type au carré) des valeurs résiduelles. Pour cette statistique, les valeurs réduites sont préférables. Le sigma au carré est utilisé pour le calcul des valeurs AICc.
- Estimation selon le maximum de vraisemblance de Sigma carré : estimation correspondant à un maximum de vraisemblance de la variance (écart type au carré) des valeurs résiduelles. Pour cette statistique, les valeurs réduites sont préférables. Le calcul de cette valeur consiste à diviser la somme résiduelle des carrés par le nombre d’entités en entrée.
- Degrés de liberté effectifs : cette valeur reflète un compromis entre la variance des valeurs ajustées et la déviation des estimations de coefficient, et est liée au choix de taille du voisinage. Lorsque le voisinage approche de l'infini, les pondérations géographiques pour chaque entité approchent de 1 et les estimations de coefficient sont très proches de celles d'un modèle de régression linéaire généralisée global. Pour les très grands voisinages, le nombre effectif de coefficients se rapproche du nombre réel ; les évaluations de coefficient locales présentent une variance réduite, mais une déviation importante. Inversement, plus la taille du voisinage est réduite et approche de zéro, plus les pondérations géographiques de chaque entité approchent de zéro à l’exception du point de régression. Pour les voisinages extrêmement réduits, le nombre effectif de coefficients correspond au nombre d'observations et les évaluations de coefficient locales présentent une variance importante mais une déviation réduite. Le nombre effectif permet de calculer un grand nombre d’autres mesures diagnostiques.
- Valeur critique ajustée des statistiques pseudo-T : il s’agit de la valeur critique ajustée utilisée pour tester la signification statistique des coefficients dans un test-T bilatéral à une confiance de 95 pour cent. La valeur correspond à un niveau de signification (alpha) de 0,05 divisé par les degrés de liberté effectifs. Cet ajustement contrôle le taux d’erreur par famille de la signification des variables explicatives.
Diagrammes en sortie
Une matrice de nuages de points, ainsi que des boîtes à moustaches et un histogramme des valeurs résiduelles d’écart, sont fournis.
Total (Poisson)
Le type de modèle de Poisson suppose que les valeurs de la variable dépendante sont des totaux.
Classe d'entités et champs ajoutés
Les entités en sortie contiennent les champs relatifs à l’intersection (INTERCEPT), l’erreur standard de l’intersection (SE_INTERCEPT), les coefficients et les erreurs standards pour chaque variable explicative, ainsi que la valeur prévue avant la transformation logarithmique (RAW_PRED), la valeur prévue, la valeur résiduelle d’écart, la valeur GInfluence, l’écart de pourcentage local et l’indice de conditionnement.
Interpréter des messages et diagnostics
Les détails d’analyse sont fournis dans les messages et incluent le nombre d’entités analysées, les variables dépendantes et explicatives, et le nombre de voisins spécifié. De plus, les diagnostics suivants sont signalés :
- % d’écart expliqué par le modèle global (non spatial) : mesure la qualité de l’ajustement et quantifie la performance d’un modèle global (régression linéaire généralisée). Sa valeur varie de 0,0 à 1,0, les valeurs supérieures étant préférables. Elle peut être interprétée en tant que proportion de variance de la variable dépendante correspondant au modèle de régression.
- % d'écart expliqué par le modèle local : mesure la qualité de l’ajustement et quantifie la performance d’un modèle local (régression pondérée géographiquement). Sa valeur varie de 0,0 à 1,0, les valeurs supérieures étant préférables. Elle peut être interprétée en tant que proportion de variance de la variable dépendante correspondant au modèle de régression local.
- % d'écart expliqué par le modèle local par opposition au modèle global : ce pourcentage permet d’évaluer les avantages du passage d’un modèle global (régression linéaire généralisée) à un modèle de régression local (régression pondérée géographiquement) en comparant la somme des carrés résiduelle du modèle local à la somme des carrés résiduelle du modèle global. Sa valeur varie de 0,0 à 1,0, les valeurs élevées signifiant que le modèle de régression local obtient de meilleurs résultats que le modèle global.
- AICc : mesure des performances du modèle, utile pour comparer des modèles de régression. En considérant la complexité du modèle, un modèle de valeur AICc inférieure fournit un meilleur ajustement aux données observées. La valeur AICc n'est pas une mesure absolue de la qualité d'ajustement mais elle est utile pour la comparaison de modèles avec des variables explicatives différentes, tant qu'ils s'appliquent à la même variable dépendante. Si les valeurs AICc de deux modèles diffèrent de plus de 3, le modèle avec la valeur AICc inférieure est considéré comme meilleur. La comparaison des valeurs AICc de la Régression pondérée géographiquement et des Moindres carrés ordinaires est une manière d'évaluer les avantages du passage d'un modèle global (Moindres carrés ordinaires) à un modèle de régression local (Régression pondérée géographiquement).
- Sigma carré : cette valeur est la somme des carrés résiduelle normalisée, où la somme résiduelle des carrés est divisée par les degrés de liberté effectifs de la valeur résiduelle. Il s’agit de l’estimation des moindres carrés de la variance (écart type au carré) des valeurs résiduelles. Pour cette statistique, les valeurs réduites sont préférables. Le sigma au carré est utilisé pour le calcul des valeurs AICc.
- Estimation selon le maximum de vraisemblance de Sigma carré : estimation correspondant à un maximum de vraisemblance de la variance (écart type au carré) des valeurs résiduelles. Pour cette statistique, les valeurs réduites sont préférables. Le calcul de cette valeur consiste à diviser la somme résiduelle des carrés par le nombre d’entités en entrée.
- Degrés de liberté effectifs : cette valeur reflète un compromis entre la variance des valeurs ajustées et la déviation des estimations de coefficient, et est liée au choix de taille du voisinage. Lorsque le voisinage approche de l'infini, les pondérations géographiques pour chaque entité approchent de 1 et les estimations de coefficient sont très proches de celles d'un modèle de régression linéaire généralisée global. Pour les très grands voisinages, le nombre effectif de coefficients se rapproche du nombre réel ; les évaluations de coefficient locales présentent une variance réduite, mais une déviation importante. Inversement, plus la taille du voisinage est réduite et approche de zéro, plus les pondérations géographiques de chaque entité approchent de zéro à l’exception du point de régression. Pour les voisinages extrêmement réduits, le nombre effectif de coefficients correspond au nombre d'observations et les évaluations de coefficient locales présentent une variance importante mais une déviation réduite. Le nombre effectif permet de calculer un grand nombre d’autres mesures diagnostiques.
- Valeur critique ajustée des statistiques pseudo-T : il s’agit de la valeur critique ajustée utilisée pour tester la signification statistique des coefficients dans un test-T bilatéral à une confiance de 95 pour cent. La valeur correspond à un niveau de signification (alpha) de 0,05 divisé par les degrés de liberté effectifs. Cet ajustement contrôle le taux d’erreur par famille de la signification des variables explicatives.
Diagrammes en sortie
Une matrice de nuages de points est fournie dans la fenêtre Contenu (incluant jusqu’à 19 variables) ainsi qu’un histogramme de la valeur résiduelle d’écart et une ligne de distribution normale.
Implémentation : autres conseils et remarques
Dans les modèles de régression globaux, tels que la régression linéaire généralisée, les résultats sont peu fiables si plusieurs variables présentent un phénomène de multicolinéarité (lorsque plusieurs variables sont redondantes ou décrivent la même chose). L’outil Régression pondérée géographiquement génère une équation de régression locale pour chaque entité dans le jeu de données. Lorsque les valeurs d'une variable explicative particulière s'agrègent spatialement, vous risquez de rencontrer des problèmes de multicolinéarité locale. L’indice de conditionnement dans les entités en sortie indique lorsque les résultats sont instables en raison d’un problème de multicolinéarité local. Soyez critique à l’égard des résultats d’entités présentant un indice de conditionnement supérieur à 30, nul ou, pour les shapefiles, égal à -1.7976931348623158e+308. Le numéro de condition est ajusté à l’échelle pour corriger le nombre de variables explicatives dans le modèle. Cela permet de comparer directement le numéro de condition entre les modèles utilisant des nombres de variables explicatives différents.
Les erreurs de conception de modèle indiquent souvent un problème de multicolinéarité globale ou locale. Pour déterminer l’origine du problème, exécutez l’outil Régression linéaire généralisée et examinez la valeur VIF de chaque variable explicative. Si certaines valeurs VIF sont élevées (supérieures à 7,5, par exemple), la multicolinéarité globale empêche la résolution de l’outil. Toutefois, la multicolinéarité locale est plus vraisemblablement à l'origine du problème. Essayez de créer une carte thématique pour chaque variable explicative. Si la carte révèle une agrégation spatiale de valeurs identiques, envisagez la suppression de ces variables du modèle ou la combinaison de ces variables avec d'autres variables explicatives afin d'augmenter la variation des valeurs. Par exemple, si vous modélisez des valeurs d’habitat et que vous disposez de variables pour les chambres et les salles de bains, vous pouvez les combiner pour augmenter la variation des valeurs ou les représenter en tant que superficie de salle de bain/chambre. Évitez d’utiliser un régime spatial artificiel ou des variables binaires pour les modèles de type Gaussien ou Poisson, des variables catégorielles ou nominales spatialement agrégées avec le type de modèle logistique, ou des variables possédant peu de valeurs possibles en créant des modèles de régression pondérée géographiquement.
Les problèmes de multicolinéarité locale peuvent également empêcher l’outil de trouver une bande de distance optimale ou un nombre de voisins optimal. Essayez de définir des intervalles manuels ou une bande de distance définie par l’utilisateur ou un nombre de voisins spécifique. Examinez ensuite les indices de conditionnement dans les entités en sortie pour voir quelles entités sont associées à des problèmes de multicolinéarité locale (indices de conditionnement supérieurs à 30). Vous pouvez supprimer temporairement ces entités en attendant de trouver une distance optimale ou un nombre de voisins optimal. N'oubliez pas que les résultats associés à des conditionnements supérieurs à 30 ne sont pas fiables.
Ressources supplémentaires
Pour en savoir plus sur le fonctionnement de la régression pondérée géographiquement et la régression linéaire généralisée, de nombreuses ressources sont disponibles. Commencez par lire la rubrique Principes de base de l’analyse de régression ou exercez-vous avec le didacticiel Regression Analysis.
Les ressources suivantes sont également utiles :
Brunsdon, C., Fotheringham, A. S., & Charlton, M. E. (1996). "Geographically weighted regression: a method for exploring spatial nonstationarity". Geographical analysis, 28(4), 281-298.
Fotheringham, Stewart A., Chris Brunsdon et Martin Charlton. Geographically Weighted Regression: The analysis of spatially varying relationships. John Wiley & Sons, 2002.
Gollini, I., Lu, B., Charlton, M., Brunsdon, C., & Harris, P. (2015). "GWmodel: An R Package For Exploring Spatial Heterogeneity Using Geographically Weighted Models." Journal of Statistical Software, 63(17), 1–50.https://doi.org/10.18637/jss.v063.i17.
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
Nakaya, T., Fotheringham, A. S., Brunsdon, C., & Charlton, M. (2005). "Geographically weighted Poisson regression for disease association mapping". Statistics in medicine, 24(17), 2695-2717.
Páez, A., Farber, S., & Wheeler, D. (2011). "A simulation-based study of geographically weighted regression as a method for investigating spatially varying relationships". Environment and Planning A, 43(12), 2992-3010.
Vous avez un commentaire à formuler concernant cette rubrique ?