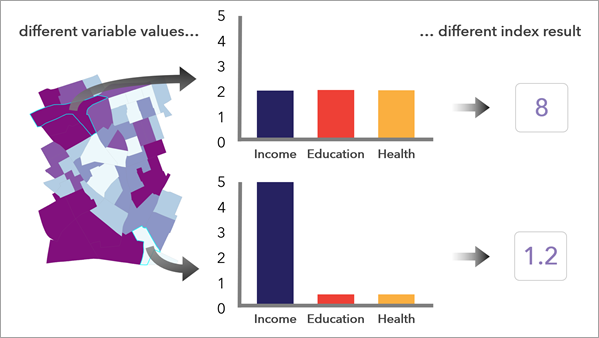
インデックスとは、社会的脆弱性やビジネス イノベーションなど、多くの場合に直接測定または定義することが難しい関心の対象を測定する数値です。 [コンポジット インデックスの計算 (Calculate Composite Index)] ツールは、複数の変数を 1 つの変数に結合することで、インデックスを作成します。 このツールでは、変数を事前処理し、変数を結合し、インデックスを後処理する 3 ステップのワークフローに従います。
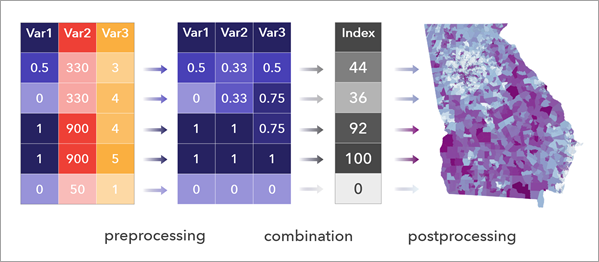
インデックスの適切な構築は、設計時にその目的を熟考することと、伝達時にプロセスを透明化することにかかっています。 [コンポジット インデックスの計算 (Calculate Composite Index)] ツールを使用すると、適切なインデックスの構築プロセスへと導かれ、結果を可視化し理解できるようになります。
ArcGIS でコンポジット インデックスを作成するためのベスト プラクティスの詳細
適用例
[コンポジット インデックスの計算 (Calculate Composite Index)] ツールの適用例を以下に示します。
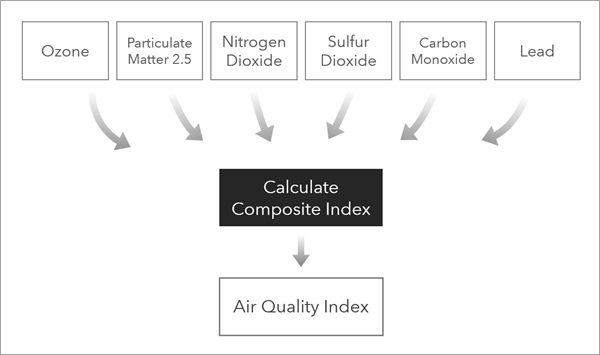
- 環境保護局は、大気汚染に関する公共政策を一般の人に伝達するために、大気質インデックスを作成したいと考えています。 基準汚染物質に対応するデータは監視局から収集しています。 アナリストは [コンポジット インデックスの計算 (Calculate Composite Index)] ツールを実行して、個々の汚染物質インジケーターを 1 つの大気質インデックスに結合することができます。
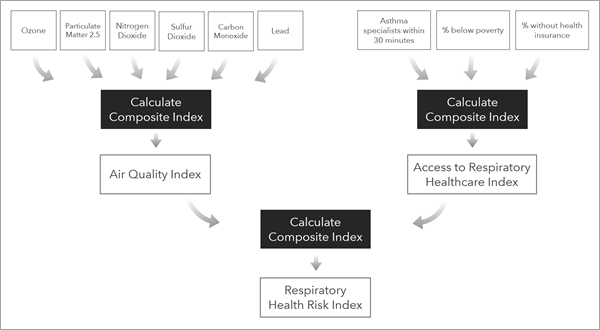
- 公衆衛生局は、呼吸器健康リスク インデックスを作成して、環境面の不公正をハイライトしたいと考えています。 このために、アナリストは [コンポジット インデックスの計算 (Calculate Composite Index)] ツールを複数回実行して、複数のサブインデックスによる 1 つのインデックスを作成できます。ここでは、ツールの最初の実行時にさなざまなドメインのサブインデックスが作成され、ツールの最終実行時に最終的なインデックスが作成されます。
- 所管ではインフラ整備の補助金申請を行いたいと考えており、資格を得るために、十分なサービスを受けていないコミュニティにリソースが行き渡るようになることを証明する必要があります。 彼らはインフラストラクチャと人口統計の変数を組み合わせたインデックスを作成し、最もサービスを必要としている地域を特定することができます。
変数の事前処理の方法
適切なインデックスを作成するには、変数を互換性のあるスケールにする必要があります。 このために、このツールには事前処理のオプションが提供されています。異なる入力変数を共通の測定スケールに合わせることで、適切に結合できるようになります。 このツールではオプションで変数を反転させることもできます。これにより、各変数の高い値の意味がお互いに一致するようになります。
注意:
[フィールドの変換 (Transform Field)] ツールを使用して、変数を変換します。
変数の向きを反転するための事前処理
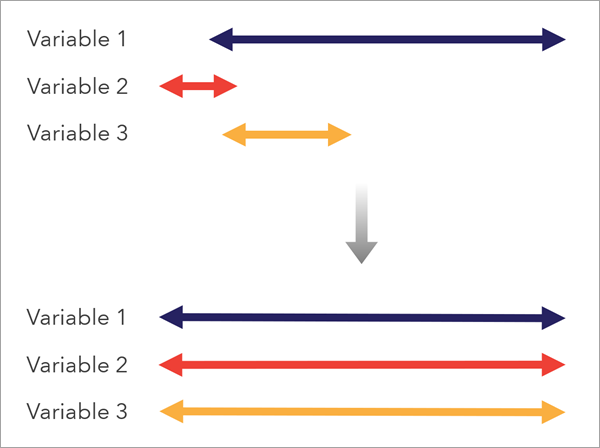
各変数の低い値と高い値の意味を検討し、これらが相互に一貫性を持つようにします。 たとえば、社会的脆弱性のインデックスでは、世帯所得平均の低い場所の方が脆弱ですが、保険に加入していない人の割合が低い場所の方が脆弱性は低くなります。これらの脆弱性の向きは、インデックスの目的のコンテキストにおいて反対を向いているのです。
各変数をツールに入力するときに、変数を反転させる必要があるかどうかを検討します。この場合は、[方向の反転] チェックボックスをオンにして、変数の向きを反転させます。
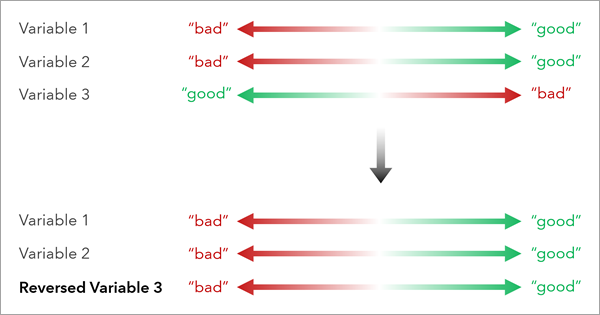
変数の反転は、各値に -1 を乗算し、変数の元の範囲でフィールドをスケール処理することで計算します。
同じスケールを使用するための変数の事前処理
[入力変数をスケール処理する方法] パラメーターを使用して、共通のスケール処理方法を選択します。 選択した方法はすべての変数の適用され、結果のフィールドが出力で提示されます。 次のオプションを利用できます。
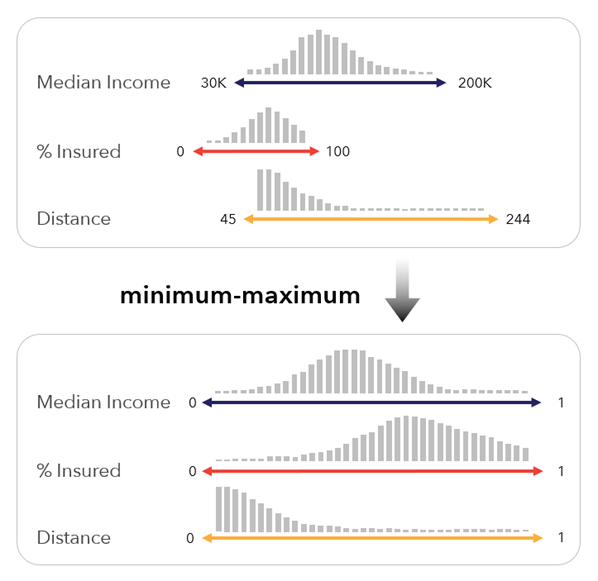
[最小値-最大値] - 各変数の最小値と最大値を使用して、変数が 0 ~ 1 でスケール処理されます。 入力変数の分布が保持され、わかりやすい 0 ~ 1 のスケールでスケール処理されるため、この方法は最も簡単です。
この方法には次の式が適用されます。
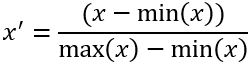
この方法では変数の分布が保持されるので、傾斜分布や外れ値による影響を受ける可能性があります。 たとえば、非常に高い値の外れ値が 1 つ存在する場合、この外れ値は値 1 を受け取りますが、残りの値は似たようなものになり、ゼロに近づきます。 変数を事前処理してばらつきを減らすことで、この変数が結果のインデックスに与える影響を少なくすることができます。
この方法は、入力データの最小値と最大値にも依存します。このため、変数の最小値と最大値が各時間ステップで変化するような場合、複数の時間間隔でのインデックスの比較には適さなくなります。
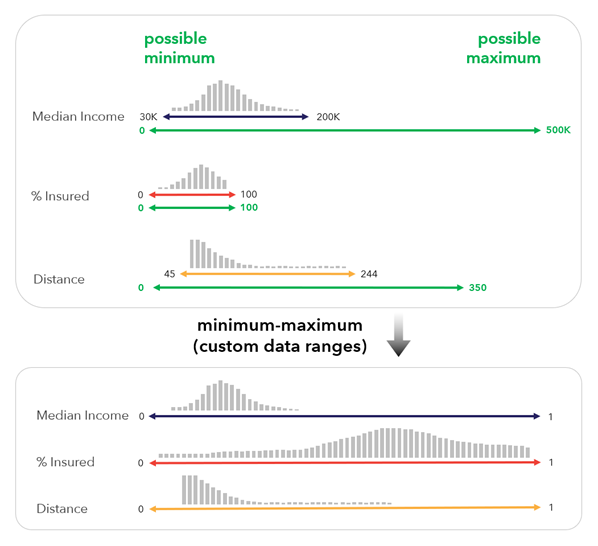
[最小値-最大値 (カスタム データ範囲)] - 各変数に設定可能な最小値と最大値を使用して、変数が 0 ~ 1 でスケール処理されます。 この方法は、設定可能な最小値と最大値が変数の範囲内に存在しない場合や、追加データの収集時に比較可能なままでなければならないインデックスを作成する場合に役立ちます。
この方法には次の式が適用されます。
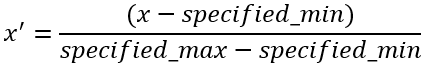
設定可能な最小値と最大値の設定には、複数の用途があります。
- 時間をまたいでインデックスを比較するときに、そのインデックスが別の期間にあったかもしれない値の範囲を現在のデータが表していない場合。
- 参照統計情報 (非常に広い分析範囲の最小値と最大値など) が存在する場合。 たとえば、分析範囲がフランスに設定されたインデックスは、ヨーロッパのすべての国を基準とする最小値と最大値を使用する可能性があります。
- 人の発達インデックスにおける野心的な平均余命など、野心的なベンチマークが存在する場合。 データそのものには野心的な平均余命が含まれない可能性がありますが、それでもベンチマークはインデックスのコンテキスト設定に使用されます。
- 変数の理論上の最小値と最大値のアプリオリな知識がある場合。たとえば、地球上の絶対温度の範囲を知っていて、もっと小さい範囲の日々の記録を使用する場合など。
[パーセンタイル] - 変数を 0 ~ 1 のパーセンタイルに変換します。 この方法は、各変数のランクが実際の値よりも重要な場合に役立つ可能性があります。 変数が一様分布に変換されるので、外れ値や傾斜分布があっても安定しています。
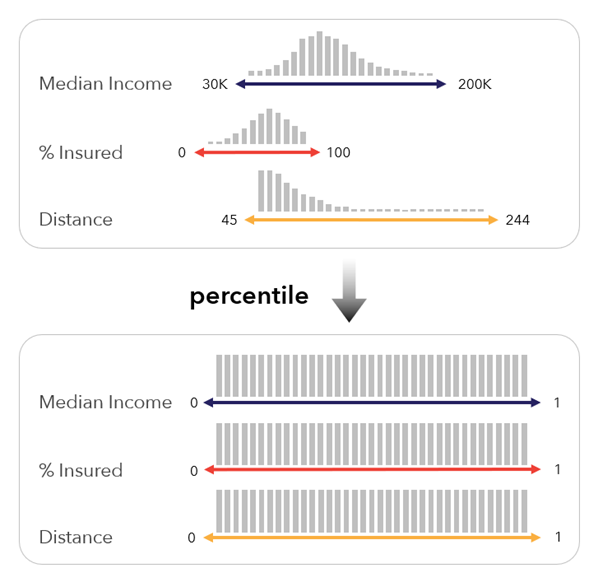
パーセンタイルにはさまざまな定義があります。 この方法には次の式を使用します。
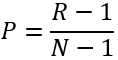 、
、ここで R は順序ランク (タイの場合は最小ランク値を使用)、N は値の数、P は結果のパーセンタイルです。
パーセンタイルは、変数内の他の値を基準にして値の位置を示します。 たとえば、5 万ドルと 6 万ドルの収入差は大きくないかもしれませんが、その間の値を持つ多くのフィーチャがあれば、パーセンタイルの差は大きくなると考えられます。
[ランク] - 入力値をランク付けします。変数の中の最低値に 1 の値を割り当て、値ごとに 1 ずつ増分させていきます。 この方法は、各変数のランクが実際の値よりも重要な場合に役立つ可能性があります。 この方法も、外れ値や傾斜分布に対して安定しています。
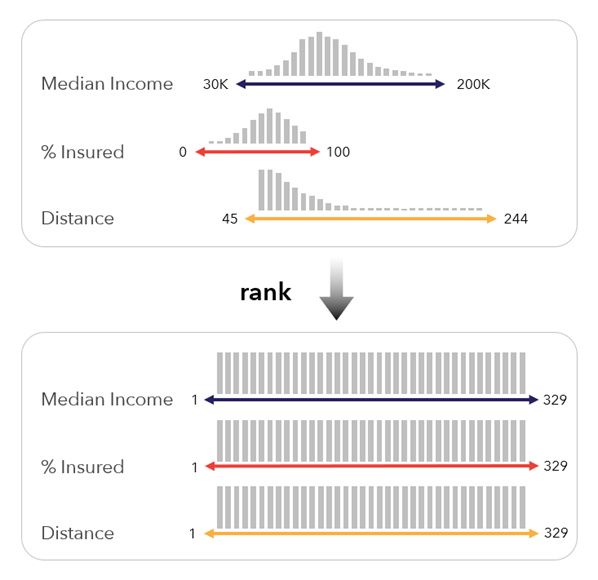
この方法はランク平均方法を使用します。タイが観測されたら平均ランク値を割り当てることで、タイを解決します。
この方法はパーセンタイルとよく似ていますが、値の範囲が 1 からテーブル内のレコード数までです。
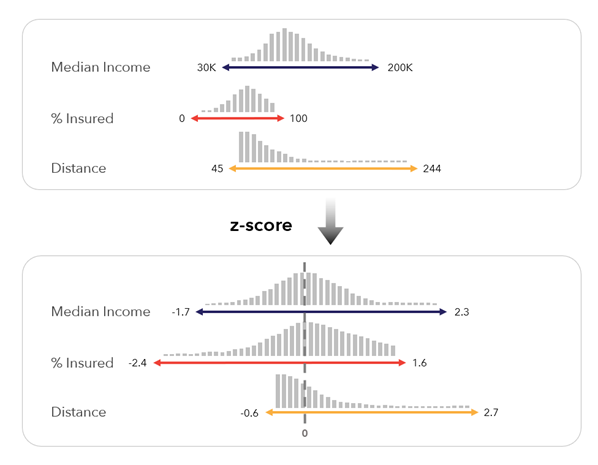
[Z スコア] - Z スコアの式を使用して各変数を標準化します。 この方法は、各値を変数の平均に対して考慮する必要がある場合に役立ちます。 たとえば、貧困線を下回る人の割合が全国平均より高いのか、低いのか、平均との差はどの程度なのかを知りたい場合です。
この方法には次の式を使用します。
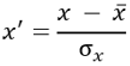 、
、ここで x' は Z スコア、x は元の値、x̄ は平均値、σ は標準偏差です。
Z スコアは標準偏差数 (データ内の分散の測定) で表します。 Z スコアが 2 の場合はフィーチャが平均を上回る 2 つの標準偏差だという意味で、Z スコアが -1 の場合は平均を下回る 1 つの標準偏差だという意味です。 この方法は、最小値-最大値の方法と比べると、外れ値による影響を受けにくいと考えられます。 ただし、負の値が生成されるので、乗法結合法との互換性がなくなります。
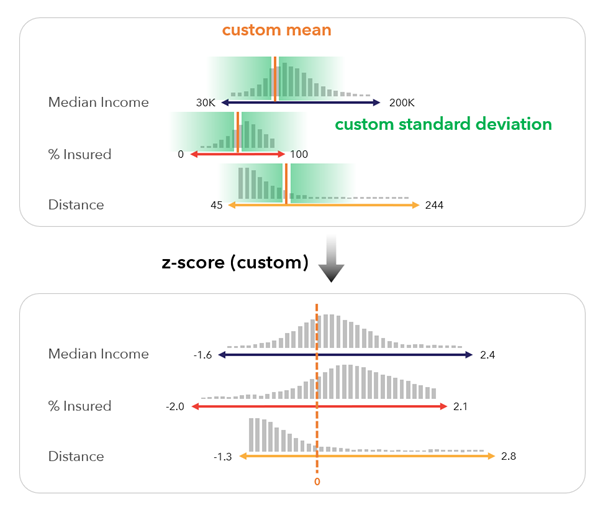
[Z スコア (カスタム)] - カスタム平均とカスタム標準偏差で Z スコアの式を使用して各変数を標準化します。 この方法は、参照統計情報との比較または時間をまたぐ比較を行うインデックスを作成する場合に役立ちます。
この方法には次の式を使用します。
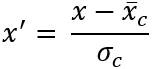 、
、ここで x' は標準化後の値、x は元の値、x̄c はカスタム平均値、σc はカスタム標準偏差です。
[カスタム標準化] パラメーターを使用して、参照の平均と標準偏差を設定します。
たとえば、最初の年を比較ポイントとして使用して次の 10 年間の更新を行う年次発達インデックスを作成するには、変数ごとの実際の平均と標準偏差を使用する Z スコア オプションを使用して、最初の年のインデックスを作成します。 さらに、その後の年の [カスタム標準化] パラメーターで、同じ平均と標準偏差を使用します。 これにより、最初の年の分布を比較対象として、すべての年の結果が比較可能になります。
この方法は、データ上の平均と同じでないことがある理論上の平均との比較にも役立ちます。 たとえば、国全体の失業率は 8 パーセントなのに、データ上の平均失業率が 13 パーセントである場合、Z スコアは国全体の平均や標準偏差に関して設定することができます。データ内のサンプルは、全国平均よりも高い失業率を反映してもっとプラスの値になります。
[閾値によるフラグ (バイナリ)] - 指定された閾値よりも値が上なのか下なのかを示すバイナリ値 (0、1) に変数を変換します。 この方法は、特定の値をハイライトすることが重要で、値のばらつきは重要でない場合に役立ちます。
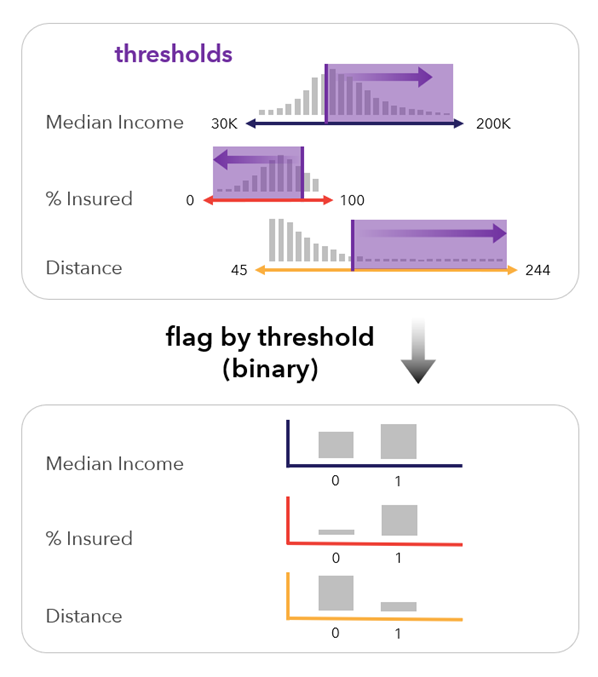
このオプションにより [閾値に合わせてスケール処理する方法] パラメーターがアクティブになります。これにより、スケール処理された変数の範囲に閾値を設定できるようになります。
この方法にはさまざまな用途があります。
- 大気質ドメインの専門家は、複数の大気質変数について、人の健康上の閾値を超えている場所をハイライトしたいと考えています。 この場合は [閾値に合わせてスケール処理する方法] パラメーターの変数を RAW に設定し、閾値を設定します。
- 政府機関では、複数のドメインで非常に脆弱性が高い場所をハイライトしたいと考えています。 この場合は [閾値に合わせてスケール処理する方法] パラメーターをパーセンタイルに設定し、各変数の閾値を 0.9 [より大きい] に設定して、最も恵まれない場所をハイライトします。
- 国際組織では、人の発達インジケーターで一貫して平均を下回っている国々をハイライトしたいと考えています。 この場合は [閾値に合わせてスケール処理する方法] パラメーターを Z スコアに設定し、閾値を 0 [より小さい] に設定して、平均を下回る場所をハイライトします。
この方法は、合計結合オプションと組み合わせて、1 つの場所が閾値を超える回数をカウントする場合に非常に役立ちます。
この方法は入力変数の外れ値の影響は受けませんが、各変数がバイナリ (0、1) 形式に変換されるので、各入力変数の間隔レベルの情報が失われます。
[ロウの値] - 変数の元の値を使用します。
この方法は、すべての変数が比較可能なスケールである場合のみ使用されます。 たとえば、すべての変数が、パーセンテージや百万分率などの標準単位である場合です。 この方法は、ツールの実行前に、変数の標準化や変換がすでに行われている場合にも有効です。
注意:
選択したスケーリング オプションがすべての変数に適用されます。 各変数に別々のスケーリング オプションを適用する必要がある場合は、このツールを使用する前に、[フィールドの標準化 (Standardize Field)] や [フィールドの再分類 (Reclassify Field)] といった他のツールを使用してください。
フィールドに Null が含まれている場合、このツールではレコードのインデックスを計算することができません。 必要に応じて、[欠損値の補完 (Fill Missing Values)] ツールを使用して値を転嫁することを考えるか、そうでない場合は補完データを見つけてください。
ツールで変数を結合して 1 つのインデックスを作成する方法
変数を事前処理して共通のスケールにすると、変数が集約されて 1 つの値が生まれます。 [スケール処理済みの変数を結合する方法] パラメーターには次のオプションがあります。
- 合計
- 平均
- 乗算
- 幾何補正平均値
[合計] および [平均] オプションは加法、[乗算] および [幾何補正平均値] オプションは乗法であると見なされます。
加法
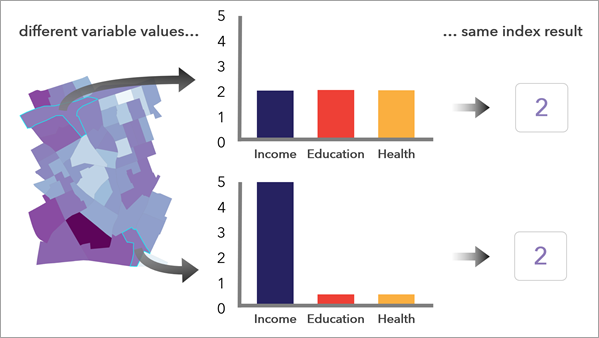
[合計] および [平均] の組み合わせ法は比較的わかりやすく、さまざまなインデックスでよく使用されます。 これらの方法はほぼ同じです。スケールのみが異なる同じ形状の分布が出来上がるので、結果のインデックス マップも同じ表示になります。 値が違うだけです。
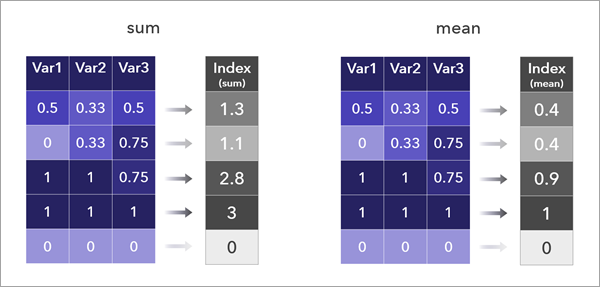
これらの方法では、1 つの変数の高い値が別の変数の低い値を補正することが許されます。
乗法
[乗算] および [幾何補正平均値] 方法の使用にはもっと注意を要します。結果のインデックス値が加法の使用時よりもはるかに高い値になる可能性があり、負の値を使用するとうまく機能しない方法だからです。
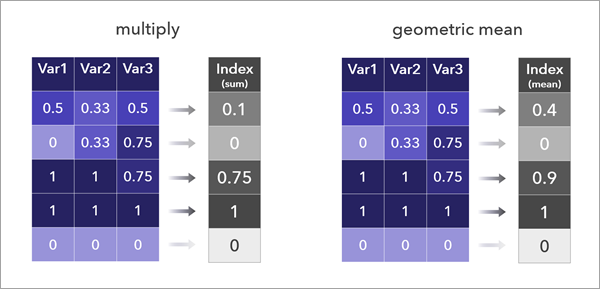
こうした短所もありますが、乗法には、1 つの変数の高い値が別の変数の低い値を補正できないという長所があります。1 つのインデックス値を高くすると、複数の変数が必ず高い値になります。
注意:
[変数のスケール処理方法と結合方法の事前設定] パラメーターは、インデックスの作成でよく使用されているアプローチに基づいて事前設定と結合方法を設定するテンプレートを提供しています。
ウェイト
変数を重み付けして、各因子がインデックスに寄与するときの相対的な重要度を表すことができます。 デフォルトで、すべてのウェイトは 1 に設定され、各変数が同等に重み付けされることを意味します。 ただし、他の変数との比較による変数の相対的な寄与度の差異を示すことが重要な場合があります。 いずれかの変数のウェイトを 2 に変更し、他の変数のウェイトを 1 のままにすると、最終的なインデックスへの寄与において、その変数が他の変数の 2 倍の重要度を持つと見なされることを表示できます。
合計で 1 になるウェイトを使用することもできます。たとえば、3 つの変数が使用されており、そのうちの 1 つの変数がそれ以外の 2 つの変数よりも 2 倍重要であると思われる場合は、ウェイトの値として 0.5、0.25、0.25 を使用できます。
加法では、各変数とそれぞれのウェイトを掛け合わせることで、ウェイトが適用されます。 乗法では、各変数をそれぞれのウェイトで累乗することで、ウェイトが適用されます。
ウェイトは、結果として生成されるインデックスに大きく影響します。 同じウェイトを維持しようと、ウェイトを必要な変数に変更しようと、ウェイトを使用すれば分析に主観性が加わります。 また、変数間の分散の相関や差異によって、ユーザーが無意識に重み付けを行うこともあります。 インデックスの相関や分散の影響の詳細については、コンポジット インデックス作成のためのベスト プラクティスに関するドキュメントをご参照ください。
インデックスの事後処理の方法
変数を事前処理して RAW インデックスに結合した後、事後処理を行うことでインデックスをさらに理解しやすいものにできます。 [出力設定] パラメーター カテゴリのオプションを使用して、方向の調整、スケールの調整、値の分類を行うことができます。
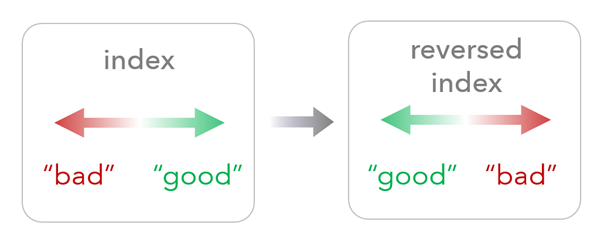
インデックスの反転
インデックスの目的を考えて、大きいインデックス値が目的に合ったものなのか評価します。 [出力インデックス値の反転] パラメーターのチェックボックスを使用して、オプションで RAW インデックスを反転させ、大きいインデックス値が小さい値を表すように (またはその逆に) することができます。
注意:
乗法でのインデックス値の反転を行うには注意を要します。これらの結果は入力変数の反転と異なるからです。
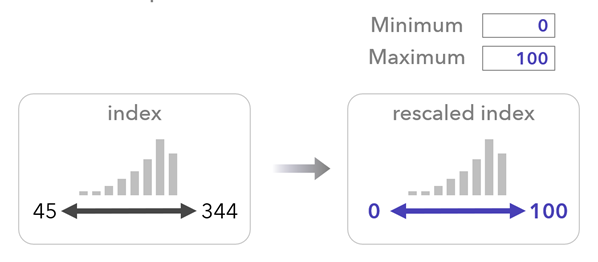
最小値と最大値を使用したインデックスのスケール処理
[出力インデックスの最小値と最大値] パラメーターを使用して、出力インデックスの範囲を指定します。 このオプションは、選択された事前設定や結合方法に関係なく、スケールがわかりやすくするように役立てることができます。 たとえば、RAW インデックスをこの範囲にスケール処理するには、[最小値] に 0、[最大値] に 100 を指定します。 このオプションでは次の式を使用します。
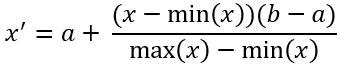 、
、
ここで x は元の値、min(x) はインデックスにある最小値、max(x) はインデックスにある最大値、a は指定された最小値、b は指定された最大値、x' はスケール処理された値です。
インデックスの分類
RAW インデックスの出力に加えて、オプションで出力インデックスを分類し、結果の確認に役立てることができます。 [追加分類出力] パラメーターでは、[等間隔]、[等量分類]、[標準偏差]、[カスタム] という 4 つの方法を使用できます。それぞれで出力に追加フィールドが作成されます。
等間隔方法では、インデックス範囲が同じ長さの間隔に区切られます。
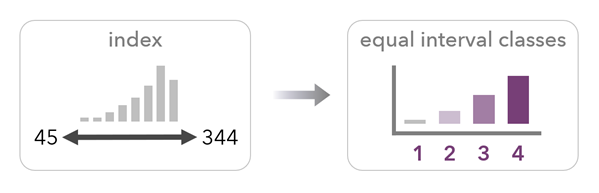
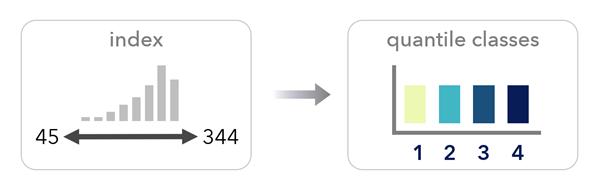
等量方法では、値がクラスに分けられ、各クラスに同じ数のフィーチャまたは行が含まれます。 この方法ではインデックス パーセンタイル レイヤーと似たマップが作成されますが、連続パーセンタイル分布とは異なり、クラスが使用されます。 このオプションを使用して、クラス数に基づき、五分位 (5 クラス)、十分位 (10 クラス)、またはその他のタイプの等量分類のマップを作成します。
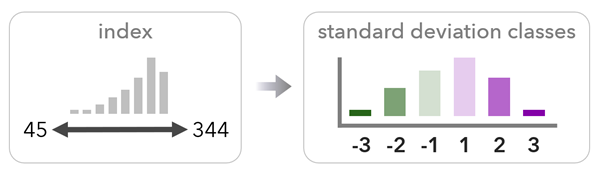
標準偏差方法では、インデックスを分類して、各値の平均からの位置である標準偏差の数値を示します。
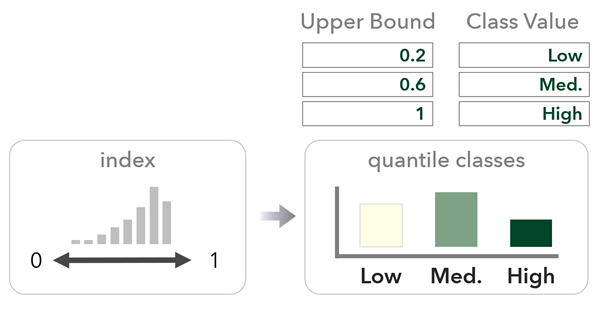
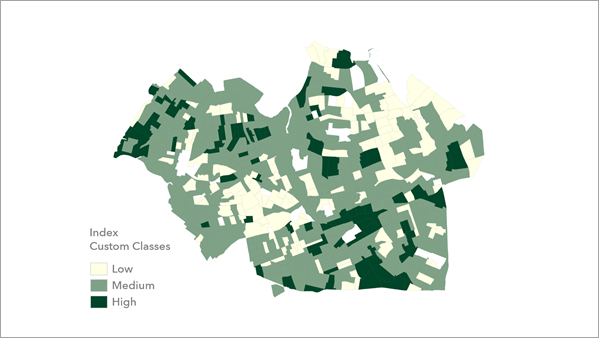
カスタム クラス方法では、カスタム クラス範囲とカスタム ラベルを使用して、連続インデックスを分類します。 数値ラベルまたはテキスト ラベル ([低]、[中]、[高] など) を追加できます。
結果の解析
結果のインデックスを可視化して調査することは、インデックスを将来的に使用できるようにする上で重要なステップです。 このツールでは、結果の解釈に役立つように、さまざまなマップやチャートが作成されます。
出力レイヤー
(入力に追加するのではなく) [出力フィーチャまたはテーブル] パラメーターをフィーチャクラスまたはシェープファイルに設定すると、出力グループ レイヤーに含まれる複数のレイヤーが作成されます。
ヒント:
Ctrl キーと Shift キーのショートカットを使用して、グループ レイヤー内のレイヤーをすばやく表示したり折りたたんだりできます。
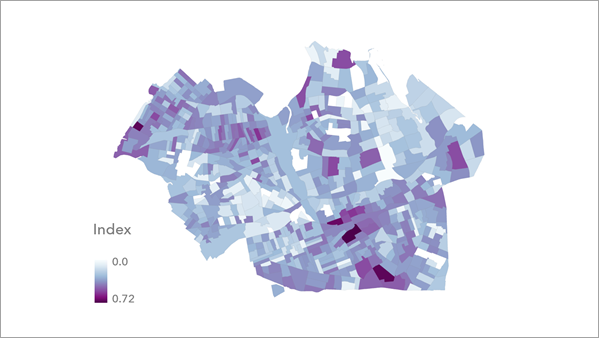
インデックス レイヤー オプションでスケール処理や反転を行った後のインデックス値の分布を表します。 レイヤーには連続のコロプレス マップがあり、これを使用してインデックスの結果を評価できます。 このマップを使用して、インデックス分布や外れ値を維持したまま、大きいインデックス値と小さいインデックス値を評価できます。
インデックス パーセンタイル レイヤーには、インデックス値の間の相対位置 (ランク) が表示されます。 作成されるマップの色はインデックス値のランクに対応しているため、分布状態や実際のインデックスの差異感は維持されません。 この方法は、インデックス ランクに基づいて場所同士がどのように関連するのか評価する場合に使用します。

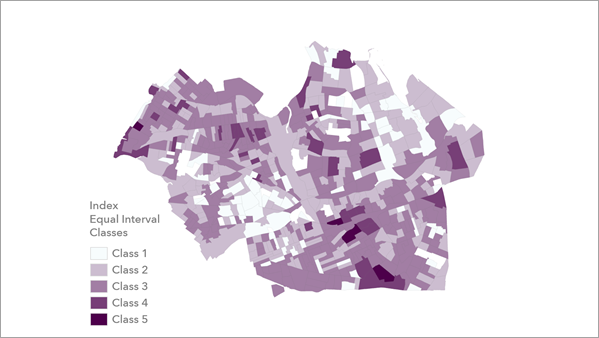
インデックス等間隔クラス レイヤーには、値のインデックス分布に基づいてクラスが表示されますが、[クラスの出力インデックス番号] パラメーターで設定した等間隔に基づいて、値がクラスにグループ化されています。 このレイヤーはインデックス レイヤーの 1 つの分類形式です。
インデックス等量レイヤーは、各クラスに同じ数のフィーチャを割り当てるもので、インデックス パーセンタイル レイヤーの 1 つの分類形式です。 クラスの数は [クラスの出力インデックス番号] パラメーターで設定します。

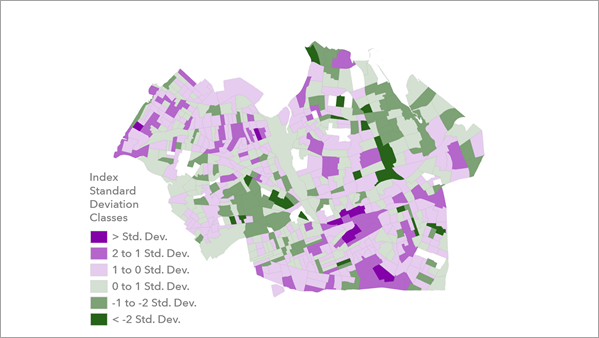
インデックス標準偏差クラス レイヤーには、インデックスの平均値を上回る場所と下回る場所が表示されます。 極端に大きいまたは極端に小さいインデックス値は配色で強調することができ、さらに調査が必要だと思われる場所の特定に役立ちます。
インデックス カスタム クラス レイヤーには、マップ上で指定されたカテゴリが表示されます。このレイヤーは、計画介入に基づいて連続するインデックスを不均一なカテゴリに分割する場合など、多くの目的に使用できます。 たとえば、クラスには [低]、[中]、[高] という名前を付けることができます。
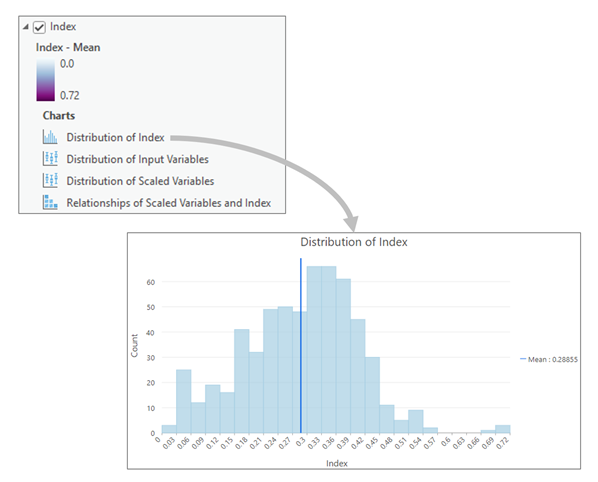
出力チャート
このツールでは、インデックスに関するさまざまな質問に答えるために役立つチャートが作成されます。
インデックスの分布の調査
グループ レイヤー出力の主インデックス レイヤーには、インデックス分布のヒストグラムが含まれます。 これをマップと組み合わせることで、結果の分布についての理解を深めるために役立ちます。
入力変数の分布の調査
主インデックス レイヤーには、入力変数の 2 つの箱ひげ図が含まれています。1 つはスケール処理前の変数分布を表示し、もう 1 つはスケール処理後の変数分布を表示しています。 この 2 つのチャートを並べて比較することで、選択したスケール処理方法による入力変数の変更状況の評価に役立つことがよくあります。 これらのチャートを並べて比較すると、選択したスケール処理方法が変数の分布に、意図された効果をもたらしたかどうかを評価することができます。
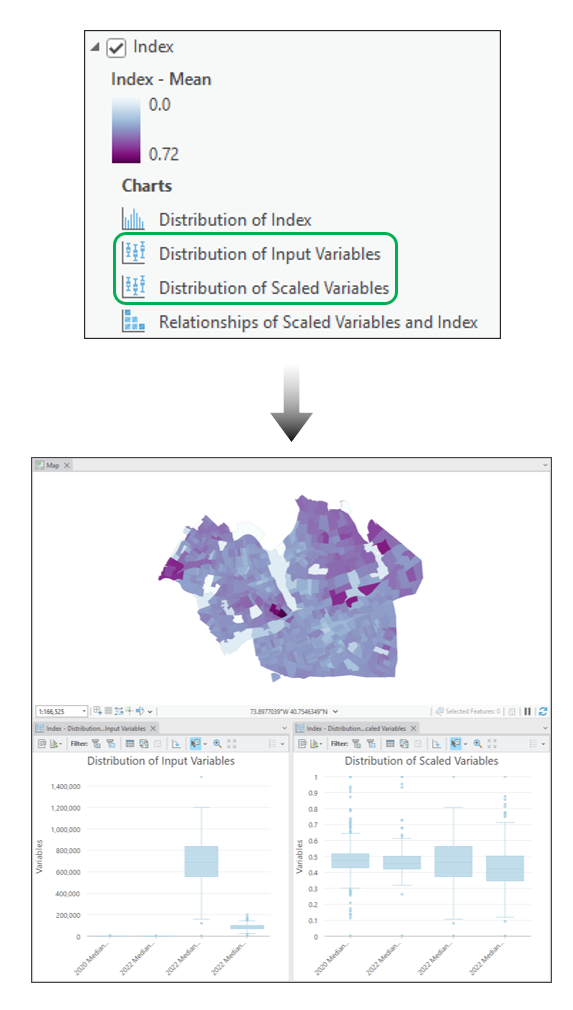
この箱ひげ図を使用して外れ値を調査することもできます。このためには、入力変数の箱ひげ図で外れ値を選択し、マップ上でその場所を確認します。 次に、事前処理された変数の箱ひげ図を表示して、選択した事前処理方法によって外れ値の影響が修復されたかどうか確認できます。
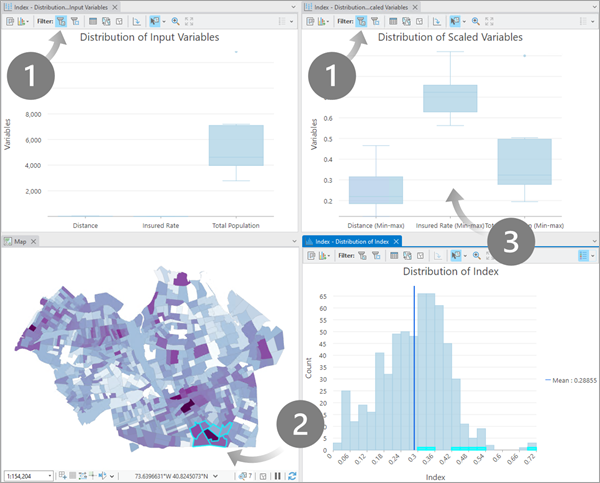
各フィーチャの結果についての調査
マップ、ヒストグラム、2 つの箱ひげ図を開き、2 つの箱ひげ図の選択フィルターを有効にすることで、マップまたはヒストグラム上のフィーチャを選択し、選択内容の入力変数値の分布を可視化することができます。 また、マップと箱ひげ図上の範囲フィルターを使用して、マップ上のさまざまな地域の変数分布を評価することもできます。
インデックスに影響する変数の調査
インデックス レイヤーには、インデックスと使用される各変数の間の相関関係を表示する散布図マトリックスが含まれています。 インデックスに対して高い相関関係を持つ変数は、一般にはインデックスに最も大きく寄与する変数に対応しています。 このため、インデックスとの相関関係が低い変数は、インデックスに与える影響が小さいと見なされることになります。 さらに、内部変動が小さい変数があるかどうかを考慮します。変動の少ない変数はインデックスに有意な情報を提供する可能性が低いからです。
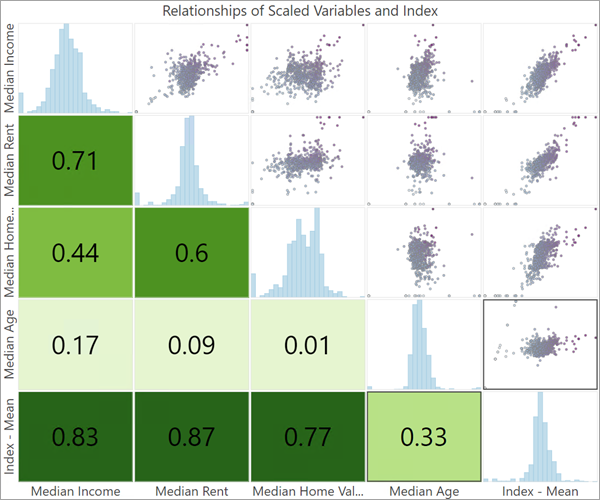
視覚化されたマップとデータによって、インデックスの調整や改良がさらに促されます。 インデックスの作成と評価を行う場合のその他の注意事項の詳細については、ベスト プラクティスのテクニカル ペーパーをご参照ください。
参考資料
Organisation for Economic Co-operation and Development Handbook on Constructing Composite Indicators: Methodology and User Guide をご参照ください。