


Análisis de vínculos es una técnica de análisis que se centra en las relaciones y conexiones en un dataset. Análisis de vínculos le proporciona la capacidad de calcular medidas de centralidad (es decir, grado, intermediación, cercanía y vector propio) y ver las conexiones en un gráfico de vínculos o un mapa de vínculos.
Acerca del análisis de vínculos
Análisis de vínculos utiliza una red de vínculos y nodos interconectados para identificar y analizar relaciones que no se aprecian fácilmente en los datos sin procesar. Entre los tipos habituales de redes se encuentran los siguientes:
- Redes sociales que muestran quién se dirige a quién
- Redes semánticas que ilustran temas relacionados entre sí
- Redes de conflicto que indican alianzas de conexiones entre jugadores
- Redes de tráfico aéreo que indican qué aeropuertos tienen vuelos de conexión
Ejemplos
Un analista delictivo está investigando una red delictiva. Los datos de registros telefónicos pueden utilizarse para determinar la relación y la jerarquía entre los miembros de la red.
Una compañía de tarjetas de crédito está desarrollando un nuevo sistema para detectar el robo de tarjetas de crédito. El sistema utiliza los patrones conocidos de transacción de cada cliente, por ejemplo, ciudad, tiendas y tipos de transacciones, para identificar anomalías y alertar al cliente de un posible robo.
Un analista de salud pública está investigando la crisis de opiáceos en Norteamérica. El analista utiliza datos demográficos y de recetas para identificar nuevos patrones que están emergiendo a medida que la crisis se propaga.
Cómo funciona el análisis de vínculos
La tabla siguiente proporciona una descripción general de la terminología del análisis de vínculos:
| Plazo | Descripción | Ejemplos |
|---|---|---|
Red | Un conjunto de nodos y vínculos interconectados. | Una red social en línea, que utiliza una red de perfiles y relaciones para conectar usuarios. Redes de tráfico aéreo, que utilizan una red de aeropuertos y vuelos para transportar a viajeros de su origen a su destino. |
Nodo | Un punto o vértice que representa a un objeto, por ejemplo, persona, lugar, tipo de delito o tuit. El nodo también puede incluir propiedades asociadas. | Los perfiles de una red social. Las propiedades asociadas pueden incluir el nombre de usuario, la población de origen o el empleador. Los aeropuertos de una red de tráfico aéreo. Las propiedades asociadas pueden incluir el nombre del aeropuerto. |
Vínculo | Las relaciones o conexiones entre nodos. El vínculo también puede incluir propiedades asociadas. | La relación entre perfiles de una red, por ejemplo, amigo, seguidor o conexión. Las propiedades asociadas pueden incluir la duración de la relación. Los vuelos entre aeropuertos de una red de tráfico aéreo. Las propiedades asociadas pueden incluir el número de vuelos entre aeropuertos. |
Centralidad
La centralidad es una medida de importancia para los nodos de una red.
La centralidad en general se utiliza con los siguientes fines:
- Evaluar la influencia de un nodo sobre otros nodos de una red. Por ejemplo, ¿qué usuario ampliará más su audiencia cuando comparta una noticia u oferta de trabajo?
- Identificar los nodos que están más influenciados por otros nodos. Por ejemplo, ¿qué aeropuerto se verá más afectado por vuelos cancelados debido a una tormenta en una otra región?
- Observar el flujo o la propagación de algo por la red, incluida información, objetos o fenómenos. Por ejemplo, ¿cómo se mueve un paquete del almacén hasta la dirección de entrega?
- Comprender qué nodos propagan fenómenos por la red de forma más eficiente. Por ejemplo, ¿qué periódico o canal debería estar conectado para que la historia llegue a más gente?
- Localizar nodos que pueden bloquear o prevenir la propagación de fenómenos. Por ejemplo, ¿dónde deberían estar ubicadas las clínicas de vacunación para detener la propagación de un virus?
Existen cuatro formas de medir la centralidad en Insights: centralidad de grado, centralidad de intermediación, centralidad de cercanía y centralidad del vector propio.
Los cálculos para las centralidades de intermediación, cercanía y vector propio se pueden ponderar o no ponderar.
Centralidad de grado
Centralidad de grado se basa en el número de conexiones directas que un nodo tiene. Centralidad de grado se debería usar cuando se desea determinar qué nodos tienen la influencia más directa. Por ejemplo, en una red social, los usuarios con más conexiones tendrían una centralidad de grado más elevada.
La centralidad de grado del nodo x se calcula utilizando la siguiente ecuación:
degCentrality(x)=deg(x)/(NodesTotal-1)donde:
- NodesTotal = número de nodos de una red
- deg(x) = número de nodos conectados al nodo x
Si los vínculos están direccionados, es decir, si la información fluye entre los nodos en una única dirección, la centralidad de grado puede medirse como grado de entrada o grado de salida. En el caso de una red social, el grado de entrada se basaría en el número de perfiles que el usuario sigue, mientras que el grado de salida se basaría en el número de seguidores que tiene el usuario.
La centralidad de grado de entrada se calcula utilizando la siguiente ecuación:
indegCentrality(x)=indeg(x)/(NodesTotal-1)donde:
- NodesTotal = número de nodos de una red
- indeg(x) = número de nodos conectados al nodo x con el flujo dirigido hacia el nodo x
La centralidad de grado de salida se calcula utilizando la siguiente ecuación:
outdegCentrality(x)=outdeg(x)/(NodesTotal-1)donde:
- NodesTotal = número de nodos de una red
- outdeg(x) = número de nodos conectados al nodo x con el flujo dirigido en dirección contraria al nodo x
Para gráficos direccionados, Insights mide nodos por centralidad de grado de salida de forma predeterminada.
Centralidad de intermediación
Centralidad de intermediación se basa en la medida en que un nodo forma parte de la ruta más corta entre otros nodos. Centralidad de intermediación se debería usar cuando se desea determinar qué nodos se utilizan para conectar otros nodos entre sí. Por ejemplo, un usuario de una red social con conexiones a varios grupos de amigos tendrá una centralidad de intermediación mayor que usuarios con conexiones a un solo grupo.
La centralidad de intermediación del nodo x se calcula utilizando la siguiente ecuación:
btwCentrality(x)=Σa,bϵNodes(pathsa,b(x)/pathsa,b)donde:
- Nodes = todos los nodos de la red
- pathsa,b = el número de rutas más cortas entre todos los nodos a y b
- pathsa,b(x) = el número de rutas más cortas entre los nodos a y b que están conectados a través del nodo x
La ecuación anterior de centralidad de intermediación no tiene en cuenta el tamaño de la red, por tanto, las redes grandes tenderán a tener valores de centralidad de intermediación mayores que las redes pequeñas. Para permitir comparaciones entre redes de diferentes tamaños, la ecuación de centralidad de intermediación se debe normalizar dividiendo entre el número de pares de nodos en el gráfico.
La siguiente ecuación se utiliza para normalizar un gráfico no direccionado:
1/2(NodesTotal-1)(NodesTotal-2)donde:
- NodesTotal = número de nodos de una red
La siguiente ecuación se utiliza para normalizar un gráfico direccionado:
(NodesTotal-1)(NodesTotal-2)donde:
- NodesTotal = número de nodos de una red
Centralidad de cercanía
Centralidad de cercanía se basa en la media de la distancia de ruta de red entre nodos más corta. Centralidad de cercanía se debería usar cuando se desea determinar qué nodos están más asociados a los otros nodos de la red. Por ejemplo, un usuario con más conexiones en una red social tendrá una centralidad de cercanía mayor que un usuario que esté conectado a través de otras personas (en otras palabras, un amigo de un amigo).
Nota:
La distancia entre nodos hace referencia al número de vínculos que los separa, no a la distancia geográfica.
La centralidad de cercanía del nodo x se calcula utilizando la siguiente ecuación:
closeCentrality(x)=(nodes(x,y)/(NodesTotal-1))*(nodes(x,y)/dist(x,y)Total)donde:
- NodesTotal = número de nodos de una red
- nodes(x,y) = número de nodos conectados al nodo x
- dist(x,y)Total = la suma de las distancias de ruta más cortas del nodo x a otros nodos
Centralidad del vector propio
Centralidad del vector propio está basada en nodos importantes que están conectados a otros nodos importantes. Centralidad del vector propio se debería usar cuando se desea determinar qué nodos forman parte de un clúster de influencia. Por ejemplo, un usuario de una red social con muchas conexiones con otros usuarios que tengan muchas conexiones tendrá una centralidad del vector propio mayor que otro usuario con menos conexiones o que esté conectado con usuarios que tengan menos conexiones.
La centralidad del vector propio del nodo x se calcula con la iteración de potencia para encontrar el vector propio más grande mediante la siguiente ecuación:
Ax=λxdonde:
- λ = el valor propio
- x = el vector propio
- A = la matriz que describe la transformación lineal
Peso de eje
Los cálculos para las centralidades de intermediación, cercanía y vector propio se pueden ponderar o no ponderar. Un cálculo de centralidad no ponderada establece los ejes en un peso uniforme con un valor de 1, mientras que un cálculo ponderado utiliza valores de campo para asignar un valor a cada eje.
Nota:
Los pesos no definidos reciben un valor de 1. Se recomienda asignar un campo sin valores nulos o ausentes para el peso de eje.
Para la centralidad del vector propio, los pesos se utilizan para determinar la fortaleza de la conexión entre nodos. Dado que la centralidad del vector propio mide la importancia de los nodos dentro de la red, los valores de peso más altos se corresponden con valores más altos para sus nodos de conexión.
Para las centralidades de cercanía e intermediación, los valores de peso indican la distancia entre nodos. Los pesos de ejes más altos significan una distancia mayor entre nodos y reduce la probabilidad de que se utilice el borde en la ruta más corta. Si un número mayor en el campo de peso deseado indica una mayor importancia (por ejemplo, el número de mensajes enviados entre los miembros de una red social indica cómo son los miembros conectados), se debe calcular un campo nuevo con valores inversos. Utilice la siguiente ecuación para calcular un campo de valores inversos:
weight=ABS(field-MAX(field))+IF(MIN(field)<0, ABS(MIN(field)), MIN(field))Para un cálculo de cercanía o intermediación no ponderada, la ruta más corta es la ruta que utiliza el menor número de vínculos. El siguiente ejemplo muestra una red con cuatro nodos (A, B, C y D) y pesos uniformes. Hay dos rutas que unen el nodo A al nodo D: A-B-D o A-B-C-D. Como A-B-D tiene menos vínculos, es la ruta más corta.

Un cálculo ponderado aplica pesos a cada eje en función de los valores de campo. Las centralidades de cercanía e intermediación ponderadas utilizan el algoritmo Bellman-Ford para buscar las rutas más cortas entre nodos.
El siguiente ejemplo muestra una red con cuatro nodos y ejes ponderados. La ruta A-B-D tiene un valor de 15 y la ruta A-B-C-D tiene un valor de 9. Dado que A-B-C-D tiene el valor de eje más bajo, es la ruta más corta.
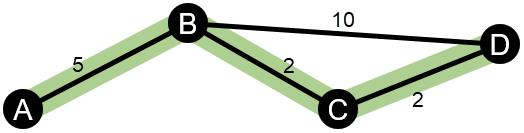
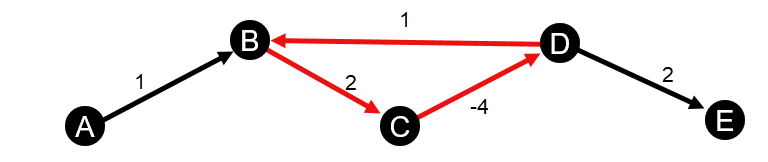
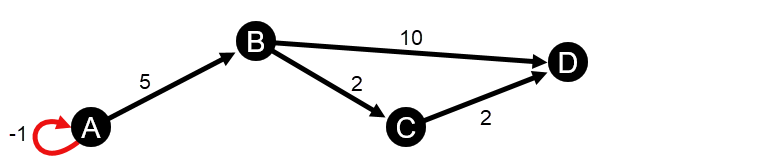
Los cálculos de centralidad de cercanía e intermediación ponderadas no admiten ciclos de peso negativo. Si se detecta un ciclo de peso negativo, todos los valores de centralidad se establecen en 0. Un ciclo de peso negativo se puede dar en las siguientes circunstancias:
- El gráfico contiene un ciclo negativo.
- El gráfico contiene un bucle negativo.
- El gráfico no está direccionado y contiene un eje negativo.
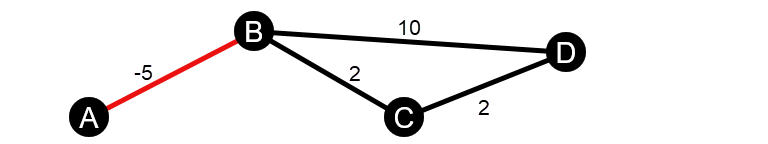
Pasos siguientes
Pruebe estos ejercicios basados en escenarios de Learn ArcGIS para ver flujos de trabajo guiados con análisis de vínculos: