Una vez que se calcula la distancia en línea recta ajustada, puede usar el factor vertical para controlar la velocidad a la que se encuentra la distancia. También puede usar la superficie de coste, las características del elemento en movimiento y el factor horizontal para controlar la velocidad.
El factor vertical explica el esfuerzo para moverse por las pendientes del paisaje. Este esfuerzo afecta a cómo se encuentra la distancia. Ir cuesta arriba puede requerir más esfuerzo, ir cuesta abajo requiere menos esfuerzo y cruzar pendientes representa un punto intermedio. La modificación de la distancia en línea recta ajustada para este esfuerzo ayuda a capturar la velocidad a la que el viajero encuentra la distancia.
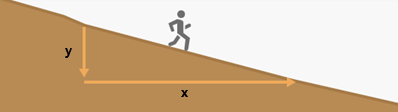
No hay que confundir el factor vertical, que representa el esfuerzo para superar pendientes, con la distancia de la superficie, que es un ajuste de la distancia en línea recta por la distancia real que recorre el viajero a medida que avanza por las subidas y bajadas del paisaje.
La pendiente suele ser relevante para el análisis de coste de distancia. Intuitivamente, es más costoso superar pendientes empinadas que pendientes más planas. Normalmente, la herramienta Parámetros de superficie se utiliza para generar un ráster de pendiente; sin embargo, a veces ese ráster de pendiente se introduce incorrectamente en la superficie de coste.
La opción Pendiente en la herramienta Parámetros de superficie calcula la tasa de cambio de elevación para cada celda del modelo digital de elevación (DEM). Es la primera derivada de un DEM. Pero, como se discutió anteriormente, es importante cómo se encuentra la pendiente cuando se mueve por una celda. El viajero puede evitar una celda asignada a una pendiente pronunciada en una superficie de coste. Esto puede ser efectivo si el viajero se está moviendo cuesta arriba cuando viaja por la celda. Sin embargo, si el viajero se mueve hacia abajo o por esa pendiente cuando se mueve por la celda, se puede preferir la celda para viajar.
Puede tener en cuenta el esfuerzo para superar la pendiente utilizando el ráster de elevación en el factor vertical. No incluya el ráster de pendiente en la superficie de coste cuando la dirección en la que se encuentra la pendiente es importante.
La dirección en la que se calculan las pendientes en el factor vertical también se puede modificar mediante el parámetro de característica de origen Dirección de viaje. Es decir, acercarse o alejarse de un origen cambiará la dirección en la que el viajero entrará en una celda y, como resultado, cómo se encuentra la pendiente.
La incorporación del factor vertical (VF) es un modificador multiplicador de los cálculos de distancia en línea recta ajustada.
Ejemplos de uso del factor vertical
El factor vertical se puede utilizar en varios escenarios, como los siguientes:
- Ubicar una nueva ruta de senderismo entre dos campamentos que sea más larga, pero más fácil de recorrer, que caminar directamente por la ruta más corta entre ellos.
- Examinar los efectos de la sal esparcida por las carreteras en invierno sobre la salud de la vegetación circundante. La vegetación que se encuentra cuesta abajo desde la carretera se verá más afectada por la escorrentía.
- Determinar el movimiento de una criatura marina que depende del cambio en la concentración de salinidad.
Incorporar un factor vertical
El análisis de distancia se puede dividir conceptualmente en las siguientes áreas funcionales relacionadas:
- Calcule la distancia en línea recta y, opcionalmente, ajuste los cálculos con una barrera o un ráster de superficie.
- Una vez que se calcula la distancia en línea recta, determine si lo desea la velocidad a la que se encontrará la distancia a través de una superficie de coste, características del origen, un factor vertical y un factor horizontal. Cree el ráster de distancia acumulada.
- Conecte regiones sobre la superficie de distancia acumulada resultante utilizando una red óptima, rutas específicas o un corredor.
A partir de la segunda área funcional, determine la velocidad a la que se encontrará la distancia a través de un factor vertical como se ilustra a continuación. Este escenario implica un conjunto de cuatro estaciones de guardabosques (puntos morados) y ciertos ríos (líneas azules).
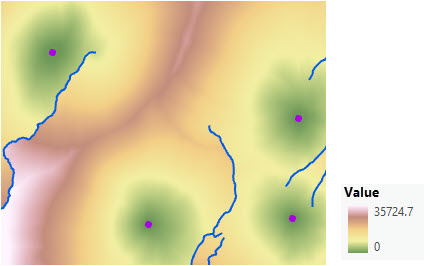
Para incorporar el esfuerzo de los guardabosques para superar las pendientes, se especifica un factor vertical. La superficie de elevación se utiliza como ráster vertical.
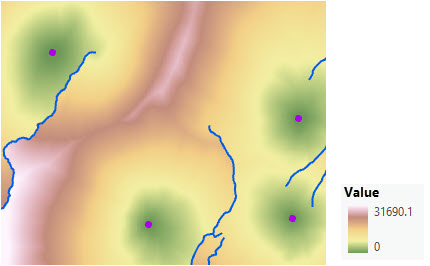
Crear un ráster de distancia usando un factor vertical
Para crear un mapa de distancia que incorpore un factor vertical, siga los pasos siguientes:
- Abra la herramienta Acumulación de distancia.
- Proporcione un origen para el parámetro Ráster o datos de origen de entidad de entrada.
- Asigne un nombre al ráster de acumulación de distancia de salida.
- Expanda la categoría Costes relativos al movimiento vertical.
- Proporcione un ráster de factor vertical para el parámetro Ráster vertical de entrada.
Esta entrada se utiliza para calcular la pendiente que se encuentra al moverse entre celdas. Por lo general, se debe especificar un ráster de elevación.
Aparece el parámetro Factor vertical.
- Especifique la configuración del parámetro Factor vertical.
Este parámetro identifica el multiplicador que se aplicará al coste a ajustar por el esfuerzo de moverse a través de las pendientes encontradas.
- Haga clic en Ejecutar.
El factor vertical afecta la velocidad a la que se encuentra la distancia
Para modificar la velocidad a la que se encuentra la distancia y contabilizar el esfuerzo del viajero para superar pendientes, la herramienta realiza dos acciones de forma interna:
- Calcule cómo se encuentra la pendiente al pasar de una celda a la siguiente. Esto se conoce como el ángulo de movimiento relativo vertical (VRMA).
- Identifique cómo el VRMA modificará la velocidad a la que se encuentra la distancia.
Calcular el VRMA
El VRMA es el ángulo de la pendiente desde la celda de procesamiento (la celda Desde) hasta la celda a la que se mueve el viajero (la celda Hasta). Se calcula la distancia para la celda Hasta. Las alturas a partir de las cuales se calculan las pendientes se definen mediante el ráster de factor vertical de entrada.
La pendiente se calcula utilizando la fórmula del teorema de Pitágoras de la elevación sobre la extensión. La base del triángulo necesaria para determinar la pendiente se deriva de la distancia en línea recta ajustada. La altura se establece al sustraer el valor de la celda de origen del valor de la celda de destino. El ángulo resultante es el VRMA.
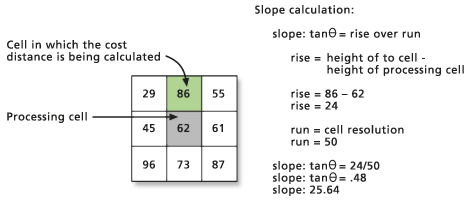
El VRMA se especifica en grados. El rango de valores para el VRMA va desde -90 hasta +90 grados, lo que representa pendientes tanto positivas como negativas.
Identificar el multiplicador VF
El valor del VRMA se traza en el gráfico del factor vertical especificado para obtener el multiplicador del factor vertical que se utilizará en los cálculos que determinan el coste para llegar a la celda de destino. El valor de la distancia para moverse a través de la celda se multiplica por el factor vertical identificado. Mientras más grande sea el factor vertical, más difícil resulta el movimiento. Un VF superior a 1 aumenta el coste de la distancia encontrada. Un VF menor que 1 pero mayor que 0 permite que el elemento en movimiento encuentre las distancias a un ritmo más rápido.
Por ejemplo, el siguiente gráfico muestra la relación del VF y el VRMA para una función de VF lineal:
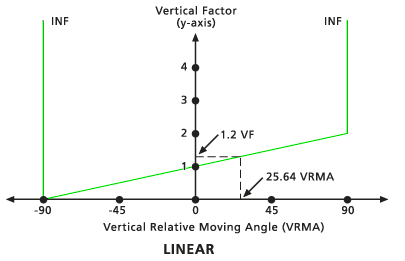
Las funciones de factor vertical que le permiten capturar la interacción del viajero con las pendientes que encuentra son Binaria, Lineal, Lineal inversa, Lineal simétrica, Lineal inversa simétrica, Cos, Sec, Cos-Sec y Sec-Cos. Consulte la sección Información adicional a continuación para obtener detalles de cada función.
Nota:
El factor vertical es un multiplicador. Tenga cuidado al especificar las unidades al combinar el factor vertical con una superficie de coste, características de origen o un factor horizontal. Generalmente, cuando se introduce una superficie de coste, el factor vertical debe ser un ajuste multiplicador de la velocidad de unidades de superficie de coste. Si el tiempo es la unidad para la velocidad de la superficie de coste, el factor vertical debe ser un modificador del tiempo. Solo uno de estos factores puede definir las unidades para la velocidad. Los otros factores no tienen unidades y sus valores son modificadores multiplicadores de las unidades especificadas.
Ejemplos de aplicaciones que utilizan un factor vertical
A continuación se describen ejemplos de aplicaciones que utilizan un factor vertical.
Crear una zona de influencia de pendiente descendente para comprender el efecto de la invernal en la vegetación
Desea identificar las áreas que están cuesta abajo y como máximo a 50 metros de una carretera porque estas áreas pueden verse afectadas por la escorrentía de agua salada en invierno. Desea medir la distancia a lo largo de la superficie del terreno. Puede usar la configuración de factor vertical Binario para evitar que la herramienta Acumulación de distancia identifique celdas más altas que las celdas de carretera. A continuación se muestran ejemplos de las zonas de influencia de pendiente descendente resultantes.
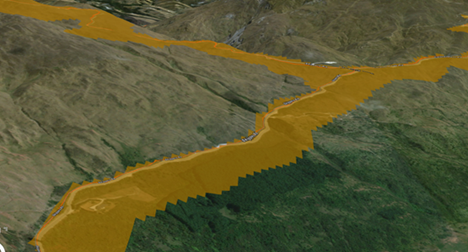
A modo de comparación, a continuación se muestra una sección diferente de la carretera para mostrar la diferencia en las zonas de influencia en línea recta y en las zonas de influencia solo en pendiente descendente.
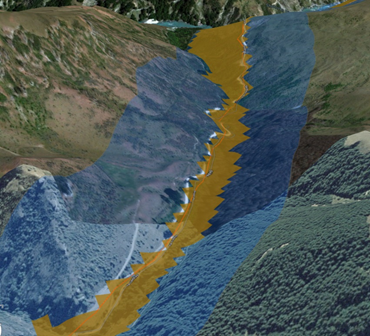
Para crear una zona de influencia de pendiente descendente, siga estos pasos:
- Abra la herramienta Acumulación de distancia.
- Introduzca las carreteras en el parámetro Ráster de entrada o datos de origen de entidades.
- Asigne un nombre al valor Ráster de acumulación de distancia de salida.
- Expanda la categoría Costes relativos al movimiento vertical.
- Proporcione un ráster de elevación en el parámetro Ráster vertical de entrada.
- Establezca Binario para el parámetro Factor vertical.
- Expanda la categoría Características de origen.
- Establezca el parámetro de distancia Acumulación máxima en 50 metros.
- Haga clic en Ejecutar.
Función de senderismo de Tobler
Desea calcular el tiempo de caminata sobre el paisaje, mientras ajusta la velocidad de caminata en función de la pendiente que se encuentra en la dirección del viaje. La función de senderismo de Tobler (1993) es un modelo empírico utilizado para realizar ese ajuste. En el modelo, se supone que la velocidad de marcha base es de 6 km/h, que se alcanza cuando se viaja ligeramente cuesta abajo (alrededor de -3 grados).

Donde S se define en términos de pendiente d (dada en grados), tal que S = tan(d π/180)
La función de velocidad W tiene el siguiente aspecto:
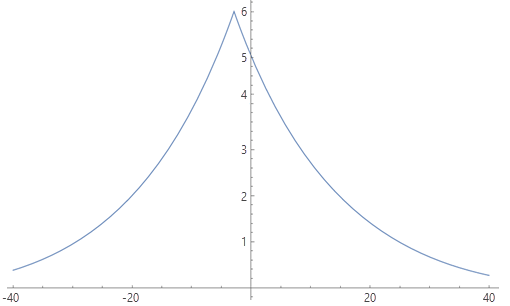
Quiere saber cuánto se tarda en recorrer una distancia determinada (una celda), no qué distancia puede recorrer en un período de tiempo específico, por lo que necesita trabajar con el recíproco de la velocidad, llamado ritmo. El ritmo se expresa en horas por metro (porque las unidades de análisis de la distancia horizontal son metros), en lugar de en horas por kilómetro:
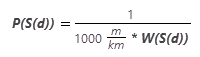
La función de ritmo tiene el siguiente aspecto:
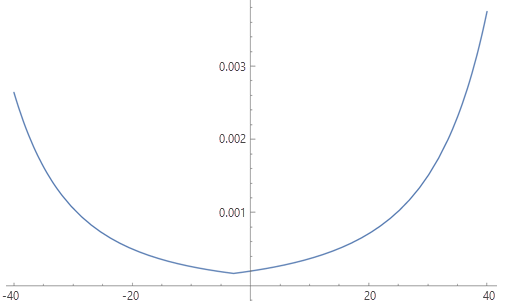
Determine el P(S) para un rango de valores de d y guárdelos en una tabla (que se muestra en la sección Tabla siguiente). Luego, la tabla se puede usar con la función de factor vertical Tabla para proporcionar un coste por celda que tenga en cuenta la dirección de viaje por una celda. El coste (en tiempo) de viajar a través de una celda en una dirección específica y encontrar una pendiente d es P(S(d)) * tamaño de celda (en metros).
Para usar una superficie de fricción de coste de entrada no direccional además de la función de caminata (ritmo) de Tobler en el mismo análisis, preste atención a las unidades de entrada de fricción de coste. En cada celda, la herramienta Acumulación de distancia multiplicará P(S) * (coste de entrada en la celda), por lo que los valores no pueden tener unidades de ritmo. Puede modificar la función de ritmo de Tobler para que sea únicamente un peso (reemplace el 6 con un 1 si cree que está justificado empíricamente) o usar pesos sin unidades en su entrada de costes.
Información adicional
Las siguientes secciones proporcionan información adicional sobre los factores verticales.
Factores verticales
Para definir la función de factor vertical, puede elegir un gráfico de la lista proporcionada o puede crear una función personalizada usando un archivo ASCII. Las siguientes funciones de factor vertical están disponibles en la herramienta Acumulación de distancia:
Opciones de factor vertical, modificadores y valores predeterminados
| Función | Factor cero | Ángulo de corte bajo | Ángulo de corte alto | Pendiente | Potencia | Potencia cos | Potencia sec |
|---|---|---|---|---|---|---|---|
| Binario | 1 | -30 | 30 | N/A | N/A | N/A | N/A |
| Lineal | 1 | -90 | 90 | 1,111E-02 | N/A | N/A | N/A |
| Lineal inverso | 1 | -45 | 45 | -2.222E-02 | N/A | N/A | N/A |
| Lineal simétrico | 1 | -90 | 90 | 1,111E-02 | N/A | N/A | N/A |
| Lineal inverso simétrico | 1 | -45 | 45 | -2.222E-02 | N/A | N/A | N/A |
| Coseno (Cos) | N/A | -90 | 90 | N/A | 1 | N/A | N/A |
| Seg | N/A | -90 | 90 | N/A | 1 | N/A | N/A |
| Cos – Sec | N/A | -90 | 90 | N/A | N/A | 1 | 1 |
| Sec – Cos | N/A | -90 | 90 | N/A | N/A | 1 | 1 |
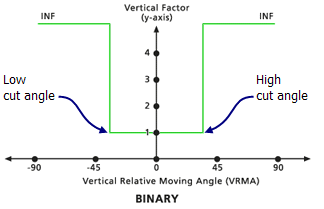
Binario
Cuando el VRMA es mayor que el ángulo de corte bajo y menor que el ángulo de corte alto, el VF para moverse entre las dos celdas se establece en el valor asociado con el factor cero. Si el VRMA es mayor que el ángulo de corte, el VF se establece como infinito. El ángulo de corte predeterminado es de 30 grados, si no se especifica otro.
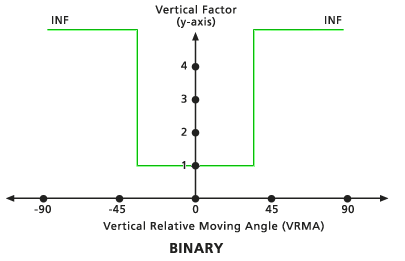
Lineal
Los VF están determinados por una línea recta en el sistema de coordenadas VRMA-VF. La línea intercepta el eje y, equitativo al factor VF, en el valor del factor cero. La pendiente de la línea se puede especificar con el modificador Pendiente. Si no se identifica una pendiente, el valor predeterminado es 1/90 (especificado como 0,01111). El ángulo de corte bajo predeterminado es de -90 grados y el ángulo de corte alto predeterminado es de 90 grados.
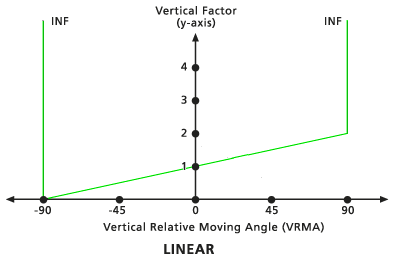
Lineal inverso
Los VF están determinados por los valores inversos de una línea recta en el sistema de coordenadas VRMA-VF. La línea intercepta el eje y, equitativo al factor VF, en el valor del factor cero. La pendiente de la línea se puede identificar si se especifica con el modificador Pendiente. Si no se identifica una pendiente, el valor predeterminado es -1/45 (especificado como 0,02222). El ángulo de corte bajo predeterminado es de -45 grados y el ángulo de corte alto predeterminado es de 45.
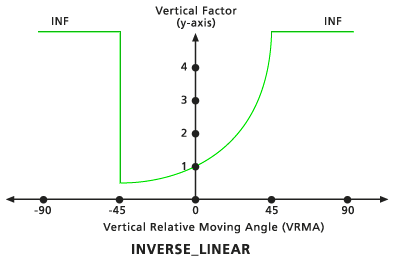
Lineal simétrico
Este factor vertical se compone de dos funciones lineales relativas a los VRMA que son simétricas con respecto al eje VF (y). Ambas líneas interceptan al eje y en el valor VF asociado con el factor cero. La pendiente de las líneas se define como una pendiente única relativa al VRMA positivo mediante el modificador del factor vertical Pendiente, que refleja los VRMA negativos. La pendiente predeterminada es 1/90 (especificada como 0,01111). El ángulo de corte bajo predeterminado es de -90 y el ángulo de corte alto predeterminado es de 90.
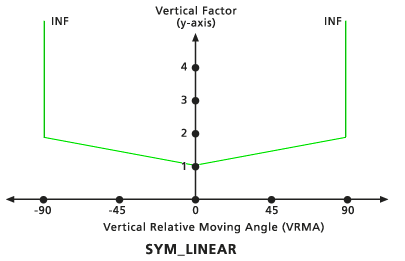
Lineal inverso simétrico
Este factor vertical es el inverso de la palabra clave del factor vertical Lineal simétrico. Comprende dos funciones lineales inversas relativas a los VRMA, que son simétricas al eje VF (y). Ambas líneas interceptan el eje y en el valor VF de 1. La pendiente de las líneas se define como una pendiente única relativa al VRMA positivo mediante el modificador del factor vertical Pendiente, que refleja los VRMA negativos. La pendiente predeterminada es -1/45 (especificada como 0,02222). El ángulo de corte bajo predeterminado es de -45 y el ángulo de corte alto predeterminado es de 45.
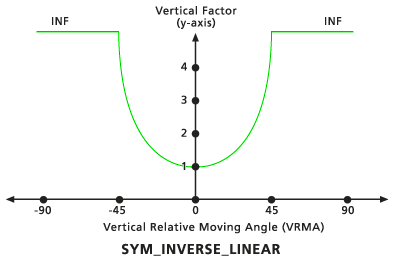
Coseno (Cos)
El VF está determinado por la función coseno del VRMA. El ángulo de corte bajo predeterminado es de -90 grados y el ángulo de corte alto predeterminado es de 90 grados. El valor predeterminado de potencia Cos es 1,0.
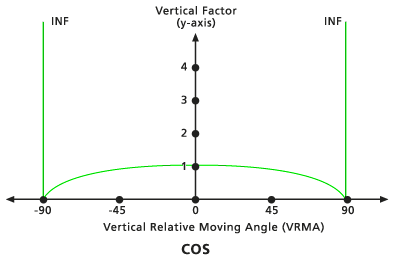
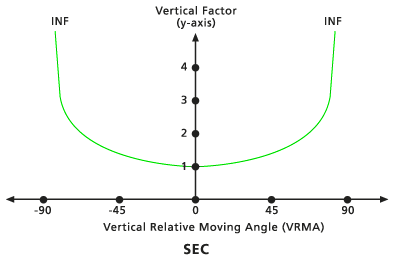
Seg
El VF está determinado por la función secante del VRMA. El ángulo de corte bajo predeterminado es de -90 grados y el ángulo de corte alto predeterminado es de 90 grados. El valor predeterminado de potencia Sec es 1,0.
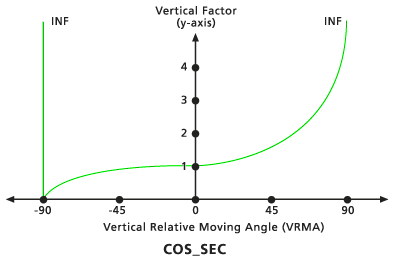
Cos - Sec
Cuando el VRMA es un valor de grado negativo, el VF se determina mediante la función coseno del VRMA. Si el VRMA es un valor de grado positivo, el VF se determina mediante la función secante del VRMA. El ángulo de corte bajo predeterminado es de -90 grados y el ángulo de corte alto predeterminado es de 90 grados. Los valores predeterminados de potencia Cos y potencia Sec son 1,0.
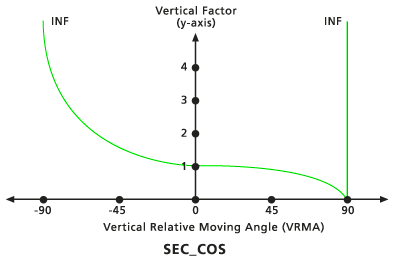
Sec - Cos
Cuando el VRMA es un valor de grado negativo, el VF se determina mediante la función secante del VRMA. Si el VRMA es un valor de grado positivo, el VF se determina mediante la función coseno del VRMA. El ángulo de corte bajo predeterminado es de -90 grados y el ángulo de corte alto predeterminado es de 90 grados. Los valores predeterminados de potencia Sec y potencia Cos son 1,0.
Tabla
La tabla es un archivo ASCII con dos columnas en cada línea.
La primera columna identifica el VRMA en grados y la segunda columna identifica el VF. Cada línea especifica un punto. Dos puntos consecutivos producen un segmento de línea en el sistema de coordenadas VRMA-VF. Los ángulos se deben introducir en orden ascendente y en el rango de -90 a 90. El factor VF para cualquier ángulo VRMA menor que el primer (mínimo) valor de entrada o mayor que la última (máximo) entrada se establecerá como infinito. Un VF infinito se representa con -1 en la tabla ASCII.
La siguiente es una tabla ASCII de factor vertical de ejemplo. Las unidades de la primera columna son grados y las unidades de la segunda columna son horas por metro.
-90 -1
-80 -1
-70 2.099409721
-60 0.060064462
-50 0.009064613
-40 0.00263818
-30 0.001055449
-20 0.000500142
-10 0.00025934
0 0.000198541
10 0.000368021
20 0.000709735
30 0.001497754
40 0.003743755
50 0.012863298
60 0.085235529
70 2.979204206
80 -1
90 -1Modificadores del factor vertical
Puede controlar aún más la función VRMA mediante modificadores que permiten refinar los factores verticales. Puede haber un ángulo de umbral de modo que si el VRMA lo supera, el coste será tan grande que se convertirá en una barrera para el viaje. Este umbral también se conoce como el ángulo de corte. El VF se asigna al infinito cuando el VRMA supera este valor.
El gráfico del factor vertical tendrá un ángulo de corte bajo y un ángulo de corte alto, en contraste con el gráfico del factor horizontal, que solo tendrá un único ángulo de corte.
Con estos modificadores, se pueden especificar ángulos de corte para cada una de las funciones, las curvas trigonométricas se pueden elevar a una potencia, el factor cero puede modificar la intercepción del eje y para las funciones no trigonométricas, y se puede definir la pendiente de la línea en las funciones lineales.
Factor cero
Este modificador establece el factor vertical que será utilizado cuando el VRMA sea cero. Este factor posiciona el interceptor y de la función especificada.
Ángulo de corte bajo
Este modificador es el grado del VRMA que define el umbral más bajo, debajo del cual (menor que) los VF se establecen como el infinito, sin importar las palabras clave del factor vertical especificadas.
Ángulo de corte alto
Este modificador es el grado del VRMA que define el umbral más alto, por encima del cual (mayor que) los VF se establecen como infinito, sin importar las palabras clave del factor vertical especificadas.
Pendiente
Este modificador identifica la pendiente de las líneas rectas en el sistema de coordenadas VRMA-VF para las palabras clave Lineal, Lineal inverso, Lineal simétrico y Lineal inverso simétrico. La pendiente está especificada como la elevación sobre la extensión (por ejemplo, una pendiente de 30 grados es 1/30, especificada como 0,03333). Consulte el diagrama VRMA lineal para obtener un ejemplo de una función lineal con una pendiente de 1/90.
Potencia
Este modificador es la potencia a la que se elevarán los valores.
Potencia cos
Este modificador es la potencia a la que se elevarán los valores no negativos de la función VRMA Sec-Cos y los valores negativos de la función VRMA Cos-Sec. El VF está determinado por lo siguiente:
VF = potencia cos(VRMA)Potencia sec
Este modificador es la potencia a la que se elevarán los valores no negativos de la función VRMA Cos-Sec y los valores negativos de la función VRMA Sec-Cos. El VF está determinado por lo siguiente:
VF = potencia sec(VRMA)Nombre de tabla
Este modificador identifica el nombre del archivo ASCII que se utilizará con la palabra clave del factor vertical Tabla.
Referencias
Tobler, Waldo (1993) Tres presentaciones sobre análisis y modelado geográfico: modelado geográfico no isotrópico, especulaciones sobre la geometría de la geografía y análisis espacial global (93-1) Obtenido de https://escholarship.org/uc/item/05r820mz