正如通过在地图上绘制要素您可以感受到要素的方向性一样,计算标准差椭圆则可使这种趋向变得更为明确。您可以根据要素的位置点或受与要素关联的某个属性值影响的位置点来计算标准差椭圆。后者称为加权标准差椭圆。
计算
标准差椭圆如下所示:
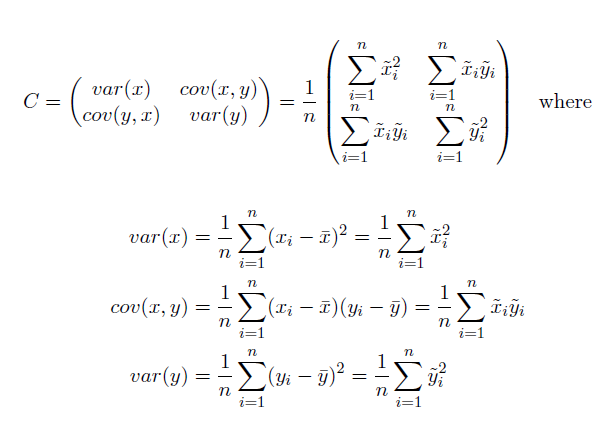
其中 x 和 y 是 i要素的坐标,{x̄, ȳ} 表示要素的平均中心,n 为要素总数。
样本协方差矩阵被分解为标准形式,使得矩阵可由本征值和特征向量来表示。于是,x 和 y 轴的标准差为:
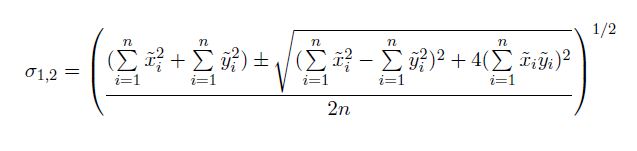
如果您想了解更多关于本征值和特征向量的内容,请查阅 其他资源。
输出和解释
对于二维数据来说,方向分布(标准差椭圆)工具会创建一个新要素类,其中包含一个以所有要素的平均中心为中心的椭圆面(或如果为案例分组字段指定了值,则为所有案例)。这些输出椭圆面的属性值包括两个标准距离(长轴和短轴)、椭圆的方向和案例分组字段(如指定)。方向表示从顶点开始按顺时针进行测量的长轴的旋转。您还可以指定要表示的标准差数(1、2 或 3)。
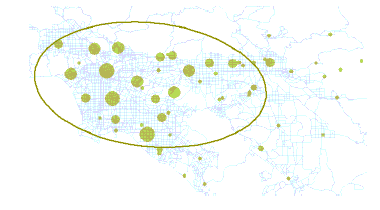
潜在的应用
- 在地图上标示一组犯罪行为的分布趋势可以确定该行为与特定要素(一系列酒吧或餐馆、某条特定街道等)的关系。
- 在地图上标示地下水井样本的特定污染可以指示毒素的扩散方式,这在部署减灾策略时非常有用。
- 对各个种族或民族所在区域的椭圆的大小、形状和重叠部分进行比较可以提供与种族隔离或民族隔离相关的深入信息。
- 绘制一段时间内疾病爆发情况的椭圆可建立疾病传播的模型。
- 当调查大气状况和飞行事故间的关联时,检查某一类暴风的高程分布是需要考虑的一个有用因素。
其他资源
Chew, Victor. "Confidence, prediction, and tolerance regions for the multivariate normal distribution." Journal of the American Statistical Association 61.315 (1966): 605-617.
Fisher, N. I., T. Lewis, and B. J. J. Embleton. Statistical Analysis of Spherical Data. 1st ed. Cambridge: Cambridge University Press, 1987. Cambridge Books Online. Web. 26 April 2016.
Levine, Ned. "CrimeStat III: a spatial statistics program for the analysis of crime incident locations (version 3.0)." Houston (TX): Ned Levine & Associates/Washington, DC: National Institute of Justice (2004).
Mitchell, Andy. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
Wang, Bin, Wenzhong Shi, and Zelang Miao. (2015) Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space. PLoS ONE 10(3), e0118537.