块统计的工作原理

块统计工具所执行的运算可为一组固定的非重叠窗口或邻域中的输入像元计算统计数据。 为每个邻域中包含的所有输入像元计算统计数据（例如，平均值、最大值或总和）。 将单个邻域或块的结果值分配给包含在指定邻域的最小边界矩形中的所有像元位置。

邻域处理

从概念上讲，对于每个像元块，该算法都会计算落在该块中指定邻域形状内的输入像元的统计数据。 由于邻域不重叠，因此所有特定输入像元将仅包含在一个块的计算中。

有多种预定义的邻域形状可供选择。 您还可以创建自定义形状。 可以对邻域计算得出的统计数据包括众数、最大值、平均值、中值、最小值、少数、范围、标准差、总和及变异度。

从概念上讲，块统计工具的工作原理如下：

• 在分析窗口的左上角创建第一个指定的邻域，例如圆形邻域。

  

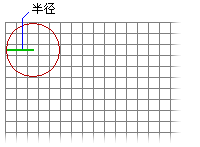
• 计算最小外接矩形以确定输出块的大小。

  

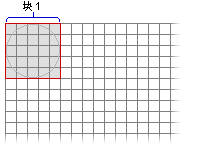
• 将栅格的其余区域分成多个已定义的块。 块不能叠置。

  

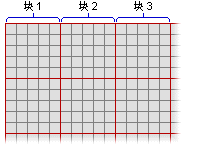
• 在每个块中识别块计算将要使用的像元位置。 像元位置由适合边界矩形的指定邻域（例如圆形邻域）定义确定。

  

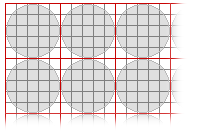
• 为每个块的各个邻域计算输出值。 将结果值分配给对应输出块中的各个像元。

NoData 像元

在计算中忽略 NoData 参数可控制邻域窗口内 NoData 像元的处理方式。 选中此参数（Python 中的 ignore_nodata = "DATA"）时，块输出值的计算将会忽略邻域中的所有 NoData 像元。 取消选中此参数（Python 中的 ignore_nodata = "NODATA"）时，如果邻域中存在任何 NoData 像元，则输出块中的所有像元都将为 NoData。

邻域大小

邻域在任何维度上的最大大小限制为 2,048 个像元。 这意味着矩形邻域在水平或垂直方向上都不能超过这个数量的像元。 对于圆形邻域，半径不能超过 1,023 个像元。

邻域类型

邻域可以是环形（圆环）、圆形、矩形或楔形。 通过使用核文件，也可自定义邻域形状，以及在计算统计数据之前将不同的权重分配给邻域中的各个特定像元。

以下是不同邻域形状的描述及其定义方法：

• 环形
  • 环由两个圆组成，一个圆位于另一个圆的内侧，从而构成圆环。 邻域处理中将包括中心位于较小圆半径和较大圆半径之间的像元。 处于两个圆形之间的区域构成环形邻域。
  • 半径以像元或地图单位为单位，并沿垂直于 x 轴或 y 轴的方向进行测量。 当半径以地图单位指定时，其将转换为以像元为单位的半径。 所得的以像元为单位的半径会生成一个区域，该区域能够近似地表示出以原始的地图单位为半径时计算的区域。 在邻域处理中将包含环涵盖的所有像元中心。
  • 默认环形邻域具有一个像元的内半径以及三个像元的外半径。
  • 以下为环形邻域的示例图：

  

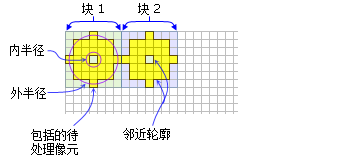
  显示了具有默认环形邻域的两个处理块（内半径 = 1 像元，外半径 = 3 像元）。

• 圆形
  • 通过指定半径值来创建圆形邻域。
  • 半径以像元或地图单位为单位，并沿垂直于 x 轴或 y 轴的方向进行测量。 当半径按地图单位指定时，会使用附加逻辑条件来确定在处理邻域时要包含的像元。 首先，计算由指定半径值定义的圆的精确面积。 然后，再计算出另外两个圆面积值，一个是指定半径值向下舍入后的圆面积，另一个是指定半径值向上舍入后的圆面积。 这两个面积分别与用指定半径计算出的准确面积值进行比较，更为接近准确面积值的半径将被用于运算过程中。
  • 默认圆形邻域半径为三个像元。
  • 以下为圆形邻域的示例图：

  

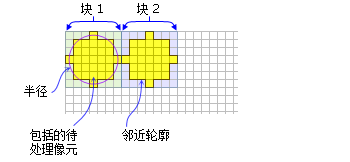
  显示了具有默认圆形邻域的两个处理块（半径 = 3 像元）。

• 矩形
  • 通过提供以像元或地图单元为单位的宽度和高度值，指定矩形邻域。
  • 仅将中心在定义对象内的像元作为矩形邻域的一部分进行处理。
  • 默认矩形邻域为高和宽为三个像元的正方形。
  • 以下为矩形邻域的示例图：

  

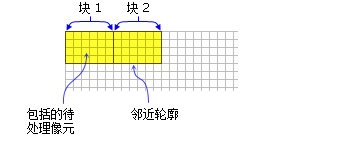
  显示了具有矩形邻域的两个处理块（宽度 = 6 像元，高度 = 4 像元）。

• 楔形
  • 楔形是由半径、起始角度和终止角度指定的饼形邻域。
  • 楔形按逆时针方向从起始角延伸到终止角。 角度以 0 到 360 的算术角度指定，其中 0 位于正 x 轴（3 点钟方向），并且可以是整数或浮点数。 也可使用负角度。
  • 半径以像元或地图单位为单位，并沿垂直于 x 轴或 y 轴的方向进行测量。 当半径以地图单位指定时，其将转换为以像元为单位的半径。 所得的以像元为单位的半径会生成一个区域，该区域能够近似地表示出使用原始的地图单位为半径时计算的区域。 在邻域处理中将包含楔形涵盖的所有像元中心。
  • 默认楔形邻域起始角度为 0 度，终止角度为 90 度，半径为三个像元。
  • 以下为楔形邻域的示例图：

  

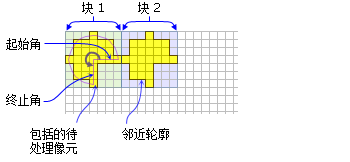
  显示了具有楔形邻域的两个处理块（半径 = 3 像元，起始角 = 0，终止角 = 270）。

• 不规则
  • 允许您指定形状不规则的邻域。
  • 不规则核文件可指定要包含在邻域范围内的像元位置。
  • 以下内容适用于不规则邻域的核文件：
    • 不规则的核文件是一种 ASCII 文本文件，用于定义不规则邻域的值和形状。 可以使用任何文本编辑器来创建此文件。 其必须具有文件扩展名 .txt。
    • 第一行用于指定邻域的宽度和高度（x 方向的像元数，后跟一个空格，y 方向的像元数）。
    • 随后几行定义了用于其所代表邻域中每个位置的值。 各值之间需要添加一个空格。
    • 这些值定义了是否将邻域中的位置包括在计算中。 通常，值 1 用于标识要包含在不规则邻域计算中的位置，但可以使用除 0 以外的任何正值或负值。 也可以使用浮点值。
    • 要从计算中排除邻域中的位置，需在核文件中的相应位置使用值 0（不是空格）。

  • ASCII 不规则核文件及其所表示的邻域的示例如下：

  

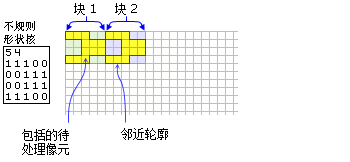
  显示了一个不规则邻域核，以及将包含两个块中要处理像元的图示。

• 权重
  • 与不规则邻域类型相似，权重邻域用于定义不规则形状邻域，此外还可以指定各输入值的权重。
  • 权重核文件可指定要包含在邻域范围内的像元位置及其权重。
  • 权重邻域仅适用于平均值、标准差和总和统计类型。
  • 以下内容适用于权重邻域的核文件：
    • 加权核文件是一种 ASCII 文本文件，用于定义加权邻域的值和形状。 可以使用任何文本编辑器来创建此文件。 其必须具有文件扩展名 .txt。
    • 第一行用于指定邻域的宽度和高度（x 方向的像元数，后跟一个空格，y 方向的像元数）。
    • 随后几行定义了用于其所代表邻域中每个位置的值。 各值之间需要添加一个空格。
    • 对于总和统计数据，权重可以是任何正负整数值或浮点值。
    • 对于平均值和标准差统计数据，权重可以是任何正整数值或浮点值。 这些统计数据不允许使用负值，因此在计算中将忽略任何具有负权重的位置。
    • 要从计算中排除邻域中的位置，需在核文件中的相应位置使用值 0（不是空格）。

  • 加权核文件的内容及其所表示的邻域的示例如下：

  

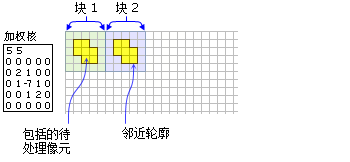
  显示了一个加权邻域核，以及将包含两个块中要处理像元的图示。

统计类型

可用的统计数据包括众数、最大值、平均值、中值、最小值、少数、范围、标准差、总和及变异度。 默认统计类型为平均值。

• 众数
  • 仅可将整型栅格用作输入。
  • 应确定每个块邻域中每个唯一像元值的频率。 如果存在具有最高频率（出现频率最高）的单个值，则该值将分配给该邻域中的所有像元。 如果存在平局，则分配最低的平局值。
• 最大值
  • 如果输入栅格值为整型，则输出栅格中的值也将为整型；如果输入栅格值为浮点型，则输出栅格中的值也将为浮点型。
• 平均值
  • 输入可以是整型或浮点型栅格。
  • 输出栅格值始终为浮点型。
  • 对于权重邻域类型，此为受支持的统计数据类型子集。 有关如何计算此统计数据的详细信息，请参阅加权邻域部分。
• 中值
  • 仅可将整型栅格用作输入。
  • 如果邻域中有效像元值数量为奇数，则将排列这些值然后选择位于中间的值得到中值。 如果邻域中值的数目为偶数，则将对这些值进行排列，并从两个中间值中选择较低的值。
• 最小值
  • 如果输入栅格值为整型，则输出栅格中的值也将为整型；如果输入栅格值为浮点型，则输出栅格中的值也将为浮点型。
• 少数
  • 仅可将整型栅格用作输入。
  • 应确定每个块邻域中每个唯一像元值的频率。 如果存在具有最低频率（出现频率最低）的单个值，则该值将分配给该邻域中的所有像元。 如果存在平局，则分配最低的平局值。
• 范围
  • 如果输入栅格值为整型，则输出栅格中的值也将为整型；如果输入栅格值为浮点型，则输出栅格中的值也将为浮点型。
  • 通过应用以下这个简单的公式可逐个像元地确定输出栅格中各个像元位置上的值：Block Range = Block Maximum – Block Minimum。
• 标准差
  • 输出栅格值始终为浮点型。
  • 对于权重邻域类型，此为受支持的统计数据类型子集。 有关如何计算此统计数据的详细信息，请参阅加权邻域部分。
  • 标准差是在整个总体（N 方法）上计算求得，而不是在样本（N-1 方法）上进行估算。
• 总和
  • 如果输入栅格值为整型，则输出栅格中的值也将为整型；如果输入栅格值为浮点型，则输出栅格中的值也将为浮点型。
  • 对于权重邻域类型，此为受支持的统计数据类型子集。 有关如何计算此统计数据的详细信息，请参阅加权邻域部分。
• 变异度
  • 仅可将整型栅格用作输入。

加权邻域计算

可以通过应用权重来调整邻域中每个值对处理块的最终结果的影响量。

在以下部分中，将显示用于计算加权平均值、标准差和总和统计数据结果的公式。 均附带一个示例，显示处理块的计算和 3 x 3 像元矩形邻域的结果。

加权平均数统计

对于具有平均统计数据的权重邻域，处理块中像元的输出值是核权重值乘以输入值的乘积之和，再除以核权重值之和。

应用于邻域内像元的公式如下：

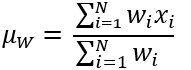
其中：

• µ_W 是处理区块的人口加权平均值。
• N 是邻域中的像元数。
• w_i 是在核中定义的权重值。
• x_i 是输入像元值。

旧版本：

在以前的版本中，计算使用邻域中的像元数作为分母。

权重值必须为正值，可以是整数值或浮点值。

示例

考虑以下 3 x 3 矩形输入像元块：

4 6 7 6 7 8 4 5 6

这些值的数学平均值（总和/计数）为 53 / 9 = 5.889。

考虑以下 3 x 3 加权像元核：

3 3 0.0 0.5 0.0 0.5 2.0 0.5 0.0 0.5 0.0

该核对块中的中心像元的影响程度最高（权重为 2），四个正交相邻像元对中心像元的影响较小（权重为 0.5），四个角像元对处理像元没有影响（权重为 0）。

应用上面提供的加权平均数等式，下面显示了获取最终值的计算。

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) / (w1 + w2 + w3 + w4 + w5 + w6 + w7 + w8 + w9) = ((0*4)+(0.5*6)+(0*7)+(0.5*6)+(2.0*7)+(0.5*8)+(0*4)+(0.5*5)+(0*6)) / (0+0.5 + 0 + 0.5 + 2.0 + 0.5 + 0 + 0.5 + 0) = (0 + 3.0 + 0 + 3.0 + 14.0 + 4.0 + 0 + 2.5 + 0) / (0.5 + 0.5 + 2.0 + 0.5 + 0.5) = (3.0 + 3.0 + 14.0 + 4.0 + 2.5) / 4.0 = 26.5 / 4.0 = 6.625

作为比较，九个输入像元的常规平均值为 5.889。 如果只包括核中的五个输入像元（其中权重 ！ = 0），但不考虑权重值，则平均值将为 6.4（6 + 6 + 7 + 8 + 5 = 32，当将其除以计数 5 时）。

加权标准差统计

对于具有标准差统计数据的权重邻域，处理块中像元的输出值是以下等式的结果：

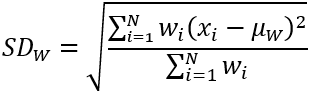
其中：

• SD_W 是处理区块的人口加权标准差值。
• µ_W 是处理区块的人口加权平均值。
• N 是邻域中的像元数。
• w_i 是在核中定义的权重值。
• x_i 是输入像元值。

权重值必须为正值，可以是整数值或浮点值。

如果邻域中的所有输入值都相同，则该处理块中像元的标准差值为 0。

示例

在此示例中将再次使用上述加权平均值示例中使用的相同邻域值。

4 6 7 6 7 8 4 5 6

还将使用相同的加权核值：

3 3 0.0 0.5 0.0 0.5 2.0 0.5 0.0 0.5 0.0

应用上面提供的像元块的加权标准差等式，计算结果约为 0.85696。 该值将被写入该块邻域中的每个像元。

加权总和统计

对于具有总和统计数据的权重邻域，处理块中像元的输出值是以下等式的结果：

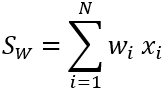
其中：

• S_W 是处理区块的加权总和值。
• N 是邻域中的像元数。
• w_i 是在核中定义的权重值。
• x_i 是输入像元值。

权重值可以为正值或负值，可以是整数值或浮点值。

示例

考虑以下邻域输入值：

4 6 7 6 7 8 4 5 6

考虑以下 3 x 3 加权像元核：

3 3 -1 -2 -1 0 0 0 1 2 1

应用上面提供的等式，下面显示了获取最终值时使用的计算：

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) = ((-1*4) + (-2*6) + (-1*7) + (0*6) + (0*7) + (0*8) + (1*4) + (2*5) + (1*6)) = (-4) + (-12) + (-7) + 4 + 10 + 6 = -3