


Analiza połączeń to technika analityczna skupiająca się na relacjach i połączeniach w obrębie zestawu danych. Analiza połączeń umożliwia obliczanie miar centralności — a konkretnie centralności stopniowej, międzywęzłowej, bliskości i wektora własnego — oraz wyświetlanie połączeń na diagramie połączeń lub mapie połączeń.
Informacje na temat analizy połączeń
Funkcja analizy połączeń umożliwia identyfikowanie i analizowanie relacji, które trudno dostrzec w nieprzetworzonych danych, wykorzystując do tego sieć wzajemnych połączeń. Oto popularne rodzaje sieci:
- Sieci społecznościowe, w których użytkownicy rozmawiają ze sobą
- Sieci semantyczne przedstawiające powiązane ze sobą tematy
- Sieci konfliktów przedstawiające sojusze i połączenia między graczami
- Sieci lotnicze przedstawiające połączenia między lotniskami
Przykłady
Analityk kryminalny rozpracowuje siatkę przestępczą. Na podstawie danych operatora komórkowego określa relacje i hierarchię pomiędzy członkami tej sieci.
Operator kart kredytowych tworzy nowy system wykrywania kradzieży kart. Na podstawie znanych wzorców transakcji poszczególnych klientów (miasto, sklepy, rodzaje transakcji) system wykrywa anomalie i alarmuje klienta o potencjalnej kradzieży.
Analityk służby zdrowia prowadzi badania nad nadużywaniem opiatów w Ameryce Północnej. Na podstawie danych recept i danych demograficznych określa nowe wzorce pojawiające się w miarę rozwoju zjawiska.
Jak działa analiza połączeń
Poniższa tabela zawiera podstawowe terminy używane w analizie połączeń:
| Okres ważności | Opis | Przykłady |
|---|---|---|
Sieć | Zbiór wzajemnie powiązanych węzłów i połączeń. | Internetowa sieć społecznościowa, w której użytkownicy są połączeni w ramach sieci profili i relacji. Sieci lotnicze stanowiące rozbudowany układ lotnisk i lotów, umożliwiające transport pasażerów z lokalizacji źródłowych do docelowych. |
Węzeł | Punkt lub wierzchołek reprezentujący obiekt, na przykład osobę, miejsce, przestępstwo lub tweet. Z węzłem mogą być także powiązane właściwości. | Profile w sieci społecznościowej. Powiązanymi właściwościami mogą być nazwa, miasto lub pracodawca użytkownika. Lotniska w sieci lotniczej. Powiązaną właściwością może być nazwa lotniska. |
Link | Relacje lub połączenia między węzłami. Z połączeniem mogą być także powiązane właściwości. | Relacje między profilami w sieci, na przykład znajomy, obserwujący lub kontakt. Powiązaną właściwością może być długość relacji. Loty między lotniskami w sieci lotniczej. Powiązaną właściwością może być liczba lotów między lotniskami. |
Położenie centralne
Centralność jest miarą istotności węzłów w sieci.
Centralność ogólna służy do następujących celów:
- Ocena wpływu węzła na inne węzły w sieci. Na przykład: który użytkownik dotrze do największej liczby innych użytkowników, gdy udostępni wiadomość lub ofertę pracy?
- Określenie węzłów będących pod największym wpływem innych węzłów. Na przykład: które lotnisko zostanie w największym stopniu dotknięte skutkami odwołania lotów w wyniku burzy w innym regionie?
- Obserwacja przepływu lub rozprzestrzeniania czegoś w sieci (informacji, obiektów, zjawisk itp.). Na przykład: jak wygląda droga paczki z magazynu do miejsca doręczenia?
- Analiza skuteczności rozprzestrzeniania zjawisk w sieci przez poszczególne węzły. Na przykład: z którą redakcją (gazety lub kanału telewizyjnego) należy się skontaktować, aby wiadomość dotarła do największej liczby osób?
- Określanie węzłów umożliwiających blokowanie lub zapobieganie rozprzestrzenianiu zjawisk. Na przykład: gdzie powinny być rozmieszczone punkty szczepień, aby powstrzymać rozprzestrzenianie się wirusa?
W aplikacji Insights istnieją cztery rodzaje miary centralności: centralność stopniowa, centralność międzywęzłowa, centralność bliskości oraz centralność wektora własnego.
Obliczenia centralności międzywęzłowej, bliskości i wektora własnego mogą być ważone lub nieważone.
Centralność stopniowa
Centralność stopniowa zależy od liczby bezpośrednich połączeń węzła. Należy jej używać do określania węzłów o największym wpływie bezpośrednim. Na przykład w sieci społecznościowej najwyższą wartość centralności stopniowej będą mieli użytkownicy o największej liczbie połączeń bezpośrednich.
Centralność stopniową węzła x można obliczyć przy użyciu następującego równania:
degCentrality(x)=deg(x)/(NodesTotal-1)gdzie:
- WęzłySuma = liczba węzłów w sieci
- deg(x) = liczba węzłów połączonych z węzłem x
W przypadku połączeń kierunkowych, czyli gdy informacje przepływają między węzłami tylko w jednym kierunku, centralność stopniową można mierzyć w stopniach wewnętrznych lub w stopniach zewnętrznych. W sieci społecznościowej wartość stopni wewnętrznych będzie zależna od liczby profili obserwowanych przez użytkownika, a wartość stopni zewnętrznych — od liczby osób obserwujących profil użytkownika.
Centralność stopniową wewnętrzną można obliczyć przy użyciu następującego równania:
indegCentrality(x)=indeg(x)/(NodesTotal-1)gdzie:
- WęzłySuma = liczba węzłów w sieci
- indeg(x) = liczba węzłów połączonych z węzłem x, gdy przepływ jest skierowany do węzła x
Centralność stopniową zewnętrzną można obliczyć przy użyciu następującego równania:
outdegCentrality(x)=outdeg(x)/(NodesTotal-1)gdzie:
- WęzłySuma = liczba węzłów w sieci
- outdeg(x) = liczba węzłów połączonych z węzłem x, gdy przepływ jest skierowany od węzła x
W przypadku grafów skierowanych aplikacja Insights domyślnie określa rozmiar węzłów według centralności stopniowej zewnętrznej.
Centralność międzywęzłowa
Centralność międzywęzłowa zależy od zasięgu przynależności węzła do najkrótszej ścieżki między innymi węzłami. Należy jej używać do określania węzłów służących do nawiązywania połączeń z innymi węzłami. Na przykład użytkownik w sieci społecznościowej mający połączenia z wieloma grupami znajomych będzie miał wyższą wartość centralności międzywęzłowej niż użytkownicy z połączeniami z zaledwie jedną grupą.
Centralność międzywęzłową węzła x można obliczyć przy użyciu następującego równania:
btwCentrality(x)=Σa,bϵNodes(pathsa,b(x)/pathsa,b)gdzie:
- Węzły = wszystkie węzły w sieci
- pathsa,b = liczba najkrótszych ścieżek między wszystkimi węzłami a i b
- pathsa,b(x) = liczba najkrótszych ścieżek między węzłami a i b przebiegających przez węzeł x
W powyższym równaniu nie uwzględniono rozmiaru sieci, dlatego w dużych sieciach wartości centralności międzywęzłowej będą większe niż w małych sieciach. Aby można było porównywać sieci o różnych rozmiarach, równanie centralności międzywęzłowej musi zostać znormalizowane, czyli podzielone przez liczbę par węzłów na diagramie.
Oto równanie normalizujące diagram nieukierunkowany:
1/2(NodesTotal-1)(NodesTotal-2)gdzie:
- WęzłySuma = liczba węzłów w sieci
Oto równanie normalizujące diagram ukierunkowany:
(NodesTotal-1)(NodesTotal-2)gdzie:
- WęzłySuma = liczba węzłów w sieci
Centralność bliskości
Centralność bliskości jest zależna od średniej wartości najkrótszej ścieżki między węzłami w sieci. Należy jej używać do określania węzłów najbliżej powiązanych z innymi węzłami w sieci. Na przykład użytkownik z większą liczbą bezpośrednich połączeń w sieci społecznościowej będzie miał wyższą wartość centralności bliskości niż użytkownik z połączeniami pośrednimi (czyli tzw. znajomy znajomych).
Notatka:
Odległość między węzłami oznacza liczbę połączeń między nimi, nie odległość geograficzną.
Centralność bliskości węzła x można obliczyć przy użyciu następującego równania:
closeCentrality(x)=(nodes(x,y)/(NodesTotal-1))*(nodes(x,y)/dist(x,y)Total)gdzie:
- WęzłySuma = liczba węzłów w sieci
- nodes(x) = liczba węzłów połączonych z węzłem x
- dist(x,y)Suma = suma wartości najkrótszych ścieżek między węzłem x, a innymi węzłami
Centralność wektora własnego
Centralność wektora własnego zależy od ważnych węzłów łączonych z innymi ważnymi węzłami. Centralności wektora własnego należy używać do określania węzłów należących do klastra oddziaływania. Na przykład użytkownik w sieci społecznościowej mający wiele połączeń z innymi użytkownikami o wielu połączeniach będzie mieć wyższą wartość centralności wektora własnego od użytkownika mającego niewiele połączeń lub połączonego z innymi użytkownikami o niewielu połączeniach.
Centralność wektora własnego węzła x jest obliczana za pomocą metody power iteration (powtarzanie potęgowania) w celu znalezienia największego wektora własnego z użyciem następującego równania:
Ax=λxgdzie:
- λ = wartość własna
- x = wektor własny
- A = macierz opisująca transformację liniową
Waga segmentu
Obliczenia centralności bliskości, międzywęzłowej i wektora własnego mogą być ważone lub nieważone. Nieważone obliczenie centralności nadaje segmentom jednolitą wagę o wartości 1, a obliczenie ważone korzysta z wartości pól w celu przypisania wartości do poszczególnych segmentów.
Notatka:
Niezdefiniowanym wagom jest przypisywana wartość 1. Zalecane jest przypisywanie jako wag segmentów pól zawierających wartości inne niż NULL.
W przypadku centralności wektora własnego wagi służą do określenia siły połączenia między węzłami. Ponieważ centralność wektora własnego mierzy istotność węzłów w sieci, wyższe wartości wag odpowiadają wyższym wartościom ich połączonych węzłów.
W przypadku centralności bliskości i międzywęzłowej wartości wag wskazują odległość między węzłami. Wyższe wagi segmentów oznaczają większą odległość między węzłami i zmniejszają prawdopodobieństwo użycia segmentu w najkrótszej ścieżce. Jeśli wyższa liczba w polu preferowanej wagi wskazuje zwiększoną ważność (na przykład liczba wiadomości wysłanych między członkami sieci społecznościowej wskazuje, w jaki sposób są połączeni), nowe pole musi zostać obliczone z odwrotnymi wartościami. Aby obliczyć pole odwróconych wartości, użyj następującego równania:
waga=ABS(pole-MAX(pole))+IF(MIN(pole)<0, ABS(MIN(pole)), MIN(pole))W przypadku obliczeń nieważonej centralności bliskości lub międzywęzłowej najkrótsza ścieżka to taka, która wykorzystuje najmniejszą liczbę łączy. W poniższym przykładzie przedstawiona została sieć z czterema węzłami (A, B, C i D) oraz jednolitymi wagami. Istnieją dwie ścieżki łączące węzeł A z węzłem D: A-B-D lub A-B-C-D. Ponieważ A-B-D ma mniej łączy, jest to najkrótsza ścieżka.

Obliczenie ważone stosuje wagi do każdego segmentu na podstawie wartości pól. W ważonych centralnościach bliskości i międzywęzłowych do znalezienia najkrótszych ścieżek między węzłami jest używany algorytm Bellmana-Forda.
W poniższym przykładzie przedstawiona została sieć z czterema węzłami i ważonymi segmentami. Ścieżka A-B-D ma wartość 15, a ścieżka A-B-C-D ma wartość 9. Ponieważ A-B-C-D ma niższą wartość segmentu, jest to najkrótsza ścieżka.
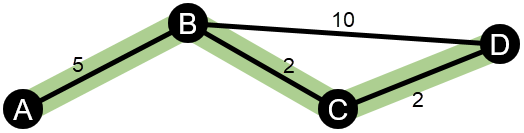
W obliczeniach ważonych centralności bliskości i międzywęzłowej nie są obsługiwane ujemne cykle wag. Jeśli zostanie wykryty ujemny cykl wag, wszystkie wartości centralności zostaną ustawione na 0. Ujemny cykl wag może wystąpić w następujących okolicznościach:
- Wykres zawiera ujemny cykl.
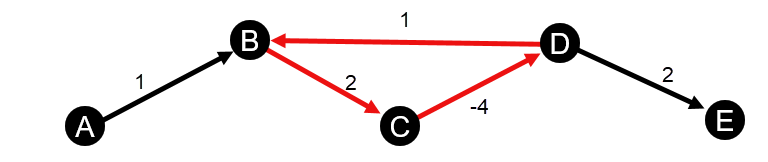
- Wykres zawiera ujemną pętlę własną.
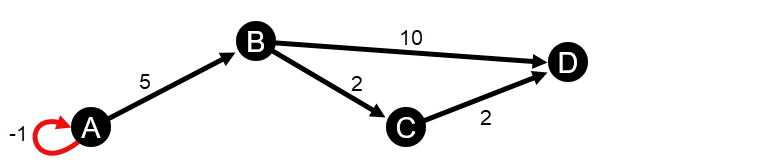
- Wykres jest nieskierowany i zawiera ujemny segment.
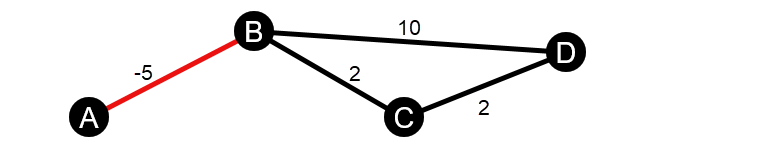
Kolejne etapy
Wypróbuj następujące ćwiczenia oparte na scenariuszach znajdujące się w temacie Naucz się korzystać z oprogramowania ArcGIS i zawierające procedury wykonywania zadań z przewodnikiem oraz analizę łączy: