


링크 분석은 데이터셋의 연결 및 관계에 중점을 둔 기술입니다. 링크 분석을 통해 중심성 측정(즉, 정도, 매개성, 인접성, 고유 벡터)을 계산하고 링크 차트 또는 링크 맵 상의 연결을 시각화할 수 있습니다.
링크 분석은 원시 데이터로는 쉽게 확인할 수 없는 관계를 상호 연결된 링크 및 노드 네트워크를 사용하여 식별하고 분석합니다. 일반적인 네트워크 유형에는 다음이 포함됩니다.
- 누가 누구와 이야기하는지 보여주는 소셜 네트워크
- 서로 관련된 주제를 설명하는 시맨틱 네트워크
- 역할자 간의 연결을 나타내는 충돌 네트워크
- 연결 항공편이 어느 공항에 있는지 나타내는 항공사 네트워크
예시
다음은 링크 분석 사용에 대한 시나리오 예시입니다.
- 범죄 분석가는 범죄 네트워크를 조사하고 있습니다. 휴대폰 기록의 데이터를 사용하여 네트워크 구성원 간의 관계와 계층 구조를 확인할 수 있습니다
- 신용 카드사가 신용 카드 도난을 감지하는 새로운 시스템을 개발하고 있습니다. 이 시스템은 각 고객의 알려진 거래 패턴(예시: 도시, 상점 및 거래 유형)을 사용하여 이상 징후를 식별하고 잠재적 도난 가능성을 고객에게 알려 줍니다.
- 공중 보건 분석가는 북미의 아편 중독 위기를 연구하고 있습니다. 이 분석가는 처방전과 인구 통계 데이터를 사용하여 위기 확산에 따른 새로운 패턴을 식별합니다.
링크 분석 작동 방식
다음 테이블에는 링크 분석의 용어에 대해 간단히 설명되어 있습니다.
| 기간 | 설명 | 예시 |
|---|---|---|
네트워크 | 상호 연결된 일련의 노드 및 링크입니다. | 온라인 소셜 네트워크는 프로필 및 관계 네트워크를 사용하여 사용자를 연결합니다. 항공사 네트워크는 여행객을 출발지에서 목적지로 수송하는 공항 및 항공편 네트워크를 사용합니다. |
노드 | 사람, 장소, 범죄 유형 또는 트윗 등의 객체를 나타내는 포인트 또는 버텍스입니다. 연관된 등록정보가 노드에 포함될 수도 있습니다. | 소셜 네트워크의 프로필 사용자 이름, 고향 또는 고용 기관 등이 연관된 등록정보로 포함될 수 있습니다. 항공사 네트워크의 공항 항공사 이름 등이 연관된 등록정보로 포함될 수 있습니다. |
링크 | 노드 간의 관계 또는 연결입니다. 연관된 등록정보가 링크에 포함될 수도 있습니다. | 네트워크 내 프로필 간의 관계(예시: 친구, 팔로워 또는 연결). 관계의 길이 등이 연관된 등록정보로 포함될 수 있습니다. 항공사 네트워크 내 공항 간의 항공편. 공항 간의 항공편 수 등이 연관된 등록정보로 포함될 수 있습니다. |
중심성
중심성은 네트워크 내 노드에 대한 중요도 측정입니다.
전반적인 중심성은 다음 용도로 사용됩니다.
- 네트워크에서 한 노드가 다른 노드에 미치는 영향을 평가합니다. 예를 들어 뉴스나 일자리 기회를 공유할 때 가장 많은 사용자와 연결된 사용자가 누구인지 분석합니다.
- 다른 노드의 영향을 가장 많이 받는 노드를 식별합니다. 예를 들어 다른 지역의 폭풍으로 인해 항공편을 취소할 때 가장 큰 영향을 받는 공항을 확인합니다.
- 네트워크 전체에 걸쳐 정보, 객체 또는 현상 등의 흐름이나 확산을 관측합니다. 예를 들어 소포가 창고에서 배송지로 어떻게 이동되는지 살펴볼 수 있습니다.
- 네트워크를 통해 현상을 가장 효율적으로 전파하는 노드를 파악합니다. 예를 들어 가장 많은 사람에게 스토리를 전달하려면 어떤 신문사나 채널에 연락해야 하는지 파악합니다.
- 현상의 확산을 차단하거나 방지할 수 있는 노드를 식별합니다. 예를 들어 바이러스 확산을 막기 위한 예방 접종 병원의 위치를 파악합니다.
Insights에서는 연결 중심성, 매개 중심성, 근접 중심성, 고유 벡터 중심성이라는 4가지 방식으로 측정할 수 있습니다.
매개, 근접, 고유 벡터 중심성에 대한 계산은 가중치가 적용되거나 가중치가 적용되지 않을 수 있습니다.
연결 중심성
연결 중심성은 노드의 직접 연결 수를 기반으로 측정합니다. 가장 직접적인 영향을 미치는 노드를 확인하려는 경우 연결 중심성을 사용합니다. 예를 들어 소셜 네트워크에서 연결이 많은 사용자일수록 연결 중심성이 높습니다.
다음 방정식을 사용하여 노드 x의 연결 중심성을 계산할 수 있습니다.
degCentrality(x)=deg(x)/(NodesTotal-1)여기서 각 항목 정보는 다음과 같습니다.
- NodesTotal = 네트워크의 노드 수
- deg(x) = 노드 x에 연결된 노드 수
링크가 방향성인 경우(즉, 노드 간의 정보가 한 방향으로만 흐르는 경우) 연결 중심성은 진입 차수 또는 진출 차수로 측정할 수 있습니다 소셜 네트워크의 경우 진입 차수는 사용자가 팔로우하는 프로필의 수를 기반으로 하며 진출 차수는 사용자의 팔로워 수를 기반으로 합니다.
진입 차수 연결성은 다음 방정식을 통해 계산됩니다.
indegCentrality(x)=indeg(x)/(NodesTotal-1)여기서 각 항목 정보는 다음과 같습니다.
- NodesTotal = 네트워크의 노드 수
- indeg(x)=노드 x쪽으로 흐르도록 연결된 노드 수
진출 차수 연결성은 다음 방정식을 통해 계산됩니다.
outdegCentrality(x)=outdeg(x)/(NodesTotal-1)여기서 각 항목 정보는 다음과 같습니다.
- NodesTotal = 네트워크의 노드 수
- outdeg(x) = 노드 x에서 바깥쪽으로 흐르도록 연결된 노드 수
방향성 그래프의 경우 Insights는 기본 설정에 따라 진출 차수 연결성을 기준으로 노드 크기를 정합니다.
매개 중심성
매개 중심성은 노드가 다른 노드 간의 최단 경로에 속하는 범위를 기반으로 합니다. 다른 노드를 서로 연결하는 데 사용되는 노드를 확인하려는 경우 매개 중심성을 사용합니다. 예를 들어 여러 친구 그룹에 연결된 소셜 네트워크 사용자는 한 그룹에만 연결된 사용자보다 매개 중심성이 더 큽니다.
다음 방정식을 사용하여 노드 x의 매개 중심성을 계산할 수 있습니다.
btwCentrality(x)=Σa,bϵNodes(pathsa,b(x)/pathsa,b)여기서 각 항목 정보는 다음과 같습니다.
- Nodes = 네트워크의 모든 노드 수
- pathsa,b = 모든 노드 a와 b 간의 최단 경로 수
- pathsa,b(x) = 노드 x를 통해 연결되는 노드 a와 b 간의 최단 경로 수
위의 매개 중심성 방정식에는 네트워크 크기가 고려되지 않으므로 대형 네트워크의 매개 중심성 값이 소형 네트워크보다 큰 경향이 있습니다. 크기가 다양한 네트워크 간에 비교하려면 차트의 노드 쌍 수로 나누어 매개 중심성 방정식을 정규화해야 합니다.
비방향성 차트를 정규화하려면 다음 방정식을 사용합니다.
1/2(NodesTotal-1)(NodesTotal-2)여기서 각 항목 정보는 다음과 같습니다.
- NodesTotal = 네트워크의 노드 수
방향성 차트를 정규화하려면 다음 방정식을 사용합니다.
(NodesTotal-1)(NodesTotal-2)여기서 각 항목 정보는 다음과 같습니다.
- NodesTotal = 네트워크의 노드 수
근접 중심성
근접 중심성은 노드 간 최단 네트워크 경로 거리의 평균을 기반으로 합니다. 네트워크의 다른 노드와 가장 가까이 연결된 노드를 확인하려는 경우 근접 중심성을 사용합니다. 예를 들어 소셜 네트워크의 연결이 많은 사용자일수록 다른 사람을 통해 연결된 사용자(즉, 친구의 친구)보다 근접 중심성이 큽니다.
비고:
노드 간의 거리는 지리적 거리가 아닌 해당 노드를 분리하는 링크 수를 나타냅니다.
다음 방정식을 사용하여 노드 x의 근접 중심성을 계산할 수 있습니다.
closeCentrality(x)=(nodes(x,y)/(NodesTotal-1))*(nodes(x,y)/dist(x,y)Total)여기서 각 항목 정보는 다음과 같습니다.
- NodesTotal = 네트워크의 노드 수
- nodes(x,y) = 노드 x에 연결된 노드 수
- dist(x,y)Total = 노드 x에서 다른 노드에 이르는 최단 경로 거리의 합
고유 벡터 중심성
고유 벡터 중심성은 중요한 다른 노드에 연결되고 있는 중요한 노드를 기반으로 합니다. 영향을 미치는 클러스터의 일부인 노드를 확인하려는 경우 고유 벡터 중심성을 사용합니다. 예를 들어, 소셜 네트워크에서 연결이 많은 다른 사용자와의 연결이 많은 사용자는 연결이 적거나 연결이 적은 다른 사용자와 연결된 사용자보다 고유 벡터 중심성이 높습니다.
노드 x의 고유 벡터 중심성은 다음 등식을 사용하여 가장 큰 고유 벡터를 찾을 수 있는 지수 반복을 사용하여 계산됩니다.
Ax=λx여기서 각 항목 정보는 다음과 같습니다.
- λ = 고유 값
- x = 고유 벡터
- A = 선형 변환을 설명하는 행렬
엣지 가중치
근접, 매개, 고유 벡터 중심성에 대한 계산은 가중치가 적용되거나 가중치가 적용되지 않을 수 있습니다. 가중치가 적용되지 않은 중심성 계산은 값이 1인 균일한 가중치로 엣지를 설정하며, 가중치가 적용된 계산은 필드 값을 사용하여 각 엣지에 값을 할당합니다.
비고:
정의되지 않은 가중치에는 값 1이 할당됩니다. 엣지 가중치에는 Null 또는 누락된 값이 없는 필드를 할당하는 것이 좋습니다.
고유 벡터 중심성의 경우 가중치는 노드 간의 연결 강도를 결정하는 데 사용됩니다. 고유 벡터 중심성은 네트워크 내 노드의 중요도를 측정하기 때문에 가중치 값이 높을수록 연결 노드의 값이 높아집니다.
근접 및 매개 중심성의 경우 가중치 값은 노드 간의 거리를 나타냅니다. 엣지 가중치가 높을수록 노드 간의 거리가 더 크다는 것을 의미하며, 이로 인해 최단 경로에서 엣지가 사용될 가능성이 줄어듭니다. 원하는 가중치 필드의 숫자가 높을수록 중요도가 높아짐을 나타내는 경우(예시: 소셜 네트워크의 구성원 간에 전송된 메시지 수는 연결된 구성원 수를 나타냄) 새 필드는 역값으로 계산되어야 합니다. 역값 필드를 계산하려면 다음 방정식을 사용합니다.
weight=ABS(field-MAX(field))+IF(MIN(field)<0, ABS(MIN(field)), MIN(field))가중치가 적용되지 않은 근접 또는 매개 계산의 경우 최단 경로는 가장 적은 수의 링크를 사용하는 경로입니다. 아래 예시에서는 4개의 노드(A, B, C, D) 및 가중치가 균일한 네트워크를 보여줍니다. 노드 A를 노드 D에 연결하는 A-B-D 또는 A-B-C-D의 두 경로가 있습니다. A-B-D는 링크 수가 적으므로 최단 경로입니다.

가중치 계산은 필드 값을 기반으로 각 엣지에 가중치를 적용합니다. 가중치 근접 및 매개 중심성은 Bellman-Ford 알고리즘을 사용하여 노드 간의 최단 경로를 찾습니다.
아래 예시에서는 4개의 노드 및 가중치가 적용된 엣지가 있는 네트워크를 보여줍니다. A-B-D 경로의 값은 15이고 A-B-C-D 경로의 값은 9입니다. A-B-C-D의 엣지 값이 가장 낮으므로 최단 경로입니다.

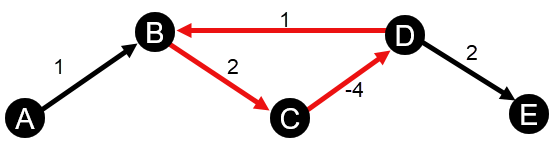
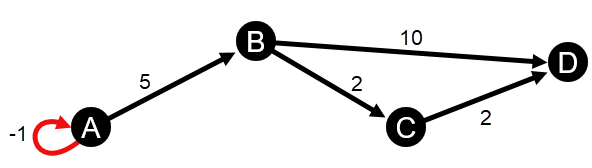
가중치가 적용된 근접 및 매개 중심성 계산은 음수의 가중치 주기를 지원하지 않습니다. 음수 가중치 주기가 감지된 경우 모든 중심성 값은 0으로 설정됩니다. 음수 가중치 주기는 다음과 같은 경우에 발생할 수 있습니다.
- 이 그래프에는 음수 주기가 포함되어 있습니다.
- 이 그래프에는 음수 자체 반복이 포함되어 있습니다.
- 이 그래프에는 방향이 지정되지 않은 음수 엣지가 포함되어 있습니다.

리소스
다음 리소스를 사용하여 링크 분석에 대해 자세히 알아봅니다.