一連のポイントまたはエリアのトレンドを計測する一般的な方法は、X,Y,Z の各ディメンションで個別に標準距離を計算することです。 これらの計測により、フィーチャの分布を囲む楕円 (または楕円体) の軸が定義されます。 この方法では、平均中心からの X 座標と Y 座標の標準偏差が算出されて、楕円の軸が定義されるため、この楕円は「標準偏差楕円」と呼ばれます。 3D では、平均中心からの Z 座標の標準偏差も計算され、結果は「標準偏差楕円体」と呼ばれます。 この楕円または楕円体により、フィーチャの分布が引き延ばされて、特定の向きを示しているかどうかを確認できます。
マップにフィーチャを描画することでおおよその向きを把握することもできますが、標準偏差楕円を使用すると、トレンドが明確に示されます。 標準偏差楕円は、フィーチャのロケーション、またはフィーチャに関連付けられている属性の影響を受けるロケーションのどちらかを使用して算出できます。 後者は、「加重標準偏差楕円」と呼ばれます。
演算
標準偏差楕円は、次の式で計算されます。
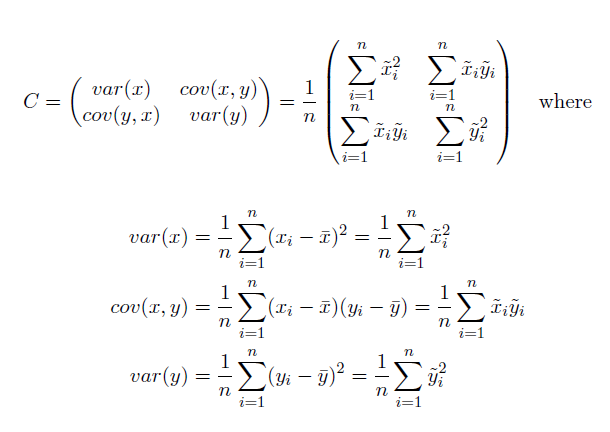
x と y がフィーチャ i の座標の場合、{x̄, ȳ} はフィーチャの平均中心を表し、n はフィーチャの合計数と等しくなります。
サンプルの共分散行列を正規化すると、固有値と固有ベクトルで表現される行列になります。 X 軸と Y 軸の標準偏差は、次のようになります。
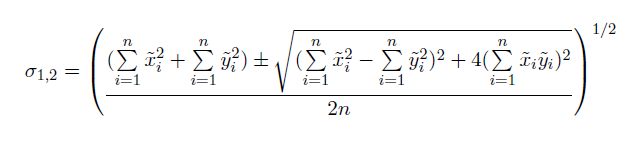
これらの方程式は、3 次元データのソリューションにも拡張できます。
出力と解釈
標準偏差は、データの分散や拡散を理解するのに役立ちます。 1 次元の正規分布データを操作する場合、68%、95%、99.7% のデータ値がそれぞれ 1、2、3 標準偏差内に存在します。 ただし、これにより次元が高い空間データ (X、Y、Z 変数) を操作する場合、これらの割合は正しくありません。 たとえば、2 次元の正規分布データの場合、1 標準偏差楕円ポリゴンでフィーチャの約 63 パーセントがカバーされ、2 標準偏差でフィーチャの約 98 パーセントがカバーされ、3 標準偏差でクラスター内のフィーチャの約 99.9 パーセントがカバーされます。 同様に、3 次元の場合は、パーセンテージは 61、99、100 になります。
そのため、標準偏差は調整係数によってスケール処理され、2D データおよび 3D データのフィーチャの 68%、95%、99% を含む楕円または楕円体が生成されます (データが空間的正規分布に従うと仮定した場合)。 以下の表に、分散の調整係数 (標準偏差の二乗) を示します。
| 1 次元データ | 2 次元データ | 3 次元データ | |
|---|---|---|---|
1 標準偏差 | 1.00 | 1.41 | 1.73 |
2 標準偏差 | 2.00 | 2.83 | 3.46 |
3 標準偏差 | 3.00 | 4.24 | 5.20 |
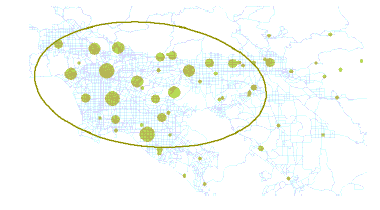
2 次元データの場合、[分布指向性分析 (Directional Distribution (Standard Deviational Ellipse))] ツールは、すべてのフィーチャ ([ケース フィールド] パラメーターの値が指定されている場合はすべてのケース) の平均中心を中心とする楕円ポリゴンが含まれる新しいフィーチャクラスを作成します。 これらの出力楕円ポリゴンの属性値には、2 つの標準距離 (長軸と短軸)、楕円の向き、およびケース フィールド (指定されている場合) が含まれます。 楕円の向きは、時計回りに正午の位置から計測される長軸の回転を表します。 また、表示する標準偏差の数 (1、2、または 3) を指定し、フィーチャの異なるパーセンテージをカバーすることもできます。
3 次元ポイント データ (Z 対応で高度のような 3D 属性情報を含むデータ) の場合、このツールは、すべてのフィーチャ (ケース フィールドを使用する場合はすべてのケース) の平均中心を中心とする楕円体マルチパッチが含まれる新しいフィーチャクラスを作成します。 これらの出力楕円体の属性値には、3 つの標準距離 (長軸、短軸、高さ軸)、楕円体の角度、傾き、ロールに関する情報、およびケース フィールド (指定されている場合) が含まれます。 楕円体の角度、傾斜、ロールの値は、3D 空間における楕円体の方向を記述します。 また、表示する標準偏差の数 (1、2、または 3) を指定し、フィーチャの異なるパーセンテージをカバーすることもできます。
適用例
- 一連の犯罪の分布トレンドをマッピングすることにより、特定の物理フィーチャ (飲食店街や特定の大通りなど) とのリレーションシップを把握することができます。
- 特定の汚染物質の地下水井戸サンプルをマッピングすることにより、毒素がどのように拡散しているかを把握し、これに基づいて抑止作戦を展開することができます。
- さまざまな人種または民族グループの楕円のサイズ、形状、および重なりを比較することにより、人種的または民族的な分離を把握することができます。
- 感染症の発生を示す楕円を時系列的にプロットすることで、その拡散をモデリングすることができます。
- 特定のカテゴリの暴風について高度の分布を調べることは、大気の状態と航空機事故の関係を調査する際に役立つ検討要素です。
参考資料
Chew, Victor 『Confidence, prediction, and tolerance regions for the multivariate normal distribution』 Journal of the American Statistical Association. 61.315 (1966): 605-617. https://doi.org/10.1080/01621459.1966.10480892.
Fisher, N. I., T. Lewis, and B. J. J. Embleton. 1987. 『Statistical Analysis of Spherical Data』 First edition. Cambridge: Cambridge University Press. Cambridge Books Online. Web. 26 April 2016. https://doi.org/10.1017/CBO9780511623059.
Levine, Ned 『CrimeStat III: a spatial statistics program for the analysis of crime incident locations (version 3.0)』 Houston (TX): Ned Levine & Associates/Washington, DC: National Institute of Justice (2004). https://doi.org/10.3886/ICPSR02824.v1.
Wang, Bin, Wenzhong Shi, and Zelang Miao. 2015. 『Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space』 PLoS ONE. 10(3), e0118537.https://doi.org/10.1371/journal.pone.0118537.