直線距離を計算し、バリアまたはサーフェス ラスターを考慮して計算をできる限り調整し、その距離に達する速度を決定します。 コスト サーフェスは、その距離に達する速度に影響を与える 4 つのファクターの 1 つです。 他の 3 つは、ソース特性、垂直方向ファクター、および水平方向ファクターです。
コスト サーフェスは、地表を移動するときに移動者が遭遇するものを取り込みます。 野原を横切るのは、森を通り抜けるよりも簡単です。森を通り抜けるのは、湿地を通り抜けるよりも簡単です。 コスト サーフェスの各値に調整された直線距離を掛けて、移動者が特定距離に到達する速度を特定します。
コスト サーフェスの結果として、移動者は、森や湿地に比べて野原においてより速い速度で、調整された直線距離単位を進むことができます。
直線距離は、距離単位 (メートルやフィートなど) で表されます。 特定距離に到達する速度を特定する際、単位は、ドル、好適度、消費エネルギー、リスクなどです。 速度は、距離計測の単位ごとのコストです。

コスト サーフェスを作成する作業は、複数の手順で構成されます。 初めに、移動に影響する条件を特定します。 次に、条件値を共通のコスト スケールに変換します。 最後に、条件に重みを付けて結合します。
このタイプの解析は、最小コスト解析として知られています。 コスト サーフェスは、インピーダンスまたは摩擦サーフェスとも呼ばれます。 コストが高い場所で調整された直線距離単位を進むことは、より労力や費用がかかる、あるいはより速度が落ちます。 コスト サーフェスの作成は、適合性サーフェスの作成と似ていますが、適合性サーフェスでは、より高い値が推奨されます。 コスト サーフェスでは、値が低いほど移動が簡単になります。
コスト サーフェスを作成するには、さまざまなファクターを結合できます。 たとえば、動物の移動についてコスト サーフェスを作成する場合、土地利用タイプ、道路からの距離、水域からの距離などのファクターを使用して、動物が地表を移動する際の適合度を取り込むことができます。 条件の値はさまざまな意味を持つので、各条件は、結合前に同一のコスト スケールに変換する必要があります。
多くの場合、コスト サーフェスは、コスト距離解析のコスト単位を定義します。 ソース特性、垂直方向ファクター、および水平方向ファクターは、それらの単位の乗数です。 各乗数は、コスト サーフェスで定義された同一コスト単位で相対化されている必要があります。 4 つの速度制御ファクター (コスト サーフェス、ソース特性、垂直方向ファクター、および水平方向ファクター) のうち複数が指定されている場合、それらの 1 つだけが単位を持つことができ、他の係数は、それらの単位を変更する単位のない乗数です。
コスト サーフェスにより、実際の地表での移動者の動きをシミュレートすることができます。
コスト サーフェスの使用例
コスト サーフェスは、次のようなさまざまなシナリオの解決に使用できます。
- 建設予定の学校への道路を建設するためにコストが一番低いルートを特定します。 コスト サーフェスの単位は、建設にかかる 1 メートルあたりのドルです。
- 野生生物の生息地域間をコリドーで繋ぎ、種が地域間を移動できるようにします。 コスト サーフェスの単位は、各場所のフィーチャを通過するときの 1 フィートあたりの好適度です。
- 油田を精製所と接続する新しいパイプラインを特定します。 コスト サーフェスの単位は、パイプラインが各場所に与える環境への影響に基づきます。
- 遠方の地域で怪我をしたハイカーに最短で到達する道を決定します。 コスト サーフェスの単位は、1 メートルあたりの分です。
コスト サーフェスの組み込み
距離の解析は、概念的に、次の関連機能領域に分けることができます。
- 直線距離を計算し、必要に応じて、バリアまたはサーフェス ラスターを使用して計算を調整します。
- 直線距離が計算されたら、必要に応じて、コスト サーフェス、ソース特性、垂直方向ファクター、および水平方向ファクターにより、その距離に達する速度を決定します。 累積距離ラスターを作成します。
- 最適ネットワーク、特定のパス、またはコリドーを使用し、生成される累積距離サーフェス上に領域を接続します。
2 つ目の機能エリアから、下図のように、コスト サーフェスによってその距離に達する速度を決定します。 シナリオには、4 つの森林管理事務所のコレクション (紫のドット) と数本の河川 (青いライン) が含まれています。
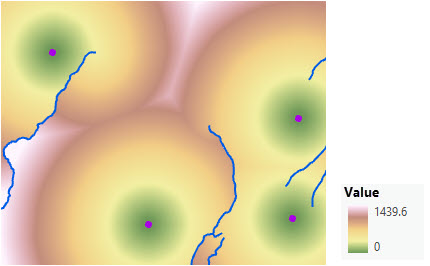
コスト サーフェスを追加して、地表を移動する移動者をシミュレートします。 以下の図で、距離が各管理事務所から均等に伸びていないことに注意してください。
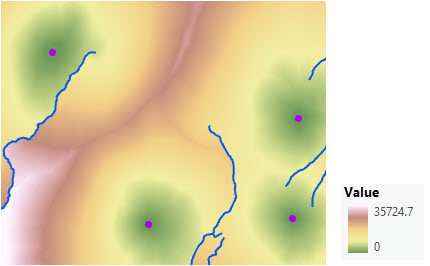
直線距離の速度を表すコスト サーフェス
調整された直線距離に達する速度を特定するためのコスト サーフェスを作成するには、以下の手順を行います。
- 初めに、移動に影響するファクターを定義する条件を特定します。 これらの条件は、移動者が地表を移動してその距離にどのように到達するかを取り込みます。
- 土地利用などの一部のデータは、条件として直接使用できます。 傾斜方向、フィーチャからの距離、可視性などのその他の条件は、ベース データから生成される必要があります。 これらの条件を生成するために使用できるツールには、[距離累積 (Distance Accumulation)]、[傾斜方向 (Aspect)]、[測地線可視領域 (Geodesic Viewshed)]、[カーネル密度 (Kernel Density)]、および [サーフェス パラメーター (Surface Parameters)] があります。
- 条件を共通のスケールに変換します。 変換は、[再分類 (Reclassify)] および [関数によるリスケール (Rescale by Function)] ツールで行うことができます。
- 変換した条件に重みを付けて結合します。 [加重合計 (Weighted Sum)] ツールを使用して行います。
コスト サーフェスは、距離に達する速度に影響します
コスト サーフェスは、コスト、摩擦、移動に対する各場所の好適度を、その場所の特性に基づいて特定します。 適用方法やモデル化されているコスト単位に関係なく、一般的なワークフローは似ています。
建設、時間、エネルギーのコストなど、絶対コストは究極のコストですが、各場所に定義するのが難しい場合があります。 ただし、多くの用途で、単一の絶対コスト単位は存在しません。 たとえば、2 か所をつなぐハイキング トレイルやサイクル トレイルを特定するためのコスト サーフェスを作成している場合、コスト単位にエネルギーや時間を単独で使用しても、トレイルの行き先に影響を与えるその他のファクターは取り込まれません。 それらのファクターには、きれいな景色、土地所有権、環境保護指定区域外などがあります。 野生生物用のコリドーを設けるためのコスト サーフェスを作成すると、動物は、適切な生息地内の移動と安全のバランスを取ることができます。 いずれの場合も、移動を決定した範囲を取り込める単一のコスト単位がありません。
その場合は、好適度、安全、リスクなどの相対的に主観的なコスト単位が使用されます。 各条件値は、割り当てられたコストが主観的コストに基づいて相互に相対化された共通のコスト スケールに割り当てられます。 つまり、コスト 10 は、コスト 5 より移動が 2 倍難しいということです。 各条件の各値は、同じ共通のコスト スケールに変換されます。
コスト サーフェスがコスト解析の単位を定義している場合、他の速度制御ファクター (ソース特性、垂直方向ファクター、および水平方向ファクター) は、指定されたコスト単位を変更する、単位のない乗数です。
絶対コスト単位は、いくつもの Spatial Analyst ツールを使用して直接割り当てることができます。 コスト サーフェスを作成するために主観的なコスト単位を定義する場合は、通常以下に説明するワークフローが使用されます。
コスト サーフェス ワークフロー
相対コストを指定する場合のコスト サーフェス作成ワークフローは次のとおりです。
- 移動のコストに影響する条件を特定し、ベース データを集めます。
- 必要に応じて、ベース データから条件を生成します。
- 各条件の値を共通のコスト スケールに変換します。
- 条件を相互に相対的に重み付けし、それらの条件を組み合わせてコスト サーフェスを作成します。
コスト サーフェスが作成されると、コスト サーフェス上の最小コスト パスで領域を接続することができます。
前述のように、コスト サーフェスの作成は、適合性サーフェスの作成と同様の手順で行います。 共通の手順は、条件の特定、ベース データの収集、ベース データからの必要な条件の生成、条件値の共通スケールへの変換、条件の重み付け、および条件の結合です。 より高い値が推奨される最終的な適合性サーフェスとは異なり、コスト サーフェスは、より低いコストを表すので、移動に対してより低い値が推奨されます。 コスト サーフェスは、最小コスト解析で使用されます。 結果として、変換を実行すると、移動により適した場所ほどより低い値が割り当てられます。
以下のセクションでは、このワークフローの適用例について説明します。 目標は、ボブキャットが生息地域間を移動するための、野生生物用のコリドーを特定することです。 ワークフローは、例示するためのものであり、ボブキャットへのすべての相互関係を実際に定義するものではありません。 前述のワークフローを応用して、他の多数の用途のコスト サーフェスを作成することができます。
目的とコスト単位の定義
初めに、移動の目的を定義します。 目的は、解決する問題によって異なります。 たとえば、電柱を設置するために使用されるコスト サーフェスの目的は、設置費用を最小限にすることが考えられます。 2 か所の火災現場で消防士がリソースを移動するルートを特定する場合、目的は、できる限り迅速な現場間の移動が考えられます。 ボブキャットのシナリオでは、コスト サーフェスの目的は、ボブキャットが生息地間を安全に移動でき、同時に特定リソースへのアクセスを維持することです。
次に、コスト単位を決定します。 電線を設置する場合は、各条件を建設コストに基づいて変換できます。 消火活動のためのルートを特定する場合、コスト単位として時間が考えられます。 ボブキャットのためのコリドーでは、単位の定義は 2 つの課題を示します。 1 つは、客観的な測定可能なコスト単位がないことです。 もう 1 つは、条件にさまざまな目的があるということです。 たとえば、河川への距離の条件は水の必要性であり、道路からの距離は安全確保です。 この場合は、条件を、結合前に相対的に主観的な好適度コスト スケールで変換する必要があります。
目的と単位が定義されたら、モデルの結果を評価する方法を決定します。 ボブキャットのコスト サーフェスでは、結果のパスが最適かどうかを見極めるため、コリドーでボブキャットがそのパスを使って生息地域間を移動しているかどうかを確認します。
次の画像は、ボブキャットのコスト サーフェスの作成を示しています。
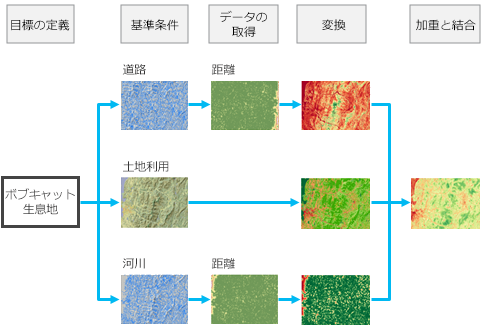
移動のコストに影響する条件を特定します
これで、目的、単位、解析のための評価方法が定義されました。コスト サーフェス作成の最初の手順は、移動を定義する条件の特定です。 このサンプル ケースでは、ボブキャットが地表を移動するときに優先するものです。 各条件は、モデルの全体的な目標 (ボブキャットが、重要なリソースにアクセスできつつ、生息地域間を安全に移動できること) を達成するために必要なものです。 特定された条件には、ボブキャットの移動のニーズに応じた相互関係が取り入れられている必要があります。
簡素化したボブキャットの例では、次の条件が考慮に入れられます。
- 土地利用タイプ - ボブキャットは、身を隠すため森林の中を移動することを好み、開発地域や開発途中の場所は移動しません。
- 道路までの距離 - 安全のため、ボブキャットは道路から離れた場所を移動することを好みます。
- 河川からの距離 - ボブキャットは、水が必要なため、地表を移動しつつ水源に近い場所にとどまろうとします。
必要に応じて、ベース データから条件を生成します
ボブキャットの例の土地利用タイプのように、コスト サーフェスの作成に直接使用できる条件もあります。 ボブキャットは、さまざまな土地利用タイプの影響を直接受けます。 その他の条件を生成する必要があります。 道路や河川自体は条件ではありません。ボブキャットに影響を与えるのは、道路や河川からの距離であることに注意してください。
道路および河川への距離のデータセットは最初から提供されているわけではないので、適切なツールを使用して、ベース データを基にこれらの条件を作成することができます。 道路の条件について、それぞれの場所の最寄りの道路からの距離を特定するには、[距離累積 (Distance Accumulation)] ツールを使用します。またこのツールで、河川の条件について、河川からの距離も特定します。
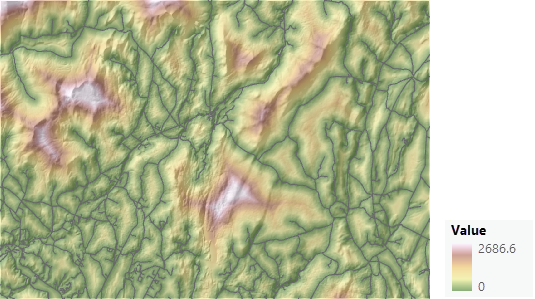
各条件の値を共通のコスト スケールに変換します。
数学的に、土地利用、道路への距離、河川からの距離のラスターを足し算するだけでは、意味のある値を得ることはできません。 たとえば、ある場所の土地利用の値が 4 (単身向け住宅) であるとします。 また、道路からの距離は 627 メートル、河川からの距離は 2,252 メートルあります。 これらの値を加算すると 2,883 ですが、これは意味がありません。 条件ラスターを加算する前に、各条件の値を共通のコスト設定スケールに変換する必要があります。
この例では、1 から 10 の共通コスト スケールが使用されます。 条件の各値に対し、最も簡単に移動できるあるいは最も好適な特性を含む場所のコスト値は低くなり、より困難または不適切な場所のコスト値は高くなります。 たとえば、道路から 100 メートル以内の場所は好適度が最低であり、コスト値は 10 が割り当てられます。100 ~ 300 メートルの距離ではコスト値は 5、300 メートルを超える距離では、ボブキャットが道路から離れて移動するのを好むためコスト値 1 が割り当てられます。
各条件の値を 1 ~ 10 のコスト スケールに変換する際、スケール内で相対的に値を変換します。 つまり、コスト値 3 が割り当てられた場所は、コスト値 6 が割り当てられた場所の 2 倍の好適度であり、コスト値 10 は、コスト値 1 が割り当てられた場所より移動が 10 倍難しいと解釈されます。
この変換処理は、コスト サーフェスで特定された各条件の各値に対して適用されます。 ボブキャット モデルの土地利用条件の場合、森林など好適な土地利用タイプにはコスト値 1 (移動に好適で低コスト)、住宅地には 5、工業地域には 9 が割り当てられます。 道路からの距離の条件の場合、道路に近い場所はより高いコスト値 9 および 10 が割り当てられ、道路から離れた場所は (ボブキャットが移動を好む場所なので) より低いコスト値が割り当てられます。 河川までの距離の条件では、河川に近い場所ほど好適なので、近い場所はコスト値 1 や 2、離れた場所はより高い値 9 や 10 が割り当てられます。
割り当てられたコストには、条件間で同じ好適度を持つことが望まれます。 つまり、コスト値 5 が割り当てられた変換済みの道路からの距離は、同じくコスト値 5 が割り当てられた土地利用タイプや河川への距離と同じ好適度である必要があります。
条件を変換する場合は通常、[再分類 (Reclassify)] および [関数によるリスケール (Rescale by Function)] ツールが使用されます。 各条件について、これらのツールには同じコスト スケールが指定されます。 この例では、1 から 10 のコスト設定スケールが使用されます。
土地利用タイプはカテゴリ データです。土地利用タイプをコストにマッピングするには、1 対 1 変換が使用されます。 [再分類 (Reclassify)] ツールが使用されます。 再分類テーブルで、森林には 1、工業地域には 9、というように値が割り当てられます。
| 値 | 新規 |
|---|---|
農業 | 2 |
裸地 | 1 |
造成済み、高強度 | 9 |
造成済み、低強度 | 5 |
造成済み、中強度 | 8 |
森林、針葉樹 | 1 |
森林、落葉樹 | 2 |
森林、落葉樹 - 針葉樹の混合 | 2 |
草地 | 4 |
灌木/低木 | 3 |
水域 | 10 |
湿地帯 | 9 |
NODATA | NODATA |
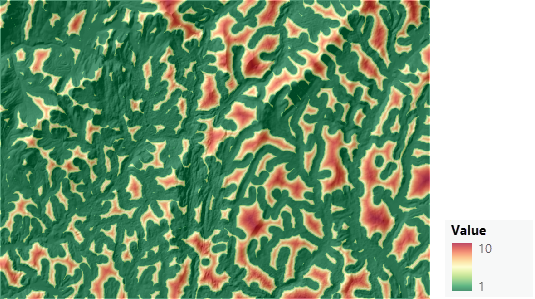
以下は、生成された変換後の土地利用マップです。 緑色の場所は移動により好適であり、赤い場所は移動により不適切です。

道路からの距離および河川からの距離は連続データです。 条件の値を変換してコストの相互作用を取り込むため、関数が使用されます。 ボブキャットが道路から 1 歩ずつ移動すると、指定した関数に基づいて、好適度またはコストが連続的に小さくなります。
[関数によるリスケール (Rescale by Function)] ツールの中心機能は、好適性が高い属性ほど高い値が割り当てられる適合性モデルに適しています。 最小コスト解析では逆のロジックになります。 移動により好適なエリアは、コストがより少ないことを示す低い値が割り当てられます。 [関数によるリスケール (Rescale by Function)] ツールは、次の 2 つの方法のいずれかで、この逆のロジックに適応することができます。
- ツールで、適合性関数の逆関数を選択します。 つまり、適合性モデルでは、河川への距離の条件に Small 関数を適用でき、河川に近いほど適合性が高く、より高い値が割り当てられることを示します。 コスト サーフェスで河川からの距離が使用されている場合は、Large 関数が使用され、遠い場所ほど高い (好適度が低い) 値が割り当てられることを示します。 近い場所ほど低い値 (低コスト) が割り当てられ、移動により好適です。
- 適合性モデルで使用される同じロジックを、逆にして適用できます。 Small 関数は、適合性モデルの河川からの距離の条件に対して、およびコスト サーフェスの河川からの距離の条件を変換する場合に指定できます。 ただし、コスト サーフェスの場合、[From scale] および [To scale] パラメーターは、1 ~ 10 から 10 ~ 1 に入れ替える必要があります。 その結果、より近い場所に [To scale] の値が割り当てられ、移動のコストが最小なので 1 が割り当てられるようになります。

ボブキャットが河川の近くを移動したいという好適度を取り込むため、河川からの距離の条件には別の関数が割り当てられました。
条件値をコストに変換する際に、建設コストや時間コストなどの絶対コスト単位を使用している場合、直接割り当てや数式を使用することができます。 これらの式は、前述の相対変換の手順ではなく、[ラスター演算 (Raster Calculator)] を使用して実行することができます。
ヒント:
コストの値は常に正です。入力コスト ラスターは 0 以下のセル値を持つことができません。 0 以下の値がある場合は、範囲全体をリスケールして 0 より大きくするか、問題の値を小さい正の値に置き換えます。 そのためには [Con] ツールを使用します。 値 0 のエリアが解析から除外するエリアを表している場合は、[距離累積 (Distance Accumulation)] を実行する前に、それらの値を NoData に変更します。 そのためには、[Set Null] ツールを使用します。
これで各条件の値が、共通のコスト スケールに対して相互に相対的に変換され、変換された条件を結合することができます。
条件を相互に相対的に重み付けし、それらの条件を組み合わせてコスト サーフェスを作成します
変換した 3 つの条件を足し算すると、その和は 3 ~ 30 の間になります。 値が 3 の場所が、移動に最も好適な場所です。 これは、森の中で、道路から離れ、河川に近い場所です。 値が高い場所は、その特性に基づいて好適ではない (移動のコストが高い) と解釈されます。
ただし、ボブキャットの移動コストにとって、他の条件よりも重要で影響がより大きいものがあるかもしれないので、足し算する場合に考慮します。 その場合は、その条件に対しては他の条件よりも重みを付けます。 はっきりと区別するために、変換処理で、条件の値を相互に相対的に重み付けしています。 重み付けは、各条件の相対的な重要性を定めます。
重みは、条件の各変換後の値に適用される乗数です。
ボブキャットの適合性モデルでは、条件への加重が大きいほど、その条件がボブキャットの生態にとってより重要であることを示します。 ただし、コスト サーフェスでは、加重は、この条件が他の条件よりも移動にとって重要またはコストがかかることを示します。
ボブキャットのコスト サーフェスでは、ボブキャットは、安全のため道路付近の移動を避けたがると判断されます。 その結果、変換後の道路からの距離は、河川からの距離の条件よりも、割り当てられる重みが大きくなります。 たとえば、ある場所が当初、道路から近いために、道路からの距離についてコスト 10 を割り当てられたとします。 その場所は、河川にも近いので、河川への距離についてコスト 1 が割り当てられます。 道路からの距離の条件に重み 1.5 が割り当てられ、河川からの距離の条件に重み 1 が割り当てられた場合、その場所は、生成されたコスト サーフェスで、合計 16 (10 x 1.5 + 1 の計算結果) のコスト値が割り当てられます。 その結果、道路に近い場所はコストが高くなり、移動には適していないことになります。
この例では、土地利用の条件にも重み 1 が割り当てられます。

重み付けのため、最小コスト解析は加重最小コスト解析とも呼ばれる場合があります。
注意:
ドルや時間などの測定可能な絶対コスト単位が使用される場合は、重み付けをしないでください。 条件が重要であるかどうかに関係なく、絶対コストは変化しません。 ドルのコストや時間は実際のコストです。 重み付けされると、絶対単位は無効になり、そのコストは相対スケールになります。
これでコスト サーフェスが作成されました。 コスト サーフェスは、各場所の特性に基づき、ボブキャットの立場から、移動について各場所の好適性を相互に相対的に示します。 ボブキャット モデルの最終目的は、生成された累積コスト ラスター上で、ボブキャットの一連の生息地域を野生生物用のコリドーで繋ぎ、ボブキャットが繋がった地域を移動できるようになることです。
生息地域は、以下の方法で繋ぐことができます。
- 最小コスト ネットワークを作成します(「領域と最適なネットワークとの接続」をご参照ください)。
- 特定の生息地域を相互に繋ぎつなぎます(「最適パスを使用した位置の接続」をご参照ください)。
- コリドーにより生息地域を繋ぎます (「コリドーによる位置の接続」をご参照ください)。
傾斜角とコスト サーフェス
コスト サーフェスは、調整された直線距離に達する速度を制御できる 4 つのファクターの 1 つです。 コスト サーフェスでは、セルを東から西へ、西から東へ、北から南へ、あるいは南から北へ移動しても、どの対角線方向に移動しても、コストは同じです。 ただし、そのセルを通ってどの方向に進むかは、移動者にとっては、場合によっては重要です。 坂を上る場合と坂を下る場合では、異なる労力が必要です。 その傾斜をどのように進むかが重要な場合もあります。 たとえば、急斜面を、傾斜に対して直角に移動する (等高線に沿って移動する) と、急斜面を直接上るより労力は少なくなります。
[傾斜角 (Slope)] ツールは、処理するセルの中心の高さから 8 つの近傍セルの各中心の高さまでの垂直方向の長さを水平方向の長さで除算した値を特定することで、傾斜角を計算します。 8 つの傾斜角で最大の傾斜角がそのセルに割り当てられます。 セルには最大降下が割り当てられるので、そのセルへの移動の方向性は取り込まれません。 移動をモデリングする際、ある場所の勾配がどの程度急であるかではなく、その傾斜をどのように進むかが重要な場合があります。 コスト サーフェスで傾斜角ラスターが使用されていると、移動者は傾斜角が急なセルを不必要に避ける可能性があります。
一般に、移動者が斜面を進む方向が重要な場合、コスト サーフェスではなく、垂直方向ファクターによってその方向が取り込まれる必要があります。 多くの場合、傾斜角はコスト サーフェスの入力として誤って使用されます。
ただし、傾斜角ラスターがコスト サーフェスへの適切な入力となる場合があります。 たとえば、新しいハイキング トレイルを探しており、あるセルの傾斜角が非常に急である場合、移動者がそのセルに入る方向に関係なく、移動速度は遅くなります。 この例では、傾斜角の方向性は重要ではないので、コスト サーフェスに傾斜角ラスターを含めることが適切です。

移動者にとって、問題は、斜面の勾配の程度ではなく、その斜面をどのように進むかです。 急斜面を上るには最大限の労力が、下るには最小限の労力が必要です。斜面に沿って移動する場合はその中間程度の労力が必要です。 傾斜がある土地被覆も移動に影響します。 舗装されていない自然の地面の移動は、道路の移動よりも大変です。 ハイカーのシンボルは、移動する斜面や土地被覆をどの程度簡単に克服できるかに基づいて、色分けされます。 緑色のシンボルは、赤いシンボルより速く移動できます。
速度制御ファクターの単位
調整された直線距離が計算されると、コスト サーフェス、ソース特性、垂直方向ファクター、および水平方向ファクターにより、それらの距離単位を移動する速度を制御できます。 各ファクターは、調整された直線距離に対する乗数です。 ファクターの単位を指定する際は注意が必要です。 コスト サーフェスを好適度で示し、垂直方向ファクターを時間で示すことはできません。 単位は一致している必要があります。
一般に、コスト サーフェスは、速度解析の通行単位です。 垂直方向ファクター、水平方向ファクター、およびソース特性は、通常、コスト サーフェスのコスト単位の、単位のない乗数です。
これは、垂直方向ファクターを使用して Tobler のハイキング関数を適用する場合は該当しません。 ハイキング関数では、単位は時間で、コスト解析の通行単位になります。 解析にコスト サーフェスを追加する場合、コスト サーフェスの値は、垂直方向ファクターで傾斜角を表す一方で地表の移動時間を変更する、単位のない乗数でなければなりません。
ModelBuilder を使用してコスト サーフェスを作成します。
は、コスト サーフェスを効果的に作成できる環境です。 入力および出力する条件とジオプロセシング ツールを連結する機能があります。 モデルのグラフィックス表現により、モデルのロジックを視覚的に表すことができ、いつでもモデルを変更したり再実行することができます。
さまざまな目的を持つ複雑なコスト サーフェスの作成では、多くの場合、サブモデルが使用されます。 サブモデルは、モデルの目的を整理するだけでなく、特定条件がさまざまな移動目的に合うよう異なる変換を使用できます。 たとえば、ボブキャットの例では、土地利用タイプを変換する際、リソース サブモデルの場合は草地の縁近くの移動は有利ですが、セキュリティ サブモデルの場合は不利になる可能性があります。
コスト サーフェスのその他の用途
コスト サーフェスをその他の用途でどのように使用できるかを、以下で説明します。
徐行区域
コスト サーフェスを使用して、港の徐行区域を移動する際の最高ペースを表すことができます。 海岸線の周囲 100 メートルの安全圏での最高速度は 5 ノット、最高ペースは 1h/(5*1.852)km とすることができます。 100 ~ 200 メートルの安全圏コリドーでは、最高ペースを 1h/(10*1.852)km とすることができます。 速度が増すとペースは落ちます。
道路の建設費
新しい道路の建設費の総額を見積もるため、1 マイルあたりの建設費をコード化するコスト サーフェスを作成できます。 片側 1 車線対面通行の道路を新設する場合、同じ道路の建設でも、田園地域のほうが都市部より費用が少なくなります。 この場合は、コスト サーフェスのセルを分類して都市部と田園地域に分けることができます。 ARTBA (American Road and Transportation Builders Association) の FAQ の情報によれば、1 マイルあたりのコストは、田園地域のセルで通常 200 万ドル、都市部のセルで 400 万ドルとなっています。 さらに、地域ごとの土地利用や土地所有の法律に基づいてバリアが加わる可能性があります。
参考情報
以下のセクションでは、コスト サーフェスに関するその他の情報を提供します。
移動時期の考慮
時期によってコスト サーフェスが変わる可能性があります。 そのコスト サーフェスは、冬と夏、あるいは乾季と雨季のどちらの時期に移動することを想定していますか。 晴天と悪天候、あるいは異常な天候と典型的な天候のどちらの状態での移動を想定していますか。
移動にあたり、その他の時間的な影響がありますか。 野生生物のコスト解析で、出産場所に近づくための移動、あるいは生息地域間の毎日の移動か季節的な移動のいずれを想定していますか。 狩猟シーズンの移動ですか。
移動に影響を与える可能性があるさまざまな時間的ファクターは、変換や重み付けのみならず、コスト サーフェスで使用される条件にも影響する場合があります。
さまざまな季節的なタイプや移動タイプを取り込むため、場合によっては複数のコスト サーフェスを用意し、それぞれについて距離解析を実行する必要があります。 完全に年に 1 度の移動の必要性を取り込むため、結果を結合する必要が生じる場合があります。
コスト サーフェスへの道路やトレイルの組み込み
全地形対応車両 (ATV) で、負傷したハイカーの救助に向かう救助隊が使用するコスト サーフェスを考えてみましょう。 この例では、条件は、土地利用タイプ、傾斜方向、および傾斜角です。 湿地エリアではコストが高く、草地ではコストが低くなります。 春の救助なので、南向きの傾斜方向はぬかるんでコストがより高く、凍結した北向きの傾斜方向はコストが低くなります。 傾斜を移動する労力は、垂直方向ファクターによって取り込むことができます。
道路を移動する場合はコストが変わります。 道路では、より速く容易に移動できます。 道路を移動するコストは、一定した低コストです。
道路の一定した低コストを取り込むため、コスト サーフェスを作成後、道路をコスト サーフェスに組み込みます。
- [ラスター → ポリライン (Raster To Polyline)] ツールを使用して道路をラスター化し、道路に単一コストを割り当てます。 道路フィーチャ データセットにコスト フィールドがない場合は、FID などの 0 以上の値のフィールドをラスター化し、[ラスター演算 (Raster Calculator)] ツールで次の式を実行します。Con(rasterRoads >= 0, 50)
50 は、割り当てられたコストです。 得られたラスターは、roadCostValue という名前で、次の手順の式への入力として使用されます。
道路タイプがある場合は、道路タイプごとにコストが変わる可能性があります。
- [ラスター演算 (Raster Calculator)] ツールのリストの [Con] および [IsNull] ツールを使用して、NoData の値を 0 に変換します。 Con(IsNull(roadCostValue), 0, roadCostValue) という形式の式を使用します。
得られたラスターは、roadCost という名前で、次の手順の式への入力として使用されます。
- [ラスター演算 (Raster Calculator)] を使用して、コスト サーフェスに道路を組み込みます。 Con(roadCost > 0, roadCost, costSurface) という形式の式を使用します。
最終出力ラスターで、道路が通過するセルは、その道路に関連するコストが割り当てられます。 道路がないセルはすべて、コスト サーフェスで作成されたコスト値が割り当てられます。
この結果、地表を移動する ATV は、道路があればできるだけ長く道路上を移動し、負傷したハイカーに近づくために最終的に道路を外れます。 道路のコストは、勾配が急な場所やカーブが多い場所でより細かく調整できます。
バリアを厚くすることでの亀裂回避
コスト サーフェスには、道路や河川など、コストが高いあるいはバリアとなる線形フィーチャを取り込むことができます。 線形フィーチャがポリラインの場合はラスター化されます。 線形フィーチャは、ラスターとして表された場合、1 セル分の厚さになります。 バリアの性質は、完全に水平または垂直である場合は保持されますが、斜めになる場合があります。 このとき、移動者がバリアの亀裂に相当するものをすり抜けることが幾何学的に起こり得ます。 その場合、バリアまたはコストが高いセルは、移動にとってもはや障害物ではありません。

コスト サーフェスに線形フィーチャを追加するには、次の手順を実行します。
- [バッファー (Buffer)] ツールを使用して、少なくともコスト サーフェスのセルの対角線より長い線形フィーチャをバッファー処理します。
- [ポリゴン → ラスター (Polygon to Raster)] ツールを使用して、バッファー処理されたフィーチャをラスター化します。
- バッファー処理され、ラスター化されたすべてのセルにコストを割り当て、NoData のすべてのセルにゼロを割り当てます。 [ラスター演算 (Raster Calculator)] ツールを使用して、「Con(IsNull(buffRaster), 0, 35)」の形式で式を入力します。
値 35 は、線形フィーチャのコストです。
線形フィーチャが true バリアである場合は、前の式の false ステートメント (35) に何も指定しないことで、バッファー処理されたセルを NoData に設定します。
- ステップ 3 で得られたラスターを、前のセクションで説明したようにコスト サーフェスに追加します。
入力線形フィーチャがラスターの場合は、これらの同じ手順が使用されます。 線形ラスター フィーチャを最初にラスター化する必要はありません。 [距離累積 (Distance Accumulation)] ツールを使用し、[最大累積] (距離) の値を設定して、ラスター フィーチャの周囲にバッファーを作成します。
線形フィーチャがラスターではない場合は、バッファー処理する代わりに、ラスター化することができます。 続いて、統計情報を指定して、ラスター化した線形フィーチャで [フォーカル統計 (Focal Statistics)] ツールを実行します。 3 x 3 の近傍が選択されている場合、ツールは線形フィーチャの両側を 1 セル分広げます。 割り当てられるセル値は、指定した統計情報に基づきます。 出力されたサーフェスは、前のセクションで説明したようにコスト サーフェスに追加できます。 この方法は、線形フィーチャがラスターで、深さ、塩分濃度、pH、距離などのグラデーションを表す場合に便利です。
注意:
相対コスト スケールの線形フィーチャに高いコストが割り当てられる場合、割り当てられるコストは必ず、最終的なコスト サーフェスの合計値に対して相対的であるようにします。
ただし、その線形フィーチャが true バリアの場合は、コスト サーフェスで結合する前に、セルに NoData を割り当てます。 線形フィーチャが true バリアの場合は、[距離累積 (Distance Accumulation)] ツールでバリア パラメーターを使用して入力することをお勧めします。
適合性モデラーによるコスト サーフェスの作成
コスト サーフェスは個々のジオプロセシング ツールを使用して作成できますが、後で変更できるよう使用ツールや指定パラメーターを記録しておく必要があります。 コスト サーフェスを作成する場合は、ModelBuilder の使用をお勧めします。
コスト サーフェスは、Spatial Analyst 適合性モデラーでも作成できます。 Suitability Modeler を使用してコスト サーフェスを作成している場合、適合性モデルで、条件値が適切であるほど、割り当てられる適合性が高くなることに注意してください。 コスト サーフェスを使用して最小コスト解析が実行されます。 移動が容易でコストが低いエリアほど、低い値が割り当てられます。
Suitability Modeler の [個別カテゴリ] および [クラスの範囲] 変換法では、コスト値はカテゴリまたはクラスに 1 対 1 で割り当てられます。 [連続的な関数] 変換法では、適合性モデルで変換するのではなく、反対の関数を適用する必要があります。 たとえば、適合性モデルで河川に近いほうがより好適である場合は、[Small] 変換関数を使用することができます。 小さいあるいは近い場所ほど、適合性の値が大きくなります。 コスト サーフェスで河川近くの移動のほうがより好適または低コストの場合は、[Large] 関数を選択できます。 遠く離れた場所ほど、高い値、つまり、コストがより高い値が割り当てられます。 近い場所ほど低い値が割り当てられます。つまり、より低コストで移動に適していることを示す値です。
または、連続関数を選択する際、適合性モデルのときと同じロジックを使用することができます。 より好適な場所にはより高い値が割り当てられますが、コスト サーフェスでは、移動により好適な場所はより低い値が割り当てられます。 コスト サーフェスの値を逆にするには、[連続関数] 方法の [関数の反転] パラメーターを使用します。