[関数によるリスケール (Rescale by Function)] ツールは、指定された変換関数に基づいて入力ラスター値のスケールを変更します。 さまざまな変換関数があり、各関数は計算やアプリケーションによって変わります。 どの変換関数を使用するかは、どの関数が対象の現象を最もよく捉えているかによって決まります。 さらに、一連の入力パラメーターを介して、各関数の特性を調整することができます。
このセクションの情報を最大限に活用するには、このツールで使用される基本用語を十分に認識しておくことが役立ちます。 変換関数の下限と上限がどのように出力値に影響を与えるかを理解するには、「出力値に対する下限と上限の相互関係」をご参照ください。
関数のリスト
各関数を、以下の表にまとめます。表の各関数のリンクをクリックすると、その関数の説明を参照できます。
入力値が増えるにとともに優先度が増加する場合に使用されます。入力値が大きくなるに従って、さらに急激に優先度が増加します。 | |
特定の入力値の周辺で最も優先度が高くなり、入力値がその値から変動するに従って優先度が減少する場合に使用されます。 | |
入力値が大きいほど優先度が高くなることを示す場合に使用されます。 | |
線形関数を使用して入力値のスケールを変更します。 | |
入力値が低い場合は入力値が増えるに従って優先度が急激に増加し、入力値がさらに増えると増加する割合が減衰する場合に使用されます。 | |
最も小さい入力の優先度が最も高い場合に使用されます。 入力値が増えるに従って優先度が急激に減少し、入力値がさらに増えると優先度が減少する割合が減衰します。 | |
最も大きい入力の優先度が最も高い場合に使用されます。 入力値が増えるに従って優先度が急激に増加し、入力値がさらに増えると優先度が増加する割合が減衰します。 | |
平均と標準偏差に基づいて入力データのスケールを変更します。入力ラスターの値が大きいほど、優先度が高くなります。 | |
平均と標準偏差に基づいて入力データのスケールを変更します。入力ラスターの値が小さいほど、優先度が高くなります。 | |
中点に非常に近い入力値の優先度が高い場合に使用されます。 | |
入力値が増えるとともに入力値の優先度が急激に増加する場合に使用されます。 | |
入力ラスターの値が小さいほど優先度が高くなることを示す場合に使用されます。 | |
特定の入力値で最も優先度が高くなり、入力値がそのポイントから変動するに従って線形に優先度が減少する場合に使用されます。 |
関数の概要と説明
関数ごとに、概要、使用例、および関数曲線に対する特定の入力パラメーターの効果の詳細について説明しています。
概要
概要では、各関数の基本的な特性と具体的な動作について説明します。
使用例
使用例では、特定の関数が適している、具体的な実際の例について説明します。
パラメーターの効果
このセクションでは、形状制御パラメーターが関数に与える影響について説明します。 パラメーターの値の変更による曲線への影響について説明し、複数の異なるパラメーター値を使用してグラフをプロットして、その効果を示します。 Python クラス式も含まれ、グラフで示した変換関数の作成方法を示します。
注意:
ここで示す各グラフの例の入力は、0 〜 500 の値を含むラスターです。 この値が選択されている理由は特にありませんが、比較を容易にするため、すべてのグラフで一貫してこの値が使用されています。 実際に使用される入力ラスターは、任意の範囲の入力値を持つことができます。
Exponential 関数
概要
[Exponential] 関数は、指定されたシフト ファクターとベース ファクターを使用して指数関数を適用し、入力データを変換します。 適合性モデルでは、この関数は、低い入力値を持つ位置の優先度が最も低くなり、さらに大きな値を持つセルの位置では優先度が急激に増加する場合に使用するのが最も適しています。
使用例
亀の適合性モデルで、水源からの距離のスケールを変更する方法を検討してください。 亀は移動範囲が限られているため、水に近い場所を好みます。 水から遠い場所の優先度は、距離が増えるに従って急速に減少します。
パラメーターの効果
入力シフト
[入力シフト] は、入力値から引かれる値です。 Exponential 関数は、シフトされた入力値に適用されて関数値を決定します。
ベース ファクター
[ベース ファクター] パラメーターは、Exponential 関数が増加する傾きを制御します。 ベース ファクターを増やすと、小さい入力値では値が増えたときの優先度は緩やかに増加し、大きい入力値では優先度が急激に増加するようになります。 入力データの範囲が小さく (たとえば、0 〜 1)、最小値と最大値の間で指数曲線を維持したい場合に、このパラメーターを変更すると役立ちます。
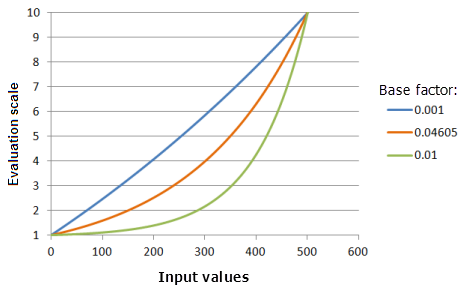
上のグラフで使用された関数:
- TfExponential(0.002651, BaseFactor, 0, 1, 500, 10)
ここで、BaseFactor に使用された値は、0.001、0.04605、および 0.01 です。 [シフト] の 0.002651 および [ベース ファクター] の 0.04605 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されたパラメーター値です。
Gaussian 関数
概要
[Gaussian] 関数は、正規分布を使用して入力値を変換します。 増加する評価スケールを適用した場合、正規分布の中点によって最も優先度の高い値が定義されます。 中点が最小閾値と最大閾値の間にある場合、その中点に等しい入力値は、[終点スケール] 値に割り当てられます。 残りの入力値の評価スケール上の値は、入力値が中点からいずれかの方向に変動するに従って、[起点スケール] 値に達するまで減少します (優先度の減少)。 適合性モデルでは、この関数は、最高の優先度が既知の値の近くにあり、入力値がその値から変動するに従って優先度が減少する場合に最も役立ちます。
使用例
ソーラー パネルを設置する場合、出力を最大化するには、パネルを正しい方向に向けることが重要です。 北半球の場合、南向きの角度 (180 度) の優先度が最も高くなります。 パネルが東や西に向くに従って連続的に優先度が減少し、北を向いた時点で優先度が最低になります。
パラメーターの効果
中点
[中点] パラメーターは、ガウス曲線の中央を定義します。 関数の中点をデータの中点からずらし、小さい値または大きい値の重要度を大きくまたは小さくしたい場合があります。 中点を移動する別の理由は、データの範囲外の基準値に関数を合わせるためです。
中点によって、関数曲線が広がる入力値の範囲を制御できます。
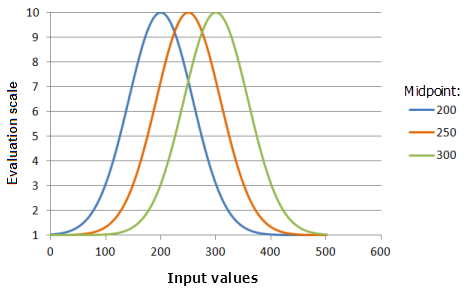
上のグラフで使用された関数:
- TfGaussian(Midpoint, 0.000147, 0, 1, 500, 10)
ここで、Midpoint) に使用された値は、200、250、および 300 です。 [中点] の 250 および [拡散] の 0.0000147 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されたパラメーター値です。
拡散
[拡散] パラメーターは、中点から減少する傾きを制御します。 この値を大きくすると、中点の周辺の曲線が狭くなります (優先度がより急速に減少します)。
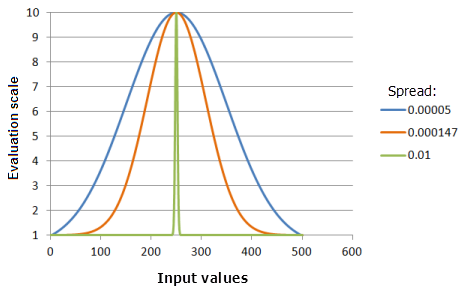
上のグラフで使用された関数:
- TfGaussian(250, Spread, 0, 1, 500, 10)
ここで、Spread に使用された値は、0.00005、0.000147、および 0.01 です。 [中点] の 250 および [拡散] の 0.0000147 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されたパラメーター値です。
Large 関数
概要
[Large] 変換関数は、入力値が大きいほど優先度が高くなる場合に使用されます。 中点を定義することで、関数の遷移点が指定されます。 値が中点よりも大きくなると優先度が増加し、値が中点よりも小さくなると優先度が減少します。 中点から変動した際に優先度が増加または減少する割合は、[拡散] 形状制御パラメーターによって決定されます。
使用例
商品取引の適合性モデルを作成する際に、コーヒー生産量の条件のスケールを変更したい場合があります。 生産量の大きい場所は、優先度が高くなります。この優先度は、生産量の増加とともに非線形に増加します。
パラメーターの効果
中点
[中点] は、関数の遷移点を定義します。 この値を入力データの中点よりも小さくなるようにシフトすると、遷移点が変更されます。その結果、中点の右側の値の大きい範囲で優先度が増加し、優先度が増加する割合が大きくなります。
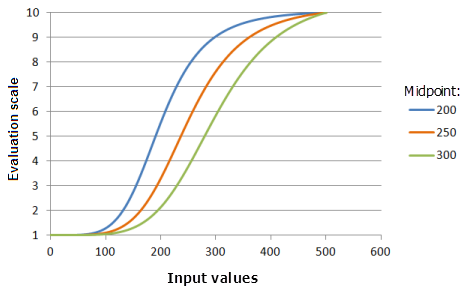
上のグラフで使用された関数:
- TfLarge(Midpoint, 5, 0, 1, 500, 10)
ここで、Midpoint に使用された値は、200、250、および 300 です。 [中点] の 250 および [拡散] の 5 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
拡散
[拡散] パラメーターは、優先度が増加または減少する割合を制御します。 拡散の値を増やすと、中点よりも大きい入力値の優先度が最大閾値に向かって増加する割合が大きくなり、中点よりも小さい入力値の優先度が最小閾値に向かって減少する割合が大きくなります。
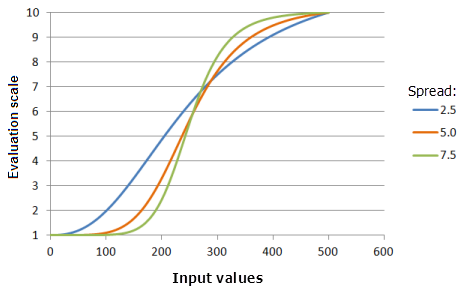
上のグラフで使用された関数:
- TfLarge(250, Spread, 0, 1, 500, 10)
ここで、Spread に使用された値は、2.5、5.0、および 7.5 です。 [拡散] の 5 および [中点] の 250 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
Linear 関数
概要
[Linear] 変換関数は、指定された最小値と最大値間で線形関数を適用します。 [起点スケール] が [終点スケール] よりも大きい場合は、負の線形関係 (負の傾き) が設定されます。
この関数は、値の優先度が一定の線形な割合で増加または減少する場合に使用するのが最も適しています。
使用例
野生生物の生息地の気候変化の適合性モデルを作成する際に、野生生物が好む場所の評価値のスケールを変更する必要がある場合があります。 分析範囲内では、評価値が大きいほど優先度が高くなります。
パラメーターの効果
最小
[最小値] パラメーターで、Linear 関数が通過する最初の点を指定します。 基準に対する現象の優先度に対応するように、パラメーター値を入力データの最小値から変更できます。
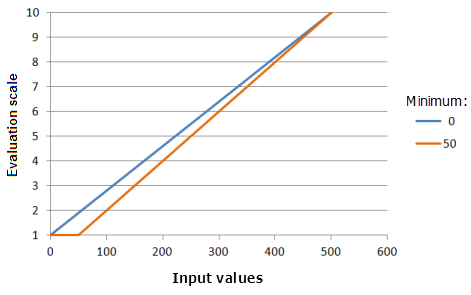
上のグラフで使用された関数:
- TfLinear(Minimum, 500, 0, 1, 500, 10)
ここで、Minimum に使用された値は、0 および 50 です。 [最小値] の 0 および [最大値] の 500 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
最大
[最大値] パラメーターで、Linear 関数が通過する 2 番目の点を指定します。 基準に対する現象の優先度に対応するように、パラメーター値を入力データの最大値から変更できます。
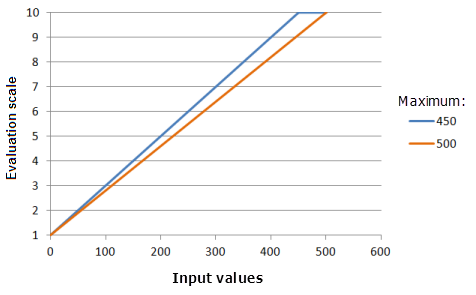
上のグラフで使用された関数:
- TfLinear(0, Maximum, 0, 1, 500, 10)
ここで、Maximum に使用された値は、450 および 500 です。 [最小値] の 0 および [最大値] の 500 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
Logarithm 関数
概要
[Logarithm] 変換関数は、指定されたシフトとファクターを使用して、入力データに対数関数を適用します。 適合性モデルでは、Logarithm 関数は、優先度が急激に増減し、その後で入力基準値が大きくなるとともに変化の割合が減少する場合に使用するのが最適です。
使用例
鳥の適合性モデルを作成する際に、餌の量の条件のスケールを変更したい場合があります。 鳥が生存できないほど餌の量が少ない場所の優先度は、最低になります。 鳥の生存に十分な量の餌がある場合、餌の量が増えるにつれて鳥の生息への適性も高まるため、その場所の優先度が急激に増加します。 ある点で、鳥の餌の量は十分になります。そのため、餌の量がそれより増えても、優先度は高くなりますが、増加する割合は非常に遅くなります。
パラメーターの効果
シフト
[シフト] は、入力値から引かれる値です。これによって、対数計算を開始する入力値を制御できます。 たとえば、鳥の使用例では、餌が 250 単位よりも少ない場所で鳥が生存できない場合、関数の始点を 250 にずらすことができます。
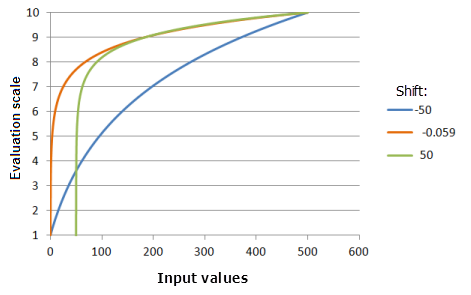
上のグラフで使用された関数:
- TfLogarithm(Shift, 0.0046, 0, 1, 500, 10)
ここで、Shift に使用された値は、-50.0、-0.059、および 50.0 です。 [シフト] の -0.059 および [指数] の 0.0046 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されたパラメーター値です。
ファクター
[ファクター] は、対数関数値の増加を制御する乗数です。 入力値の範囲が狭い場合 (たとえば、0 〜 1)、最小値と最大値の間で対数曲線を維持するように、このパラメーターを変更できます。
Logistic Decay 関数
概要
[Logistic Decay] 変換関数は、定義された Y インターセプトの割合を使用して、ロジスティック減少関数を指定された最大値と最小値の範囲内に合わせます。 適合性モデルでは、Logistic Decay 関数は、入力値が小さいほど優先度が高くなる場合に使用するのが最も適しています。 入力値が増えるに従って、優先度が急激に減少し、優先度が最低になる点に達すると、その点よりも大きい入力値の優先度は一定になります。
使用例
住宅適合性モデルを作成する際に、送電線からの距離による電気コストの条件のスケールを変更したい場合があります。 既存の送電線に近い場所は、その場所に電気を引く際のコストが下がるため、優先度が高くなります。 一定の距離を超えると、追加の変圧器を設置する必要があり、作業と機器による追加のコストが発生するため、優先度が急激に減少します。 最も遠いセルは、その場所のコストがすでに大きすぎるため、優先度に対する追加コストの影響をあまり受けません。そのため、その場所では、優先度が一定になります。
パラメーターの効果
最小
[最小値] パラメーターは、ロジスティック減少曲線の減少の始点を制御します。 [最小値] が大きくなるほど、関数の主要な減少部分での優先度の減少が大きくなります (曲線の傾きが大きくなります)。
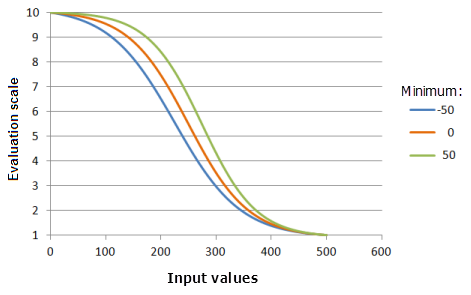
上のグラフで使用された関数:
- TfLogisticDecay(Minimum, 500, 99, 0, 1, 500, 10)
ここで、Minimum に使用された値は、-50、0、および 50 です。 [最小値] の 0、[最大値] の 500、および yInterceptPercent の 99 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
最大
[最大値] パラメーターは、ロジスティック減少曲線の減少の終点を制御します。 [最大値] が小さいほど、関数の主要な減少部分での優先度の減少が大きくなります (曲線の傾きが大きくなります)。
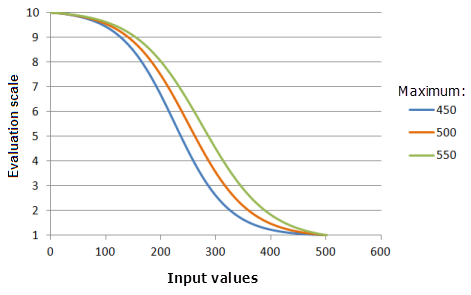
上のグラフで使用された関数:
- TfLogisticDecay(0, Maximum, 99, 0, 1, 500, 10)
ここで、Maximum に使用された値は、450、500、および 550 です。 [最小値] の 0、[最大値] の 500、および yInterceptPercent の 99 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
Y インターセプトの割合
[Y インターセプトの割合] パラメーターは、ロジスティック減少曲線の減少部分に含まれる値の範囲を決定します。 概念的に、Logistic Decay 関数は「S」字を反転した形状として考えることができます。 「S」字の本体に 2 つの尾が接続されており、曲線の減少部分と呼ばれます。 このパラメーター値を大きくすると、曲線の減少部分に含まれる入力値の範囲が狭くなります (「S」字がより直立する) が、値の優先度が減少する割合が大きくなり、曲線がより顕著になります。
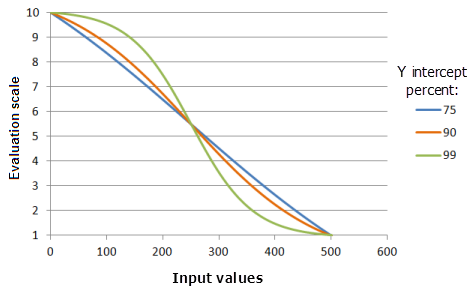
上のグラフで使用された関数:
- TfLogisticDecay(0, 500, YInterceptPercent, 0, 1, 500, 10)
ここで、Y インターセプトの割合に使用された値は、75、90、および 99 です。 [最小値] の 0、[最大値] の 500、および yInterceptPercent の 99 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
Logistic Growth 関数
概要
[Logistic Growth] 変換関数は、LogisticDecay 変換関数に類似していますが、Logistic Growth 関数の場合、優先度が減少するのではなく増加する点が異なります。
使用例
生息地の適合性モデルでは、動物の優先度は、利用できる餌が増えるとともにロジスティックに増加します。 まず、餌の量は、生存ための最低限のレベルに達する必要があります。その後、餌が増えるとともに優先度が急激に増加し、最大摂取量に達すると、その点で優先度が一定になります。
パラメーターの効果
最小
[最小値] パラメーターは、ロジスティック増加関数の増加の始点を制御します。 [最小値] が大きくなるほど、関数の主要な増加部分での優先度の増加が大きくなります (曲線の傾きが大きくなります)。
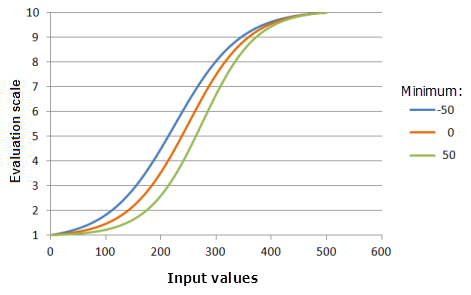
上のグラフで使用された関数:
- TfLogisticGrowth(Minimum, 500, 1, 0, 1, 500, 10)
ここで、Minimum に使用された値は、-50、0、および 50 です。 [最小値] の 0、[最大値] の 500、および [yInterceptPercent] の 1 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
最大
[最大値] パラメーターは、ロジスティックな増加の終点を制御します。 [最大値] が小さいほど、関数の主要な増加部分での優先度の増加が大きくなります (曲線の傾きが大きくなります)。
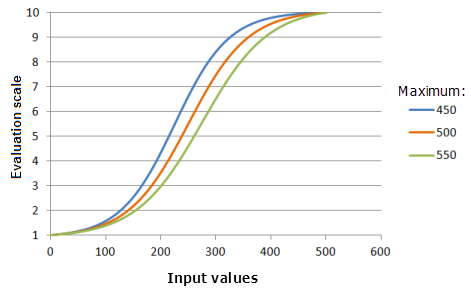
上のグラフで使用された関数:
- TfLogisticGrowth(0, Maximum, 1, 0, 1, 500, 10)
ここで、Maximum に使用された値は、450、500、および 550 です。 [最小値] の 0、[最大値] の 500、および yInterceptPercent の 1 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されるパラメーター値です。
Y インターセプトの割合
[Y インターセプトの割合] パラメーターは、ロジスティック増加曲線の増加部分に含まれる値の範囲を決定します。 概念的に、Logistic Growth 増加関数は「S」字の形状として考えることができます。 「S」字の本体に 2 つの尾が接続されており、曲線の増加部分と呼ばれます。 yInterceptPercent の値を小さくすると、曲線の増加部分に含まれる入力値の範囲が狭くなります (「S」字がより直立する) が、値の優先度が増加する割合が大きくなり、曲線がより顕著になります。
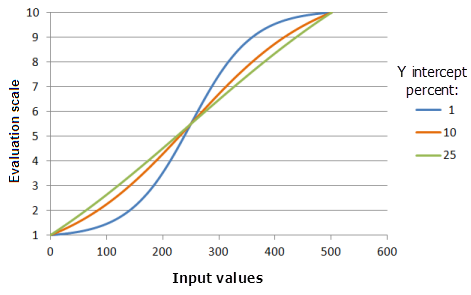
上のグラフで使用された関数:
- TfLogisticGrowth(0, 500, YInterceptPercent, 0, 1, 500, 10)
ここで、Y インターセプトの割合に使用された値は、1、10、および 25 です。 [最小値] の 0、[最大値] の 500、および [yInterceptPercent] の 1 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
MSLarge 関数
概要
[MSLarge] 変換関数は Large 変換関数に類似していますが、関数の定義が、指定された平均と標準偏差の乗数に基づく点が異なります。 一般に、これら 2 つの関数の違いは、非常に大きい値の優先度が高い場合に、MSLarge 関数の方が適している点です。
平均と標準偏差の乗数の特定の組み合わせを指定した場合、この関数の結果は Large 変換関数とほぼ同じになります。
使用例
Large 変換関数の使用例で説明した商品取引の適合性モデルに類似していますが、この場合はコーヒー生産量の大きい場所の優先度が非常に高くなる点が異なります。
パラメーターの効果
平均乗数
[平均乗数] パラメーターは、関数の曲線の傾きを制御します。 この乗数を減らすと、大きい入力値では優先度の高い部分の範囲が広がり、値が大きくなるとともに関数曲線が減少する割合が少なくなり、最大閾値に達します。
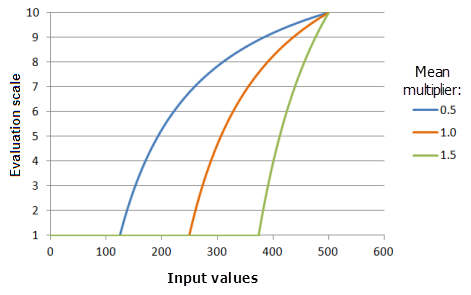
上のグラフで使用された関数:
- TfMSLarge(MeanMultiplier, 1, 0, 1, 500, 10)
ここで、平均に使用された値は、0.5、1.0、および 1.5 です。 [平均乗数] の 1 および [標準偏差の乗数] の 1 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
標準偏差の乗数
[標準偏差の乗数] パラメーターは、関数の曲線の傾きを制御します。 この乗数を増やすと、関数曲線が増加する割合が減少します。
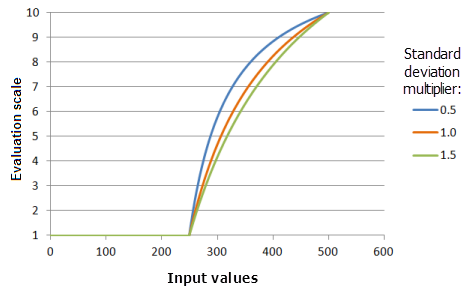
上のグラフで使用された関数:
- TfMSLarge(1, StandardDeviationMultiplier, 0, 1, 500, 10)
ここで、標準偏差に使用された値は、0.5、1.0、および 1.5 です。 [平均乗数] の 1 および [標準偏差の乗数] の 1 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
MSSmall 関数
概要
[MSSmall] 変換関数は Small 変換関数に類似していますが、関数の定義が、指定された平均と標準偏差の乗数に基づく点が異なります。 一般に、これら 2 つの関数の違いは、非常に小さい値の優先度が高い場合に、MSSmall 関数の方が適している点です。
平均と標準偏差の乗数の特定の組み合わせを指定した場合、この関数の結果は Small 変換関数とほぼ同じになります。
使用例
Small 変換関数で説明した住宅の適合性モデルでの道路からの距離に基づく建築コストの基準のスケール変更に類似していますが、この場合はセルの位置が道路に近づくと優先度が非常に高くなる点が異なります。
パラメーターの効果
平均乗数
[平均乗数] パラメーターは、関数の曲線の傾きを制御します。 この乗数を減らすと、小さい入力値では優先度の高い範囲が広がり、値が大きくなるとともに関数曲線が減少する割合が大きくなり、最大閾値に達します。
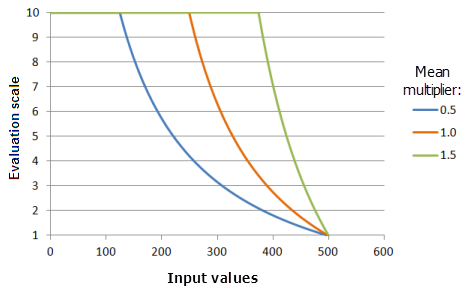
上のグラフで使用された関数:
- TfMSSmall(MeanMultiplier, 1, 0, 1, 500, 10)
ここで、平均に使用された値は、0.5、1.0、および 1.5 です。 [平均乗数] の 1 および [標準偏差の乗数] の 1 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
標準偏差の乗数
[標準偏差の乗数] パラメーターは、関数の曲線の傾きを制御します。 この乗数を増やすと、関数曲線が減少する割合が減ります。
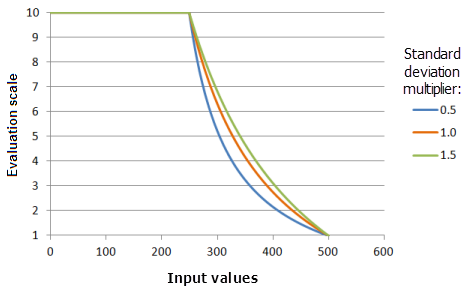
上のグラフで使用された関数:
- TfMSSmall(1, StandardDeviationMultiplier, 0, 1, 500, 10)
ここで、標準偏差に使用された値は、0.5、1.0、および 1.5 です。 [平均乗数] の 1 および [標準偏差の乗数] の 1 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
Near 関数
概要
[Near] 変換関数は、最高の優先度が特定の値に近接している場合に最も役立ちます。 中点が最小閾値と最大閾値の間にある場合、その中点に等しい入力値は、[終点スケール] 値に割り当てられます。 残りの入力値の評価スケール上の値は、入力値が中点からいずれかの方向に変動するに従って、[起点スケール] 値に達するまで減少します (優先度の減少)。
指定したパラメーターによっては、Near 変換関数と Gaussian 変換関数は類似している場合があります。 通常、Near 関数は、Gaussian 関数よりも広がる範囲が狭く、より大きな割合で減少します。 そのため、この関数は、中点に極めて近い値の優先度が高い場合に使用されます。
使用例
Gaussian 変換関数で説明した太陽電池パネルの適合性モデルと同様ですが、南向きの角度の優先度が非常に高い点が異なります。
パラメーターの効果
中点
[中点] は、Gaussian 関数の中点と同じく、関数曲線の中央を定義します。
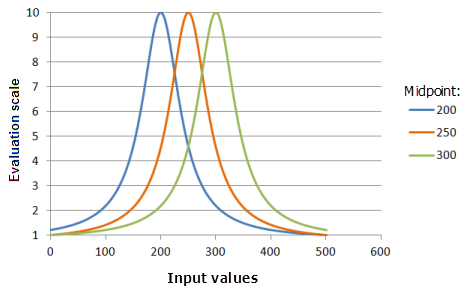
上のグラフで使用された関数:
- TfNear(Midpoint, 0.000576, 0, 1, 500, 10)
ここで、Midpoint に使用された値は、200、250、および 300 です。 [中点] の 250 および [拡散] の 0.000576 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されたパラメーター値です。
拡散
[拡散] パラメーターは、Gaussian 関数の場合と同様ですが、入力値が中点から変動すると、より劇的な効果がある点が異なります。
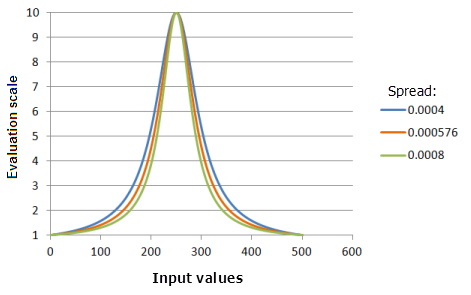
上のグラフで使用された関数:
- TfNear(250, Spread, 0, 1, 500, 10)
ここで、Spread に使用された値は、0.0004、0.000576、および 0.008 です。 [中点] の 250 および [拡散] の 0.000576 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されたパラメーター値です。
Power 関数
概要
[Power] 変換関数は、定義されたシフトを使用し、指定された指数で増加する累乗関数を入力データに適用します。 適合性モデルでは、Power 関数は、最小の入力値の優先度が最も低いが、入力値が増えるに従って優先度が増加し、さらに入力値が増えると優先度が急激に増加する場合に使用するのが最も適しています (この動作は、指数の値によって変わります)。
使用例
原子力発電所の場所を決める適合性モデルで、断層からの距離による安全条件のスケールの変更に使用できます。 場所が断層線から離れるに従って、累乗関数に基づいて連続的に優先度が増加します。つまり、断層線から離れた場所は、断層に近い場所と比較して、著しく優先度が高くなります。
パラメーターの効果
シフト
[シフト] パラメーターは、入力値から引かれる値です。これによって、累乗計算を開始する入力値を制御できます。 たとえば、原子力発電所の使用例で、断層線から 10 キロメートルの範囲内に原子力発電所を建設しないことを決めました。 Power 関数が 10 キロメートルから始まるように、関数をシフトできます。
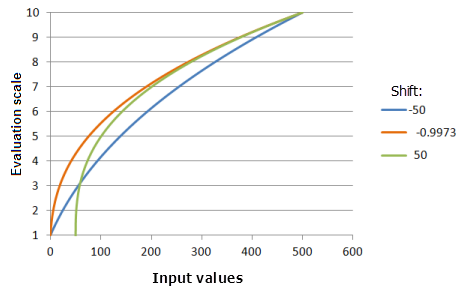
上のグラフで使用された関数:
- TfPower(Shift, 0.3704, 0, 1, 500, 10)
ここで、Shift に使用された値は、-50.0、-0.9973、および 50.0 です。 [シフト] の -0.9973 および [指数] の 0.3704 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されたパラメーター値です。
指数
[指数] パラメーターは、Power 関数が増加する傾きを制御します。 指数を大きくすると、特に入力値が大きいところで、関数曲線の傾きが大きくなります。
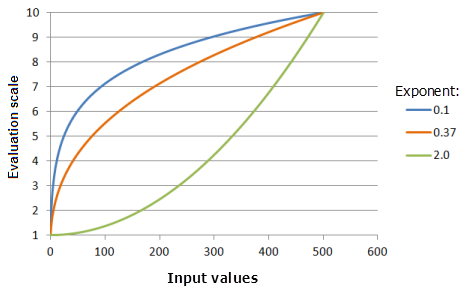
上のグラフの入力パラメーター:
- TfPower(-0.9973, Exponent, 0, 1, 500, 10)
ここで、Exponent に使用された値は、0.1、0.37、および 2.0 です。 [シフト] の -0.9973 および [指数] の 0.3704 は、入力データセットの範囲が 0 〜 500 の場合にデフォルトで計算されたパラメーター値です。
Small 関数
概要
[Small] 変換関数は、入力値が小さいほど優先度が高くなる場合に使用されます。 中点を定義することで、関数の遷移点が指定されます。 値が中点よりも大きくなると優先度が減少し、値が中点よりも小さくなると優先度が増加します。 中点から変動した際に優先度が増加または減少する割合は、[拡散] 形状制御パラメーターによって決定されます。
使用例
住宅の適合性モデルで、道路データセットまでの距離による建築コストの条件のスケールを変更したい場合があります。 場所が道路に近づく (値が小さい) ほど、優先度が高く (コストが低く) なります。道路からの距離が増えるに従って、優先度が連続的に減少します。
パラメーターの効果
中点
[中点] は、関数の遷移点を定義します。 この中点を入力データの中点よりも大きくなるようにシフトすると、遷移点が変更されます。その結果、中点の左側の値の小さい範囲で優先度が増加し、優先度が減少する割合が小さくなります。
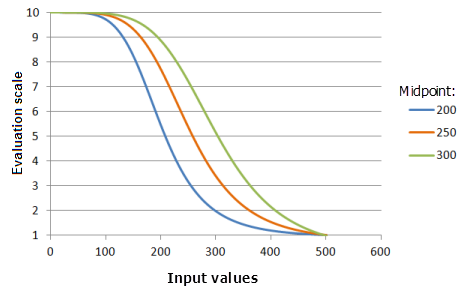
上のグラフで使用された関数:
- TfSmall(Midpoint, 5, 0, 1, 500, 10)
ここで、Midpoint に使用された値は、200、250、および 300 です。 [中点] の 250 および [拡散] の 5 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
拡散
[拡散] は、優先度が減少または増加する割合を制御します。 拡散の値を増やすと、中点よりも小さい入力値の優先度が最小閾値に向かって増加する割合が大きくなり、中点よりも大きい入力値の優先度が最大閾値に向かって減少する割合が大きくなります。
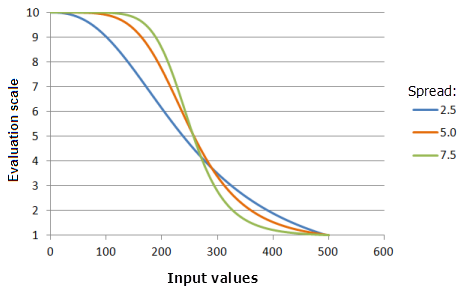
上のグラフで使用された関数:
- TfSmall(250, Spread, 0, 1, 500, 10)
ここで、Spread に使用された値は、2.5、5.0、および 7.5 です。 [中点] の 250 および [拡散] の 5 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
Symmetric Linear 関数
概要
[Symmetric Linear] 変換関数は、指定された最小値と最大値の間で線形関数を適用します。この線形関数は、[最小値] と [最大値] の中点で反転します。 反転する点に対応する入力値の優先度が最も高くなります。入力値の優先度は、反転する点から変動するに従って線形に減少します。 [最小値] を下回るが [最小閾値] を超えるすべての入力値、または [最大値] を超えるが [最大閾値] を下回るすべての入力値は、[起点スケール] に割り当てられます。
[最小値] が [最大値] よりも大きい場合は、負の線形関係 (負の傾き) が設定されます。
Symmetric Linear 関数は、最も高い優先度が中点の値にあり、入力値が中点から変動するに従って優先度が線形に増加または減少する場合に使用するのが最も適しています。
使用例
特定の病気を媒介する虫の活動が、華氏 70 度で最も低くなります。 分析範囲内の平均温度が、最低平均温度に向かって下がるか、最大平均温度に向かって上がるにつれて、この虫はより活動的になり、人間の病気の症例も多くなります。 地域のレクリエーション施設の場所を決める場合、平均温度が 70 度の領域が最も優先されます。分析範囲内の温度が 70 度から減少するに従って優先度が線形に減少して最小平均温度に達し、70 度から増加するに従って優先度が線形に減少して最大平均温度に達します。
パラメーターの効果
最小
[最小値] パラメーターで、SymmetricLinear 関数が通過するの点のうちの 1 つを指定します。 最小値を変更すると、関数が反転する場所である中点が変化します。 基準に対する現象の優先度に対応するように、入力ラスターの最小値から設定された最小値を変更できます。
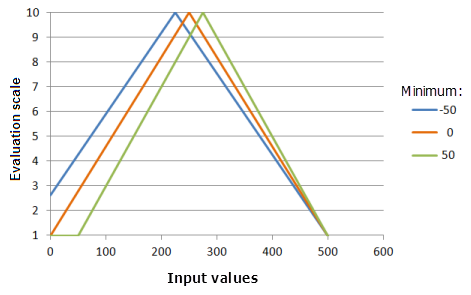
上のグラフで使用された関数:
- TfSymmetricLinear(Minimum, 500, 0, 1, 500, 10)
ここで、Minimum に使用された値は、-50、0、および 50 です。 [最小値] の 0 および [最大値] の 500 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。
最大
[最大値] パラメーターで、SymmetricLinear 関数が通過する 2 番目の点を指定します。 最大値を変更すると、関数が反転する場所である中点が変化します。 基準に対する現象の優先度に対応するように、入力ラスターの最大値から設定された最大値を変更できます。
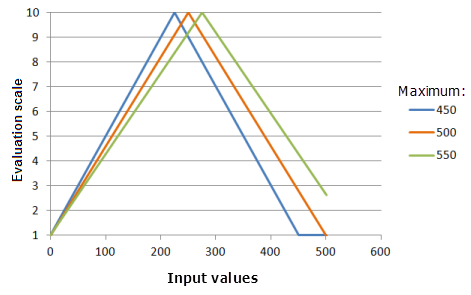
上のグラフで使用された関数:
- TfSymmetricLinear(0, Maximum, 0, 1, 500, 10)
ここで、Maximum に使用された値は、450、500、および 550 です。 [最小値] の 0 および [最大値] の 500 は、入力データセットの範囲が 0 〜 500 の場合のデフォルトのパラメーター値です。