La logique floue peut être employée comme technique d’analyse de superposition dans le cadre d’applications d’analyse de superposition traditionnelles, telles que la sélection de sites et les modèles d’adéquation.
Le principe de base derrière la logique floue est qu’il existe des imprécisions inhérentes aux attributs et à la géométrie des données spatiales. La logique floue propose des techniques qui permettent de résoudre les deux types d’imprécisions, mais se concentre sur les imprécisions des données attributaires dès lors qu’il s’agit de l’analyse de superposition. Les imprécisions des données attributaires apparaissent principalement dans la définition des classes et la mesure du phénomène. Ces deux sources d’imprécisions, et en particulier la définition des classes, sont susceptibles de générer des imprécisions lors de l’attribution des cellules à des classes spécifiques.
La définition des classes dans une classification et l’imprécision lors de l’attribution de phénomènes à des classes peuvent affecter la prise de décision. L’outil Superposition floue aide les décideurs à prendre des décisions au sujet de ces imprécisions. La logique floue se concentre sur la modélisation des imprécisions des limites de classe.
Les outils Superposition pondérée et Somme pondérée reposent sur des ensembles classiques, où chaque cellule est ou non une classe. La logique floue est particulièrement adaptée aux situations où les limites entre les classes ne sont pas claires. À la différence des ensembles classiques, la logique floue ne concerne pas l’appartenance ou la non-appartenance à une classe ; elle définit la possibilité d’appartenance du phénomène à un ensemble (ou classe). La logique floue repose sur la théorie des ensembles ; elle vous permet donc de définir des possibilités et non des probabilités.
Par exemple, dans un modèle d’adéquation pour des logements, si la pente est l’un des critères en entrée, chaque valeur de pente est transformée ou se voit attribuer une valeur comprise entre 0 et 1 indiquant la possibilité d’appartenance de cette valeur de pente à l’ensemble d’adéquation (ou classe) spécifiant l’adéquation du bâtiment. La valeur 1 indique la pleine certitude que la valeur figure dans l’ensemble et 0 indique de façon certaine qu’elle n’y figure pas. Toutes les autres valeurs correspondent à un certain degré de possibilité, les valeurs supérieures indiquant une vraisemblance plus élevée. Le processus de transformation des valeurs en entrée d’origine sur l’échelle de 0 à 1 de possibilité d’appartenance est appelé processus d’appartenance floue. Chaque critère du modèle, comme l’exposition, la distance par rapport aux routes et le type d’utilisation du sol, est soumis au processus d’appartenance floue. L’outil Appartenance floue permet de transformer les données sur une échelle de possibilité de 0 à 1.
L’outil Superposition floue est utilisé pour déterminer les localisations qui répondent le mieux à tous les critères, à savoir la vraisemblance de l’appartenance à tous les ensembles. Lorsque vous combinez plusieurs critères, l’outil Superposition floue explore la vraisemblance d’appartenance de la cellule par rapport à chaque ensemble défini par les critères multiples. Par exemple, quel est le degré de vraisemblance qu’une localisation particulière appartienne à l’adéquation favorable en termes de pente, d’exposition et de distance par rapport aux routes ?
L’analyse de superposition fait ainsi intervenir la logique floue lors de deux étapes principales : l’appartenance floue et l’analyse de superposition floue. Ces deux étapes correspondent respectivement aux étapes de reclassification/transformation et d’ajout/combinaison dans le processus général de superposition.
L’appartenance répétée à une classe n’est pas évidente, mais subjective. En langage humain, ces imprécisions sont qualifiées par des modificateurs, comme très, légèrement et modérément. La logique floue effectue l’analyse de superposition en procédant davantage comme la pensée humaine naturelle. Les choses ne sont pas claires et nettes ; les limites peuvent être floues. La logique floue n’est pas une analyse de l’incertitude des données. Elle explore l’imprécision des limites de classe.
Les sections suivantes abordent la classification des données, le processus d’appartenance floue et l’analyse de superposition floue. Vous trouverez également ci-dessous une comparaison de la logique floue aux techniques d’analyse de superposition pondérée et binaire, ainsi qu’une description de l’intégration de la logique floue dans le processus général de superposition.
Classification des données et logique floue
Pour décrire ou ordonner des phénomènes, il convient généralement de les caractériser selon des classes. La catégorie d’utilisation du sol, le type de sol, la pondération d’adéquation, la classe de route et le type de végétation sont tous les exemples de classes. Dans les ensembles classiques, l’appartenance est binaire : soit le phénomène se trouve dans la classe, soit il n’y figure pas. Les limites de classes sont nettes. Mais en raison de l’imprécision de la pensée, de règles ambiguës de catégorisation, du flou et de l’ambivalence, les limites entre les classes ne sont pas toujours claires.
Par exemple, si le phénomène que vous explorez est la relation des différentes tailles des personnes d’un groupe, vous pouvez commencer par agréger ces personnes en classes en fonction de leur taille. Vous pouvez commencer par trois classes : petite taille, taille moyenne et grande taille. Vous devez ensuite définir les limites de ces classes. Ainsi, vous pouvez considérer comme petites les personnes mesurant au maximum 5 pieds (1,524 mètre), comme grandes les personnes mesurant 6 pieds (1,8288 mètre) et plus, et comme moyennes les personnes mesurant entre 5 et 6 pieds (1,6764 et 1,8288 mètre). Si une personne mesure 6 pieds (1,8288 mètre), elle est placée dans la classe des personnes de grande taille. Si une personne mesure 5 pieds et 11 pouces (1,8034 mètre), elle est classée comme une personne de taille moyenne. Avec une différence de seulement 1 pouce (0,0254 mètre), ces deux personnes sont placées dans deux classes distinctes. Cette même relation de différence serait appliquée entre un autre membre du groupe mesurant 5 pieds et 1 pouce (1,5494 mètre) et un second membre de 6 pieds et 6 pouces (1 9812 mètre). En raison de la grossièreté des classifications, il n’est pas possible de capturer les relations entières entre les hauteurs.
Afin de décrire de manière plus appropriée les relations de hauteur entre les différentes personnes, il est possible d’ajouter davantage de classes. Vous pourriez ainsi ajouter deux classes supplémentaires : petite taille pour les personnes mesurant au maximum 4 pieds et 10 pouces (1,4732 mètre), taille moyennement petite pour les personnes mesurant entre 4 pieds et 10 pouces (1,4732 mètre) et 5 pieds et 4 pouces (1,6256 mètre), moyenne taille pour les personnes entre 5 pieds et 4 pouces (1,6256 mètre) et 5 pieds et 10 pouces (1,778 mètre), taille moyennement grande pour les personnes mesurant entre 5 pieds et 10 pouces (1,778 mètre) et 6 pieds et 4 pouces (1,9304 mètre), et grande taille pour les personnes mesurant plus de 6 pieds et 4 pouces (1,9304 mètre). Cet affinage des classes permet une capture plus précise de la relation entre les tailles des personnes.
Il est même possible d’ajouter encore plus de classes pour les affiner davantage. Quel que soit le nombre de classes ajoutées, la relation de taille entre les personnes est toujours généralisée. Il existe certains phénomènes qui ne peuvent pas être classés dans des classes strictement définies. Il est parfois difficile de regrouper le monde réel selon des classes discrètes.
Comme vous pouvez le constater, la définition de limites de classe peut être subjective et varier selon la définition du phénomène. Dans les classes de taille définies ci-dessus, les personnes sont supposées être des adultes, vraisemblablement un mélange d’hommes et de femmes. Les définitions des classes sont susceptibles de devoir être modifiées si le groupe est entièrement composé de femmes. Les limites des classes devront peut-être même être davantage modifiées si le groupe est composé d’enfants ou s’il en inclut.
La définition des classes et les caractéristiques du phénomène déterminent le mode de représentation du phénomène modélisé. Les erreurs de mesure aggravent encore davantage le problème des classifications. Si la procédure de mesure de la taille des personnes est précise à plus ou moins 1 pouce (0,0254 mètre), l’imprécision peut attribuer une autre classe au phénomène.
La logique floue modélise cette imprécision dans le processus de classification. Dans la logique floue, les classes sont définies comme des ensembles. Il est nécessaire de comprendre la valeur idéale d’appartenance à l’ensemble. Par exemple, la valeur de pente idéale dans un modèle d’adéquation pour des logements. Plus les valeurs s’éloignent de la valeur idéale, plus le niveau de clarté diminue jusqu’à un certain point où il est clair que la valeur n’appartient pas à l’ensemble (ainsi, la pente peut être de façon certaine trop raide pour permettre la construction).
Si l’on reprend l’application de mesure des tailles précédente avec les trois classes de taille initiales (petite taille, taille moyenne et grande taille), la logique floue peut permettre le chevauchement de ces classes.
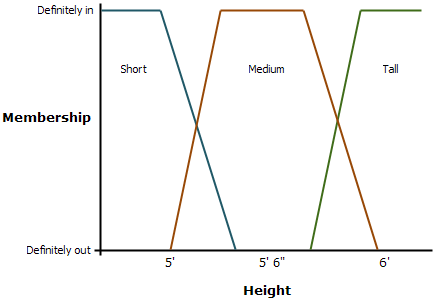
Dans l’image ci-dessus, l’appartenance pleine et entière à chaque classe est définie comme suit :
- Petite taille : < 5 pieds (1,524 mètre)
- Taille moyenne : 5 pieds 3 pouces 1/2 (1,6129 mètre) à 5 pieds 8 pouces 1/2 (1,7399 mètre)
- Grande taille : > 6 pieds (1,8288 mètre)
Pour l’ensemble (ou la classe) Petite taille, toute personne mesurant au maximum 5 pieds (1,524 mètre) est de façon certaine considérée comme appartenant à l’ensemble et se voit attribuer la valeur 1. Toute personne mesurant entre 5 pieds (1,524 mètre) et 5 pieds et 3 pouces 1/2 (1,6129 mètre) se trouve entre les ensembles (ou classes) Petite taille et Taille moyenne. Les personnes mesurant entre 5 pieds (1,524 mètre) and 5 pieds 1 pouce 3/4 (1,6193 mètre) se situent plus vraisemblablement dans l’ensemble Petite taille. Les personnes mesurant plus de 5 pieds et 1 pouce 3/4 (1,6193 mètre) et pas plus de 5 pieds et 3 pouces 1/2 (1,6129 mètre) peuvent appartenir à l’ensemble Petite taille, mais ont une possibilité plus importante d’appartenir à l’ensemble Taille moyenne.
Le processus d’appartenance floue est généralement implémenté via des fonctions prédéterminées à l’aide de l’outil Appartenance floue.
Appartenance floue
Le processus d’appartenance floue caractérise l’imprécision des classes de phénomènes qui ne possèdent pas de limites clairement définies.
Lors de ce processus, les valeurs d’origine du phénomène sont converties en possibilité d’appartenance à un ensemble défini. L’ensemble défini peut répondre à une problématique d’adéquation, de localisation au sein d’un rayon de distance favorable ou de possibilité de découverte d’une ressource minérale spécifiée. Les valeurs d’origine du phénomène sont reclassées en fonction de ce continuum d’appartenance via des fonctions d’appartenance floue prédéfinies ou grâce à d’autres techniques de reclassification.
Lors du processus d’appartenance floue, la définition idéale de l’appartenance à l’ensemble est définie. Chaque valeur du phénomène centrale par rapport au cœur de la définition de l’ensemble se voit attribuer la valeur 1. Les valeurs qui ne font, avec certitude, pas partie de l’ensemble se voient attribuer la valeur 0. Les valeurs comprises entre les deux extrêmes se situent dans la zone de transition de l’ensemble, la limite. Au fur et à mesure que les valeurs s’éloignent de l’idéal ou du centre de l’ensemble, une valeur décroissante sur une échelle continue de 1 à 0 leur est attribuée. Au fur et à mesure que les valeurs attribuées diminuent, la possibilité que la valeur d’origine du phénomène appartienne à cet ensemble décroît.
La valeur d’appartenance floue de 0,5 correspond au point de croisement. Toute valeur floue supérieure à 0,5 implique que la valeur d’origine du phénomène peut appartenir à l’ensemble. Au fur et à mesure que les valeurs d’appartenance floue deviennent inférieures à 0,5, la possibilité que la valeur d’origine du phénomène appartienne à l’ensemble diminue ; les valeurs sont susceptibles de ne pas faire partie de l’ensemble.
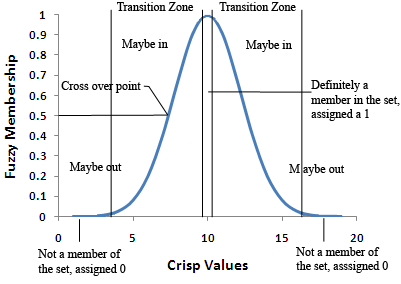
La largeur de la zone de transition dépend du phénomène modélisé, des connaissances au sujet du phénomène, de la définition de l’ensemble et de la précision des mesures. La modification des paramètres de la fonction d’appartenance floue peut définir les caractéristiques de la zone de transition. Dans l’image ci-dessous, la fonction Flou Gaussien est illustrée par trois courbes différentes dérivées de la modification des paramètres de la fonction.
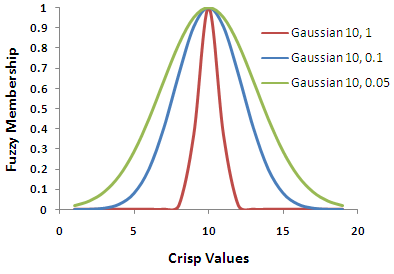
Les paramètres servent de modificateurs lors de la définition de l’ensemble. Les modificateurs caractérisent le chevauchement potentiel ou la zone intermédiaire entre les ensembles.
Le processus d’appartenance floue est effectué pour chaque critère de l’analyse de superposition.
Techniques de superposition floue
Les techniques de superposition floue permettent d’analyser les relations et l’interaction entre tous les ensembles selon les différents critères du modèle de superposition. Puisque que le processus d’appartenance floue repose sur le degré d’appartenance à un ensemble, les techniques de superposition décrivent l’interaction des imprécisions dans l’appartenance aux ensembles. Les techniques de superposition floue reposent sur la théorie des ensembles. La théorie des ensembles est une branche des mathématiques qui quantifie la relation d’appartenance de phénomènes à des ensembles spécifiques. Avec la superposition floue, un ensemble correspond généralement à une classe.
Les techniques de superposition d’ensembles flous disponibles sont les suivantes : ET flou, OU flou, Produit flou, Somme floue et Gamma flou. Chacune de ces techniques décrit la relation d’appartenance de la cellule aux ensembles en entrée. Par exemple, le type de superposition ET flou crée un raster en sortie dans lequel chaque valeur de cellule prend la valeur floue attribuée minimale pour chacun des ensembles auxquels la localisation de la cellule appartient. Si l’analyse de superposition est un modèle d’adéquation pour des logements et que chacun des multiples critères a été classé selon son appartenance floue aux ensembles adéquats, la fonction ET flou identifie la possibilité la plus faible d’appartenance de la cellule à l’un des ensembles adéquats selon les différents critères.
Le type OU flou renvoie la valeur maximale de l’intersection des ensembles. Ainsi, dans le modèle d’adéquation pour des logements, l’appartenance potentielle la plus élevée (la valeur d’adéquation la plus élevée) de chaque cellule est évaluée selon les différents critères.
Superposition binaire, pondérée et de logique floue
Dans de nombreuses descriptions de la logique floue pour l’analyse de superposition, elle est généralement comparée à l’analyse de superposition binaire. Dans le cadre de l’analyse de superposition binaire, le fait que chaque cellule appartienne ou non à une classe spécifiée est évalué selon chaque critère. Comme indiqué ci-dessus, il est souvent difficile de définir des limites de classe claires et d’attribuer de manière certaine des cellules à des classes spécifiques. Dans une analyse binaire, dans le cas d’un modèle d’adéquation pour des logements, chaque cellule est considérée comme adéquate (1) ou non (0) selon chaque critère. Dans le processus de superposition, les localisations qui prennent la valeur 1 pour tous les critères en entrée sont considérées comme des localisations potentiellement adéquates.
Les limitations de l’analyse de superposition binaire sont les suivantes :
- Si aucune localisation ne répond à tous les critères, aucune seconde meilleure option n’est identifiée.
- Il n’existe aucune pondération relative des localisations qui répondent aux critères.
- Les problèmes abordés précédemment concernant le processus de classification subsistent.
L’analyse de superposition pondérée tente de résoudre ces limitations. Au lieu de classer chaque cellule sur une échelle binaire de 1 ou 0, l’outil Superposition pondérée attribue à chaque cellule une valeur figurant sur une échelle continue définie, comme une échelle de 1 à 10, 10 étant la valeur préférée par rapport aux critères. L’échelle continue offre plus de gradations de classes, ce qui permet d’affiner davantage la représentation du phénomène. Pour chaque critère, une valeur de l’échelle de 1 à 10 est attribuée à chaque cellule. Les critères reclassés sont alors ajoutés les uns aux autres. Les localisations de cellule dotées des valeurs de somme les plus élevées sont alors préférées par rapport aux critères en entrée. Plus les critères favorables de chacune des entrées sont nombreux, mieux c’est.
La superposition floue et la superposition pondérée sont davantage similaires entre elles que par rapport à la superposition binaire. Elles reposent cependant sur des principes différents. La superposition floue est basée sur la théorie des ensembles, tandis que la superposition pondérée repose sur les combinaisons linéaires. Les deux techniques transforment les valeurs d’origine. Dans la superposition floue, la transformation définit la possibilité d’appartenance aux ensembles, tandis que la superposition pondérée fait intervenir une échelle de préférence. Étant donné que ces deux techniques sont uniques, les outils d’analyse selon les différents critères ne sont pas interchangeables.
Logique floue et processus général d’analyse de superposition
L’analyse de superposition avec logique floue suit les étapes générales de l’analyse de superposition, mais en mettant davantage d’accent sur certaines étapes, moins sur d’autres et en donnant une signification différente aux valeurs des nombres attribués par rapport aux autres approches d’analyse de superposition.
Les étapes générales de l’analyse de superposition sont les suivantes :
- Définir le problème.
- Décomposer le problème en sous-modèles.
- Identifier les couches significatives.
- Reclassifier ou transformer les données au sein d'une couche.
- Pondérer les couches en entrée.
- Ajouter ou combiner les couches.
- Analyser.
Comme pour toute analyse de superposition, les étapes 1 à 3 sont les mêmes pour l’analyse de logique floue. Étant donné que la logique floue repose sur des ensembles, la signification des valeurs reclassées (étape 4) et les techniques d’analyse pouvant être utilisées pour combiner les différents critères (étape 6) rendent la logique floue unique par rapport aux autres approches d’analyse de superposition.
Les sections suivantes traitent des différences de la logique floue lors des étapes 4 à 7.
Reclasser ou transformer les données dans une couche
Les données en entrée sont reclassées ou transformées sur une échelle de 0 à 1, identifiant la possibilité d’appartenance à un ensemble spécifié. Ce processus de reclassification ou d’appartenance floue est implémenté à l’aide de l’outil Appartenance floue. Une série de fonctions d’appartenance a été développée pour vous assister lors de ce processus de transformation. Les fonctions disponibles sont les suivantes : Flou Gaussien, Flou Grand, Flou linéaire, Flou MS Grand, Flou MS Petit, Flou Proche et Flou Petit. Chaque fonction d’appartenance transforme les données d’une manière spécifique pour capturer l’interaction du phénomène.
Pondérer les couches en entrée
Puisque la logique floue repose sur la théorie des ensembles et que vous cherchez à déterminer si une localisation particulière appartient à un ou plusieurs ensembles, la pondération n’a pas de sens. L’augmentation de la pondération d’un facteur par rapport à un autre facteur augmente la possibilité d’appartenance à un ensemble ou à une combinaison de plusieurs ensembles. La localisation appartient ou non à un ensemble (en tenant compte de tous les degrés intermédiaires). Dans une analyse de superposition floue, la pondération des critères n’est pas applicable.
Ajouter ou combiner les couches
Lors de l’étape d’ajout ou de combinaison, la logique floue explore l’interaction de la possibilité d’appartenance du phénomène à plusieurs ensembles, par opposition à la superposition pondérée et à la somme pondérée, qui reposent sur l’idée qu’un nombre plus important d’éléments favorables signifie un meilleur résultat.
Dans le cas de la superposition floue, des techniques spécifiques permettent d’étudier cette relation relative et de quantifier l’interaction. Les approches de combinaison sont les suivantes : ET flou, OU flou, Produit flou, Somme floue et Gamma flou. Chacune de ces approches repose sur la théorie des ensembles et est spécifique à l’analyse de superposition floue.
Analyser
Comme dans une analyse de superposition, il vous appartient d’analyser et d’interpréter les résultats. Cependant, en raison des différentes significations des valeurs reclassées et des techniques de superposition sous-jacentes dans chaque approche de superposition, il peut être nécessaire d’employer différents mécanismes pour mesurer la validité des résultats.
Vous avez un commentaire à formuler concernant cette rubrique ?