L’outil Superposition floue permet d’analyser la possibilité d’appartenance d’un phénomène à plusieurs ensembles dans une analyse de superposition tenant compte de multiples critères. L’outil Superposition floue identifie non seulement les ensembles auxquels le phénomène est susceptible d’appartenir, mais il analyse également les relations entre l’appartenance aux différents ensembles.
Le paramètre Type de superposition répertorie les méthodes disponibles pour combiner les données selon l’analyse de la théorie des ensembles. Chaque méthode permet d’explorer l’appartenance de chaque cellule aux différents critères en entrée. Les méthodes disponibles sont ET flou, OU flou, Produit flou, Somme floue et Gamma flou. Chaque approche traite un aspect différent de l’appartenance de chaque cellule aux différents critères en entrée.
ET flou
Le type de superposition ET flou renvoie la valeur minimale des ensembles auxquels appartient la localisation de la cellule. Cette technique est utile lorsque vous souhaitez identifier le plus petit dénominateur commun d’appartenance de tous les critères en entrée. Par exemple, dans un modèle d’adéquation pour des logements, vous pouvez sélectionner uniquement les localisations dont la possibilité d’adéquation à l’ensemble des critères est au moins égale à 0,5.
Le type ET flou utilise la fonction suivante lors de l’évaluation :
fuzzyAndValue = min(arg1, ..., argn)OU flou
Le type de superposition OU flou renvoie la valeur maximale des ensembles auxquels appartient la localisation de la cellule. Cette technique est utile lorsque vous souhaitez identifier les valeurs d’appartenance les plus élevées d’un des critères en entrée. Par exemple, dans un modèle d’adéquation pour des logements, vous pouvez identifier toutes les localisations dont au moins un des critères figure entièrement dans l’ensemble d’adéquation avec une valeur de 1.
Le type OU flou utilise la fonction suivante lors de l’évaluation :
fuzzyOrValue = max(arg1, ..., argn)Produit flou
Le type de superposition Produit flou multiplie, pour chaque cellule, chacune des valeurs floues de tous les critères en entrée. Le produit obtenu est inférieur à chacune des entrées, et lorsqu’un membre de plusieurs ensembles figure en entrée, la valeur peut être très petite. Il est difficile d’établir une corrélation entre le produit de tous les critères en entrée et la relation relative des valeurs. L’option Produit flou n’est pas souvent utilisée.
Le type Produit flou utilise la fonction suivante lors de l’évaluation :
fuzzyProductValue = product(arg1, ..., argn)Somme floue
Le type de superposition Somme floue ajoute les valeurs floues de chaque ensemble auquel appartient la localisation de la cellule. La somme obtenue est une fonction de combinaison linéaire croissante basée sur le nombre de critères entrés dans l’analyse.
La somme floue n’est pas une somme algébrique et ne doit pas être confondue avec l’approche d’addition utilisée dans les outils Superposition pondérée et Somme pondérée. Ces deux approches de superposition partent du principe que l’entrée la plus favorable est la meilleure. Ajouter toutes les valeurs d’appartenance à l’analyse Somme floue ne signifie pas nécessairement que la localisation est plus appropriée. L’option Somme floue n’est pas souvent utilisée.
Le type Somme floue utilise la fonction suivante lors de l’évaluation :
fuzzySumValue = 1 - product(1 - arg1, ..., 1 - argn)Gamma flou
Le type Gamma flou est un produit algébrique de la somme floue et du produit flou, tous deux élevés à la puissance de gamma. La fonction de généralisation est la suivante :
µ(x) = (FuzzySum)γ * (FuzzyProduct)1-γVoici la fonction spécifique utilisée par Gamma flou :
fuzzyGammaValue = pow(1 - ((1 - arg1) * (1 - arg2) * ...), Gamma) * pow(arg1 * arg2 * ..., 1 - Gamma)Si le gamma spécifié est de 1, la sortie est identique à celle du type Somme floue ; si le gamma est de 0, la sortie est identique à celle du type Produit flou. Les valeurs intermédiaires permettent de combiner des éléments entre ces deux extrêmes et d’obtenir un résultat potentiellement différent que ceux de OU flou ou ET flou. Gamma flou est un compromis entre l’effet croissant de Somme floue et l’effet décroissant de Produit flou. Le graphique suivant définit la relation de gamma avec les termes Somme floue et Produit flou :
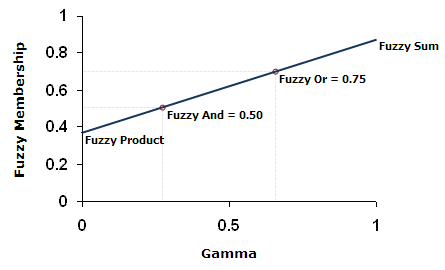
La superposition Gamma flou établit les relations entre plusieurs critères en entrée et ne renvoie pas simplement la valeur d’un seul ensemble d’appartenance, comme le font ET flou et OU flou.
Vous pouvez utiliser Gamma flou lorsque vous souhaitez utiliser des valeurs supérieures à Produit flou, mais inférieures à Somme floue.
Vous avez un commentaire à formuler concernant cette rubrique ?