Análisis de regresión—ArcGIS Insights

El análisis de regresión es una técnica de análisis que calcula la relación estimada entre una variable dependiente y una o varias variables explicativas. Con el análisis de regresión, es posible modelar la relación entre las variables elegidas, así como predecir valores basándose en el modelo.

Descripción general del análisis de regresión

El análisis de regresión utiliza un método de estimación elegido, una variable dependiente y una o varias variables explicativas para crear una ecuación que estima valores para la variable dependiente.

El modelo de regresión incluye salidas, tales como R² y valores P, para ofrecer información de en qué medida el modelo realiza estimaciones fiables de la variable dependiente.

También es posible utilizar gráficos, tales como matrices de gráficos de dispersión, histogramas y gráficos de puntos, en el análisis de regresión para analizar las relaciones y poner a prueba las suposiciones.

El análisis de regresión se puede usar para resolver los siguientes tipos de problemas:

Determinar qué variables explicativas están relacionadas con la variable dependiente.
Comprender la relación entre las variables dependientes y explicativas.
Predecir valores desconocidos de la variable dependiente.

Ejemplos

Un analista de una pequeña cadena minorista está estudiando el rendimiento de los distintos emplazamientos de sus tiendas. El analista desea saber por qué ciertos establecimientos presentan un volumen de ventas anormalmente bajo. El analista crea un modelo de regresión con variables explicativas, por ejemplo, la edad media y los ingresos del vecindario circundante, así como la distancia hasta los centros minoristas y el transporte público, como una forma de determinar qué variables influyen en las ventas.

Un analista de un departamento de educación está estudiando los efectos de los programas de desayuno en las escuelas. El analista crea un modelo de regresión de los resultados académicos obtenidos, tales como la tasa de graduaciones, mediante variables explicativas tales como tamaño del aula, ingresos de los hogares, presupuesto per cápita de los centros educativos y proporción de los alumnos que desayunan a diario. La ecuación del modelo se puede usar para determinar el efecto relativo de cada variable en los resultados académicos.

Un analista de una organización no gubernamental está estudiando las emisiones mundiales de gases de efecto invernadero. El analista crea un modelo de regresión de las emisiones más recientes de cada país mediante variables explicativas tales como producto interior bruto (PIB), población, producción eléctrica mediante combustibles fósiles y uso de vehículos. El modelo se puede usar a continuación para predecir las emisiones futuras de gases de efecto invernadero a partir de predicciones de valores de PIB y población.

Mínimos cuadrados ordinarios

El análisis de regresión de ArcGIS Insights se modela con el método de mínimos cuadrados ordinarios (OLS, por sus siglas en inglés).

El método de OLS es una forma de regresión lineal múltiple, lo que significa que la relación entre las variables dependientes y las variables independientes se debe modelar ajustando una ecuación lineal a los datos observados.

Los modelos OLS utilizan la siguiente ecuación:

y_i=β₀+β₁x₁+β₂x₂+...+β_nx_n+ε

donde:

y_i=el valor observado de la variable dependiente en el punto i
β₀=la intercepción y (valor constante)
β_n=el coeficiente de regresión o pendiente de la variable explicativa N en el punto i
x_n=el valor de la variable N en el punto i
ε=el error de la ecuación de regresión

Suposiciones

Cada método de regresión presenta distintas suposiciones que se deben cumplir para que la ecuación se considere fiable. Las suposiciones del método OLS se deben validar al crear un modelo de regresión.

Las siguientes suposiciones se deben evaluar y cumplir cuando se utiliza el método OLS:

El modelo debe ser lineal

La regresión OLS solo se puede usar para crear un modelo lineal. La linealidad entre la variable dependiente y las variables explicativas se puede evaluar mediante un gráfico de dispersión. Una matriz de gráficos de dispersión permite evaluar todas las variables, siempre y cuando no haya más de cinco variables en total.

Los datos se deben haber muestreado al azar

Los datos utilizados en el análisis de regresión se deben muestrear de forma que las muestras en sí no dependan de ningún factor externo. La aleatoriedad de las muestras se puede evaluar mediante los residuales del modelo de regresión. Los residuales, que son una salida del modelo de regresión, no deben presentar correlación al representarlos respecto de las variables explicativas en un gráfico de dispersión o una matriz de gráficos de dispersión.

Las variables explicativas no deben ser colineales

La colinealidad se refiere a una relación lineal entre las variables explicativas que crea redundancia en el modelo. En algunos casos, el modelo se puede crear con colinealidad. Sin embargo, si una de las variables colineales parece depender de otra, quizá desee plantearse eliminar esa variable del modelo. La colinealidad se puede evaluar mediante un gráfico de dispersión o una matriz de gráficos de dispersión de las variables explicativas.

Las variables explicativas deben presentar un error insignificante en la medición

La exactitud de todo modelo de regresión depende de sus datos de entrada. Si las variables explicativas presentan márgenes de error considerables, el modelo no se puede aceptar como exacto. Al realizar un análisis de regresión, es importante usar únicamente datasets provenientes de fuentes de confianza para garantizar que el error sea insignificante.

Los residuales presentan una suma esperada de cero

Los residuales son la diferencia entre los valores observados y los estimados de un análisis de regresión. Los valores observados que se encuentran por encima de la curva de regresión tendrán un valor residual positivo, mientras que los valores observados que se encuentran por debajo de la curva de regresión tendrán un valor residual negativo. La curva de regresión debe pasar por el centro de los puntos de datos; por tanto, la suma de los residuales debe ser cero. La suma de un campo se puede calcular en una tabla de resumen.

Los residuales presentan una varianza homogénea

La varianza debe ser la misma en todos los residuales. Esta suposición se puede evaluar mediante un gráfico de dispersión de los residuales (eje y) y los valores estimados (eje x). El gráfico de dispersión resultante debería aparecer como una banda horizontal de puntos representados al azar en el gráfico.

Los residuales están distribuidos de forma normal

Una distribución normal, también llamada como curva de campana, es una distribución que ocurre naturalmente: la frecuencia de un fenómeno es alta cerca del valor medio y se reduce gradualmente a medida que aumenta la distancia respecto del valor medio. La distribución normal se utiliza con frecuencia como hipótesis nula en el análisis estadístico. Los residuales deben presentar una distribución normal para mostrar que la línea de mejor ajuste está optimizada en el centro de los puntos de datos observados, sin sesgo hacia unos puntos o alejándose de otros. Esta suposición se puede evaluar creando un histograma a partir de los residuales. Es posible superponer la curva de distribución normal y las mediciones de sesgo y curtosis se reportan en el reverso de la tarjeta del histograma.

Los residuales adyacentes no deben presentar autocorrelación

Esta suposición se basa en la existencia de datos cronológicos. Si los datos son cronológicos, cada punto de datos debe ser independiente del punto de datos precedente o el posterior. Por tanto, es importante asegurarse de que sus datos cronológicos estén organizados en el orden correcto al realizar un análisis de regresión. Esta suposición se puede calcular mediante una prueba de Durbin-Watson.

La prueba de Durbin-Watson es una medida de la autocorrelación de los residuales de un modelo de regresión. La prueba de Durbin-Watson utiliza una escala de 0 a 4, en la que los valores 0 a 2 indican una autocorrelación positiva, el valor 2 indica ninguna autocorrelación y los valores 2 a 4 indican una autocorrelación negativa. Por tanto, se requieren valores cercanos a 2 para cumplir la suposición de que no exista autocorrelación en los residuales. En general, los valores comprendidos entre 1,5 y 2,5 se consideran aceptables, mientras que los valores menores que 1,5 o mayores que 2,5 indican que el modelo no se ajusta a la suposición de que no exista autocorrelación.

Validez del modelo

La precisión de una ecuación de regresión es una parte importante del análisis de regresión. Todos los modelos contendrán cierta cantidad de error, pero la comprensión de las estadísticas le ayudará a determinar si el modelo se puede usar para su análisis o si se requieren ajustes.

Existen dos técnicas para determinar la validez de un modelo de regresión: análisis exploratorio y análisis confirmatorio.

Análisis exploratorio

El análisis exploratorio es un método de comprensión de sus datos mediante una variedad de técnicas visuales y estadísticas. Durante el curso de su análisis exploratorio, evaluará las suposiciones de la regresión de OLS y comparará la eficacia de las distintas variables explicativas. El análisis exploratorio le permite comparar la eficacia y la precisión de distintos modelos, pero no determina si debería usar o rechazar su modelo. El análisis exploratorio debe realizarse antes del análisis confirmatorio en cada modelo de regresión y repetirse para hacer comparaciones entre modelos.

Se pueden usar los siguientes gráficos y estadísticas como parte del análisis exploratorio:

Gráfico de dispersión y matriz de gráficos de dispersión
Histograma y distribución normal
Ecuación de regresión y predicción de nuevas observaciones
Coeficiente de determinación, R² y R² ajustado
Error estándar residual
Gráfico de puntos

El análisis exploratorio debe comenzar mientras elije las variables explicativas y antes de crear un modelo de regresión. Dado que OLS es un método de regresión lineal, una de las principales suposiciones es que el modelo debe ser lineal. Se puede utilizar un gráfico de dispersión o una matriz de gráficos de dispersión para evaluar la linealidad entre la variable dependiente y las variables explicativas. Una matriz de gráficos de dispersión puede mostrar hasta cuatro variables explicativas junto con la variable dependiente, lo que la convierte en una importante herramienta para comparaciones a gran escala entre todas las variables. Un solo gráfico de dispersión muestra solamente dos variables: una dependiente y otra independiente o explicativa. Al visualizar un gráfico de dispersión de la variable dependiente y una sola variable explicativa, puede hacer una evaluación más precisa de la relación entre las variables. Puede evaluar la linealidad antes de crear un modelo de regresión para ayudar a determinar qué variables explicativas crearán un modelo aceptable.

Existen varios resultados estadísticos disponibles después de crear un modelo de regresión, incluida la ecuación de regresión, el valor R² y la prueba de Durbin-Watson. Una vez que haya creado un modelo de regresión, debería usar los resultados y los gráficos y tablas necesarios para evaluar el resto de suposiciones de la regresión de OLS. Si su modelo cumple las suposiciones, puede continuar con el resto del análisis exploratorio.

La ecuación de regresión proporciona información valiosa sobre la influencia de cada variable explicativa sobre los valores predichos, incluido el coeficiente de regresión de cada variable explicativa. Los valores de pendiente se pueden comparar para determinar la influencia relativa de cada variable explicativa sobre la variable dependiente; cuanto más alejado esté el valor de pendiente del cero (ya sea positivo o negativo), mayor será la influencia. La ecuación de regresión también se puede utilizar para predecir valores para la variable dependiente introduciendo valores para cada variable explicativa.

El coeficiente de determinación, simbolizado por R², mide hasta qué punto la ecuación de regresión modela los puntos de datos reales. El valor R² es un número entre 0 y 1, donde los valores más cercanos al 1 indican modelos más precisos. Un valor R² de 1 indica un modelo perfecto, lo cual es altamente improbable en situaciones reales dada la complejidad de las interacciones entre los distintos factores, además de las variables desconocidas. Por tanto, debe intentar crear un modelo de regresión que genere el máximo valor R² posible, pero siendo consciente de que es posible que el valor no se acerque a 1.

Al realizar el análisis de regresión, existe el riesgo de crear un modelo de regresión que presenta un valor R² aceptable al agregar variables explicativas que generan un mejor ajuste solo por azar. El valor R² ajustado, que también es un valor de entre 0 y 1, da cuenta de las variables explicativas adicionales, lo que reduce el papel del azar en el cálculo. Se debe usar un valor R² ajustado en los modelos que utilicen muchas variables explicativas, o al comparar modelos que presentan un número diferente de variables explicativas.

El error estándar residual mide la precisión con la que el modelo de regresión puede predecir valores con nuevos datos. Cuanto menores son los valores, más preciso es el modelo; por tanto, cuando se comparan varios modelos, el modelo con el menor valor será el modelo que minimice el error estándar residual.

Se pueden utilizar gráficos de puntos para analizar sus variables explicativas, a fin de encontrar patrones como clustering y valores atípicos, que podrían afectar a la precisión del modelo.

Análisis confirmatorio

En análisis confirmatorio es el proceso de evaluación de su modelo con una hipótesis nula. En el análisis de regresión, la hipótesis nula es que no existe relación entre la variable dependiente y las variables explicativas. Un modelo sin ninguna relación tendría valores de pendiente de 0. Si los elementos de su análisis confirmatorio son estadísticamente significativos, puede rechazar la hipótesis nula (es decir, una importancia estadística indica que existe una relación entre la variable dependiente y las explicativas).

Los siguientes resultados estadísticos se utilizan para determinar la importancia como parte del análisis confirmatorio:

Índice estadístico F y su valor P asociado
Índices estadísticos T y sus valores P asociados
Intervalos de confianza

El índice estadístico F es una estadística global devuelta de una prueba F, que indica la funcionalidad predictiva del modelo de regresión determinando si todos los coeficientes de regresión del modelo son significativamente diferentes a 0. La prueba F analiza la influencia combinada de las variables explicativas, en lugar de evaluar las variables explicativas individualmente. El índice estadístico F presenta un valor P asociado, que indica la probabilidad de que las relaciones de sus datos se estén produciendo por casualidad. Dado que los valores P se basan en probabilidades, los valores se indican en una escala de 0,0 a 1,0. Se requiere un valor P pequeño, normalmente 0,05 o menos, para determinar que las relaciones del modelo son reales (es decir, que no se producen por casualidad) y rechazar la hipótesis nula. En ese caso, la probabilidad de que las relaciones del modelo se produzcan por casualidad es de 0,05, o de 1 entre 20. Asimismo, la probabilidad de que las relaciones sean reales es de 0,95, o de 19 entre 20.

El índice estadístico T es una estadística local devuelta de una prueba T, que indica la funcionalidad predictiva de cada variable explicativa por separado. Al igual que la prueba F, la prueba T analiza si los coeficientes de regresión del modelo son significativamente diferentes a cero. Sin embargo, dado que la prueba T se realiza en cada variable explicativa, el modelo devolverá un valor estadístico T para cada variable explicativa, en lugar de uno por modelo. Cada índice estadístico T presenta un valor P asociado, que indica la importancia de la variable explicativa. Al igual que los valores P de la prueba F, el valor P de cada prueba T debería ser 0,05 o menos para rechazar la hipótesis nula. Si una variable explicativa presenta un valor P mayor que 0,05, la variable debería descartarse y habría que crear un nuevo modelo, aunque el valor P global fuera significativo.

Los intervalos de confianza muestran el coeficiente de regresión de cada variable explicativa y los intervalos de confianza de 90, 95 y 99 por ciento asociados. Por tanto, los intervalos de confianza se pueden utilizar junto con los valores P de las pruebas T para evaluar la hipótesis nula de variables explicativas individuales. Los coeficientes de regresión no deben ser iguales a 0 si va a rechazar la hipótesis nula y seguir usando el modelo. Por tanto, en cada variable explicativa, el coeficiente de regresión y los intervalos de confianza asociados no deben superponerse a 0. Si un intervalo de confianza del 99 o el 95 por ciento de una variable explicativa determinada se superpone a 0, la variable explicativa no ha rechazado la hipótesis nula. Incluir esta variable en su modelo podría afectar a la importancia general de su modelo. Si solamente el intervalo de confianza del 90 por ciento se superpone a 0, la variable explicativa podría incluirse en el modelo, siempre que el resto de estadísticas globales sean significativas. Lo ideal es que los intervalos de confianza de todas las variables explicativas estén alejados de 0.

Otros resultados

Otros resultados, como los valores estimados y los residuales, son importantes para evaluar las suposiciones de la regresión de OLS. En esta sección, obtendrá más información sobre cómo se calculan estos valores.

Valores estimados

Los valores estimados se calculan mediante la ecuación de regresión y los valores de cada variable explicativa. Lo ideal sería que los valores estimados fueran iguales a los valores observados (es decir, los valores reales de la variable dependiente).

Los valores estimados se utilizan con los valores observados para calcular residuales.

Valores residuales

Los valores residuales de un análisis de regresión son las diferencias entre los valores observados del dataset y los valores estimados calculados con la ecuación de regresión.

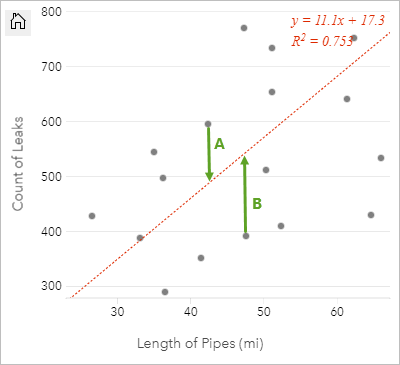
Los residuales A y B de la relación anterior se calcularía de la siguiente forma:

residuals_A = observed_A - estimated_A residuals_A = 595 - 487.62 residuals_A = 107.38

residuals_B = observed_B - estimated_B residuals_B = 392 - 527.27 residuals_B = -135.27

Los residuales se pueden usar para calcular el error en una ecuación de regresión, así como para evaluar distintas suposiciones.

¿Algún comentario sobre este tema?