La lógica difusa puede utilizarse como técnica de análisis de superposición para solucionar problemas en aplicaciones de análisis de superposición, como la selección de sitios y los modelos de adecuación.
El principio básico de la lógica difusa es la existencia de imprecisiones en el atributo y la geometría de los datos espaciales. La lógica difusa proporciona técnicas para abordar tipos de imprecisiones, pero, al pertenecer al análisis de superposición, se centra en las imprecisiones en los datos de atributos. Las dos áreas principales en las que se producen imprecisiones en los datos de atributos son la definición de las clases y la medición del fenómeno. Ambas causas de imprecisión, especialmente la definición de clases, pueden dar lugar a imprecisiones al asignar celdas a clases concretas.
La definición de las clases en una clasificación y la imprecisión al asignar fenómenos a clases pueden afectar a la toma de decisiones. Las herramientas de superposición difusa ayudan a los responsables de las decisiones a tomar decisiones sobre estas imprecisiones. La lógica difusa se centra en el modelado de imprecisiones de límites de clase.
Las herramientas Superposición ponderada y Suma ponderada se basan en conjuntos nítidos, en los que cada celda está o no en una clase. La lógica difusa se utiliza especialmente en situaciones en las que los límites entre clases no están claros. A diferencia de los conjuntos nítidos, la lógica difusa no tiene que ver con estar dentro o fuera de una clase, sino que define la probabilidad de que el fenómeno sea miembro de un conjunto (o clase). La lógica difusa se basa en la teoría de conjuntos; por tanto, lo que hace el usuario es definir posibilidades, en lugar de probabilidades.
Por ejemplo, en un modelo de adecuación de viviendas, si la pendiente es uno de los criterios de entrada, cada valor de pendiente se transformará o se le asignará un valor entre 0 y 1 relacionado con la posibilidad de que ese valor de pendiente pertenezca al conjunto de adecuación de ese edificio (o clase), de que sea adecuado. El valor 1 indica una certidumbre total de que el valor está en el conjunto y 0 indica que no está en el conjunto con total certidumbre. Todos los demás valores tienen un nivel de posibilidad y los valores más altos indican una mayor probabilidad de pertenencia. El proceso de transformación de los valores de entrada originales en la escala de posibilidad de pertenencia de 0 a 1 se denomina proceso de discretización. Se discretizarán todos los criterios del modelo, como la orientación, la distancia a carreteras y el tipo de uso del suelo. La herramienta Pertenencia difusa se utiliza para transformar los datos a la escala de posibilidad de 0 a 1.
Para determinar las ubicaciones que mejor satisfacen todos los criterios, es decir, que tienen mayor probabilidad de pertenecer a todos los conjuntos, se utiliza la herramienta Superposición difusa. Cuando se combinan varios criterios, la herramienta Superposición difusa explora la posibilidad de que la celda sea miembro de cada conjunto definido por los múltiples criterios. Por ejemplo, ¿cuál es la probabilidad de que una ubicación particular pertenezca a una adecuación favorable a la pendiente, la orientación y la distancia a las carreteras?
Por consiguiente, los dos pasos principales de la lógica difusa del análisis de superposición son la discretización, o proceso de pertenencia difusa, y el análisis de superposición difusa. Estos dos pasos guardan relación con los pasos de reclasificación/transformación y agregación/combinación, respectivamente, del proceso de superposición general.
Muchas veces no está claro que algo pertenezca o no a una clase, ya que es subjetivo. En el lenguaje humano, estas imprecisiones se definen mediante modificadores, como muy, levemente y de forma moderada. La lógica difusa realiza el análisis de superposición de manera parecida al pensamiento humano. Las cosas no son evidentes; los límites pueden ser difusos. La lógica difusa no analiza la incertidumbre en los datos, sino que examina la imprecisión en los límites de clase.
En las secciones siguientes se tratan los problemas con la clasificación de datos, el proceso de pertenencia difusa y la realización de análisis de superposición difusa. También se incluye una comparación de la lógica difusa con las técnicas de análisis de superposición binaria y ponderada y se explica cómo se integra la lógica difusa en el proceso de superposición general.
Clasificación de datos y lógica difusa
Para describir u ordenar fenómenos, debería tipificarlos de forma general en clases. La categoría de uso del suelo, el tipo de suelo, la ponderación de idoneidad, la clase de carreteras y el tipo de vegetación son ejemplos de clases. En el caso de los conjuntos nítidos, la pertenencia es binaria, y el fenómeno puede estar o no incluido en la clase. Los límites de clase están bien definidos. Sin embargo, debido a la impresión conceptual, la ambigüedad de las reglas de clasificación, la vaguedad y la ambivalencia, los límites entre clases no siempre están claros.
Por ejemplo, si el fenómeno que está examinando guarda relación con las diferentes alturas de las personas de un grupo, puede empezar agrupando a personas diferentes en clases en función de su altura. Puede empezar con tres clases: bajo, medio y alto. Tiene que establecer los límites de las clases. Por ejemplo, una persona baja puede ser cualquiera que mida 1,524 metros (5 pies) o menos, una persona alta puede medir 1,8288 metros (6 pies) o más y una persona de estatura media puede tener una altura de entre 1,6764 y 1,8288 metros (5 y 6 pies). Una persona que mida 1,8288 metros (6 pies) se incluirá en la clase alto. Si una persona mide 1,8034 metros (5' 11 pies), se clasificará como de estatura media. Aunque la diferencia de altura entre estas dos personas sea de 0,0254 metros (1 pulgada), pertenecerán a dos clases diferentes. Si otro miembro del grupo mide 1,5494 metros (5' 1) y el segundo mide 1,9812 metros (6' 6), se describirá la misma relación de diferencia. Debido a la inexactitud de las clasificaciones, no es posible captar todas las relaciones entre las alturas.
Para representar las relaciones de altura entre personas diferentes de forma más adecuada, pueden agregarse más clases. Por ejemplo, pueden agregarse dos clases más: bajo será 1,4732 metros (4' 10) o menos, la estatura media baja será de 1,4732 metros (4' 10) a 1,6256 metros (5' 4), la altura media será de 1,6256 metros (5' 4) a 1,778 metros (5' 10), la estatura media baja será de 1,778 metros (5' 10) a 1,9304 metros (6' 4), y alto será a partir de 1,9304 metros (6' 4). Al refinar las clases, la relación en la altura de las personas puede captarse con mayor precisión.
Esto puede mejorarse más agregando más clases. No importan cuántas clases se agreguen, porque la relación de altura entre persona sigue siendo generalizada. Existen algunos fenómenos que no pueden clasificarse en clases con una definición estricta. A veces resulta difícil agrupar los fenómenos del mundo real en clases separadas.
Como puede verse, la definición de los límites de clase es subjetiva y puede cambiar con la definición del fenómeno. En las clases de altura definidas antes, se presupone que las personas son adultas, y una mezcla de hombres y mujeres casi con toda probabilidad. Las definiciones de clase pueden tener que cambiar si el grupo está enteramente formado por mujeres. Los límites de clase podrían tener que cambiarse todavía más si el grupo estuviese formado por niños o incluyese niños.
La definición de clases y las características del fenómeno determinan la forma de representar el fenómeno que se está modelando. El error de medición complica más el problema de las clasificaciones. Si el proceso de medición de la altura de las personas contempla una precisión de más o menos 0,0254 metros (1 pulgada), la inexactitud puede cambiar la clase a la que se asigna un fenómeno.
La lógica difusa modela la imprecisión del proceso de clasificación. En la lógica difusa, las clases se definen como conjuntos. Existe un acuerdo con respecto a cuál es el valor ideal para pertenecer al conjunto; por ejemplo, el valor de pendiente ideal en un modelo de adecuación de viviendas. Conforme los valores se apartan del ideal, el nivel de claridad disminuye hasta un cierto punto en el que está claro que el valor no pertenece al conjunto (por ejemplo, está demasiado inclinado para construir).
Por ejemplo, en la aplicación de altura anterior, si se queda con las tres clases de altura (bajo, medio y alto), estas pueden superponerse en la lógica difusa.
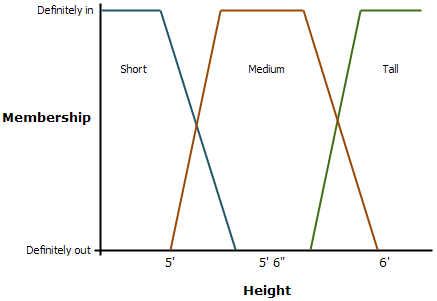
En la imagen anterior, la pertenencia plena a cada clase sería:
- Bajo: 1,524 metros (< 5 pies)
- Medio: 1,6129 metros (5' 3 1/2) a 1,7399 metros (5' 8 1/2)
- Alto: 1,8288 metros (> 6)
En el caso del conjunto (o clase) de estatura baja, cualquier persona que mida 1,524 metros (5 pies) o menos estará incluida en el conjunto de estatura baja y se le asignará el valor 1. Cualquier persona con estatura de más de 1,524 metros (5 pies) y menos de 1,6129 metros (5' 3 1/2) pertenecerá a los conjuntos (o clases) de estatura baja o media. Lo más probable es que las personas con altura entre 1,524 metros (5 pies) y 1,6129 metros (5' 3 1/2) estén en el conjunto de estatura baja. Las personas que midan más de 1,6193 metros (5' 1 3/4) y 1,6129 metros (5' 3 1/2) o menos posiblemente estarán en el conjunto de estatura baja, pero tendrán muchas posibilidades de formar parte del conjunto de estatura media.
En general, el proceso de discretización se implementa por medio de funciones predeterminadas mediante el uso de la herramienta Pertenencia difusa.
Pertenencia difusa
El proceso de discretización caracteriza la imprecisión de clases correspondientes a fenómenos que no tienen límites bien definidos.
La discretización convierte los valores originales del fenómeno en la posibilidad de que pertenezcan a un conjunto definido. El conjunto definido puede consistir en ser adecuado o estar dentro de una distancia favorable, o tener la posibilidad de encontrar un mineral determinado. Los valores originales del fenómeno se reclasifican en este continuo de pertenencia mediante funciones de pertenencia difusa predefinidas o de cualquier otra técnica de reclasificación.
En el proceso de discretización se establece la definición ideal de pertenencia al conjunto. A los valores del fenómeno que sean más importantes para el núcleo de la definición del conjunto se les asignará 1. Los valores que no formen parte del conjunto serán 0. Los valores situados entre los dos extremos se encuentran la zona de transición del conjunto: el límite. Conforme los valores se alejan del ideal o del centro del conjunto, se les asigna un valor decreciente en una escala continua de 1 a 0. A medida que los valores asignados disminuyen, el valor del fenómeno original tiene menos posibilidades de ser miembro de este conjunto.
El valor de discretización de 0,5 es el punto de cruce. Un valor difuso superior a 0,5 implica que el valor del fenómeno original puede pertenecer al conjunto. Cuando los valores de discretización descienden por debajo de 0,5, se reduce la probabilidad de que el valor del fenómeno original pertenezca al conjunto; los valores podrían no formar parte del conjunto.
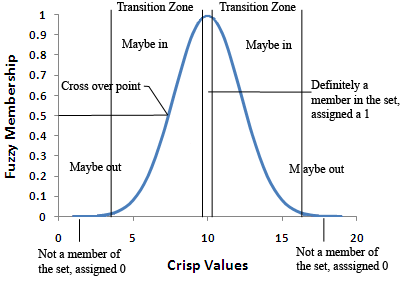
La anchura de la zona de transición depende del fenómeno que se va a modelar, lo que se sabe de este fenómeno, la definición del conjunto y la precisión de la medición. El cambio de los parámetros de la función de discretización puede definir las características de la zona de transición. En la imagen siguiente, la función Gaussiano difuso aparece con tres curvas diferentes derivadas del cambio de los parámetros de la función.
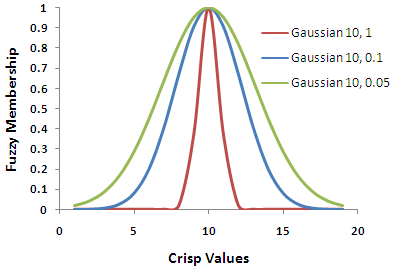
Los parámetros sirven como modificadores para definir el conjunto. Los modificadores caracterizan la superposición potencial o el espacio intermedio entre conjuntos.
El proceso de discretización tiene lugar con cada criterio del análisis de superposición.
Técnicas de superposición difusa
Para analizar la relación e interacción entre todos los conjuntos de múltiples criterios en el modelo de superposición se emplean técnicas de superposición difusa. Como el proceso de discretización se basa en el grado de pertenencia a un conjunto, las técnicas de superposición describen la interacción de las inexactitudes en la pertenencia de los conjuntos. Las técnicas de superposición difusa se basan en la teoría de conjuntos. La teoría de conjuntos es una disciplina matemática que cuantifica la relación de pertenencia de fenómenos a conjuntos específicos. Por lo general, en la superposición difusa, un conjunto corresponde a una clase.
Las técnicas de superposición de conjuntos difusa que están disponibles son Y difusa, O difusa, Multiplicación difusa, Suma difusa y Gamma difusa. Cada una de estas técnicas describe la relación de pertenencia de la celda con los conjuntos de entrada. Por ejemplo, el tipo de superposición Y difusa crea un ráster de salida en el que cada valor de celda recibe el valor difuso mínimo asignado a cada conjunto al que pertenece la ubicación de celda. Si el análisis de superposición es un modelo de adecuación de viviendas y cada uno de los múltiples criterios se ha discretizado en función de su pertenencia a conjuntos adecuados, Y difusa identifica la menor posibilidad de que la celda pertenezca a uno de los conjuntos adecuados según varios criterios.
El tipo O difusa devuelve el valor máximo de la intersección de los conjuntos. Es decir, en el modelo de adecuación de viviendas, la pertenencia con mayor potencial (el valor de adecuación más alto) correspondiente a cada celda se evaluará con respecto a varios criterios.
Superposición binaria, ponderada y de lógica difusa
En muchas descripciones de la lógica difusa correspondiente al análisis de superposición, suele compararse con el análisis de superposición binaria. En el análisis de superposición binaria, cada celda se evalúa con respecto a cada criterio para determinar si se encuentra en una clase determinada o no. Como se ha definido antes, en muchos casos, puede ser difícil definir unos límites de clase claros y asignar celdas a clases específicas de manera definitiva. En un análisis binario, en lo que respecta al modelo de adecuación de viviendas, cada celda se designa como adecuada (1) o no (0) con respecto a cada criterio. En el proceso de superposición, las ubicaciones a las que se asigna un 1 para todos los criterios de entrada se consideran potencialmente ubicaciones adecuadas.
Las limitaciones del método de análisis de superposición binaria incluyen lo siguiente:
- Si ninguna ubicación cumple todos los criterios, no se identifica ninguna segunda mejor opción.
- No existe ninguna ponderación relativa de las ubicaciones que cumpla los criterios.
- Los problemas mencionados antes sobre el proceso de clasificación.
El análisis de superposición ponderada intenta solucionar estas limitaciones. En lugar de clasificar cada celda en una escala binaria de 1 o 0, la herramienta Superposición ponderada asigna cada valor de celda en una escala continua definida, como una escala de 1 a 10, donde 10 es la alternativa que más se prefiere con respecto al criterio. La escala continua proporciona más gradaciones de clases, lo que permite refinar más la presentación del fenómeno. Cada celda se designa en la escala de 1 a 10 por cada criterio. Entonces, los criterios reclasificados se juntan. Las ubicaciones de celda con los valores sumados más altos son las más preferidas en relación con el criterio de entrada. Cuanto más favorable sea el criterio de cada entrada, mejor.
La superposición difusa y la superposición ponderada son más parecidas entre sí que la superposición binaria; sin embargo, las dos se basan en conceptos diferentes. La superposición difusa se basa en la teoría de conjuntos, mientras que la superposición ponderada se basa en combinaciones lineales. Ambas técnicas transforman los valores originales. En la superposición difusa, la transformación define la posibilidad de pertenecer a conjuntos, mientras que la superposición ponderada está en una escala de preferencia relativa. Como estas dos técnicas son exclusivas, las herramientas que realizan análisis según varios criterios no pueden intercambiarse.
Lógica difusa y el proceso de análisis de superposición general
El análisis de superposición de lógica difusa sigue los pasos del análisis de superposición general, pero con más énfasis en ciertos pasos, y menos en otros, y un significado diferente de los valores de los números asignados con respecto a otros métodos de análisis de superposición.
Los pasos generales del análisis de superposición son:
- Defina el problema.
- Divida el problema en submodelos.
- Determine las capas significativas.
- Reclasifique o transforme los datos que están dentro de una capa.
- Pese las capas de entrada.
- Agregue o combine las capas.
- Analice.
Como ocurre en todos los análisis de superposición, los pasos del 1 al 3 coinciden con los del análisis de lógica difusa. Como la lógica difusa se basa en conjuntos, el significado de los valores reclasificados (paso 4) y las técnicas de análisis que pueden utilizarse para combinar varios criterios (paso 6) hacen que la lógica difusa sea única con respecto a otros métodos de análisis de superposición.
En las secciones siguientes se explican las diferencias que presenta la lógica difusa en los pasos del 4 al 7.
Reclasificar o transformar los datos que están dentro de una capa
Los datos de entrada se reclasifican o transforman en una escala del 0 al 1, identificando la posibilidad de pertenecer a un conjunto determinado. Esta reclasificación o proceso de discretización se implementa por medio de la herramienta Pertenencia difusa. Se ha desarrollado una serie de funciones de pertenencia para facilitar este proceso de transformación. Las funciones disponibles son Gaussiano difuso, Grande difuso, Lineal difuso, MSGrande difuso, MSPequeño difuso, Cercano difuso y Pequeño difuso. Cada función de pertenencia transforma los datos de una forma concreta para captar la interacción del fenómeno.
Ponderar las capas de entrada
Como la lógica difusa se basa en la teoría de conjuntos y está determinando si una ubicación particular pertenece a uno o varios conjuntos, la ponderación carece de sentido. El aumento del peso de un factor con respecto a otro no puede aumentar la posibilidad de pertenecer a un conjunto o una combinación de varios conjuntos. La ubicación pertenece a un conjunto o no (junto con todos los grados intermedios). En el análisis de superposición difusa no procede ponderar los criterios.
Agregar o combinar las capas
En el paso de agregación o combinación, la lógica difusa examina la interacción de la posibilidad de que el fenómeno pertenezca a varios conjuntos, frente a la superposición ponderada y a la suma ponderada, que se basan en la idea de que más elementos favorables suponen un mejor resultado.
Para la superposición difusa, existen técnicas específicas para investigar esta relación relativa y para cuantificar la interacción. Los métodos de combinación son Y difusa, O difusa, Multiplicación difusa, Suma difusa y Gamma difusa. Cada uno de estos enfoques se basa en la teoría de conjuntos y es específica del análisis de superposición difusa.
Analizar
Como en el análisis de superposición, analizar e interpretar los resultados depende de usted. Sin embargo, debido a los diferentes significados de los valores reclasificados y a las técnicas de superposición subyacentes a cada método de superposición, podría requerirse el empleo de diferentes mecanismos para medir la validez de los resultados.