La herramienta Pertenencia difusa reclasifica o transforma los datos de entrada en una escala del 0 al 1 basada en la posibilidad de pertenecer a un conjunto específico. 0 se asigna a las ubicaciones que no pertenecen a un conjunto específico, 1 se asigna a los valores que sin duda pertenecen al conjunto y el rango entero de posibilidades entre 0 y 1 se asigna a algún nivel de posible pertenencia (cuanto más alto es el número, mayor es la posibilidad).
Los valores de entrada pueden transformarse de acuerdo con una serie de funciones y operadores disponibles en ArcGIS Spatial Analyst extension que pueden reclasificar los valores con arreglo a la escala de posibilidad de 0 a 1. Sin embargo, la herramienta Pertenencia difusa permite transformar los datos de entrada continuos con base en una serie de funciones específicas que son comunes al proceso de discretización. Por ejemplo, la función de pertenencia lineal difusa transforma los valores de entrada linealmente en la escala de 0 a 1, donde 0 se asigna al valor de entrada más bajo y 1 al valor de entrada más alto. Todos los valores intermedios reciben algún valor de pertenencia basado en una escala lineal, en la que los valores de entrada más altos tienen mayor posibilidad o están más próximos a 1.
En los scripts, cada una de estas funciones se implementa como clase de Python.
Como estas funciones de pertenencia son específicas de los datos de entrada continuos, cuando quiera utilizar los datos de categoría como entrada en el análisis de superposición difusa, necesita transformar los datos a la escala de posibilidad de pertenencia de 0 a 1 mediante cualquier cantidad de herramientas Spatial Analyst. Las dos herramientas que son más útiles en este proceso son Reclasificar y Dividir. La herramienta Reclasificar permite transformar los datos de categoría en una escala del 0 al 10 (no puede reclasificar los datos directamente en la escala del 0 al 1 con la herramienta) y luego dividir los datos transformados resultantes entre 10 para obtener la escala del 0 al 1.
Las funciones de pertenencia varían en función de su aplicación y ecuación. Su elección depende de cuál es la función que mejor representa la transformación de los datos según el fenómeno que se está modelando. Puede refinar aún más las características de cada función de pertenencia a través de una serie de parámetros de entrada.
A continuación se incluye una lista de las funciones de pertenencia difusa y cuál es su uso óptimo. Con cada función se incluye un gráfico. En el eje x están los valores de entrada (que aparecen como valores de nitidez en los gráficos) y en el eje y se encuentran los valores de pertenencia difusa transformados.
Tipos de pertenencia difusa
A continuación se explica cada una de las siete funciones de pertenencia difusa.
Gaussiano difuso
La función Gaussiano difuso transforma los valores originales en una distribución normal. El punto medio de la distribución normal especifica la definición ideal del conjunto, designado como 1, y la pertenencia del resto de valores de entrada disminuye a medida que se alejan del punto medio en dirección positiva y negativa. Los valores de entrada decrecen en cuanto a pertenencia a partir del punto medio hasta llegar a un punto en el que los valores se alejan demasiado de la definición ideal, definitivamente no están en el conjunto y se les asignan ceros.
El cambio del parámetro de propagación modifica el ancho y el carácter de la zona de transición.
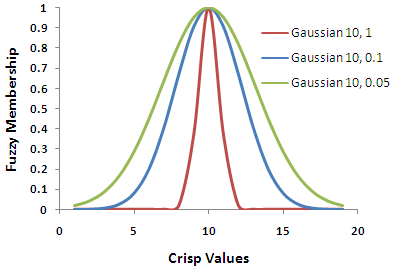
La función Gaussiano es útil cuando la pertenencia está cerca de un valor específico. Por ejemplo, en un modelo de adecuación de viviendas, la orientación sur es la orientación ideal de construcción para la captación solar, y las orientaciones menores o mayores que 180 son menos favorables o tienen menos probabilidad de pertenecer al conjunto de adecuación ideal.
Grande difusa
La función de transformación Grande difusa se utiliza cuando es más probable que los valores de entrada grandes pertenezcan al conjunto. El punto medio definido identifica el punto de transición (al que se asigna una pertenencia de 0,5); los valores mayores que el punto medio tienen más posibilidad de pertenecer al conjunto y los valores por debajo del punto medio tienen una pertenencia decreciente. El parámetro de propagación define la forma y el carácter de la zona de transición.
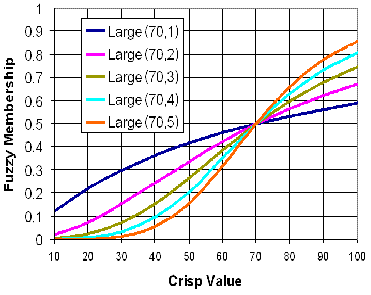
En el modelo de adecuación de viviendas se puede utilizar la función Grande difusa para transformar los valores de distancia desde una capa de vertedero. Cuanto más lejos están las ubicaciones del vertedero, más probabilidad existe de que pertenezcan al conjunto de adecuación favorable.
Lineal difusa
La función de transformación Lineal difusa aplica una función lineal entre los valores mínimos y máximos especificados por el usuario. Se asignará 0 a cualquier valor por debajo del mínimo (no miembro) y 1 a cualquier valor por encima del máximo (miembro). La línea azul de la imagen siguiente representa una transformación lineal con inclinación positiva, mínimo de 30 y máximo de 80. Se asignará 0 a cualquier valor por debajo de 30 y 1 a cualquier valor por encima de 80.
Si el mínimo es mayor que el máximo, se establece una relación lineal negativa (una pendiente negativa). La línea roja de la imagen siguiente representa una transformación lineal con inclinación negativa. Se asignará 1 a cualquier valor menor que 30 y 0 a cualquier valor mayor que 80.
El punto en que la inclinación de la línea aumenta o desciende define la zona de transición (entre 30 y 80 en la imagen siguiente).
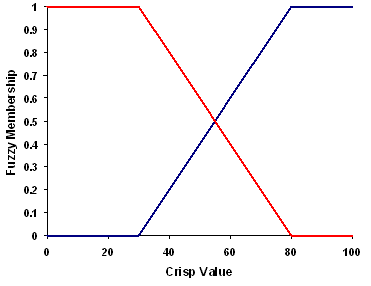
La función de transformación Lineal difusa del ejemplo de adecuación de viviendas puede utilizarse para el criterio de distancia de zonas reactivas (transformación lineal negativa). Cualquier ubicación que esté a 500 metros de un área recreativa podría estar en el conjunto de adecuación favorable, mientras que entre 500 y 10.000 metros se reduce linealmente la posibilidad de estar en el conjunto de adecuación, y cualquier ubicación que quede a más de 10.000 metros estaría demasiado lejos del área recreativa como para formar parte del conjunto favorable y se le asignaría un 0.
MSLarge difusa
La función de transformación MSLarge difusa es similar a la función Grande difusa, excepto que la definición de la función está basada en una media y una desviación estándar determinadas. Por lo general, la diferencia entre las dos funciones es que la función MSLarge difusa puede ser más adecuada cuando es más probable que los valores muy grandes pertenezcan al conjunto.

Los resultados pueden ser similares a la función Grande dependiendo del valor medio y la desviación estándar definidos.
MSSmall difusa
La función de transformación MSSmall difusa es similar a la función Pequeña difusa, excepto que la definición de la función está basada en una media y una desviación estándar determinadas. Por lo general, la diferencia entre las dos funciones es que la función MSSmall difusa puede ser más adecuada cuando es más probable que los valores muy pequeños pertenezcan al conjunto.
Los resultados pueden ser similares a la función Pequeño, según cómo se definan los multiplicadores del valor medio y la desviación estándar.
Cercano difuso
La función de transformación Cercano difuso es de la máxima utilidad cuando la pertenencia se aproxima a un valor específico. La función está definida por un punto medio que determina el centro del conjunto, que identifica la pertenencia y que, por tanto, se le asigna un 1. Al apartarse del punto medio en ambas direcciones (positiva y negativa), la pertenencia se reduce hasta 0, que implica no pertenencia. La propagación define el ancho y el carácter de la zona de transición.
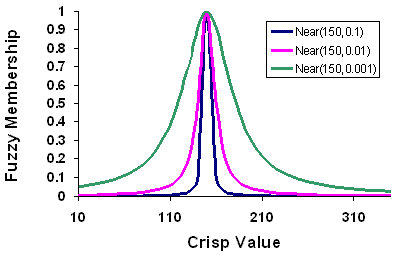
Cercano difuso y Gaussiano difuso pueden ser similares según los parámetros especificados. Por lo general, la función Cercano difuso decrece más rápidamente con una anchura más estrecha que la función Gaussiano difuso y, por consiguiente, se utiliza cuando es más probable que los valores muy próximos al punto medio pertenezcan al conjunto.
Pequeña difusa
La función de transformación Pequeña difusa se utiliza cuando es más probable que los valores de entrada pequeños pertenezcan al conjunto. El punto medio definido identifica el punto de transición (al que se asigna una pertenencia de 0,5); los valores mayores que el punto medio tienen menos posibilidad de pertenecer al conjunto y los valores por debajo del punto medio tienen más posibilidad de pertenencia. El parámetro de propagación define la forma y el carácter de la zona de transición.
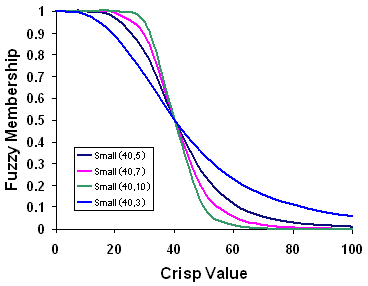
La función de transformación Pequeña difusa del ejemplo de adecuación de viviendas puede utilizarse para el criterio de distancia de electricidad. A medida que aumenta la distancia del tendido eléctrico, es más caro acceder a la electricidad y, por tanto, menos probable que las ubicaciones pertenezcan al conjunto de adecuación favorable. El criterio de acceso a la electricidad no se modela como una transformación lineal para tener en cuenta la necesidad de transformadores eléctricos conforme aumenta la distancia.