Sobald die angepasste geradlinige Entfernung berechnet wurde, können Sie mithilfe des vertikalen Faktors die Geschwindigkeit steuern, mit der die Entfernung zurückgelegt wird. Mithilfe der Kostenoberfläche, der Eigenschaften des Reisenden und des horizontalen Faktors können Sie die Geschwindigkeit ebenfalls steuern.
Der vertikale Faktor berücksichtigt die Anstrengung, die mit der Bewegung durch die Neigungen in der Landschaft verbunden ist. Diese Anstrengung wirkt sich darauf aus, wie die Entfernung zurückgelegt wird. Bergauf zu gehen ist u. U. anstrengender, während bergab zu gehen weniger Anstrengung erfordert, und das Überqueren von Neigungen liegt irgendwo dazwischen. Indem die angepasste geradlinige Entfernung im Hinblick auf diese Anstrengung geändert wird, lässt sich die Geschwindigkeit, mit der der Reisende die Entfernung zurücklegt, leichter erfassen.
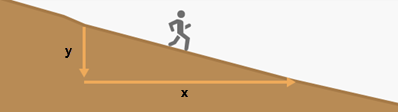
Der vertikale Faktor, der für die Anstrengung steht, die mit der Bewältigung von Neigungen verbunden ist, ist nicht mit der Oberflächenentfernung zu verwechseln, bei der es sich um eine Anpassung an die geradlinige Entfernung um die tatsächliche Entfernung handelt, die der Reisende auf seinem Weg bergauf und bergab durch die Landschaft zurücklegt.
Die Neigung ist oftmals relevant für die Kostenentfernungsanalyse. Es liegt nahe, dass es mehr Anstrengung kostet, starke Neigungen zu bewältigen als flachere Neigungen. In der Regel wird mithilfe des Werkzeugs Oberflächenparameter ein Neigungs-Raster generiert; zuweilen wird dieses Neigungs-Raster jedoch fehlerhaft in die Kostenoberfläche eingegeben.
Mit der Option Neigung im Werkzeug Oberflächenparameter wird die Änderungsrate der Höhe für jede Zelle des digitalen Höhenmodells (DEM) berechnet. Dies ist die erste Ableitung eines DEM. Wie oben bereits erläutert ist es jedoch von Bedeutung, wie die Neigung auf dem Weg durch eine Zelle bewältigt wird. Möglicherweise meidet der Reisende eine Zelle, der eine starke Neigung in einer Kostenoberfläche zugewiesen ist. Dies kann effektiv sein, wenn sich der Reisende auf seinem Weg durch die Zelle auf der Neigung nach oben bewegt. Bewegt sich der Reisende auf seinem Weg durch die Zelle jedoch abwärts oder überquert er die Neigung, bevorzugt er die Zelle möglicherweise für seine Reise.
Sie können die mit der Bewältigung der Neigung verbundene Anstrengung im vertikalen Faktor mithilfe des Höhen-Rasters berücksichtigen. Beziehen Sie das Neigungs-Raster nicht in die Kostenoberfläche ein, wenn die Richtung, in der die Neigung bewältigt wird, von Bedeutung ist.
Die Richtung, in der Neigungen im vertikalen Faktor berechnet werden, lässt sich außerdem durch den Parameter Reiserichtung für die Quelleneigenschaften verändern. Das heißt, dass sich die Richtung, in der der Reisende die Zelle betritt, und infolgedessen die Art und Weise, in der die Neigung überwunden wird, ändern, je nachdem, ob er sich zu einer Quelle hin oder von ihr weg bewegt.
Die Einbindung des vertikalen Faktors (VF) ist ein Multiplikator-Modifikator für die Berechnung der angepassten geradlinigen Entfernung.
Beispiele zur Verwendung des vertikalen Faktors
Der vertikale Faktor kann in verschiedenen Szenarien verwendet werden, wie z. B. in den folgenden:
- Suchen Sie einen neuen Wanderweg zwischen zwei Campingplätzen, der zwar länger, dafür aber leichter zu begehen ist, als wenn direkt über die kürzeste Route zwischen ihnen bergauf gewandert würde.
- Untersuchen Sie die Auswirkungen, die das im Winter auf den Straßen verteilte Salz auf den Zustand der Vegetation in der Umgebung hat. Die Vegetation unterhalb der Straße wird stärker durch das abfließende Wasser beeinträchtigt.
- Ermitteln Sie die Bewegungen eines Meeresbewohners, die sich nach der Veränderung des Salzgehaltes richten.
Einbeziehen eines vertikalen Faktors
Die Entfernungsanalyse kann konzeptionell in die folgenden verwandten Funktionsbereiche unterteilt werden:
- Berechnen Sie die geradlinige Entfernung, und passen Sie die Berechnungen optional mit einem Barriere- oder Oberflächen-Raster an.
- Nachdem die geradlinige Entfernung berechnet wurde, ermitteln Sie optional die Geschwindigkeit, mit der die Entfernung zurückgelegt wird, und zwar durch eine Kostenoberfläche, die Quelleneigenschaften, einen vertikalen Faktor und einen horizontalen Faktor. Erstellen Sie das akkumulative Entfernungs-Raster.
- Verbinden Sie Regionen über die resultierende akkumulative Entfernungsoberfläche mithilfe eines optimalen Netzwerks, spezifischer Pfade oder eines Korridors miteinander.
Ermitteln Sie aus dem zweiten Funktionsbereich durch einen vertikalen Faktor, wie unten dargestellt, die Geschwindigkeit, mit der die Entfernung zurückgelegt wird. In dem Szenario sind vier forstwirtschaftliche Ranger-Stationen (violette Punkte) und einige Flüsse (blaue Linien) enthalten.
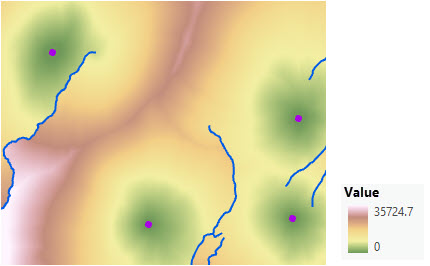
Um die Anstrengung der Ranger bei der Überwindung der Neigungen einzubeziehen, wird ein vertikaler Faktor angegeben. Die Höhenoberfläche dient als vertikales Raster.
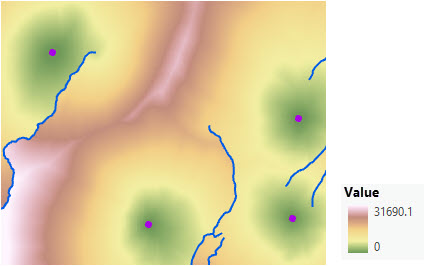
Erstellen eines Entfernungs-Rasters mithilfe eines vertikalen Faktors
Führen Sie die folgenden Schritte aus, um eine Entfernungskarte zu erstellen, die einen vertikalen Faktor enthält:
- Öffnen Sie das Werkzeug Entfernungsakkumulation.
- Geben Sie eine Quelle für den Parameter Eingabe-Raster oder Feature-Quellen-Daten an.
- Geben Sie dem Ausgabe-Entfernungs-Akkumulations-Raster einen Namen.
- Blenden Sie die Kategorie Kosten im Verhältnis zur vertikalen Bewegung ein.
- Stellen Sie ein Raster mit einem vertikalen Faktor für den Parameter Eingabe-Vertikal-Raster bereit.
Mithilfe dieser Eingabe wird die Neigung berechnet, die bei der Bewegung zwischen Zellen überwunden wird. In der Regel muss ein Höhen-Raster angegeben werden.
Der Parameter Vertikaler Faktor wird angezeigt.
- Geben Sie die Einstellungen für den Parameter Vertikaler Faktor an.
Mit diesem Parameter wird der Multiplikator angegeben, der auf die Kosten angewendet wird, um die Anstrengung auszugleichen, die mit der Bewegung über die zu überwindenden Neigungen verbunden ist.
- Klicken Sie auf Ausführen.
Der vertikale Faktor wirkt sich auf die Geschwindigkeit aus, mit der die Entfernung zurückgelegt wird.
Um die Geschwindigkeit zu ändern, mit der die Entfernung zurückgelegt wird, und um der Anstrengung des Reisenden bei der Überwindung der Neigungen Rechnung zu tragen, führt das Werkzeug intern zwei Aktionen aus.
- Berechnen Sie, wie die Neigung auf dem Weg von einer Zelle zur nächsten überwunden wird. Dies wird als vertikaler relativer Bewegungswinkel (Vertikal Relative moving Angle, VRMA) bezeichnet.
- Bestimmen Sie, wie der VRMA die Geschwindigkeit ändert, mit der die Entfernung zurückgelegt wird.
Berechnen des VRMA
Der VRMA ist der Neigungswinkel ausgehend von der Verarbeitungszelle (der Ausgangszelle) zu der Zelle, in die sich der Reisende bewegt (der Zielzelle). Die Entfernung wird für die Zielzelle berechnet. Die Höhen, von denen aus die Neigungen berechnet werden, werden durch das Eingabe-Raster für den vertikalen Faktor definiert.
Die Neigung wird mit dem Satz des Pythagoras berechnet. Die Basis des Dreiecks, das zur Bestimmung der Neigung erforderlich ist, wird von der angepassten geradlinigen Entfernung abgeleitet. Die Höhe wird festgelegt, indem man den Wert der Startzelle vom Wert der Zielzelle subtrahiert. Der resultierende Winkel ist der VRMA.
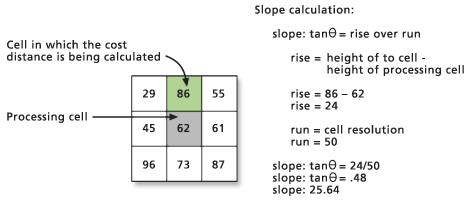
Der VRMA wird in Grad angegeben. Der Wertebereich für den VRMA ist –90 bis +90 Grad und berücksichtigt sowohl positive als auch negative Neigungen.
Bestimmen des VF-Multiplikators
Der VRMA-Wert wird dann auf dem angegebenen Diagramm für den vertikalen Faktor geplottet, um den Multiplikator des vertikalen Faktors zu erhalten, der in den Berechnungen verwendet wird, mit denen die mit dem Erreichen der Zielzelle verbundenen Kosten ermittelt werden. Der Entfernungswert für die Bewegung durch die Zelle wird mit dem so bestimmten vertikalen Faktor multipliziert. Je größer der vertikale Faktor, je schwieriger die Bewegung. Ein VF von über 1 erhöht die Kosten der zurückgelegten Entfernung. Bei einem VF von unter 1 und über 0 kann der Reisende die Entfernungen schneller zurücklegen.
Als Beispiel zeigt der folgende Graph die Beziehung zwischen dem VF und dem VRMA als lineare VF-Funktion:
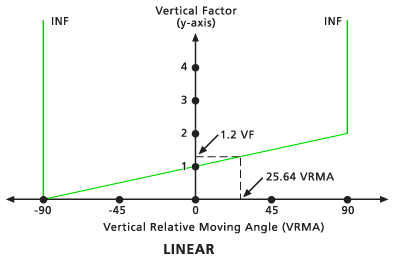
Die Funktionen des vertikalen Faktors, mit denen Sie die Interaktion zwischen dem Reisenden und den Neigungen, die er zurücklegt, erfassen, sind Binär, Linear, Invers linear, Symmetrisch linear, Symmetrisch invers linear, Cos, Sec, Cos-Sec und Sec-Cos. Einzelheiten zu den einzelnen Funktionen finden Sie weiter unten im Abschnitt Zusätzliche Informationen.
Hinweis:
Der vertikale Faktor ist ein Multiplikator. Gehen Sie vorsichtig vor, wenn Sie beim Kombinieren des vertikalen Faktors mit einer Kostenoberfläche, Quelleneigenschaften oder einem horizontalen Faktor die Einheiten angeben. Bei Eingabe einer Kostenoberfläche sollte der vertikale Faktor im Allgemeinen ein Multiplikatorausgleich für die Einheiten der Kostenoberflächenrate sein. Wenn Zeit die Einheit für die Kostenoberflächenrate ist, sollte mit dem vertikalen Faktor die Zeit modifiziert werden. Die Einheiten für die Rate können nur durch einen dieser Faktoren definiert werden. Die anderen Faktoren haben keine Einheiten, und ihre Werte sind Multiplikator-Modifikatoren der angegebenen Einheiten.
Beispielanwendungen für die Verwendung eines vertikalen Faktors
Im Folgenden sind die Beispielanwendungen beschrieben, die einen vertikalen Faktor verwenden.
Erstellen eines Neigungspuffers zum besseren Verständnis der Auswirkung des Streusalzes im Winter auf die Vegetation
Sie möchten Flächen mit einer Neigung identifizieren, die maximal 50 Meter von einer Straße entfernt sind, da diese Flächen im Winter u. U. von abfließendem Salzwasser beeinträchtigt werden. Sie möchten die Entfernung entlang der Oberfläche des Terrains messen. Mit der Einstellung Binär des vertikalen Faktors können Sie verhindern, dass das Werkzeug Entfernungsakkumulation Zellen identifiziert, die höher liegen als Straßenzellen. Beispiele der daraus resultierenden Neigungspuffer finden Sie unten.
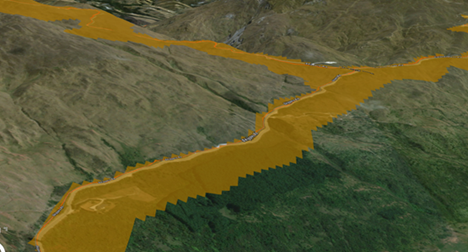
Zum Vergleich wird ein anderer Abschnitt der Straße herangezogen, um den Unterschied zwischen den Puffern für die geradlinige Entfernung und den Puffern nur für die Abwärtsneigung darzustellen. Diesen sehen Sie unten.
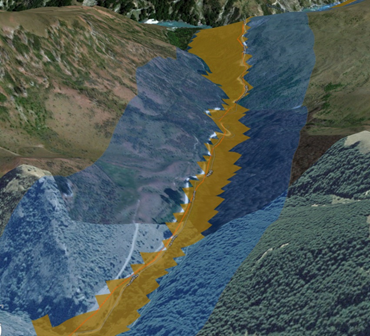
Führen Sie die folgenden Schritte aus, um einen Neigungspuffer zu erstellen:
- Öffnen Sie das Werkzeug Entfernungsakkumulation.
- Geben Sie die Straßen in den Parameter Eingabe-Raster oder Feature-Quellen-Daten ein.
- Geben Sie dem Wert Ausgabe-Entfernungs-Akkumulations-Raster einen Namen.
- Blenden Sie die Kategorie Kosten im Verhältnis zur vertikalen Bewegung ein.
- Geben Sie ein Höhen-Raster im Parameter Eingabe-Vertikal-Raster an.
- Legen Sie Binär für den Parameter Vertikaler Faktor fest.
- Blenden Sie die Kategorie Quelleneigenschaften ein.
- Legen Sie den Entfernungsparameter Maximale Akkumulation auf 50 Meter fest.
- Klicken Sie auf Ausführen.
Wanderfunktion nach Tobler
Sie möchten berechnen, wie lange eine Wanderung durch die Landschaft dauert, während Sie gleichzeitig die Gehgeschwindigkeit basierend auf der Neigung anpassen, die in Reiserichtung zu überwinden ist. Die Wanderfunktion nach Tobler (1993) ist ein empirisches Modell, mit dem diese Anpassung durchgeführt wird. In dem Modell wird von einer Wandergeschwindigkeit von 6 km/h ausgegangen, die erreicht wird, wenn der Weg leicht abwärts (ca. –3 Grad) verläuft.

Dabei wird S bezogen auf die Neigung d (angegeben in Grad) definiert, sodass S = tan(d π/180)
Die Geschwindigkeitsfunktion W sieht wie folgt aus:
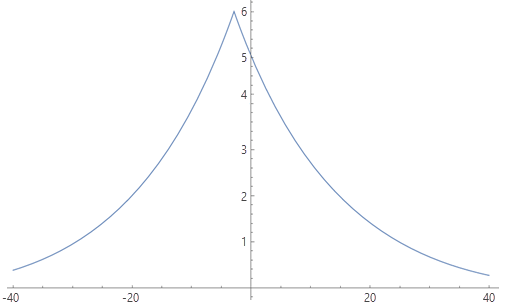
Sie möchten wissen, wie lange es dauert, eine bestimmte Entfernung (eine Zelle) zurückzulegen, und nicht, wie weit Sie in einer bestimmten Zeit kommen, sodass Sie mit dem Reziprok der Geschwindigkeit arbeiten müssen, dem Tempo. Das Tempo wird in Stunden pro Meter ausgedrückt und nicht in Kilometern pro Stunde:
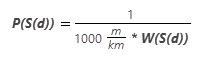
Die Tempofunktion sieht wie folgt aus:
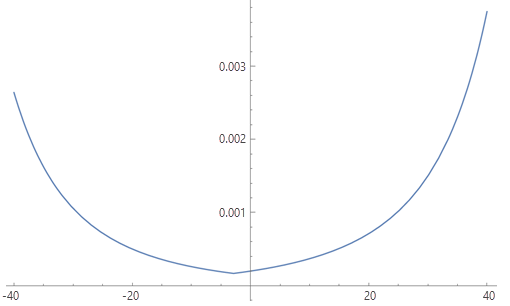
Ermitteln Sie den Wert P(S) für einen Wertebereich von d, und speichern Sie ihn in einer Tabelle (unten im Abschnitt "Tabelle" dargestellt). Anschließend kann die Tabelle mit der Funktion Tabelle für den vertikalen Faktor verwendet werden, um die Kosten pro Zelle unter Berücksichtigung der Bewegungsrichtung durch eine Zelle anzugeben. Die Kosten (in Zeit), die mit der Bewegung durch eine Zelle in einer bestimmten Richtung und der Überwindung einer Neigung d verbunden sind, sind P(S(d)) * Zellengröße (in Metern).
Wenn Sie in derselben Analyse neben der Wanderfunktion nach Tobler (Tempo) eine richtungsunabhängige Eingabekosten-Reibungsoberfläche verwenden möchten, achten Sie auf die Einheiten für die Eingabe der Reibungskosten. In jeder Zelle multipliziert das Werkzeug Entfernungsakkumulation P(S) * (Eingabekosten in der Zelle), sodass nicht beide Werte in Tempoeinheiten angegeben werden können. Sie können entweder die Tempofunktion nach Tobler so ändern, dass sie lediglich eine Gewichtung ist (ersetzen Sie die 6 durch eine 1, wenn Sie der Meinung sind, dass dies empirisch gerechtfertigt ist), oder in Ihrer Kosteneingabe Gewichtungen ohne Einheiten verwenden.
Weitere Informationen
Die folgenden Abschnitte enthalten zusätzliche Informationen zu vertikalen Faktoren.
Vertikale Faktoren
Um die Funktion für den vertikalen Faktor zu definieren, können Sie eine Funktion aus einer Liste von bereitgestellten Graphen auswählen, oder eine benutzerdefinierte Funktion mithilfe einer ASCII-Datei erstellen. Die folgenden Funktionen für den vertikalen Faktor stehen im Werkzeug Entfernungsakkumulation zur Verfügung:
Optionen, Modifikatoren und Standardwerte für den vertikalen Faktor
| Funktion | Null-Faktor | Tiefer Schnittwinkel | Hoher Schnittwinkel | Neigung | Potenz | Cos-Potenz | Sec-Potenz |
|---|---|---|---|---|---|---|---|
| Binär | 1 | -30 | 30 | N.z. | N.z. | N.z. | N.z. |
| Linear | 1 | -90 | 90 | 1.111E-02 | N.z. | N.z. | N.z. |
| Invers Linear | 1 | -45 | 45 | -2.222E-02 | N.z. | N.z. | N.z. |
| Symmetrisch Linear | 1 | -90 | 90 | 1.111E-02 | N.z. | N.z. | N.z. |
| Symmetrisch Invers Linear | 1 | -45 | 45 | -2.222E-02 | N.z. | N.z. | N.z. |
| Cos | N.z. | -90 | 90 | N.z. | 1 | N.z. | N.z. |
| Sec | N.z. | -90 | 90 | N.z. | 1 | N.z. | N.z. |
| Cos – Sec | N.z. | -90 | 90 | N.z. | N.z. | 1 | 1 |
| Sec – Cos | N.z. | -90 | 90 | N.z. | N.z. | 1 | 1 |
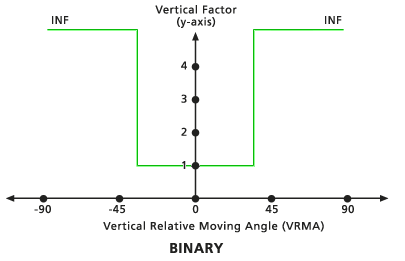
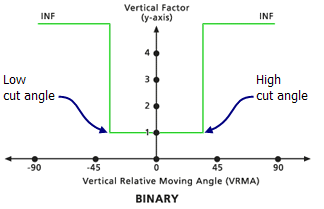
Binär
Wenn der VRMA größer als der niedrige Schnittwinkel und kleiner als der hohe Schnittwinkel ist, wird der VF zum Bewegen zwischen zwei Zellen auf den dem Null-Faktor zugewiesenen Wert festgelegt. Wenn der VRMA größer als der Schnittwinkel ist, wird der VF auf unendlich festgelegt. Der Standard-Schnittwinkel ist 30 Grad, sofern keiner festgelegt ist.
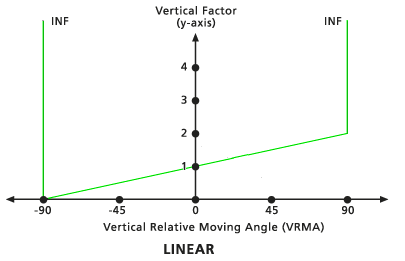
Linear
Die VFs werden von einer geraden Linie im VRMA-VF-Koordinatensystem bestimmt. Die Linie schneidet die Y-Achse entsprechend dem VF-Faktor am Null-Faktor-Wert. Die Neigung der Linie kann mit dem Modifizierer Neigung angegeben werden. Wenn keine Neigung identifiziert wird, beträgt der Standard 1/90 (angegeben als 0,01111). Der niedrige Standard-Schnittwinkel beträgt -90 Grad, der hohe Standard-Schnittwinkel beträgt 90 Grad.
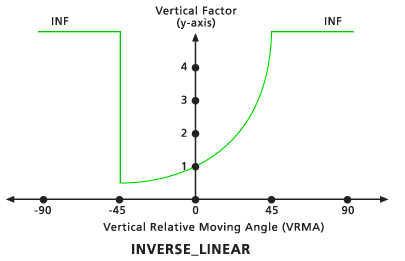
Invers Linear
Die VFs werden von den invertierten Werten einer geraden Linie im VRMA-VF-Koordinatensystem bestimmt. Die Linie schneidet die Y-Achse entsprechend dem VF-Faktor am Null-Faktor-Wert. Die Neigung der Linie kann mit dem Modifizierer Neigung angegeben werden. Wenn keine Neigung identifiziert wird, beträgt der Standard -1/45 (angegeben als 0,02222). Der niedrige Standard-Schnittwinkel beträgt -45 Grad, der hohe Standard-Schnittwinkel beträgt 45 Grad.
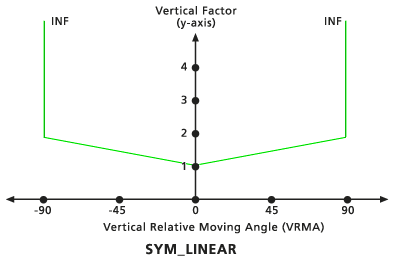
Symmetrisch Linear
Dieser vertikale Faktor besteht aus zwei linearen Funktionen relativ zu den VRMAs, die zur VF (Y)-Achse symmetrisch sind. Beide Linien schneiden die Y-Achse am für den Null-Faktor festgelegten VF-Wert. Die Neigung der Linien wird als einfache Neigung relativ zum positiven VRMA mithilfe des Neigung Vertikal-Faktor-Modifizierers definiert, der die negativen VRMAs spiegelt. Die Standard-Neigung ist 1/90 (angegeben als 0,01111). Der niedrige Standard-Schnittwinkel beträgt -90 Grad, der hohe Standard-Schnittwinkel beträgt 90 Grad.
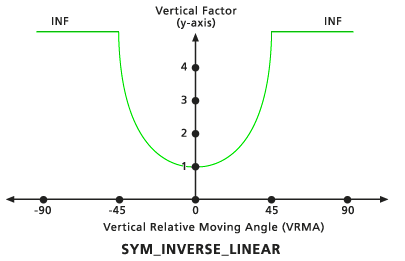
Symmetrisch Invers Linear
Dieser vertikale Faktor ist die Umkehrung des Schlüsselworts Symmetrisch Linear für den vertikalen Faktor. Er besteht aus zwei invers-linearen Funktionen relativ zu den VRMAs, die symmetrisch zur VF-(Y-)Achse sind. Beide Linien schneiden die Y-Achse am VF-Wert 1. Die Neigung der Linien wird als einfache Neigung relativ zum positiven VRMA mithilfe des Neigung Vertikal-Faktor-Modifizierers definiert, der die negativen VRMAs spiegelt. Die Standard-Neigung ist -1/45 (angegeben als 0,02222). Der niedrige Standard-Schnittwinkel beträgt –45 Grad, der hohe Standard-Schnittwinkel beträgt 45 Grad.
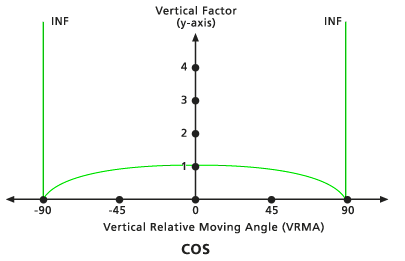
Cos
Der VF wird von der Kosinusfunktion des VRMA bestimmt. Der niedrige Standard-Schnittwinkel beträgt -90 Grad, der hohe Standard-Schnittwinkel beträgt 90 Grad. Der Standardwert für Cos-Potenz ist 1,0.
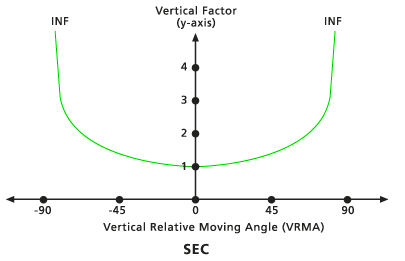
Sec
Der VF wird von der Sekantenfunktion des VRMA bestimmt. Der niedrige Standard-Schnittwinkel beträgt -90 Grad, der hohe Standard-Schnittwinkel beträgt 90 Grad. Der Standardwert für Sec-Potenz ist 1,0.
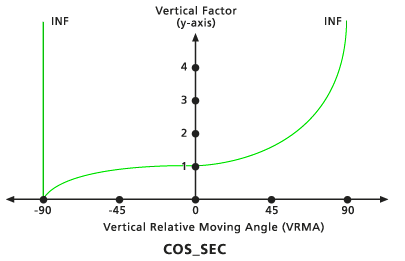
Cos - Sec
Wenn der VRMA negativ ist, wird der VF von der Kosinusfunktion des VRMA bestimmt. Wenn der VRMA positiv ist, wird der VF von der Sekantenfunktion des VRMA bestimmt. Der niedrige Standard-Schnittwinkel beträgt -90 Grad, der hohe Standard-Schnittwinkel beträgt 90 Grad. Die Standardwerte für Cos-Potenz und Sec-Potenz lauten beide 1,0.
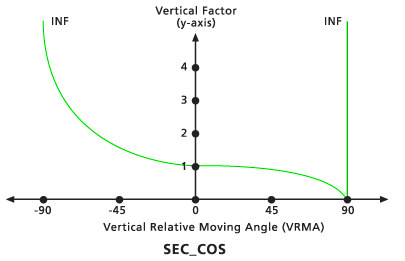
Sec - Cos
Wenn der VRMA negativ ist, wird der VF von der Sekantenfunktion des VRMA bestimmt. Wenn der VRMA positiv ist, wird der VF von der Kosinusfunktion des VRMA bestimmt. Der niedrige Standard-Schnittwinkel beträgt -90 Grad, der hohe Standard-Schnittwinkel beträgt 90 Grad. Die Standardwerte für Sec-Potenz und Cos-Potenz lauten beide 1,0.
Tabelle
Die Tabelle ist eine ASCII-Datei mit zwei Spalten in jeder Zeile.
Die erste Spalte identifiziert den VRMA in Grad und die zweite Spalte identifiziert den VF. Jede Zeile gibt einen Punkt an. Zwei aufeinander folgende Punkte erzeugen im VRMA-VF-Koordinatensystem ein Liniensegment. Die Winkel müssen in aufsteigender Reihenfolge angegeben und zwischen -90 und 90 liegen. Der VF-Faktor für einen beliebigen VRMA-Winkel unter dem ersten (niedrigsten) Eingabewert oder über dem finalen (größten) Eingabewert wird auf unendlich festgelegt. Ein unendlicher VF wird durch -1 in der ASCII-Tabelle dargestellt.
Im Folgenden sehen Sie ein Beispiel einer Vertikal-Faktor-ASCII-Tabelle. Die Einheiten der ersten Spalte sind Grad, während die Einheiten der zweiten Spalte Stunden pro Meter sind.
-90 -1
-80 -1
-70 2.099409721
-60 0.060064462
-50 0.009064613
-40 0.00263818
-30 0.001055449
-20 0.000500142
-10 0.00025934
0 0.000198541
10 0.000368021
20 0.000709735
30 0.001497754
40 0.003743755
50 0.012863298
60 0.085235529
70 2.979204206
80 -1
90 -1Modifikatoren für den vertikalen Faktor
Sie können die VRMA-Funktion mithilfe von Modifikatoren, die eine Verfeinerung der vertikalen Faktoren ermöglichen, weiter steuern. Es gibt möglicherweise einen Schwellenwertwinkel, bei dem die Kosten, sollte der VRMA ihn überschreiten, so groß sind, dass ein Bewegen verhindert wird. Dieser Schwellenwert wird als Schnittwinkel bezeichnet. Dem VF wird ein unendlicher Wert zugewiesen, wenn der VRMA diesen Wert überschreitet.
Das Diagramm für den vertikalen Faktor hat sowohl untere als auch obere Schnittwinkel, im Gegensatz zum Diagramm für den horizontalen Faktor, das nur einen einzelnen Schnittwinkel hat.
Für jede dieser Funktionen können mithilfe dieser Modifikatoren Schnittwinkel festgelegt werden. Die trigonometrischen Kurven können um eine Potenz erhöht werden, der Null-Faktor kann den Y-Achsen-Schnittwinkel für die nicht trigonometrischen Funktionen verändern, und die Neigung der Linien in den linearen Funktionen kann definiert werden.
Null-Faktor
Mit diesem Modifikator wird der vertikale Faktor festgelegt, der verwendet wird, wenn der VRMA 0 ist. Dieser Faktor positioniert den Y-Schnittpunkt der angegebenen Funktion.
Tiefer Schnittwinkel
Dieser Modifikator ist der VRMA-Grad, der den niedrigeren Schwellenwert definiert, unter dem (kleiner als) die VFs auf unendlich festgelegt werden, unabhängig von den angegebenen Schlüsselwörtern für den vertikalen Faktor.
Hoher Schnittwinkel
Dieser Modifikator ist der VRMA-Grad, der den oberen Schwellenwert definiert, über den hinaus (größer als) die VFs auf unendlich festgelegt werden, unabhängig von den angegebenen Schlüsselwörtern für den vertikalen Faktor.
Neigung
Dieser Modifikator identifiziert die Neigung der geraden Linien im VRMA-VF-Koordinatensystem für die Schlüsselwörter Linear, Invers Linear, Symmetrisch Linear und Symmetrisch Invers Linear. Neigung wird als Anstieg im Verlauf der Länge (eine 30-Grad-Neigung ist z. B. 1/30, die als 0,03333 angegeben wird) angegeben. Ein Beispiel für eine lineare Funktion mit einer Neigung von 1/90 finden Sie im Linear-VRMA-Diagramm.
Potenz
Dieser Modifikator ist die Potenz, um die die Werte angehoben werden.
Cos-Potenz
Der Modifikator ist die Potenz, um die die nicht negativen Werte der Sec-Cos-VRMA-Funktion und die negativen Werte der Cos-Sec-VRMA-Funktion angehoben werden. Der VF-Wert wird folgendermaßen bestimmt:
VF = cos(VRMA)powerSec-Potenz
Der Modifikator ist die Potenz, um die die nicht negativen Werte der Cos-Sec-VRMA-Funktion und die negativen Werte der Sec-Cos-VRMA-Funktion angehoben werden. Der VF-Wert wird folgendermaßen bestimmt:
VF = sec(VRMA)powerTabellenname
Dieser Modifikator identifiziert den Namen der ASCII-Datei, die mit dem Schlüsselwort Tabelle für den vertikalen Faktor verwendet werden soll.
Referenzen
Tobler, Waldo (1993) Three Presentations on Geographical Analysis and Modeling: Non-Isotropic Geographic Modeling; Speculations on the Geometry of Geography; and Global Spatial Analysis (93-1) Abgerufen unter https://escholarship.org/uc/item/05r820mz