Nach dem Berechnen der angepassten geradlinigen Entfernung können Sie mit dem horizontalen Faktor die Geschwindigkeit steuern, mit der die Entfernung zurückgelegt wird. Sie können die Geschwindigkeit auch mit der Kostenoberfläche, den Merkmalen des sich bewegenden Objekts und dem vertikalen Faktor steuern.
Der horizontale Faktor ist der erforderliche Aufwand zum Überwinden eines Einflusses bzw. die dadurch gewonnene Unterstützung beim Bewegen durch eine Landschaft. Ein Beispiel für einen horizontalen Einfluss ist der Wind, wenn die Bewegung über Land erfolgt, und beim Fortbewegen über ein Gewässer sind es Strömungen. Der horizontale Faktor kann beeinflussen, wie die Entfernung zurückgelegt wird. Ein Radfahrer muss bei Gegenwind mehr Kraft aufwenden, oder er legt Entfernungen mit einer langsameren Geschwindigkeit zurück. Fahrradfahren mit Rückenwind erfordert weniger Anstrengung, und Seitenwinde liegen dazwischen. Wenn die Entfernung für diesen Einfluss geändert wird, kann die Geschwindigkeit erfasst werden, mit der die Route zurückgelegt wird.

Wenn der Wind den Radfahrer in einem 45-Grad-Winkelversatz von hinten trifft, nutzt der Wind dem Radfahrer, aber weniger als ein Wind, der direkt von hinten bläst (0-Grad-Versatz).
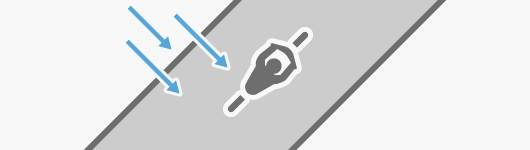
Der horizontale Faktor ist ein verstärkender Modifikator bei Entfernungsberechnungen.
Die Richtung des horizontalen Einflusses für jede Zelle wird im Horizontal-Raster ermittelt. Der horizontale Faktor hängt von der Richtung der Route ab. Mit dem Parameter Reiserichtung der Quelleneigenschaften können Sie definieren, ob die Route zur Quelle oder von ihr weg verläuft. Das Bewegen zu oder das Entfernen von einer Quelle ändert die Richtung, aus der die Route in eine Zelle führt. Die Route trifft dann in einem anderen Winkel auf den horizontalen Einfluss. Dadurch ändert sich der Multiplikator für den horizontalen Faktor. Weitere Informationen zur Interaktion von Reiserichtung und horizontalem Faktor und den Einfluss auf die Kostenentfernung finden Sie unter Einbinden von Wind in die Analyse im Thema zu Quelleneigenschaften.
Verwendungsbeispiele für den horizontalen Faktor
Der horizontale Faktor kann beispielsweise in den folgenden Szenarien verwendet werden:
- Bestimmen Sie die Route für ein Schiff, indem Sie den Einfluss Meeresströmungen berücksichtigen, die die zu verwendende Route ändern können. Dabei wird eine konstante Strömungsgeschwindigkeit im Untersuchungsgebiet vorausgesetzt.
- Ermitteln Sie den Unterschied bei der Flugzeit eines Flugzeugs, das von New York City nach Los Angeles und von Los Angeles nach New York City fliegt. Das Fliegen von Osten nach Westen dauert länger, da Gegenwind herrscht, und beim Fliegen von Westen nach Osten nicht. Dabei wird eine konstante Windgeschwindigkeit vorausgesetzt.
- Schlagen Sie einen Wanderweg vor, der sich möglichst eng an Konturlinien orientiert. Gebiete mit steilen Neigungen werden als Barrieren behandelt oder als Eingabe im Kosten-Reibungs-Raster verwendet, um die Baukosten für Strecken zu erhöhen, an denen der Weg Konturlinien folgt, aber gefährlich steile Neigungen kreuzt.
- Erstellen Sie in einem Gebiet eine abfallende Abwasserleitung, wobei die Leitung der steilsten Neigungsrichtung folgt.
Einbinden des horizontalen Faktors
Die Entfernungsanalyse kann konzeptionell in die folgenden verwandten Funktionsbereiche unterteilt werden:
- Berechnen Sie die geradlinige Entfernung, und passen Sie die Berechnungen optional mit einem Barriere- oder Oberflächen-Raster an.
- Sobald die geradlinige Entfernung berechnet wurde, kann optional die Geschwindigkeit, mit der die Entfernung zurückgelegt wird, durch eine Kostenoberfläche, Quelleneigenschaften, einen vertikalen Faktor und einen horizontalen Faktor ermittelt werden. Erstellen Sie ein Raster für die akkumulative Entfernung.
- Verbinden Sie Regionen über die resultierende akkumulative Entfernungsoberfläche mithilfe eines optimalen Netzwerks, spezifischer Pfade oder eines Korridors miteinander.
Bestimmen Sie im zweiten Funktionsbereich die Geschwindigkeit, mit der die Entfernung zurückgelegt wird, unter Berücksichtigung eines horizontalen Faktors, wie unten veranschaulicht.
Ein Boot startet in einem Jachthafen (der gelbe Punkt) und fährt zu einem zweiten Jachthafen (der orangefarbene Punkt). Die violette Linie zeigt die kürzeste gradlinige Reiseroute zwischen beiden Jachthäfen, die die Inseln umgeht.
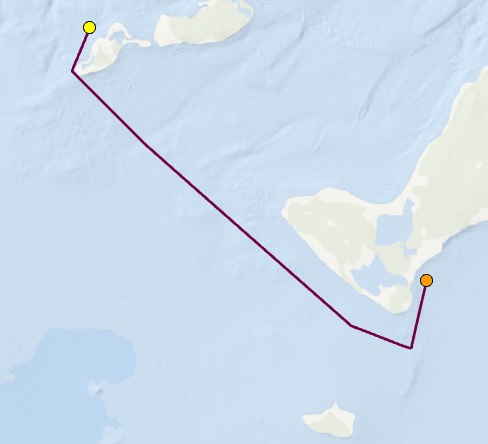
Eine Strömung verläuft jedoch von Nordwesten nach Südosten (das graue Polygon). Unter Berücksichtigung der Strömung ist die magentafarbene Linie die schnellste Route vom ersten Jachthafen (der gelbe Punkt) zum zweiten Jachthafen (der orangefarbene Punkt).
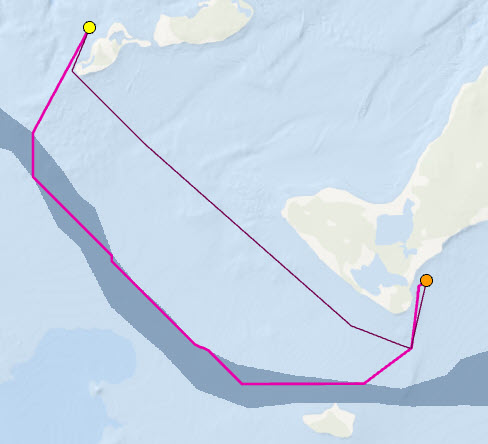
Wenn ein Horizontal-Raster eingebunden wird, ist die Reiserichtung von Bedeutung. In diesem Beispiel sind die Kosten und die Route anders, je nachdem, ob die Strecke vom ersten Jachthafen zum zweiten Jachthafen oder vom zweiten Jachthafen zurück zum ersten zurückgelegt wird.
Erstellen einer Entfernungskarte unter Verwendung eine horizontalen Faktors
Führen Sie die folgenden Schritte aus, um eine Entfernungskarte unter Berücksichtigung eines horizontalen Faktors zu erstellen:
- Öffnen Sie das Werkzeug Entfernungsakkumulation.
- Geben Sie im Parameter Eingabe-Raster oder Feature-Quellen-Daten eine Quelle an.
- Geben Sie einen Namen für das Ausgabe-Entfernungs-Raster an.
- Erweitern Sie die Kategorie Kosten im Verhältnis zur horizontalen Bewegung.
- Geben Sie ein Raster für den horizontaler Faktor für den Parameter Eingabe-Horizontal-Raster an.
Dieses Raster bestimmt die Richtung des horizontalen Einflusses für jede Zelle.
- Geben Sie den Wert für Horizontaler Faktor an.
Dieser Parameter identifiziert den Multiplikator, der angewendet wird, um zu erfassen, wie der horizontale Faktor das Zurücklegen der Entfernung beeinflusst.
- Klicken Sie auf Ausführen.
Der horizontale Faktor beeinflusst die Geschwindigkeit, mit der die Entfernung zurückgelegt wird.
Um die Geschwindigkeit zu ändern, mit der die Entfernung zurückgelegt wird, und um den Einfluss des horizontalen Faktors zu berücksichtigen, führt das Werkzeug intern zwei Aktionen aus:
- Über das Raster für den horizontalen Faktor berechnen, wie der horizontale Faktor beim Bewegen von einer Zelle in die nächste berücksichtigt wird. Dies wird als horizontaler relativer Bewegungswinkel (HRMA) bezeichnet.
- Identifizieren, wie der HRMA die Geschwindigkeit ändert, mit der die Entfernung zurückgelegt wird
Berechnen des HRMA
Um den gesamten HF für die Bewegung zwischen Zellen zu berechnen, muss der HF der Verarbeitungszelle (Ausgangszelle) bis zur Kante der Zelle, für die Sie die Entfernung berechnen (Zielzelle), sowie der HF von der Kante der Zielzelle zum Mittelpunkt bestimmt werden.
Zuerst muss die horizontale Richtung festgelegt werden. Die horizontale Richtung wird in Grad von 0 bis 360 gemessen. Der Startpunkt ist in Richtung Norden der Verarbeitungszeile, und die Zunahme erfolgt im Uhrzeigersinn.
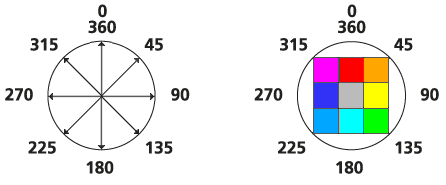
Die horizontale Richtung wird durch den Wert, der jeder Zellenposition auf dem Eingabe-Raster für den horizontalen Faktor zugewiesen wurde, definiert. Üblicherweise wird die Richtung mit den niedrigsten horizontalen Kosten für die Bewegung im Hinblick auf die Verarbeitungszelle identifiziert.
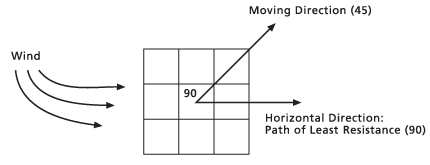
Nachdem die horizontale Richtung definiert wurde, muss relativ zu horizontalen Richtung die Position der Zelle bestimmt werden, in die die Bewegung erfolgt (Zielzelle). Die Richtung der Zielzelle relativ zur vorherrschenden horizontalen Richtung in der Verarbeitungszelle ist die horizontale Bewegungsrichtung. Der Winkel der Zielzelle von der horizontalen Richtung, wie vom Raster für den horizontalen Faktor definiert, ist der HRMA.
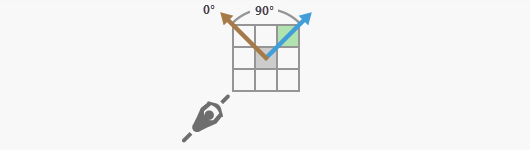
Die Gradanzahl von der festgelegten horizontalen Richtung ist relevant, nicht die Seite der festgelegten Richtung.
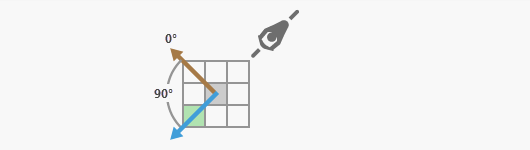
Identifizieren des HF-Multiplikators
Sobald der HRMA bestimmt wurde, wird ein Diagramm verwendet, um den Multiplikator für den horizontalen Faktor zu bestimmen. Der HF ist auf der Y-Achse und der HRMA ist auf der X-Achse.
Im oben stehenden Beispiel hat die Zelle, deren horizontalen Faktor Sie berechnen, von der horizontalen Richtung einen HRMA von 90 Grad, wie von der Verarbeitungszelle auf dem Eingabe-Raster für den horizontalen Faktor definiert. Wenn das Diagramm Linear für den horizontalen Faktor verwendet wird, betragen die Kosten für den horizontalen Faktor 1,61. Gehen Sie im folgenden Diagramm bei 90 auf der X-Achse nach oben zur grünen Funktionslinie, und folgen Sie der Funktionslinie zum Multiplikator für den horizontalen Faktor auf der Y-Achse.
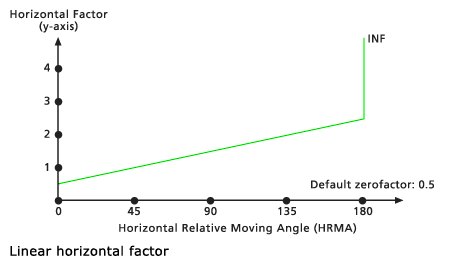
Die HRMA-Werte können zwischen -180 und 180 Grad liegen. Im Diagramm für den horizontalen Faktor sind jedoch nur Werte von 0 bis 180 auf der X-Achse vorhanden, da angenommen wird, dass das Diagramm um die Achse für den horizontalen Faktor symmetrisch (gespiegelt) ist. Dies bedeutet, dass der HRMA 90 den gleichen horizontalen Faktor hat wie der HRMA -90. INF bedeutet, dass die Linien ins Unendliche gehen.
Dieser gleiche Prozess wird für das Segment von der Kante der Zielzelle zum Zentrum ausgeführt. Die Bewegungsrichtung bleibt gleich, doch die für die Berechnung verwendete horizontale Richtung ist die vorherrschende horizontale Richtung an der Zielzelle. Das Teilen des Reise-Links zwischen zwei Zellen in zwei Segmente (eine Hälfte des Segments liegt in der Verarbeitungszelle und die andere Hälfte in der Zielzelle) führt zu einem genaueren horizontalen Faktor. Beim Verlassen der Verarbeitungszelle trifft die Route auf den horizontalen Faktor, der mit der Verarbeitungszelle verknüpft ist. Beim Eintritt in die Zielzelle gilt der mit der Zielzelle verknüpfte horizontale Faktor. In der Entfernungsformel wird der horizontale Faktor jedes Segments mit seinen jeweiligen Kostenfaktoren multipliziert, die über das Kosten-Raster bestimmt wurden, sofern eines eingegeben wurde.
Die Funktionen für den horizontalen Faktor, mit denen Sie die Wechselwirkungen der Route mit den Einflüssen des horizontalen Faktors, auf die sie trifft, erfassen können, sind Binär, Vorwärts, Linear, Invers Linear und Tabelle.
Hinweis:
Der horizontale Faktor ist ein Multiplikator. Beim Angeben der Einheiten ist Vorsicht geboten, wenn der horizontale Faktor mit einer Kostenoberfläche, mit Quelleneigenschaften oder mit einem vertikalen Faktor kombiniert wird. Wenn eine Kostenoberfläche eingegeben wird, sollte der horizontale Faktor im Allgemeinen eine Multiplikatoranpassung der Rate der Einheiten für die Kostenoberfläche sein. Wenn Zeit die Einheit für die Rate der Kostenoberfläche ist, sollte der horizontale Faktor ein Modifikator von Zeit sein. Die Einheiten für die Rate können nur durch einen dieser Faktoren definiert werden. Die anderen Faktoren haben keine Einheiten, und ihre Werte sind verstärkende Modifikatoren der angegebenen Einheiten.
Beispielanwendung, die einen horizontalen Faktor verwendet
Im Folgenden wird eine Beispielanwendung beschrieben, die einen horizontalen Faktor verwendet.
Verwenden eines horizontalen Faktors für den Bau eines Weges
Sie möchten einen Weg zwischen zwei vorhandenen Routenanfängen bauen. Der Weg soll so eng wie möglich Konturlinien folgen, damit Wanderer nicht unnötig bergauf oder bergab gehen müssen. In der Abbildung unten wird der erste Versuch mit der roten Route dargestellt. Diese Route hat einige Schwächen. Sie überquert offene Felswände, wo Bau und Instandhaltung teuer werden. Der Weg könnte dann deutlich sichtbar sein, und der Bau führt zu großen Umwelteinflüssen. Der zweite Versuch wird von der gelben Route dargestellt und erscheint geeigneter. Als Eingabe für die Analyse wurde eine Kostenoberfläche verwendet, die die Kosten des Wegebaus in Gebieten mit starker Neigung erhöht.

Das Raster für den horizontalen Faktor für beide Routen wird mit dem Werkzeug Oberflächenparameter aus einer Höhenoberfläche mit einer Auflösung von 1 Meter erstellt. Ein temporäres Ausrichtungs-Raster wurde erstellt, das die Richtung der maximalen Neigung zeigt, die Menschen bewältigen können (etwa 5 Meter). Dann wurde Map Algebra angewendet, um die Ausrichtungs-Azimuts um 90 Grad zu drehen. Das Ergebnis ist ein Raster für den horizontalen Faktor, das die Richtung der Konturlinien in jeder Zelle identifiziert. Schließlich wurde eine symmetrische Funktion für den horizontalen Faktor verwendet, um die Bewegung zu beschränken, die nicht die Richtung der Konturlinien hat.
Für die gelbe Route wurde eine Kostenoberfläche eingegeben, die den Wegebau in Gebieten mit starker Neigung verhindert.
Weitere Informationen
Die folgenden Abschnitte enthalten weitere Informationen zu horizontalen Faktoren.
Horizontale Faktoren
Um die Funktion für den horizontalen Faktor zu definieren, die zur Bestimmung des Multiplikators für den horizontalen Faktors verwendet wird, können Sie eine vorhandene Funktion aus den Diagrammen der Software auswählen oder eine benutzerdefinierte Funktion aus einer ASCII-Datei erstellen. Die folgenden Funktionen für den horizontalen Faktor sind in den Werkzeugen Entfernungsakkumulation und Entfernungsallokation verfügbar:
Optionen, Modifikatoren und Standardwerte für den horizontalen Faktor
| Funktion | Null-Faktor | Schnittwinkel | Neigung | Seitenfaktor |
|---|---|---|---|---|
Binär | 1 | 45 | N.z. | N.z. |
Vorwärts | 0,5 |
N.z. | N.z. | 1 |
Linear | 0,5 | 181 | 1.111E-02 | N.z. |
Invers Linear | 2 | 180 | -1.111E-02 | N.z. |
Im Folgenden werden die einzelnen Funktionen für den horizontalen Faktor beschrieben. Jede Funktion kann durch eine Reihe von Modifikatoren weiter optimiert werden. Die Modifikatoren sind im folgenden Abschnitt beschrieben.
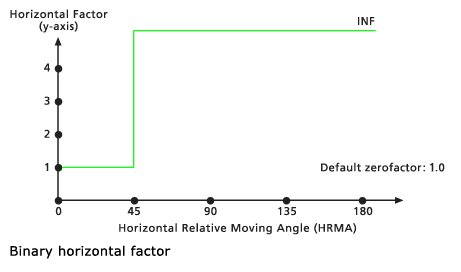
Binär
Wenn der HRMA geringer als der Ausschnittwinkel ist, wird der HF zum Navigieren im Abschnitt der Zelle auf den Wert für den Null-Faktor festgelegt. Wenn der HRMA größer als der Schnittwinkel ist, wird der HF für den Abschnitt auf unendlich festgelegt. Der Standard-Schnittwinkel beträgt 45 Grad. Der Standard-Null-Faktor beträgt 1,0.
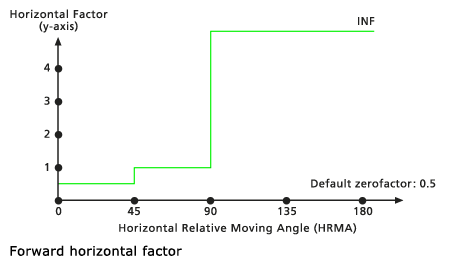
Vorwärts
Wenn der HRMA geringer als 45 Grad in einem Bewegungsabschnitt ist, wird der HF auf den Wert für den Null-Faktor festgelegt. Wenn der HRMA größer als oder gleich 45 Grad und kleiner als 90 Grad ist, wird der HF auf den Wert für den Seitenfaktor festgelegt. Ist kein Seitenfaktor festgelegt, wird der Standard-Seitenfaktor 1 verwendet. Wenn der HRMA gleich oder kleiner als 90 Grad ist, wird der HF auf unendlich festgelegt. Der Standard-Null-Faktor beträgt 0,5.
Linear
Die HFs werden von einer geraden Linie im HRMA-HF-Koordinatensystem bestimmt. Die Linie schneidet die Y-Achse entsprechend dem HF-Faktor am Wert Null-Faktor. Die Neigung der Linie kann mit dem Modifizierer Neigung angegeben werden. Wenn keine Neigung identifiziert wird, beträgt der Standard 0,5/45 oder 1/90 (angegeben als 0,01111). Der Standard-Schnittwinkel ist 181 Grad, der keinem Ausschnitt entspricht. Der Standard-Null-Faktor beträgt 0,5.

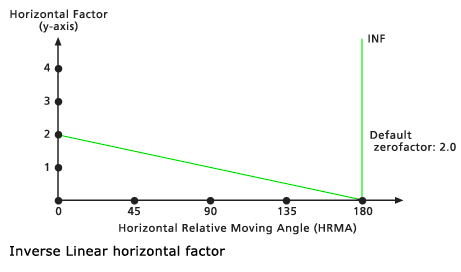
Invers Linear
Die HFs werden von den invertierten Werten einer geraden Linie im HRMA-HF-Koordinatensystem bestimmt. Die Linie schneidet die Y-Achse entsprechend dem HF-Faktor am Wert Null-Faktor. Die Neigung der Linie kann mit dem Modifizierer Neigung angegeben werden. Wenn keine Neigung identifiziert wird, beträgt der Standard -2/180 oder -1/90 (angegeben als 0,01111). Der Standard-Schnittwinkel ist 181 Grad, der keinem Ausschnitt entspricht. Der Standard-Null-Faktor beträgt 2,0.
Tabelle
Ein Diagramm kann mit einer in einem beliebigen Texteditor erstellten ASCII-Datei definiert werden. Die Datei besteht aus zwei Spalten mit Werten in jeder Zeile. Der erste Wert identifiziert den HRMA in Grad und die zweite Spalte den HF. Jede Zeile gibt einen Punkt auf dem Diagramm an. Zwei aufeinander folgende Punkte definieren im HRMA-HF-Koordinatensystem ein Liniensegment. Die HRMA-Winkel müssen in aufsteigender Reihenfolge eingegeben werden. Der HF-Faktor für einen beliebigen HRMA-Winkel unter dem ersten (niedrigsten) Eingabewert oder über dem letzten (größten) Eingabewert wird auf unendlich festgelegt. Ein unendlicher HF wird durch -1 in der ASCII-Datei dargestellt.
Im Folgenden ist ein Beispiel für eine ASCII-Tabelle für den horizontalen Faktor dargestellt:
0 1.40
10 2.43
20 2.30
30 3.44
40 1.25
50 1.02
60 0.90
70 0.86
80 0.25
90 0.78
100 1.49
110 2.35
120 3.32
130 2.39
140 3.18
150 2.13
160 1.89
170 1.20
180 2.034Horizontale Faktormodifikatoren
Mehrere der HRMA-Schlüsselparameter verfügen über Modifikatoren, die angegeben werden können, um verschiedene Ergebnisse zu erreichen. Die Neigung der Linie in den Funktionen Linear und Invers linear, die Seitenwerte für die Funktion Vorwärts und der Nullfaktor können den Schnittpunkt an der Y-Achse für die Eingabefunktionen verändern, und der Schnittwinkel für beliebige HRMA-Funktionen kann gesteuert werden.
Null-Faktor
Dieser Modifikator positioniert den Y-Schnittpunkt der angegebenen Funktion. Er kann in Verbindung mit allen Funktionen für den horizontalen Faktor verwendet werden.
Schnittwinkel
Dieser Modifikator legt den HRMA-Grad-Schwellenwert fest, jenseits dessen die HFs auf unendlich festgelegt werden. Schnittwinkel kann mit einem beliebigen der angegebenen Schlüsselwörter für den horizontalen Faktor außer Vorwärts verwendet werden. Diese Funktion legt definitionsgemäß eigene Schnittwinkel fest.
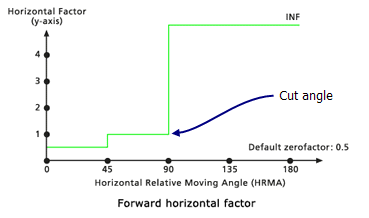
Neigung
Dieser Modifikator identifiziert die Neigung der geraden Linien im HRMA-HF-Koordinatensystem für die Schlüsselwörter Linear und Invers Linear. Neigung wird als Anstieg im Verlauf der Länge (eine 30-Grad-Neigung ist z. B. 1/30, die als 0,03333 angegeben wurden) angegeben. Ein Beispiel für eine Zeile mit einer Neigung von 1/90 finden Sie im Linear-HRMA-Diagramm.
Seitenfaktor
Dieser Modifikator identifiziert den HF-Wert, der für HRMAs zugewiesen wird, die gleich oder kleiner als 45 Grad und kleiner als 90 Grad sind, wenn das Schlüsselwort Vorwärts für den horizontalen Faktor verwendet wird. Überprüfen Sie im Forward-HRMA-Diagramm, welcher Wert über den Seitenwert 1 verfügt.
Tabellenname
Dieser Modifikator identifiziert den Namen der ASCII-Datei, die für die Option Tabelle verwendet wird.