空间数据通常具有空间自相关性,即地理位置相近的观测值往往具有相似的取值。 如果在回归模型中忽略这种空间自相关性,可能会导致有偏的参数估计和不准确的推论。
空间自回归工具旨在解决这些问题,它通过拟合空间回归模型,明确地考虑了空间依赖性。 该工具既可以执行传统的普通最小二乘回归,也可以选择以下几种全局空间回归模型:空间滞后模型、空间误差模型或空间自回归组合模型。 您可以手动指定工具使用的模型,或者让工具通过对因变量和自变量进行一系列诊断测试,自动确定最适合的模型。
这些回归模型的目标是,在存在空间依赖性的情况下,也能对回归模型进行可靠的推断。 通过使用空间回归模型,您可以对模型估计的结果更有信心,并且能够评估空间因素在模型中的影响。
可能的应用
空间自回归工具主要通过以下两种方式来处理模型中的空间依赖性:
首先,空间滞后模型适用于分析空间溢出效应,例如:
- 公共卫生和流行病学 - 在评估疾病或病毒的传播时,考虑到空间依赖性。
- 犯罪学 - 理解犯罪行为如何在地理上聚集和扩散,并考虑邻域效应。
其次,空间误差模型可以通过考虑解释变量中存在的空间依赖性,来提供无偏的模型参数估计,例如:
- 社会经济分析 - 在评估教育程度时,控制自变量中空间相关的因素。
- 房价 - 控制未观测到的、影响房产价值的空间因素,从而更清晰地分析模型中的关键变量。
模型类型
空间自回归工具可以估计三种全局空间回归模型,每种模型都以不同的方式来处理空间依赖性。 当诊断结果表明这三种空间回归模型均不适用时,则会执行普通最小二乘回归。
空间误差模型
空间误差模型 (SEM) 用于解决回归模型的残差项中存在空间自相关性的问题。 在 SEM 中,空间依赖性被视为一种干扰因素。 这种干扰因素必须被处理,才能确保推论的准确性。 SEM 模型的公式如下:
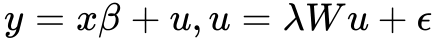
与普通最小二乘回归公式类似,因变量 (y) 由一组解释变量 (x) 和系数 (β) 预测。 不同之处在于,残差项 (u) 本身也通过一个回归方程建模。 在第二个回归方程中,残差项由空间自回归参数 λ (lambda)、空间权重矩阵 (W) 以及新的残差项 (ε) 预测。 lambda 参数量化了误差项中空间依赖性的强度,衡量了一个位置的误差项对相邻要素的误差项的影响程度。
SEM 的原理是从模型中的每个变量中消除空间自相关性,然后对经过空间过滤后的变量进行回归。 因此,系数估计值不会受到各变量中空间自相关性的显著影响。
空间滞后模型
与将空间依赖性视为干扰因素的 SEM 不同,空间滞后模型 (SLM) 将空间依赖性作为一个自变量纳入模型。 空间滞后模型适用于因变量具有较强的空间自相关性,并且存在空间溢出效应(即一个区域的变化会影响其相邻区域)的情况。 SLM 模型的公式如下:
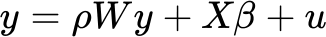
因变量由解释变量以及其自身的空间滞后项 (Wy) 预测。 空间自回归参数 ρ (rho) 衡量了一个位置的相邻要素对该位置因变量 (y) 的影响强度。 ρ 参数的较大估计值表明存在一种扩散过程,即一个位置的值会影响其相邻位置的值。 反过来,相邻要素也会对原始位置产生影响,从而形成反馈回路。
空间自回归组合模型
空间自回归组合模型 (SAC) 融合了空间误差模型和空间滞后模型中的空间自回归参数 λ 和 ρ。
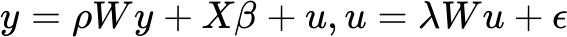
在这种模型中,我们既考虑了误差项的空间依赖性,又考虑了因变量的空间滞后效应。 SAC 模型能够用于识别因变量中的空间溢出效应,同时解决误差项中存在的空间依赖性。
选择合适的模型
默认情况下,该工具会根据一系列统计检验(称为拉格兰奇乘数 (LM) 检验,也称为 Rao 得分)自动选择最合适的模型。 模型选择过程主要遵循 Anselin 和 Rey (2014) 提出的工作流。
模型选择的决策标准如下图所示:
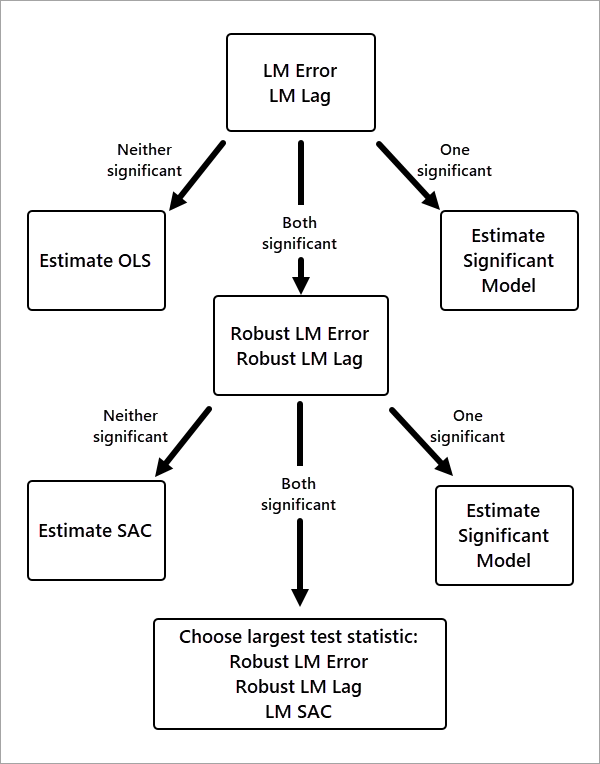
首先,进行空间滞后(LM 滞后)模型和空间误差(LM 误差)模型的 LM 检验。 如果两个检验均不显著(p 值大于 0.05),则无需使用空间模型,而是选择 OLS 模型。 如果只有一个检验显著,则选择相应的模型。
如果 LM 滞后和 LM 误差检验均显著,则进一步进行其稳健性检验。 稳健性检验包括稳健 LM 滞后检验和稳健 LM 误差检验,这些检验的要求更为严格。 如果只有一个检验显著,则选择相应的模型。
如果两个稳健性检验均显著,则进行 SAC 模型的 LM 检验。 如果三个检验均显著,则选择检验统计量最大的模型。
在极少数情况下,如果 LM 滞后和 LM 误差检验均显著,但稳健性检验均不显著,则选择 SAC 模型。
重要提示:LM 检验是一种数据驱动的模型选择方法。 它无法保证得到一个理想的模型或完美的拟合结果。 因此,请仔细检查诊断结果,并充分考虑模型的理论假设。
工具输出
该工具的主要输出包括地理处理消息中的多个表格、输出要素类,以及用于可视化模型残差的图表。
输出要素
工具的输出要素类包含以下字段:因变量、解释变量、因变量的预测值、残差、标准化残差、残差的空间滞后,以及每个要素的相邻要素数量。
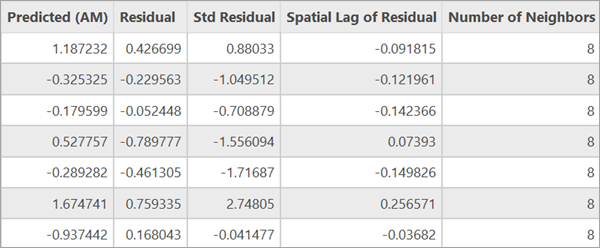
将该图层添加到地图后,要素会根据其标准化残差进行着色。 可视化标准化残差有助于识别误差项中的任何聚类模式。
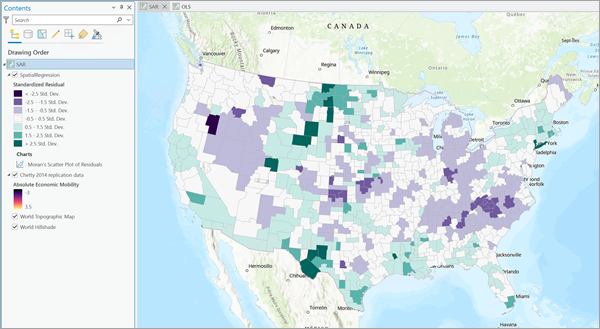
残差的颜色从深紫色渐变到深绿色。 绿色表示的区域具有正残差,说明模型高估了实际值。 紫色表示的区域具有负标准化残差。 负残差表示模型低估了实际值。
残差的莫兰散点图
输出图层包含一个散点图,以图形方式展示了残差与其空间滞后的关系。 该图 x 轴为标准化残差,y 轴为标准化残差的空间滞后。 这种图表被称为莫兰散点图。
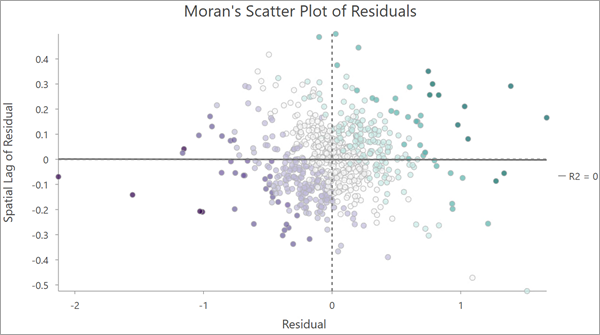
可以将该图表以 x 和 y 轴 0 点为中心划分为四个象限。 位于右上象限和左下象限的值显示出正空间自相关性。 这些位置的值与其相邻要素的值相似:分别为正值和负值。 位于左上象限和右下象限的位置显示出负空间自相关性。 这些位置的值与其相邻要素的值相反:高值被低值包围(反之亦然)。
如果残差均匀分布在四个象限中,则表明不存在明显的空间自相关性。 当回归模型表现良好且已充分考虑了空间自相关性时,通常会出现这种模式。
地理处理消息
该工具还在地理处理消息中提供多个表格,可帮助您了解每个模型的估计过程:
- 邻域和空间权重汇总
- LM 检验结果
- 模型结果汇总
- 模型诊断
在某些情况下,还会显示以下消息表格:
- 系数效应汇总
- 重合点报表
以下章节将详细描述每个表格的内容。
邻域和空间权重汇总
SEM、SLM 和 SAC 模型都需要使用空间权重矩阵,该矩阵对模型结果有显著影响。 “邻域和空间权重汇总”表格提供了关于用于拟合模型的空间权重矩阵的详细信息。 此表列出了邻域类型、权重方案、空间连通性、平均邻域大小、最小邻域大小和最大邻域大小等信息。
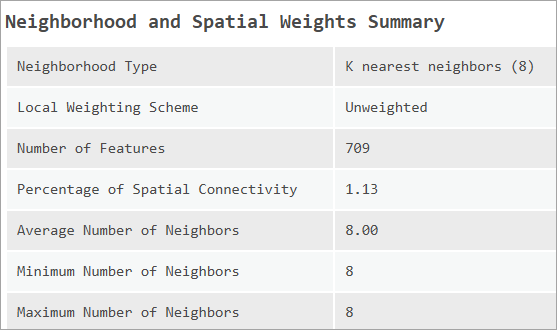
请务必注意,如果空间权重矩阵的连通性过高,工具将无法估计模型。 空间连通性百分比约为每个要素的平均相邻要素数占要素总数的百分比。 例如,对于包含 500 个要素的数据集,如果空间连通性为 0.1,则每个要素平均大约有 50 个相邻要素。 如果空间权重矩阵的连通性达到或超过 30%,则模型结果会产生偏差 (Smith, 2009)。 在这种情况下,工具将返回错误消息。
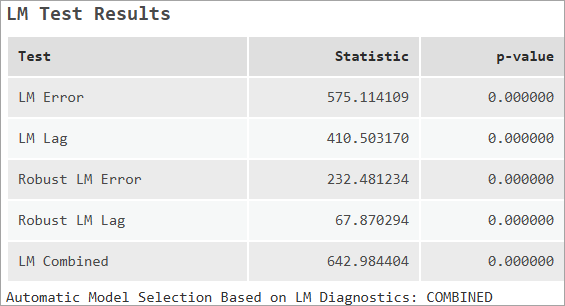
LM 检验结果
“LM 检验结果”表提供了各种检验的拉格兰奇乘数诊断信息。 该表还显示了基于选择合适的模型部分中的流程图所选择的模型类型。
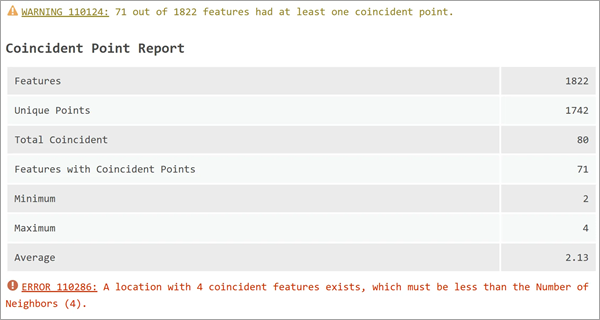
重合点报表
重合点(坐标相同的点)可能会导致空间回归中出现各种问题,例如为所有相邻要素创建权重为零的情况。 如果输入要素中存在重合点,将显示“重合点报表”,其中包含要素总数、唯一位置数量,以及所有要素的最小、最大和平均重合点数量。 此外,还可能会显示由重合点引起的警告和错误。
模型诊断
“模型诊断”表显示了重要的诊断信息,如因变量、要素数量、自由度以及所使用的模型。
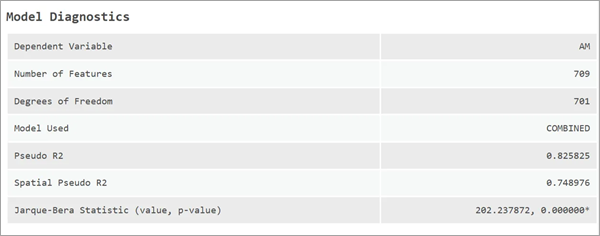
如果选择了 OLS 模型,则该表中会显示调整后的 R 平方值。 但是,对于所有空间模型,则显示伪 R 平方值。 对于 SLM 和 SAC 模型,还将显示空间伪 R 平方值。 这些将在后续内容中进行详细讨论。
此外,还会报告 Jarque-Bera 统计量。 如果该统计量结果显著,则表明模型的残差不服从正态分布。 虽然这些模型是使用对非正态性具有鲁棒性的方法进行估计的,但该检验结果可能表明模型存在设定误差或数据中存在异常值。
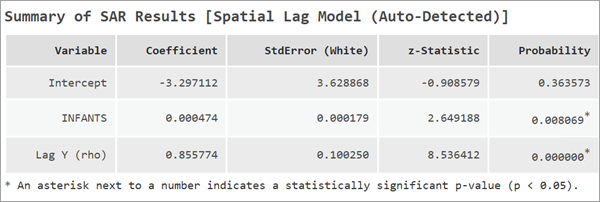
解读空间滞后模型的结果
空间滞后模型会报告一个额外的系数,称为滞后 Y (rho)。 这表示因变量的空间滞后项。 该变量的系数衡量了因变量的空间依赖性的强度和方向。 rho 值必须介于 -1 和 1 之间。 较大的滞后 Y 值表明存在较强的空间反馈效应。
请注意,一个位置的解释变量发生变化可能会影响另一位置的因变量值,这种现象被称为空间溢出。 在存在空间溢出的情况下,在解读回归系数时,必须同时考虑空间溢出效应。
影响和系数效应
除了回归系数外,还会报告一种称为“影响”的度量指标。 “影响”指标有助于评估每个解释变量的空间溢出效应。 它们分为直接影响、间接影响和总影响。 计算“影响”指标有多种方法,此工具报告的是简单影响。 “系数效应汇总”消息表展示了直接效应、间接效应和总效应的计算结果。
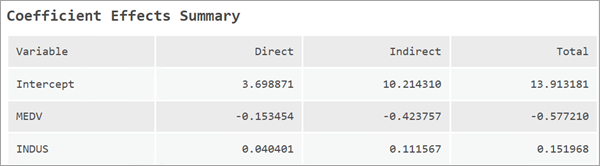
直接效应用于衡量解释变量自身发生单位变化时,对因变量在该位置产生的影响大小。 在简单影响的情况下,直接效应的值与 Beta 系数相同。
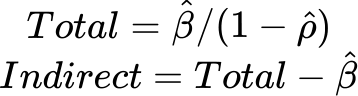
间接效应衡量的是某个解释变量发生单位变化时,对相邻位置因变量产生的影响大小。 需要注意的是,效应值的大小很大程度上取决于空间权重矩阵的构建方式。
标准误差
空间滞后模型默认会报告稳健标准误差。 然而,在拟合空间滞后模型后,残差中可能仍然存在显著的空间自相关性。 Anselin-Kelejian (AK) 检验是一种诊断性测试,用于判断模型残差中是否还存在明显的空间依赖性。
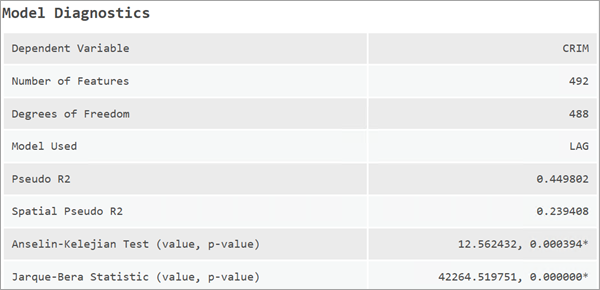
如果 AK 检验结果显著(p 值小于 0.05),则会使用另一种标准误差的计算方法,即异方差和自相关稳健 (HAC) 标准误差。 HAC 标准误差是一种非参数的标准误差计算方法,适用于处理空间自相关的情况。
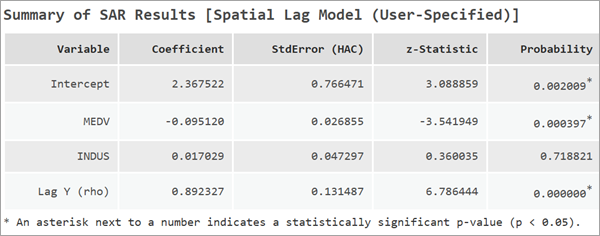
HAC 标准误差会考虑数据的空间分布,它使用一个单独的空间权重矩阵来实现这一点。 这个空间权重矩阵通过 k 近邻算法来确定每个要素的邻域,并将目标要素纳入其自身邻域中。 每个邻域的权重则通过三角核函数进行建模。
伪 R 平方和空间伪 R 平方
由于空间滞后模型将因变量的空间滞后项作为解释变量,因此无法直接使用传统的线性回归预测方法进行预测。 如果使用因变量的空间滞后项来预测因变量,会导致预测结果过于自信(即过高估计)。 为了解决这个问题,引入了空间伪 R 平方作为替代指标。
空间伪 R 平方的计算不直接使用因变量的空间滞后项。 相反,它利用空间权重矩阵以及 λ 的估计值来生成 Wy-hat 的预测值,并用该预测值代替 Wy 进行计算。
最终,利用这些预测值计算出一个传统的伪 R 平方值。 因此,建议报告空间伪 R 平方,而不是直接报告伪 R 平方。
需要强调的是,空间伪 R 平方与普通最小二乘法 (OLS) 结果中报告的调整后 R 平方是不同的指标。 因此,将两者进行比较是不恰当的。
解读空间误差模型的结果
在空间误差模型中,回归系数的解释方式与标准线性回归模型类似。 每个系数表示自变量变化一个单位时,因变量的变化量。 但是,SEM 还包括一个附加组成部分,即滞后残差 (lambda),它在理解模型中的空间依赖性方面起着至关重要的作用。 滞后残差 (lambda) 的系数始终介于 -0.99 和 0.99 之间。
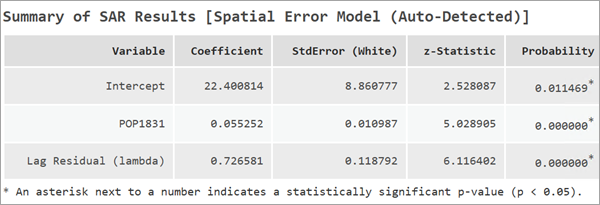
Lambda 的正值表明残差表现出空间聚类,而 lambda 的负值表明残差表现出空间离散。 lambda 的较大绝对值(正或负)也表明存在解释变量未解释的空间过程。 包括其他相关的解释变量可能会将该系数降低到更适中的水平。
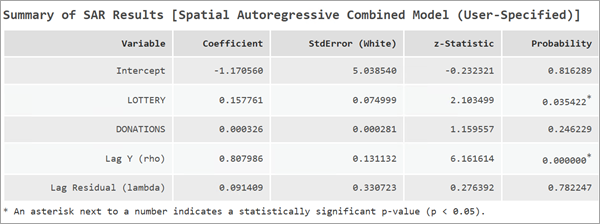
解释空间自回归组合模型结果
选择 SAC 模型时,消息中会显示适用于 SLM 和 SEM 模型的所有部分。
参考资料
使用了以下资源来实现该工具:
- Anselin, L., and Sergio J. Rey. 2014. "Modern spatial econometrics in practice: A guide to GeoDa, GeoDaSpace and PySAL." ISBN 9780986342103.
Bivand, Roger and Gianfranco Piras. 2015. "Comparing implementations of estimation methods for spatial econometrics." Journal of Statistical Software. 63: 1-36. https://doi.org/10.18637/jss.v063.i18.
Kelejian, Harry H., and Ingmar R. Prucha. 2007. "HAC estimation in a spatial framework." Journal of Econometrics. 140, no. 1: 131-154. https://doi.org/10.1016/j.jeconom.2006.09.005.
Smith, Tony E. 2009. "Estimation bias in spatial models with strongly connected weight matrices." Geographical Analysis. 41, no. 3: 307-332. https://doi.org/10.1111/j.1538-4632.2009.00758.x.