按函数重设等级工具可根据指定的变换函数重设输入栅格值的等级。 存在多种变换函数,并且每种变换函数的计算和应用各不相同。 要使用的变换函数将基于最能捕捉所研究现象的函数。 您可通过一系列输入参数进一步优化各个函数的特征。
为充分利用本部分中的信息,最好先熟悉此工具使用的基本词汇。 要了解变换函数阈值下限和阈值上限对输出值的影响,请参阅阈值下限和阈值上限对输出值的交互作用。
函数列表
下表汇总了各个函数,并提供了可转到相应函数特定讨论的链接。
适用情况:优先级随输入值增加而增加,并且优先级的增加速度因输入值增大而加快。 | |
适用情况:最高优先级围绕某个输入值,并且优先级随着输入值远离该值而降低。 | |
用于指示输入值越大优先级越高。 | |
通过线性函数重设输入值的等级。 | |
适用情况:较低输入值的优先级随着值的增加而快速增加,然后优先级的增加速度将随着输入值的进一步增加而放缓。 | |
适用情况:小输入值的优先级最高,并且 优先级随值的增加而快速降低,直到值达到较大输入值时,优先级才会逐渐停止变化。 | |
适用情况:大输入值的优先级最高,并且 优先级随值的增加而快速增加,直到值达到较大输入值时,优先级才会逐渐停止变化。 | |
在输入栅格值越大优先级越高的情况下,基于平均值和标准差重设输入数据的等级。 | |
在输入栅格值越小优先级越高的情况下,基于平均值和标准差重设输入数据的等级。 | |
适用情况:输入值非常接近中点时优先级较高。 | |
适用情况:输入值的优先级随输入值的增加而快速增加。 | |
用于指示输入栅格值越小优先级越高。 | |
适用情况:某个特定输入值的优先级最高,并且优先级随输入值远离该点而以线性方式降低。 |
函数概览与图示
将为每个函数提供一个常规概述、一个用例,以及有关特定输入参数对函数曲线的影响的详细信息。
概览
概览将介绍每个函数的基本属性和特定行为。
用例
用例将介绍一个非常适合特定函数的具体的实际示例。
参数作用
本部分将讨论形状控制参数如何影响函数。 将介绍更改参数值将如何影响曲线,并显示一个包含多个不同参数值的图表以演示影响。 还包括一个 Python 类表达式,用于演示如何构建图表中显示的变换函数。
注:
对于所显示的每个图形示例,输入都是一个值介于 0 至 500 之间的栅格。 此项特定选择不存在任何特别原因,但为使比较更为方便,所有图形均采用此项选择。 实际上,真正的输入栅格可采用任意输入值范围。
指数函数
概览
指数函数会通过应用具有指定平移和基础系数的指数函数来变换输入数据。 在适用性模型中,如果具有小输入值的位置具有最低优先级,但优先级随像元值的增大而快速升高,此时最适合使用此函数。
用例
考虑如何针对乌龟适宜性模型重设到水源距离的等级。 乌龟喜欢靠近水的位置,因为它们的活动能力有限。 随着距水体距离的扩大,距水体较远位置的优先级会迅速降低。
参数作用
输入平移
输入平移是从输入值中减去的值。 “指数”函数将应用于移位输入值以确定函数值。
基础系数
基础系数参数控制指数函数增长的急剧程度。 随着基础系数的增加,较低输入值的优先级将随着输入值的增加以较慢的速度增加,然后优先级将在较大的输入值处快速增加。 如果输入数据范围较小(例如 0 到 1)并且您想要维护最小值和最大值间的指数曲线,那么更改此参数则可能非常有用。
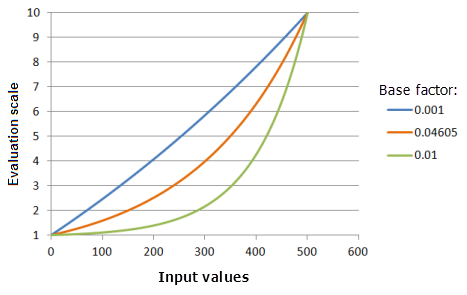
上图中使用的函数:
- TfExponential(0.002651, BaseFactor, 0, 1, 500, 10)
其中 BaseFactor 使用的值为 0.001、0.04605 和 0.01。 平移 0.002651 和基础系数 0.04605 是范围为 0 到 500 的输入数据集的默认计算参数值。
高斯函数
概览
高斯函数会通过正态分布来变换输入值。 当应用递增的评估等级时,正态分布的中点将定义优先级最高的值。 如果该中点介于阈值下限和阈值上限之间,则为至等级值分配一个等于中点的输入值。 其余输入值将从两个方向远离中点,因此它们的评估等级会降低(优先级降低),直至达到自等级值为止。 在适用性模型中,最适合使用此函数的情况是在接近已知值时优先级最高,并且优先级随输入值远离该值而降低。
用例
安装太阳能电池板时,选择正确的方向以使电池板朝向在最大限度地提高其输出方面非常重要。 对于北半球,朝南的坡向(180 度)具有最高的优先级。 并且坡向的优先级会随着朝东或朝西程度的加大而持续降低,直至在朝北时达到最低。
参数作用
中点
中点参数可定义高斯曲线的中心。 您可能希望从数据中点平移函数中点,以使较低或较高的值更加重要或者不再重要。 您希望移动中点的另一个原因是要使函数适用于数据范围外的条件值。
中点可以控制函数曲线将涵盖的输入值范围。
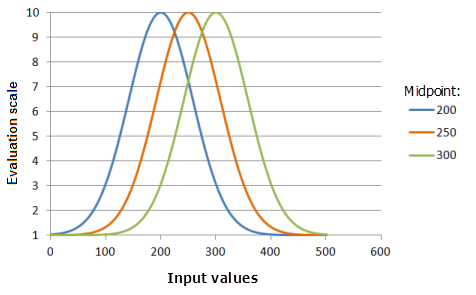
上图中使用的函数:
- TfGaussian(Midpoint, 0.000147, 0, 1, 500, 10)
其中 Midpoint) 使用的值为 200、250 和 300。 中点 250 和散度 0.0000147 是范围为 0 到 500 的输入数据集的默认计算参数值。
散度
散度参数控制自中点开始衰减的急剧程度。 此值越大,中点周围的曲线越窄(优先级下降得越快)。
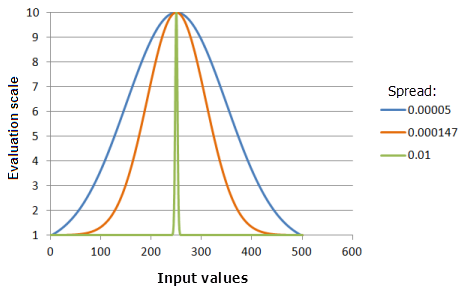
上图中使用的函数:
- TfGaussian(250, Spread, 0, 1, 500, 10)
其中 Spread 使用的值为 0.00005、0.000147 和 0.01。 中点 250 和散度 0.0000147 是范围为 0 到 500 的输入数据集的默认计算参数值。
大值 (Large) 函数
概览
大值变换函数用于输入值越大优先级越高的情况。 已定义的中点用于标识函数的过渡点。 大于中点的值具有较高的优先级,小于中点的值具有较低的优先级。 值随着远离中点而增加和减小的速度由散度形状控制参数确定。
用例
要创建商品交易适宜性模型,您可能需要重设咖啡产量条件的等级。 产量越高的位置优先级越高,优先级将以非线性方式随产量的变化而升高。
参数作用
中点
中点参数可定义此函数的过渡点。 将过渡点平移至小于输入数据中点值的位置会更改过渡点,使得中点右侧优先级较高的较大值的范围增大,优先级的提升速度也会加快。
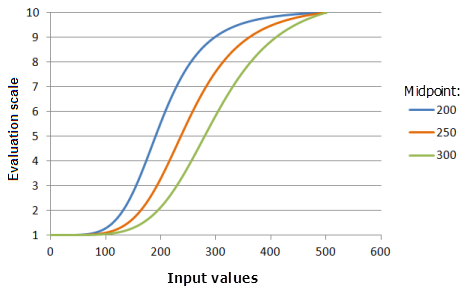
上图中使用的函数:
- TfLarge(Midpoint, 5, 0, 1, 500, 10)
其中 Midpoint 使用的值为 200、250 和 300。 中点 250 和散度 5 是范围为 0 到 500 的输入数据集的默认参数值。
散度
散度参数控制优先级升高和降低的速度。 在散度值增大时,大于中点的输入值的优先级会更快升高,直至达到阈值上限;小于中点的输入值的优先级会更快下降,直至达到阈值下限。
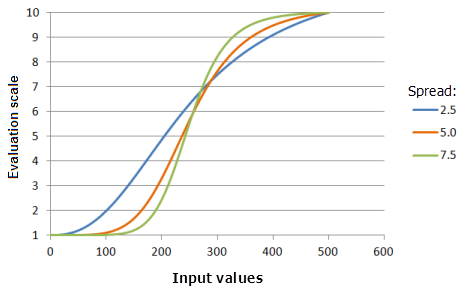
上图中使用的函数:
- TfLarge(250, Spread, 0, 1, 500, 10)
其中 Spread 使用的值为 2.5、5.0 和 7.5。 散度 5 和中点 250 是范围为 0 到 500 的输入数据集的默认参数值。
线性函数
概览
线性变换函数将在指定的最小值和最大值之间应用线性函数。 如果自等级大于至等级,则将建立负线性关系(负坡度)。
此函数最适合在值的优先级以恒定线性速度升高或降低时使用。
用例
要为野生动物栖息地创建气候变化适宜性模型,您可能需要重设野生动物高程值优先级的等级。 在研究区域内,高程值越大优先级越高。
参数作用
最小值
最小值参数可建立线性函数必须经过的第一个点。 您可能希望根据相应条件将参数值更改为输入数据最小值以外的值,使该值与现象的优先级相对应。
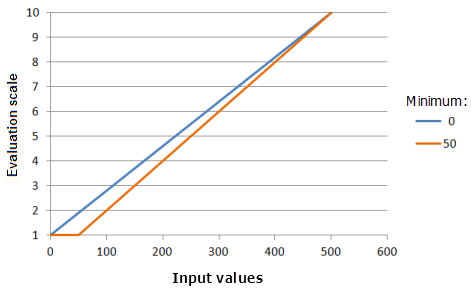
上图中使用的函数:
- TfLinear(Minimum, 500, 0, 1, 500, 10)
其中 Minimum 使用的值为 0 和 50。 最小值 0 和最大值 500 是范围为 0 到 500 的输入数据集的默认参数值。
最大值
最大值参数可建立线性函数必须经过的第二个点。 您可能希望根据相应条件将参数值更改为输入数据最大值以外的值,使该值与相关现象的优先级相对应。
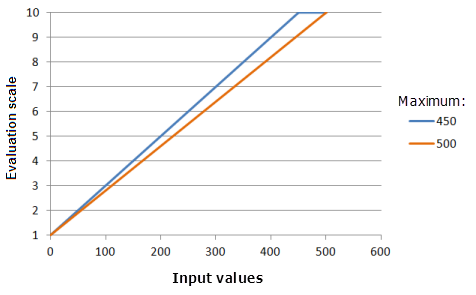
上图中使用的函数:
- TfLinear(0, Maximum, 0, 1, 500, 10)
其中 Maximum 使用的值为 450 和 500。 最小值 0 和最大值 500 是范围为 0 到 500 的输入数据集的默认参数值。
对数函数
概览
对数变换函数会通过指定的平移和系数对输入数据应用对数函数。 在适用性模型中,最适合在优先级先随输入条件值的增大而快速升高或降低然后逐渐放缓的情况下使用对数函数。
用例
要创建鸟类适宜性模型,您可能希望重设食物量条件的等级。 如果较低的食物量无法养活鸟类,则其位置将具有最低的优先级。 当食物量足够鸟类维持生存时,食物量更大的位置的优先级将快速增加,因为鸟类将更加健康。 达到特定点后,鸟类将获得充足的食物,因此食物量更大的位置虽然仍旧更加适合,但优先级的升高速度会大大降低。
参数作用
平移
平移是要从输入值中减去的值,可控制对数计算的起始输入值。 例如,在鸟类用例中,如果鸟类无法在食物少于 250 单位的位置生存,您可能希望将函数的起点平移至 250。
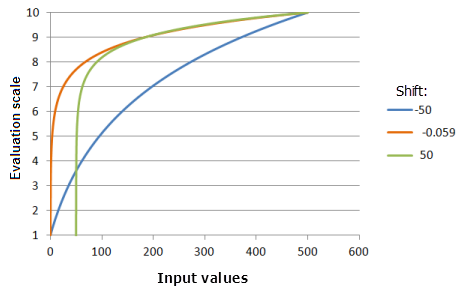
上图中使用的函数:
- TfLogarithm(Shift, 0.0046, 0, 1, 500, 10)
其中 Shift 使用的值为 -50.0、-0.059 和 50.0。 平移 -0.059 和指数 0.0046 是范围为 0 到 500 的输入数据集的默认计算参数值。
因子
系数是一个乘数,用于控制对数函数的增加速度。 如果输入值范围较小(例如 0 到 1),可更改此参数以维护最小值与最大值之间的对数曲线。
逻辑衰减函数
概览
逻辑衰减变换函数相当于在指定最小值和最大值之间采用已定义的 y 截距百分比的逻辑衰减函数。 在适宜性模型中,逻辑衰减函数最适用于较低输入值具有较高优先级的情况。 随着输入值的增加,优先级迅速下降至某一点,在该点上,优先级会因输入值达到较大值而达到最低并逐渐停止变化。
用例
要创建房屋适宜性模型,您可能需要根据电力成本条件重设到电线的距离的等级。 距离现有电线更近的位置具有较高的优先级,因为其供电成本更低。 达到相应距离后,优先级将快速降低,因为需要安装额外的变压器,从而产生附加的劳动力和设备成本。 距离最远的像元的优先级下降速度会逐渐减慢,因为这些位置的成本已经相当高,额外成本对优先级的额外影响不大。
参数作用
最小值
最小值参数控制逻辑衰减的起点。 最小值越大,优先级在此函数主要衰减部分的下降速度越快(曲线越陡)。
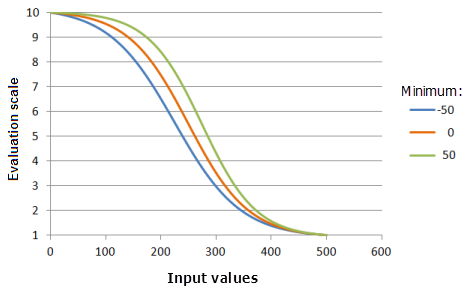
上图中使用的函数:
- TfLogisticDecay(Minimum, 500, 99, 0, 1, 500, 10)
其中 Minimum 使用的值为 -50、0 和 50。 最小值 0、最大值 500 和 y 截距百分比 99 是范围为 0 到 500 的输入数据集的默认参数值。
最大值
最大值参数控制逻辑衰减的终点。 最大值越小,优先级在此函数主要衰减部分的下降速度越快(曲线越陡)。
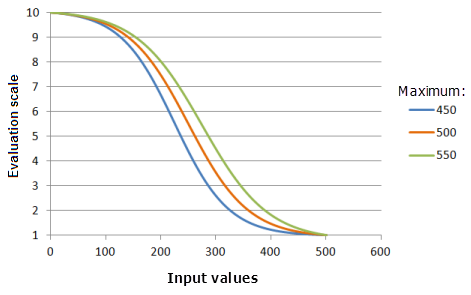
上图中使用的函数:
- TfLogisticDecay(0, Maximum, 99, 0, 1, 500, 10)
其中 Maximum 使用的值为 450、500 和 550。 最小值 0、最大值 500 和 y 截距百分比 99 是范围为 0 到 500 的输入数据集的默认参数值。
Y 截距百分比
Y 截距百分比参数确定逻辑衰减曲线衰减部分的值范围。 从概念上,将逻辑衰减函数视为反向的“S”形。 两条尾部由“S”的主体连接,这称为曲线的衰减部分。 此参数的值越大,则曲线衰减部分中包含的输入值范围越小(“S”越靠向垂直方向),但是这些值的优先级下降得也越快,曲线也会越明显。
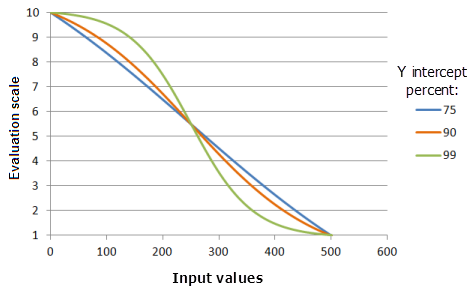
上图中使用的函数:
- TfLogisticDecay(0, 500, YInterceptPercent, 0, 1, 500, 10)
其中 Y 截距百分比使用的值为:75、90 和 99。 最小值 0、最大值 500 和 y 截距百分比 99 是范围为 0 到 500 的输入数据集的默认参数值。
逻辑增长函数
概览
逻辑增长变换函数类似于逻辑衰减变换函数,两者区别在于对数增长函数中的优先级会升高而非降低。
用例
在栖息地适宜性模型中,动物的优先级随着可用食物的增加而在逻辑上增加。 食物量必须先达到生存的临界水平,然后优先级会随食物增多而快速升高直至达到最大摄入量,此时优先级的提升速度会逐渐减缓。
参数作用
最小值
最小值参数控制逻辑增长的起点。 最小值越大,优先级在此函数主要增长部分的提升速度越快(曲线越陡)。
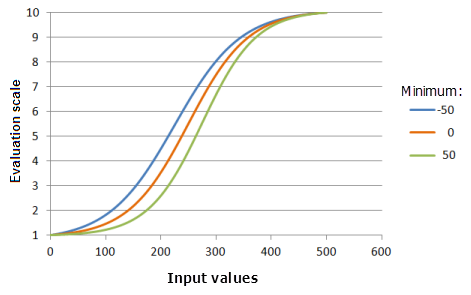
上图中使用的函数:
- TfLogisticGrowth(Minimum, 500, 1, 0, 1, 500, 10)
其中 Minimum 使用的值为 -50、0 和 50。 最小值 0、最大值 500 和 y 截距百分比 1 是范围为 0 到 500 的输入数据集的默认参数值。
最大值
最大值参数控制逻辑增长的终点。 最大值越小,优先级在此函数主要增长部分的提升速度越快(曲线越陡)。
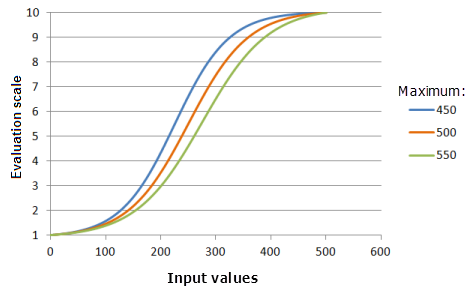
上图中使用的函数:
- TfLogisticGrowth(0, Maximum, 1, 0, 1, 500, 10)
其中 Maximum 使用的值为 450、500 和 550。 最小值 0、最大值 500 和 y 截距百分比 1 是范围为 0 到 500 的输入数据集的默认计算参数值。
Y 截距百分比
Y 截距百分比参数确定逻辑增长曲线增长部分的值范围。 从概念上,将逻辑增长函数视为“S”形。 两条尾部由“S”的主体连接,这称为曲线的增长部分。 y 截距百分比越小,曲线增长部分中包含的输入值范围越小("S" 越靠向垂直方向),但是这些值的优先级提升得也越快,曲线也会越明显。
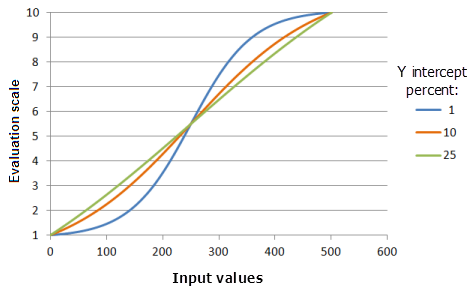
上图中使用的函数:
- TfLogisticGrowth(0, 500, YInterceptPercent, 0, 1, 500, 10)
其中 Y 截距百分比使用的值为:1、10 和 25。 最小值 0、最大值 500 和 y 截距百分比 1 是范围为 0 到 500 的输入数据集的默认参数值。
MS 大值 (MSLarge) 函数
概览
MS 大值变换函数与大值变换函数相似,只是此函数的定义是以指定平均值乘数和标准差乘数为基础的。 笼统地说,这两个函数间的区别在于 MS 大值 (MSLarge) 函数在极大值优先级较高的情况下更为适用。
如果采用特定的平均值乘数和标准差乘数组合,所得结果可能与大值变换函数非常类似。
用例
本用例与大值变换函数用例中所述的商品贸易适用性模型相似,只是此时咖啡产量较大位置的优先级的提升速度大大加快。
参数作用
平均值乘数
平均值乘数参数控制此函数曲线的坡度。 在此乘数降低时,较大值的适用范围会增大,而对于较大值,此函数曲线向阈值上限提升的速度将有所降低。
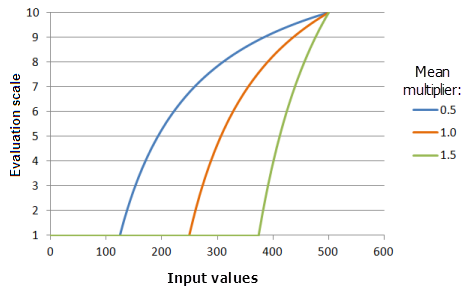
上图中使用的函数:
- TfMSLarge(MeanMultiplier, 1, 0, 1, 500, 10)
其中平均值使用的值为 0.5、1.0 和 1.5。 平均值乘数 1 和标准差乘数 1 是范围为 0 到 500 的输入数据集的默认参数值。
标准差乘数
标准差乘数参数用于控制此函数曲线的坡度。 随着该倍数的增加,函数曲线的提升速度会逐渐减缓。
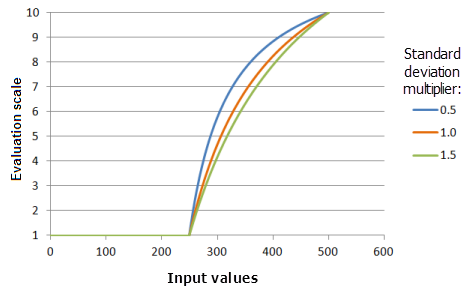
上图中使用的函数:
- TfMSLarge(1, StandardDeviationMultiplier, 0, 1, 500, 10)
其中标准差使用的值为 0.5、1.0 和 1.5。 平均值乘数 1 和标准差乘数 1 是范围为 0 到 500 的输入数据集的默认参数值。
MS 小值 (MSSmall) 函数
概览
MS 小值变换函数与小值变换函数相似,只不过此函数的定义是以指定平均值乘数和标准差乘数为基础的。 笼统地说,这两个函数间的区别在于 MS 小值 (MSSmall) 函数在极小值优先级较高的情况下更为适用。
如果采用特定的平均值乘数和标准差乘数组合,所得结果可能与小值变换函数非常类似。
用例
本用例与小值变换函数中所述的房屋适用性模型中针对建造成本条件而重设距公路距离的等级相似,只是此时较近像元位置的优先级的提升速度大大加快。
参数作用
平均值乘数
平均值乘数:用于控制此函数曲线的坡度。 在此乘数增加时,较小值的适用范围会增大,而对于较大值,此函数曲线向阈值上限下降的速度将有所加快。
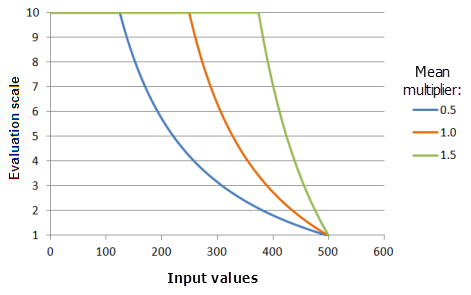
上图中使用的函数:
- TfMSSmall(MeanMultiplier, 1, 0, 1, 500, 10)
其中平均值使用的值为 0.5、1.0 和 1.5。 平均值乘数 1 和标准差乘数 1 是范围为 0 到 500 的输入数据集的默认参数值。
标准差乘数
标准差乘数参数用于控制此函数曲线的坡度。 随着此乘数的增加,函数曲线的下降速度会逐渐减缓。
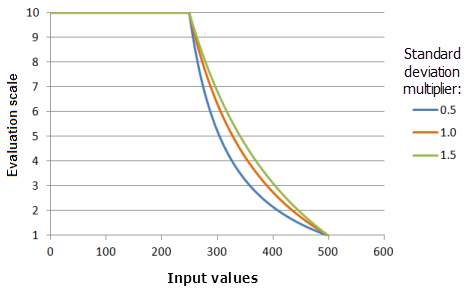
上图中使用的函数:
- TfMSSmall(1, StandardDeviationMultiplier, 0, 1, 500, 10)
其中标准差使用的值为 0.5、1.0 和 1.5。 平均值乘数 1 和标准差乘数 1 是范围为 0 到 500 的输入数据集的默认参数值。
近邻函数
概览
近邻变换函数最合适在接近特定值时优先级最高的情况下使用。 如果该中点介于阈值下限和阈值上限之间,则为至等级值分配一个等于中点的输入值。 其余输入值将从两个方向远离中点,因此它们的评估等级会降低(优先级降低),直至达到自等级值为止。
“近邻”和“高斯”变换函数可能相似,具体取决于指定的参数。 “近邻”函数通常比“高斯”函数以更快的速度递减,并且具有更窄的分布。 因此,它通常在值非常接近中点时优先级较高的情况下使用。
用例
本实例与高斯变换函数中所述的太阳能面板适用性模型相似,只是朝南的优先级的提升速度大大加快。
参数作用
中点
中点:与高斯函数的中点相同,可定义函数曲线的中心。
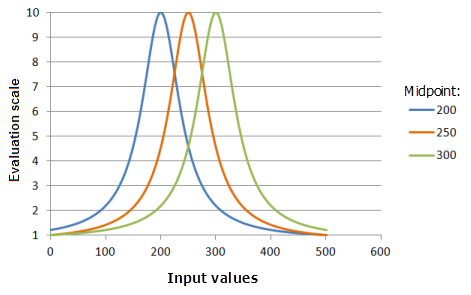
上图中使用的函数:
- TfNear(Midpoint, 0.000576, 0, 1, 500, 10)
其中 Midpoint 使用的值为 200、250 和 300。 中点 250 和散度 0.000576 是范围为 0 到 500 的输入数据集的默认计算参数值。
散度
散度参数类似于高斯函数,只是输入值远离中点会使优先级的变化更为急剧。
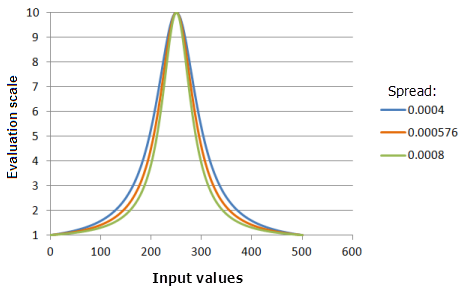
上图中使用的函数:
- TfNear(250, Spread, 0, 1, 500, 10)
其中 Spread 使用的值为 0.0004、0.000576 和 0.008。 中点 250 和散度 0.000576 是范围为 0 到 500 的输入数据集的默认计算参数值。
幂函数
概览
幂变换函数会使用已定义的平移对用于指定指数的输入数据应用幂函数。 在适用性模型中幂函数最适用的情况是:最小输入值的优先级最低,但优先级随输入值的增大而逐渐提升直至输入值达到较大值,此时优先级将快速升高(此行为取决于指数)。
用例
在用于定位核电站的适宜性模型中,要重设安全条件的与断层间距离的等级。 随着位置与断层线间距离的增大,其优先级将按幂函数方式持续提升,也就是说,距断层线较远的位置所具有的优先级远远高于距断层较近的位置。
参数作用
平移
平移参数是要从输入值中减去的值,可控制幂计算的起始输入值。 例如,在核电站用例中,已确定不应在距离断层线 10 千米的范围内建造核电站。 您可能希望对此幂函数进行平移,使其起始输入值为 10 千米。
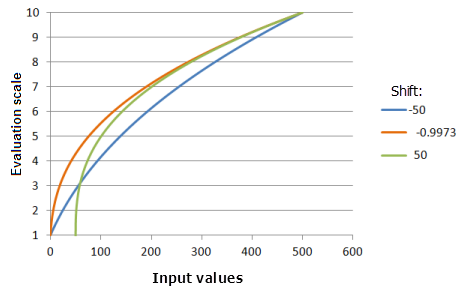
上图中使用的函数:
- TfPower(Shift, 0.3704, 0, 1, 500, 10)
其中 Shift 使用的值为 -50.0、-0.9973 和 50.0。 平移 -0.9973 和指数 0.3704 是范围为 0 到 500 的输入数据集的默认计算参数值。
指数
指数参数控制幂函数值增长的急剧程度。 指数越大,则函数曲线越陡,尤其是在输入值较大时。
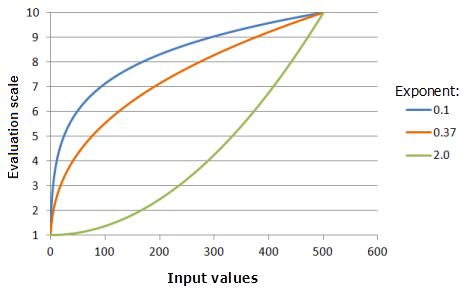
上图中使用的输入参数:
- TfPower(-0.9973, Exponent, 0, 1, 500, 10)
其中 Exponent 使用的值为 0.1、0.37 和 2.0。 平移 -0.9973 和指数 0.3704 是范围为 0 到 500 的输入数据集的默认计算参数值。
小值 (Small) 函数
概览
小值变换函数用于输入值越小优先级越高的情况。 已定义的中点用于标识函数的过渡点。 大于中点的值具有较低的优先级,小于中点的值具有较高的优先级。 值随着远离中点而增加和减小的速度由散度形状控制参数确定。
用例
在房屋适宜性模型中,您可能希望根据施工成本条件重设到道路的距离数据集的等级。 较接近公路的位置(小值)具有最高优先级(成本最低),优先级的值随距公路距离的扩大而持续下降。
参数作用
中点
中点:定义函数的过渡点。 将过渡点平移至大于输入数据中点的位置会更改过渡点,使得中点左侧优先级较高的较小值的范围增大,优先级的提升速度也会减慢。
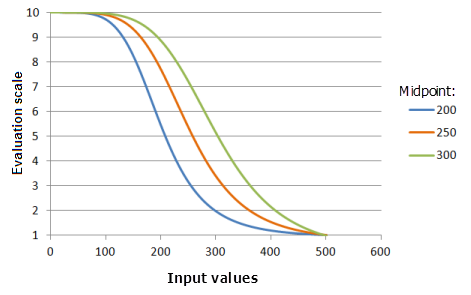
上图中使用的函数:
- TfSmall(Midpoint, 5, 0, 1, 500, 10)
其中 Midpoint 使用的值为 200、250 和 300。 中点 250 和散度 5 是范围为 0 到 500 的输入数据集的默认参数值。
散度
散度:控制优先级降低和升高的速度。 在散度值增大时,小于中点的输入值的优先级会更快升高,直至达到阈值下限;大于中点的输入值的优先级会更快下降,直至达到阈值上限
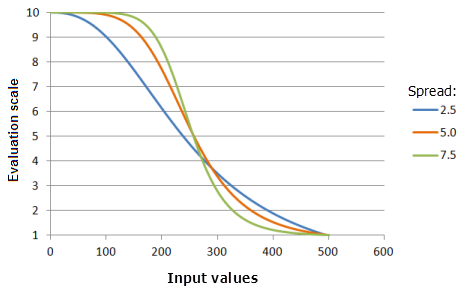
上图中使用的函数:
- TfSmall(250, Spread, 0, 1, 500, 10)
其中 Spread 使用的值为 2.5、5.0 和 7.5。 中点 250 和散度 5 是范围为 0 到 500 的输入数据集的默认参数值。
对称线性函数
概览
对称线性变换函数将在指定的最小值和最大值之间应用线性函数,该函数在最小值和最大值中点两边相对称。 镜像点的相应输入值将获得最高优先级值,随着输入值从镜像点移动,其优先级线性降低。 低于最小值但高于阈值下限或者高于最大值但低于阈值上限的任何输入值都将分配到自等级。
如果最小值大于最大值,则建立负线性关系(负坡度)。
对称线性函数最适用的情况是:中点值的优先级最高,并且优先级会随着输入值远离中点而以线性方式升高或降低。
用例
一种携带特定疾病的昆虫在 70 华氏度时最不活跃。 随着平均温度升高或降低到研究地点内的最低和最高平均温度,该昆虫将更加活跃,由此导致出现更多人类疾病病例。 为地区休闲设施选址时,平均温度为 70 度的区域具有最高优先级,并且优先级将随着温度由 70 度升高和降低以线性方式下降,直至温度达到研究区域的最高和最低平均温度。
参数作用
最小值
最小值参数可建立对称线性函数必须经过的某一个点。 更改最小值可能会更改函数镜像位置的中点。 您可能希望根据相应条件将最小值更改为输入栅格最小值以外的值,使该值与相关现象的优先级相对应。
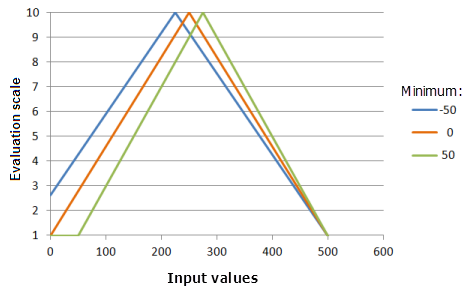
上图中使用的函数:
- TfSymmetricLinear(Minimum, 500, 0, 1, 500, 10)
其中 Minimum 使用的值为 -50、0 和 50。 最小值 0 和最大值 500 是范围为 0 到 500 的输入数据集的默认参数值。
最大值
最大值:建立对称线性函数必须经过的第二个点。 更改最大值可能会更改函数镜像位置的中点。 您可能希望根据相应条件将最大值更改为输入栅格最大值以外的值,使该值与相关现象的优先级相对应。
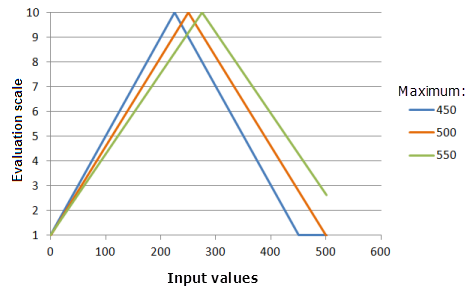
上图中使用的函数:
- TfSymmetricLinear(0, Maximum, 0, 1, 500, 10)
其中 Maximum 使用的值为 450、500 和 550。 最小值 0 和最大值 500 是范围为 0 到 500 的输入数据集的默认参数值。