派生连续流的工作原理

了解降水如何穿过景观对于许多应用程序来说都是至关重要的。 数字高程模型 (DEM) 是表面流建模的基础数据集。 然而，该数据并不是完美表示，它通常存在较小高程误差或景观要素的错误表示，这可能会影响流量。

因此，您必须在确定流向之前对输入 DEM 进行预处理。 水力调节是指修改输入 DEM 高程值以确保连续表面流可以代表实际表面流的练习。 要解决 DEM 限制破坏流网络的问题，必须使用水力调节，例如，伪高程可以充当汇，人为地积累和终止流动，从而导致无法确定从汇像元向外的流向。 不包括在表面模型中的桥梁、水坝和涵洞也可能产生错误的流向和流量输出。

工具通过应用最小成本路径算法（而非修改输入 DEM 数据方法）解决了错误的流向和流量输出问题。 最小成本路径算法涉及最小化跨输入表面栅格上坡移动的高程差。 换句话说，在逐个像元的基础上，需要一个优化步骤来识别最小上坡相邻像元。 此外，还应用了汇像元和 NoData 像元的特殊规则。 汇或洼地像元可以是单个像元或一组像元，其相邻像元的高程值高于处理像元或一组像元的高程值。 NoData 像元被认为是未知信息位置，不用于处理。

该工具使用 DEM 表面作为输入，并创建一个栅格来显示每个像元的流向和流量。

如果输入表面栅格包含实际汇或洼地区域，则应使用输入栅格或要素洼地数据参数对其进行指定。 如果指定了栅格数据集，则输入栅格中包含数据的像元将被视为有效的洼地像元。 如果指定了要素数据集，则要素将栅格化为与输入表面数据相同的分辨率，并且生成的栅格将用于指定有效的洼地像元。

该工具提供了两种使用流向类型参数确定流向的方法：D8 方法对从每个像元到其最陡下坡相邻像元的流向建模，并且仅限于单一方向（Jenson 和 Domingue，1988 年）。 MFD（多流向）方法允许使用根据当地地形条件调整流分区指数的方法跨所有下坡相邻像元进行流分区（Qin 等人， 2007 年）。

当指定输入累积权重栅格时，在导出累积时将权重应用于每个像元。

计算流向和流量

在派生连续流算法中，应用于流路径的最低成本路径方法包括两个基本步骤。 首先，设置有效的出口。 有效出口是水可以流入但不能流出的像元。 默认情况下，出口像元是输入表面栅格边缘的像元。 如果指定了输入栅格或要素洼地数据，则输入栅格或要素数据集中的像元也将在算法开始时被标记为有效出口。 第二步是遍历输入的表面栅格，通过按从最低高程到最高高程的顺序处理像元，得出每个像元的流向和流量。 这两个原则允许从当前单元格沿最陡上坡方向移动到下一个更高的像元（Metz 等人， 2011 年；Ehlschlaeger，1989 年）。

下图显示了遵循的常规逻辑。 有关未通过输入栅格或洼地数据参数和 NoData 明确指定为洼地的洼地（汇）像元等特殊情况，在处理未知洼地像元和输入表面栅格中的 NoData 像元部分中分别进行了说明。

图 1。 用于确定流路径和流量的最低成本路径算法（Metz 等人， 2011 年；Ehlschlaeger，1989 年）。

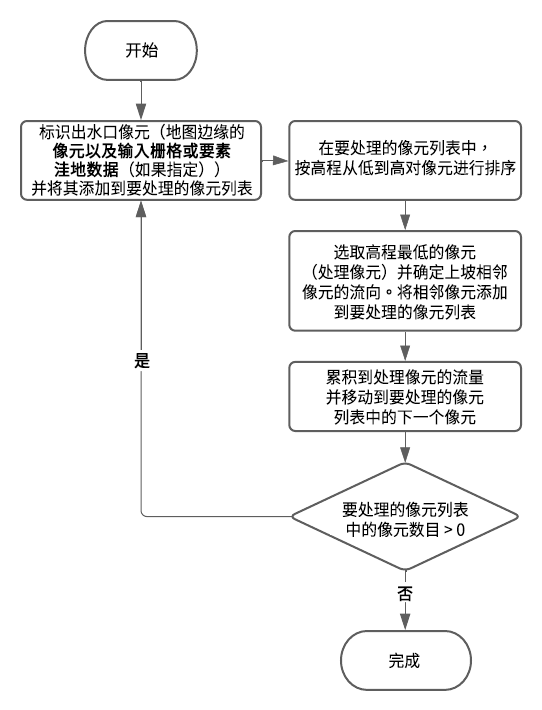
派生连续流逻辑

在本部分中，您将逐步了解派生连续流工具如何逐个像元处理高程数据并确定流向和流量的示例。 此示例演示了在可选输入栅格或要素洼地数据参数中未包含洼地的情况下的处理过程（请参阅图 2）。

图 2。 显示了像元大小等于 1 的合成高程数据示例。 此示例在表面栅格的中间区域附近有一个洼地，以黄色显示，该洼地未在输入栅格或洼地要素数据参数中指定。

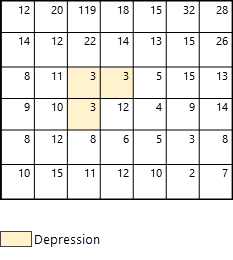
首先，识别出口。 这些对应于地图边缘的像元（在图 3 中以蓝色显示）。

图 3。 显示了在步骤 1 中识别为潜在出口的出口候选像元。

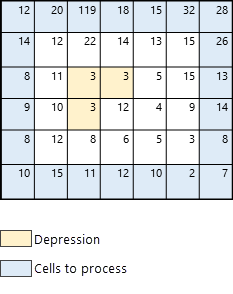
确定出口像元（蓝色像元）后，算法将从该像元开始继续寻找具有最低高程的像元。 在此示例中，最低像元（高程 2）在图 4 中以粗黑色边框突出显示。

图 4。 在步骤 2 中，通过按高程对潜在出口像元进行排序并选择高程最低的出口像元来确定起点，并以粗黑色边框突出显示。

下一步是识别处理像元（绿色）相邻像元中高程值大于处理像元的像元。 这些相邻像元将被添加到接接下来可能处理的像元中，如图 5 所示。 下一个要处理的像元是通过查找与最小上坡方向（图 5 中的蓝色箭头）相对应的最低高程上坡相邻像元（在本例中，高程值为 3 的像元）来确定的。 按处理像元顺序计算相邻上坡像元的流向和流量。 流向是使用流向类型参数中指定的方法确定的。 提供了两种可用于确定流向的方法：D8 和 MFD。 有关这两种方法的详细说明，请参阅下面的流向方法部分。

图 5。 在步骤 3 中，已识别当前处理像元的相邻像元。 以蓝色突出显示的像元是接下来可能要处理的像元。 黑色箭头对应流向，蓝色箭头对应处理路径。

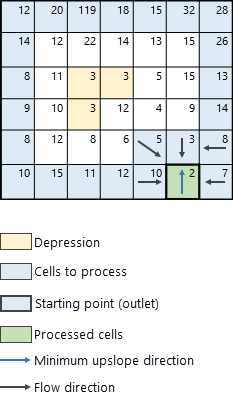
该算法以相同的方式继续，按照最小上坡的方向识别当前处理像元的相邻像元。 算法的下一次迭代如图 6 所示。

图 6。 显示下一次迭代。 在图 5 中，以蓝色突出显示的像元是接下来可能要处理的像元。 此逻辑示意图中要处理的下一个像元为 3，颜色为绿色。 黑色箭头对应流向，蓝色箭头对应最低成本路径方向。

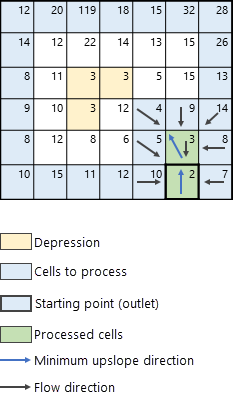
处理未知的洼地像元

洼地（或汇）像元可以是单个像元或一组像元，其相邻像元的高程值高于处理像元或一组像元的高程值。 如果这些不包括在输入栅格或要素洼地数据参数中，则它们将是工具的未知洼地像元。 在这种情况下，如果遇到一个未知的洼地像元或像元组，则路径将沿最陡坡降（而非沿最低上坡相邻像元）直到到达洼地的底部，从而确定沿洼地路径的流向和流量。 这个过程如图 7 所示。

图 7。 显示了处理洼地中每个像元的顺序（从左到右）。 流向和流量是在处理洼地内的每个像元时确定的。 通过洼地的处理方向是朝着最峭坡降方向，而不是沿最低的上坡相邻像元的方向。

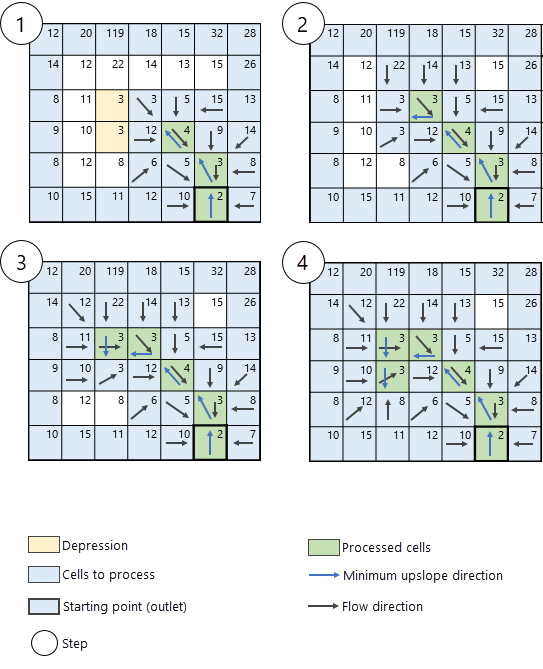
输入表面栅格中的 NoData 像元

输入表面栅格中的 NoData 像元是其值未知的像元。 这些像元可以存在于表面栅格中，并且可以在派生连续流算法期间遇到。 如果是这种情况，算法会绕过它们并不会对其进行处理，如图 8 所示。

图 8。 派生连续流工具会忽略输入表面栅格中的 NoData 像元。 外部 NoData 像元将输入表面栅格边界推送到具有有效数据值的相邻像元。 确定流向和流量的其余计算保持不变。

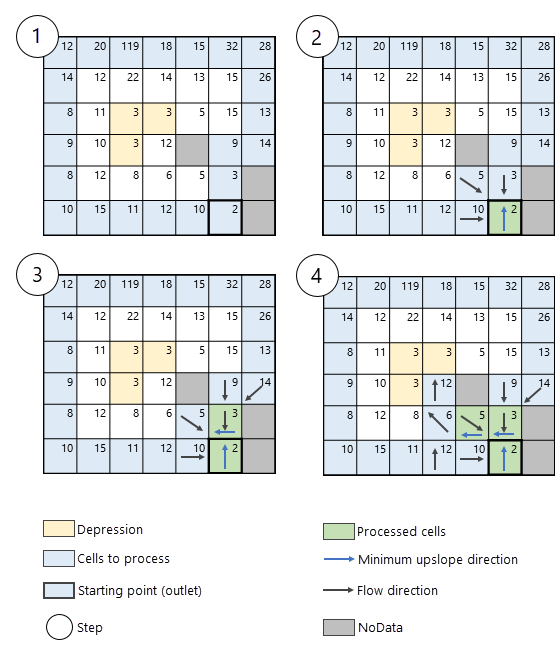
流向方法

在 D8 方法中，流向取决于自每个像元的最陡下降方向或最大下降高度（Jenson 和 Domingue，1988 年）。 流向计算如下：

maximum_drop = change_in_z-value/distance

将计算像元中心之间的距离。 对于拐角相邻像元，算法将验证朝向当前处理像元的最大下降高度是否为最大值；否则，流向将设置为朝向具有给定拐角相邻像元的最大下降高度的像元。 如果像元的 z 值在多个方向上均发生相同变化，则 D8 流向未定义，值将为可能方向的总和。

找到最陡下降方向后，将使用表示该方向的值对输出像元进行编码。

在 MFD 方法中，流将跨所有下坡相邻像元分区（Qin 等， 2007）。 每个下坡相邻像元接收的流量将估计为与最大坡度梯度的函数，其中考虑了局部地形条件。 用于估计 MFD 的表达式如下所示：

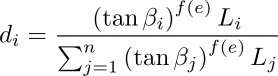
其中：

• d_i = 每个像元中流入像元 i 的流部分。
• f (e) = 根据局部地形条件调整的指数，给定如下：

  

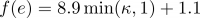
• β = 下坡角度（以弧度为单位）
• n = 流入像元 i 的像元数
• L_i, L_j = 用于考虑处理像元与正交和斜交像元的间距的调整系数
• κ = 流入像元 i 所有像元的最大下降高度

确定了流向、流量，以及最小成本路径的方向后，处理像元被标记为已处理，并分析队列中的下一个像元。 该算法以这种方式继续进行，直到输入表面栅格中的所有像元都已处理完毕。 或者说，直到已确定所有像元的流向和流量。

参考资料

Ehlschlaeger, C. R. 1989. "Using the AT Search Algorithm to Develop Hydrologic Models from Digital Elevation Data." International Geographic Information Systems (IGIS) Symposium 89: 275-281.

Jenson, S. K., and Domingue, J. O. 1988. "Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis." Photogrammetric Engineering and Remote Sensing 54 (11): 1593–1600.

Metz, M., Mitasova, H., & Harmon, R. S. 2011. "Efficient extraction of drainage networks from massive, radar-based elevation models with least cost path search." Hydrology and Earth System Sciences 15(2): 667-678.

Qin, C., Zhu, A. X., Pei, T., Li, B., Zhou, C., & Yang, L. 2007. "An adaptive approach to selecting a flow partition exponent for a multiple flow direction algorithm." International Journal of Geographical Information Science 21(4): 443-458.