可以使用最佳区域连接、最佳路径为线和最佳路径为栅格工具以最佳方式将位置与路径连接在一起。 但是,您可能希望结果不仅限于狭窄的折线或宽度为一个像元的路径。 您需要一个更大的二维区域,其中位置之间的总行进成本低于特定阈值。 该区域称为廊道。
可通过以固定距离对最佳路径进行缓冲来产生区域。 但是,这种方法可能无法正确捕获对行进者重要的信息。 例如,最佳路径周围的简单缓冲区可能包括工业园区,如果您正在规划野生动物廊道,则不适合包含该园区。 连接位置的廊道的宽度应能够根据位置之间各个像元之间实际累积成本的变化比率而变化。 由于对于野生动物而言,工业园区的成本非常高,因此该区域不会包括在廊道中。

廊道包含所有小于指定的累积成本的可能成本路径。 要定义廊道,最小成本廊道工具将源之间的每个像元累积成本栅格相加,并选择那些小于指定成本阈值的像元。
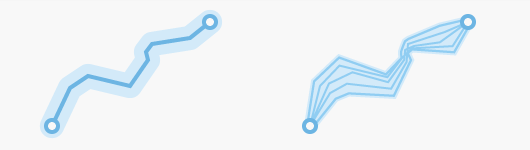
廊道计算示例
廊道可用于解决各种情况的分析,例如:
- 在养鹿计划中,将两片鹿栖息地与最佳廊道连接起来。
- 标识拟建地下管道的可能路径。
- 确定在连接两个公园时必须保留拟建自行车道的可行区域。
廊道分析
可以在概念上将距离分析分为以下相关功能领域:
- 计算直线距离,可以选择性地使用障碍或表面栅格调整计算。
- 可以选择使用成本表面、源特征、垂直系数和水平系数来确定遇到距离的比率。 创建累积距离栅格。
- 通过最佳网络、特定路径或廊道连接生成的累积距离表面的区域。
从第三个功能区开始,位置与廊道相连,如以下示例所示。
在新建的公园(浅绿色面)中存在一个熊种群,在四个管理站之一(黄色点)附近的周边区域存在第二个种群。 廊道将允许熊在两个位置之间移动。
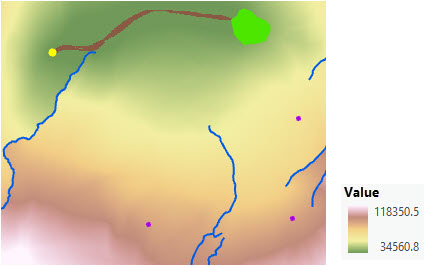
两个累积成本距离栅格和两个反向栅格是使用距离累积工具使用成本表面、溪流作为障碍(蓝线)和表面栅格创建的。 这四个栅格被输入到最小成本廊道工具中,并指定了一个阈值来定义廊道的宽度。
创建廊道
标识两个源之间的廊道的一般过程如下:
- 计算从第一个源位置到研究区域中每个其他像元的累积距离和反向。
- 计算从第二个源位置到研究区域中每个其他像元的累积距离和反向。
- 计算每个像元在两个源之间的累积距离的总和。
- 标识两个源之间的总累积距离位于定义的阈值内的像元。
要创建廊道结果,请完成以下步骤:
计算第一个源的距离累积和反向。
- 打开距离累积工具。
- 在输入栅格或要素源数据参数中提供要作为源(源 1)连接的第一个位置。
- 为源 B1 的输出距离栅格命名。
- 在输入成本栅格参数中标识成本栅格。
行进者的方向不能包含在廊道中。 因此,请勿指定垂直系数、水平系数或行进方向源特征参数的值。
- 为输出反向栅格命名。
- 单击运行。
- 打开距离累积工具。
- 在输入栅格或要素源数据参数中提供要作为源(源 2)连接的第二个位置。
- 为源 2 的输出距离栅格命名。
- 指定与在步骤 4 中指定的参数相同的参数。
- 为输出反向栅格命名。
- 单击运行。
- 打开最小成本廊道工具。
- 将在步骤 6 中创建的第一个位置(源 1)的输出累积距离栅格识别为输入累积成本距离栅格 1 参数值。
- 将在步骤 6 中创建的第一个位置(源 1)的输出反向栅格识别为输入反向栅格 1 参数值。
- 将在步骤 12 中创建的第二个位置(源 2)的输出累积距离栅格识别为输入累积成本距离栅格 2 参数值。
- 将在步骤 12 中创建的第二个位置(源 2)的输出反向栅格识别为输入反向栅格 2 参数值。
- 为输出廊道栅格命名。
- 指定阈值方法。 选择无阈值、最低成本百分比或累积成本。
- 如果选择最低成本百分比或累积成本作为阈值方法,请指定将用于定义廊道宽度的百分比或累积成本阈值。
- 单击运行。
使用最小成本廊道连接位置
廊道可定义连接两个源位置的最低成本地理区域。 其包含源之间所有小于指定累积成本的无方向成本路径。 廊道和其中的路径无方向,原因在于在源之间移动的方式无关紧要。
廊道创建过程
要创建廊道栅格,您需要四个数据集:两个定义到第一个源位置的距离要素,另外两个定义到第二个位置的距离要素。 您将使用距离累积工具为第一组源创建累积成本栅格和反向栅格。 然后使用相同的工具为第二组位置创建累积成本栅格和反向栅格。 使用这两个结果作为最小成本廊道工具的输入,该工具创建两个源之间的累计成本总和,并可选择应用阈值。 只有落在该阈值内的像元才会被选中以创建最终的廊道栅格结果。
设置一个阈值
设置阈值的方法有三种:无阈值、最低成本百分比和累计成本。
指定无阈值选项时,生成的廊道包含两个输入累积成本栅格相加的完整范围。
指定最低成本的百分比后,通过将指定的百分比应用于廊道曲面中的最小值来创建廊道。 如果指定的百分比为零或接近零,则某些像元可能会与廊道断开连接。 这些像元使用输入反向栅格连接到廊道。 有关其他信息,请参阅下面的廊道部分中断开连接的像元。
选择累计成本并指定阈值时,将选择累计成本等于或小于指定阈值的所有像元来创建廊道。 指定的阈值必须等于或大于廊道表面的最小值。 如果所选像元未在输入源之间创建连接的廊道,则它们将使用输入反向栅格进行连接。 有关详细信息,请参阅下面的廊道部分中断开连接的像元。
检查廊道
下图显示了为拟议电线项目创建的廊道示例。 评估廊道成本的唯一标准是土地购置成本。 最终廊道(浅红色)包含所有路径,这些路径的成本最多比从廊道表面的最小值导出的成本最低的路径高 10%,用深红色线显示。 廊道的宽度沿其长度变化,并且廊道在点处明显分叉。 此结果与在最低成本路径周围生成固定宽度缓冲区时的结果不同。
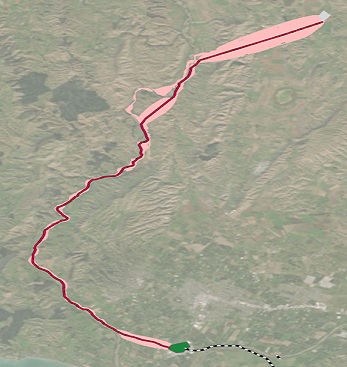
如果选择总累积成本最多比最低成本路径高 10% 的所有像元,则可将结果视为 10% 成本廊道。
廊道宽度
廊道的狭窄部分通常会标识廊道成本最敏感的区域,并且通过这些部分的路径的选择较少。 在电线案例中,廊道的较窄部分可能是应该首先购买的位置,原因在于在廊道的该部分中铺设电线时,纬度较小。 这些区域是廊道中最关键的位置。
当野生动物在廊道中逗留时,廊道的狭窄部分可能是野生动物在景观中移动时面临最大风险的位置。 这些狭窄的区域可能是最重要的保护区域,原因在于野生动物在廊道中移动时的选择将更少。
可视化廊道宽度重要性的另一种方法是考虑河流流经山谷。 在山谷宽阔且平坦的区域,河流通过该部分的方式可能有多种(阻力最小)。 发生洪水时,河流可能会溢出河岸并变宽,甚至路径会改变。 但是,在山谷变窄,最终成为峡谷,并且两侧都有陡峭围墙的区域,河流改变路径的几率很少。 可将峡谷狭窄部分周围的区域视为成本高得多的区域。 有关此概念的直观说明,请参阅下面的其他信息部分。 在可视化中,最低成本路径是河流,各种成本阈值是等值线。
适当阈值
阈值取决于成本表面的单位。 以美元为单位的成本是更容易定义的单位之一。 但是,对于野生动物廊道而言,如果成本单位为首选项,则确定阈值可能更具挑战性。 将生物阈值与主观首选项成本单位相关联将更加难以得到验证。
在这类案例中,尝试几个阈值,直到获得适当的宽度。 在理想情况下,指定的阈值将由客观测量决定。
廊道中的岛屿
根据指定的阈值,可在廊道分叉且之后重新连接的区域中生成的廊道中创建岛屿,例如上面的电线廊道示例。 岛屿像元的累积成本较高,并且廊道将在其周围导航。
廊道方向
廊道无方向,因此从一个源移动到另一个源与从第二个源移回第一个源的成本相同。 但是,在两次运行距离累积工具时,必须使用相同的设置,这一点很重要。
您可以使用成本表面和表面栅格来提高对距离进行建模的方式的复杂程度。 但是,您不能使用垂直系数、水平系数或行进方向源特征,原因在于这些参数取决于移动的方向性。
多个源位置
可用于创建输入累积成本栅格的唯一源的数量并不限于一个。 可以将多个源输入到距离累积工具中。 根据源之间的累积成本值和指定的阈值,可以在源之间生成多个廊道,而不是一个廊道。
在每个像元的基础上计算廊道
下图显示了如何为单个像元位置创建廊道。 对于输入栅格中的每个像元,此过程均会发生,但是出于演示目的,将显示一个像元。
要创建廊道,必须使用距离累积工具从源 1 创建累积成本栅格和反向栅格,并从源 2 创建累积成本栅格和反向栅格。
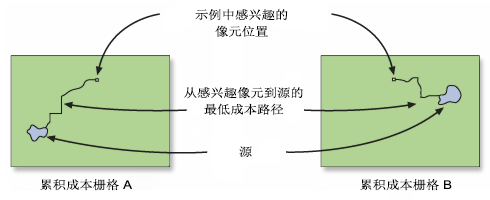
然后,最小成本廊道工具会将两个累积成本表面相加在一起。
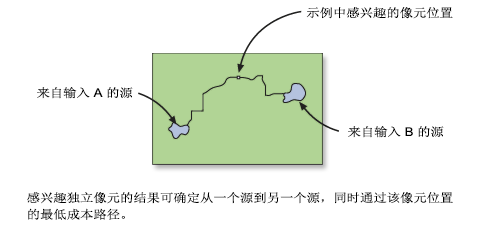
求和结果未在两个源之间定义一条最低成本路径。该栅格可标识源之间的累积成本范围。 也就是说,到达源 1 的最低累积成本加上到达源 2 的最低累积成本等于通过某个像元的路径的总累积成本。 如果从源 1 到源 2 的路径经过该像元,则该累积成本就是最低累积成本。
然后应用阈值以定义廊道的宽度。
从栅格中选择所有累积成本值小于指定阈值的像元以创建廊道。 应用阈值后,可将结果输出视为像元的最小成本廊道,而不是最低成本路径(单条线)。
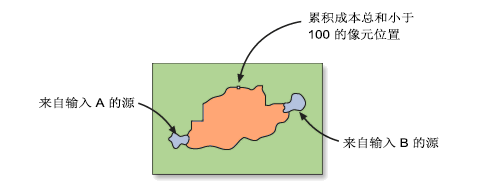
两个反向栅格用于确保廊道中没有断开连接的像元。 有关其他信息,请参阅下面的廊道部分中断开连接的像元。
解释廊道
廊道的宽度可能会沿其长度发生很大变化。 其不是最低成本路径周围的固定距离缓冲区。 您可以定义所需的最小宽度,并确定一组最低成本路径是否会形成可接受廊道。
考虑廊道的另一种方法是,廊道会显示最低成本路径位置的不确定性。 给定的最低成本路径周围的 10% 廊道是所有路径的良好且直观的汇总,这些路径的成本最多比最低成本路径高 10%。
廊道可以显示最低成本路径对其位置变化敏感的位置。 在上面的电线示例中,廊道顶部的较宽区域位于价格低廉的土地上,因此在未显著影响其成本的情况下,可采用多种方式更改路径在该区域中的位置。 相反,在狭窄的廊道中间部分中,替代最低成本路径在空间上受到限制,几乎无法对其进行更改。
其他信息
以下部分将提供有关通过廊道连接位置的其他信息。
成本不是欧氏距离累积
距离累积工具输出的距离累积栅格主要有两种类型:欧氏距离或成本距离。 仅输入源时,将创建距离累积栅格的欧氏距离版本。 距离累积栅格的成本距离版本通常是根据输入源和成本表面创建的。
如果将距离累积栅格的欧氏距离版本输入到最小成本廊道工具并指定了阈值,则结果将类似于在源之间的最短路径周围创建缓冲区。 最小成本廊道工具对于距离累积栅格的成本距离版本更为有效。 距离累积栅格的成本距离版本通常是根据输入源和成本表面创建的。 成本距离是成本在每个像元中出现的比例。 因此,廊道的宽度取决于您离开最低成本路径时遇到的情况。
廊道内断开连接的像元
创建廊道本质上是一次两步分析。
首先,距离累积工具计算到输出累积成本栅格中每个像元中心的最低成本距离。 要确定到每个像元的最低成本距离,将创建从成本最低的源到像元中心的最低成本路径。 路径的计算与栅格结构无关,使用距离累积工具中的数值计算方法。 在廊道分析中,特别重要的是源 1 和 2 之间理想的最低成本路径。 由于廊道中没有方向,源 1 和 2 之间以及源 2 和 1 之间的理想最低成本路径应该相同。
距离累积工具将两个源之间理想的最低成本路径映射到成本面定义的像元结构或在分析环境中设置的单元结构(以及所有最低成本路径)。 此栅格化过程中存在轻微畸变。
最小成本廊道工具采用两个输入累积成本栅格的总和,并根据廊道栅格中的最小值重新创建源 1 和源 2 之间理想的最低成本路径。 导出的理想最低成本路径是确定廊道的基础。 阈值确定了廊道的宽度,它与派生的理想最低成本路径相关。
任何落在指定阈值内的像元中心都将包含在廊道中。
注:
出于本节讨论的原因,由最小成本廊道工具确定的派生理想最低成本路径并不总是等于最佳路径为线工具实现的最低成本路径。
廊道有两个要求:
- 它必须连接两个输入源。
- 廊道中的所有像元必须是连续的。
但是,有三个因素可以挑战这两个要求:
- 像元大小。
- 计算中的微小变化。 靠近声源的畸变比远离声源的稍微显著一些。 这种微小的畸变会增加这些位置的累积成本,并且当将两个输入栅格加在一起时,畸变会稍微复杂化。
- 成本表面的可变性,特别是在成本高的地区。
由于这些相互作用的因素,有两种主要情况可以在廊道中创建断开连接的像元。 最小成本廊道工具可确保这些断开连接的像元在廊道内相连。
方案 1
在这种情况下,断开连接的像元发生在远离源的地方,在这些源中,计算的可变性导致的畸变较小,并且在具有高成本像元的区域中。
下面是黑熊野生动物廊道中断开连接的像元的示例。 廊道(蓝色区域)连接两个栖息地(紫色和黄色区域)。 廊道中间断开连接的像元(用箭头表示)位于高成本像元区域。 这些断开连接的像元将由最小成本廊道工具使用输入反向栅格自动连接。
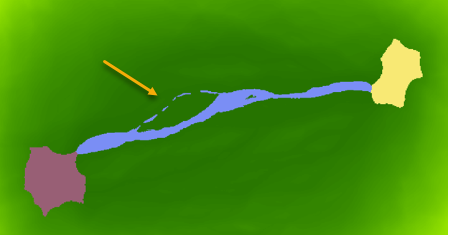
下图中的模拟示例最好地说明了像元断开连接的原因。 黑色区域是由指定阈值定义的所需廊道,相对于派生的理想最小成本路径,与廊道地图中的像元中心无关 - 两个累积成本图层的总和。

如前所述,距离累积会计算到每个像元中心。 在高成本区域,源 1 和 2 之间理想的最低成本路径将尝试限制高成本像元内的行程。 但是,可能需要穿过像元的一部分,例如拐角,避免累积到达像元中心的全部成本。
由阈值定义的所需廊道被映射(栅格化)回廊道栅格的栅格像元(使用像元中心方法)。 尽管廊道穿过高成本像元的一部分,但它不包括像元中心。 像元不会包含在廊道中。 结果,某些像元可能会与廊道断开连接。
但是,反向输入栅格知道如何导航通过这些成本较高的像元。 最小成本廊道工具使用这些栅格将断开连接的像元连接到廊道。 用于连接这些断开连接的像元的像元将具有比指定阈值略高的累积成本。
为减少这种畸变,在距离累积工具中创建距离累积栅格时可以使用较小的像元。 较小的像元可以捕获聚合到较粗的像元中的实际较低的累积成本,或者它将较粗的像元划分为较小的像元。 成本最低的路径可以通过这些更小、成本更低的像元,从而避免承受到达像元中心的全部成本。
方案二
在此方案下,当使用累积成本方法并将阈值设置为接近廊道表面的最小值(累积距离栅格 1 和 2 的总和)时,会创建断开连接的像元。 或者,可以使用最低成本百分比方法并将百分比设置为零。
在此方案下,最小成本廊道工具使用累积栅格总和的最小值导出两个源之间的理想最低成本路径。
导出的理想最低成本路径通过具有最低总和累积成本的一个或多个像元,可能通过像元中心。 如果成本最低的路径遇到成本较高的区域,则像元的累计成本总和将大于最小值,原因如上所述。 可能会导致像元断开连接。 使用反向栅格,最小成本廊道工具将确保两个源至少与一个像元廊道相连接。 用于连接断开连接像元的所有像元的累积成本将略高于阈值(廊道栅格中的最小值)。
下图说明了此场景的概化版本。 成本表面是一个包含所有 1 的模拟数据集。 连接两个源(粉红色方块)的派生最低成本路径显示为一条线。 使用 0% 阈值选择包含在廊道中的像元用黑色表示。 由于成本表面包含所有 1,因此导出的最低成本路径是一条直线。

廊道(黑色像元组)中出现间距,因为栅格化太过粗略。 最初不会选择连接的像元序列。 最小成本廊道工具将使用反向栅格连接像元,从而创建一条连续的廊道。
了解廊道
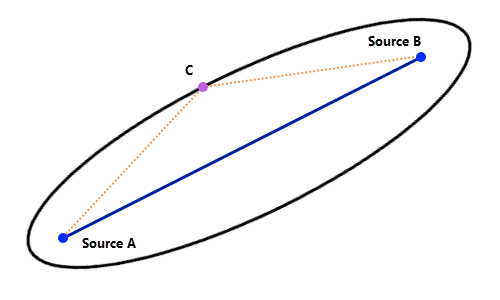
要了解为何添加两个距离累积栅格并设置阈值会创建廊道,请从最简单的几何案例开始。 直线是平面中两点间的最低成本路径。 如果点 C 位于该线上,则 AC + CB = AB。 廊道术语表明,从 C 到 A 和从 C 到 B 的累积成本总和是恒定的,并且也是最小值(AB 线的长度)。 因此,直线是 A 和 B 之间的 0% 廊道。 这也是创建最低成本路径的另一种方式,您无需使用反向栅格。
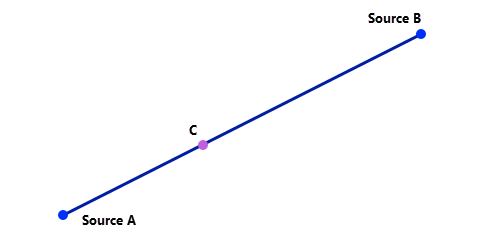
如果 C 移出线(远离最低成本路径),则 AC 是从 C 到 A 的新最低成本路径,而 CB 是从 C 到 B 的最低成本路径。 因此,AC + CB > AB。 具有相同总成本的所有点会在原始的最低成本路径周围形成椭圆。 将 C 连接到 A 和 B 的所有最低成本路径都包含在廊道中。 在廊道术语中,椭圆是最小成本路径周围的 x% 廊道。 与电线示例一样,在廊道的起点处,最低成本路径周围的最小成本廊道不同于该路径周围的固定宽度缓冲区。
当处理更通用的最低成本路径时,也存在这些情况。 0% 廊道与最低成本路径相同,而阈值较高的廊道会形成包含该走廊中的所有像元和所有路径的等值线环。
如果移动方向在您的最低成本路径分析中并不重要,则可以使用廊道可视化最低成本路径或可以定位替代无方向路径的所有位置的不确定性,这些位置位于最低成本路径的可接受成本阈值范围内。
可视化廊道
在 3D 模式下查看廊道时,您可以获取见解和视角。 最低成本路径成为由总累积成本输入表面构成的峡谷的相对水平的地面,并且各种 x% 廊道在峡谷壁上形成等值线。 从峡谷壁上的任何一点开始,您必须下坡才能到达源,这意味着您需要在等值线以下行进,该等值线指示您处于该百分比的廊道内。

电线示例中廊道的较宽部分包含在上图中较宽且较平的碗状区域中。 如果您愿意花费额外的累积成本,则可以提高阈值。 由于廊道的宽度会显着增加,因此较宽的碗状区域可为您提供更多规定路径的方法。 峡谷墙可显示哪方面的投资将不太成功。