多比例地理加权回归 (MGWR) 工具使用地理、城市规划和其他各种学科执行高级空间回归技术。 它从地理加权回归 (GWR) 模型演变而来,该模型使用目标要素邻域内的解释变量和因变量来构建用于解释或预测的局部线性回归模型。
使用 GWR 的主要动机是对大的地理区域使用单一回归模型可能限制太多。 相反,GWR 允许在每个空间位置使用不同的回归模型,回归系数在该区域平滑变化。 这意味着在研究区的不同位置,解释变量对因变量的影响是不同的。 GWR 通过使用要素及其空间邻域的解释变量和因变量为每个空间要素创建加权回归模型来实现这一点。 离要素越近的相邻要素获得的权重越高,对局部回归模型的影响就越大。
MGWR 是 GWR 的扩展,它允许每个空间要素周围的邻域在每个解释变量之间变化。 这意味着对于某些解释变量,邻域可以大于或小于其他变量。 允许不同的解释变量具有不同的邻域很重要,因为解释变量和因变量之间的关系可能在不同的空间尺度上起作用:一些变量的系数可能在整个研究区域逐渐变化,而其他变量的系数变化很快。 将每个解释变量的邻域与解释变量的空间尺度相匹配,使 MGWR 能够更准确地估计局部回归模型的系数。
MGWR 擅长处理包含至少数百个要素和数据集的大型数据集,其中因变量表现出空间异质性。 为了在较小的数据集中对空间变化的关系进行建模,其他工具可能更合适。 当前的多比例地理加权回归 (MGWR) 工具仅接受连续因变量。 不要使用二进制或计数数据运行模型。 这可能会导致偏差模型和无意义结果。
本主题的大部分内容将通过与其他回归方法比较来解释 MGWR。 在继续之前,对普通最小二乘 (OLS) 回归有一个基本的了解并熟悉 GWR 的邻域、加权方案和诊断将很有帮助。
回归模型选项
OLS、GWR 和 MGWR 都是线性回归模型,但它们在不同的空间比例上运行,并对数据集的空间异质性(研究区域内关系的一致性)做出不同的假设。 OLS 是一种全局模型。 假设数据生成过程在空间上是平稳的,因此单个系数可以解释每个解释变量和因变量之间的关系。 GWR 是一种局部模型,它通过允许系数随空间变化来放宽空间平稳性的假设。 然而,在 GWR 中,通过要求所有解释变量使用相同的邻域,假设所有局部关系在相同的空间比例上运行。 例如,如果一个解释变量使用 20 个相邻要素,则所有解释变量也必须使用 20 个相邻要素。
然而,MGWR 不仅允许系数随空间变化,而且允许比例随不同解释变量变化。 MGWR 通过为每个解释变量使用单独的邻域,说明每个解释变量和因变量之间关系的不同空间比例以做到这一点。 这样,可以将在相对较大的空间比例上运行的解释变量(例如温度或大气压力)与在较小空间比例上运行的变量(例如人口密度或收入中位数)结合起来。
与 GWR 相比,MGWR 可估计更准确的局部系数并且遇到的多重共线性问题更少。 但是,MGWR 的处理时间比 GWR 长得多,尤其是对于邻域选择方法参数的黄金搜索、手动间隔或用户定义选项。 这三种邻域选择方法都是基于计算和内存密集型的反向拟合算法。 随着数据大小的增加,运行时间和内存使用量会显着增加。
在决定将哪种模型应用于您的数据时,请考虑以下问题:
- 我的模型应该在局部还是全局级别运行?
- 如果您想要局部模型,请应用 GWR 或 MGWR。 否则,请使用 OLS 或其他模型,例如基于森林的分类和回归工具。
- 我的模型中的解释变量是否在不同的空间比例上运行?
- 如果您怀疑解释变量可能在不同的比例上运行,并且想对这些不同的比例进行识别和建模,请应用 MGWR。
- 我的数据集有多大? 我要等多久才能得到结果?
- 如果您的数据集非常大并且运行的是 MGWR 工具,工具执行应该会需要更长的时间。 如果使用 2020 年代初期的通用硬件(16 个逻辑处理器和 32 GB 内存)和典型参数,对于大于大约 10,000 个点的数据集,运行时间可能会是几个小时。 对于 50,000 个点的数据集,运行时间可能是几天。 对于 100,000 或更多点的数据集,可能会发生内存错误。
如果您仍然不确定将哪个本地模型(GWR 或 MGWR)应用于您的数据,请从 MGWR 开始。 当 MGWR 运行时,它也在特定设置下执行 GWR。 在地理处理消息中,您可以找到 GWR 诊断并将其与 MGWR 的诊断进行比较。 或者,您可以运行多个工具(OLS、GWR 和 MGWR)并使用地理处理消息中列出的 AICc 来比较模型并选择最佳模型。 如果您选择运行多个工具,请缩放所有模型或不缩放所有模型以确保输出具有可比性。
可能的应用
MGWR 可以应用于许多多变量分析和问题,例如:
- 房间数量、建造年份、地块面积等各种要素是如何影响房屋价格的? 不同社区的关系是否有显著差异?
- PM2.5 的分布与区域家庭收入、每户汽车数量或农业占国内生产总值百分比等经济变量有何关联?
- 在精准农业中,土壤条件对作物产量在空间比例上的影响是否与温度、湿度和降水等大气变量相同?
性能和基准注意事项
多种因素会影响 MGWR 的运行时间。 运行时最重要的因素是要素数量。 运行时间随着要素数量呈立方增长。 邻域大小和解释变量的数量也会影响 MGWR 的运行时间,因为每个局部模型需要更多的计算。 为了尽可能快地计算结果,MGWR 在您的计算机上采用并行处理。 一些计算将使用所有可用的内核,但其他计算可以由并行处理因子环境控制。
工具输入
有几种方法可以提供解释变量的空间比例。
邻域(带宽)选择
MGWR 的一个关键增强是能够改变线性回归方程中每个解释变量的带宽(邻域)。 目标位置的解释变量的邻域包括有助于估计局部线性回归模型中解释变量系数的所有位置。 每个邻域由目标要素周围的多个邻域或固定距离内的所有邻域定义。 每个解释变量的邻域数量或距离可能不同。
对于邻域选择方法参数,系统提供 4 个选项,可用于评估每个解释变量的最佳空间比例:
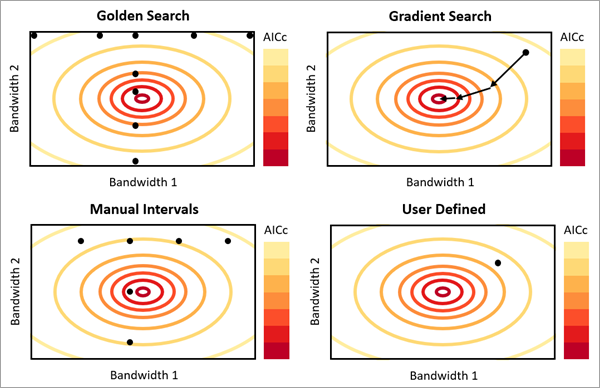
黄金搜索 - 可以使用黄金搜索算法确定每个解释变量的相邻要素的数目或距离范围。 此方法将在指定的最小值和最大值之间为每个解释变量搜索多个值组合。 该过程将迭代进行,并使用之前值的结果以选择要测试的每个新组合。 选择的最终值将具有最小的 AICc。 对于相邻要素的数目选项,可以使用最小相邻要素的数目和最大相邻要素的数目参数指定最小值和最大值。 对于距离范围选项,可以使用最小搜索距离和最大搜索距离参数指定最小值和最大值。 所有解释变量将共享最小值和最大值,但每个解释变量的估计相邻要素的数目或距离范围将不同(除非两个或多个巧合地具有相同的空间尺度)。 该选项花费的计算时间最长,尤其对于大型或高维数据集更是如此。
梯度搜索 - 使用基于梯度的优化算法确定每个解释变量的相邻要素的数目或距离范围。 为了确定每个解释变量的最佳带宽,梯度搜索将采用 AICc 相对于带宽的导数并更新带宽,直到确定最低 AICc 为止。 对于相邻要素的数目选项,可以使用最小相邻要素的数目和最大相邻要素的数目参数指定最小值和最大值。 对于距离范围选项,可以使用最小搜索距离和最大搜索距离参数指定最小值和最大值。 与黄金搜索一样,所有解释变量将共享最小值和最大值,但每个解释变量的估计相邻要素的数目或距离范围可能不同(除非两个或多个巧合地具有相同的空间尺度)。 此选项将评估与黄金搜索相当的邻域,但其具有更好的运行时性能,并且需要使用的内存量要少得多。
手动间隔 - 通过从最小值开始递增相邻要素的数目或距离范围来确定每个解释变量的相邻要素的数目或距离范围。 对于相邻要素的数目选项,该方法将从最小相邻要素的数目参数的值开始。 然后,相邻要素的数量会加上相邻要素的数目增量参数的值。 将重复相应次数的此增量,可以使用增量数参数指定该次数。 对于距离范围选项,该方法将使用最小搜索距离、搜索距离增量和增量数参数。 每个解释变量使用的相邻要素的数目或距离范围将为测试值之一,但每个解释变量的值可能不同。 此选项比黄金搜索更快,并且经常评估可比较的邻域。
用户定义 - 所有解释变量使用的相邻要素的数目或距离范围。 可以使用相邻要素的数目或距离范围参数指定该值。 如果已知最佳值,则此选项可提供最大程度的控制。
默认情况下,每种邻域选择方法的相关邻域参数适用于所有解释变量。 但是,可以使用邻域类型和选择方法的相应覆盖参数为特定解释变量提供自定义邻域选择参数:适用于黄金搜索的相邻要素的数目、适用于梯度搜索的相邻要素的数目、适用于手动间隔的相邻要素的数目、用户定义的相邻要素数目、适用于黄金搜索的搜索距离、适用于梯度搜索的搜索距离、适用于手动间隔的搜索距离或用户定义的搜索距离。 要针对特定解释变量使用自定义邻域,请在相应覆盖参数的第一列中提供解释变量,并在其他列中提供邻域的自定义选项。 这些列与其覆盖的参数具有相同名称;例如,如果您将手动间隔与距离范围配合使用,则搜索距离增量列将指定搜索距离增量参数的自定义值。 在地理处理窗格中,自定义邻域参数位于自定义邻域选项参数类别中。
例如,假设您使用 3 个具有 30 个最小相邻要素和 40 个最大相邻要素的黄金搜索邻域类型的解释变量。 如果该工具使用这些参数运行,则 3 个解释变量中的每个解释变量都将使用 30 到 40 个相邻要素。 如果您仅希望针对第二个解释变量使用 45 到 55 个相邻要素,则可以在适用于黄金搜索的相邻要素的数目参数的列中提供第二个解释变量、自定义最小值和自定义最大值。 使用这些参数,第一个和第三个解释变量将使用 30 到 40 个相邻要素,第二个解释变量将使用 45 到 55 个相邻要素。
局部权重方案
MGWR 通过对要素及其邻近要素应用地理加权(核)函数来估计每个目标要素的局部回归模型。 距离目标要素越近的邻近要素对局部模型的结果影响越大。 内核选项在局部加权方案参数中可用:高斯和双平方。 要了解有关使用核进行地理加权的更多信息,请参阅地理加权回归的工作原理。 在 MGWR 中,加权带宽根据解释变量而异。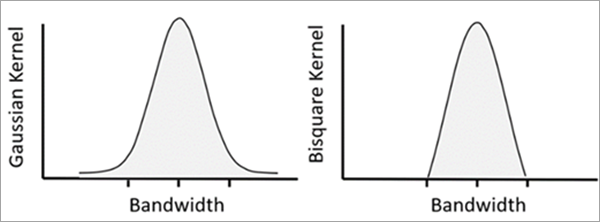
注:
梯度搜索邻域类型只支持使用双平方核。 未来版本可能会支持使用高斯核。
缩放的数据和系数
默认情况下,所有解释变量和因变量都被缩放为均值为零,标准差为 1(也称为 Z 分数标准化)。 缩放数据值的估计系数以标准偏差解释;例如,系数 1.2 意味着解释变量增加 1 个标准差,则因变量相应增加 1.2 个标准差。 因为所有系数都使用一个共享单位,所以可以直接比较这些值以查看哪些解释变量对模型的影响最大。 通常建议对变量进行缩放,当变量的取值范围变化很大时,缩放尤其重要。 但是,您可以通过取消选中缩放数据参数来选择不缩放数据。
在 OLS 和 GWR 等大多数线性回归模型中,线性缩放的系数是不变的。 这意味着如果您缩放输入数据、拟合回归模型、将结果重新缩放回原始单位后,结果将与未缩放前的数据相同。 然而,在 MGWR 中,缩放后再取消缩放,将不会产生从原始数据中接收到的相同模型。 这是因为反向拟合是一个迭代过程,其中每一步的结果取决于前一步的结果。 使用不同的起始比例会影响测试值的路径,并导致不同的 MGWR 模型。 缩放的结果通常最准确,因为缩放使变量的方差相等,并且当每个变量对数据的总方差贡献相等的量时,迭代过程通常会更快地收敛并获得更准确的值。 如果解释变量具有不同的方差(例如,包含不同的单位),则方差较大的变量对迭代估计每一步骤的影响更大。 在大多数情况下,这种影响会对模型的最终带宽和系数产生负面影响。
为了便于解释缩放结果,工具输出的所有系数都将包含缩放值和未缩放到原始数据单位的值。 这些输出包括输出要素上的额外字段(也作为图层添加到输出组图层)和输出系数栅格工作空间参数目录中的额外栅格。 使用预测位置和输出预测要素参数预测新位置时,所有预测值都未缩放为原始数据单元。 有关输出的更多信息,请参阅工具输出。
工具输出
该工具生成各种不同的输出,包括用于输出要素、消息和图表的各个字段的图层组。 可选输出包括预测新位置值的要素类、邻域表和每个系数的栅格表面。
图层组和符号系统
默认输出符号系统图层使用分类颜色方案可视化局部线性回归模型的标准化残差。 检查残差模式以确定模型是否指定完好。 明确指定的回归模型的残差将处于正态分布,并且在空间上是随机的没有值的聚类。 您可以对回归残差运行空间自相关 (Global Moran's I) 工具来测试是否在空间上随机。 统计上显著性高低残差聚类表明 MGWR 模型不是最优解。
每个解释变量的系数和统计显著性图层作为一个图层组添加到地图中,每个解释变量都有单独的子图层组。 每个图层的系数呈现出以零为中心的发散配色方案。 这允许您使用颜色来识别哪些变量与因变量具有正负关系。 对于点,具有统计显著性(95% 置信度)的要素由点周围的绿色光晕表示,不显著的关系由灰色光晕表示。 对于面,显著性关系用面中的纹理网格表示。 检查系数图层和显著性图层,以更好地了解解释变量的空间变化。 您可以利用从这种空间变化中获得的洞察力来制定政策。 当变量具有全局统计显著性并且显示出很小的区域差异时,全局策略可能会运作得更好,但当回归系数存在显着空间差异时,局部策略可能会运作得更好。 在这种情况下,在局部效应积极且较大的地区启动策略可能更合适。 然而,同样的策略可能不适用于其他影响较小或负面影响的领域。
消息和诊断
这些消息提供有关 MGWR 模型及其性能的信息。 消息分为几个部分。
系数估计的汇总统计
系数估计的汇总统计部分总结了整个研究区域内系数估计的平均值、标准差、最小值、中值和最大值。 每个系数的平均值反映了解释变量和因变量之间的关联。 标准差表示每个解释变量的空间变化。 小的标准偏差意味着更简单的方法(如 OLS)可以充分模拟数据。 如果选中缩放数据参数,您可以比较解释变量的值。 如果未勾选缩放数据参数,则无法直接比较解释变量之间的系数值,因为单位可能不同。
模型诊断
模型诊断部分包括一个表格,其中显示了 GWR 和 MGWR 的几个模型诊断,包括 R2、调整后的 R2、AICc、残差方差和有效自由度数。 有关这些模型诊断的更多详细信息,请参阅地理加权回归的工作原理。
注:
在某些情况下,用于比较的 GWR 模型可能无法计算。 在这种情况下,仅显示 MGWR 的诊断信息。
您可以使用 R2 和调整后的 R2 诊断来评估模型与数据的拟合优度。 R2 和调整后的 R2 越高,模型对数据的拟合越好。 通过解释变量的数量和有效自由度诊断来评估模型的复杂性。 更简单的模型具有更高的有效自由度和更少的参数。 如果模型的参数太多,则存在过度拟合数据的风险。 AICc 诊断说明了拟合优度和模型的复杂性。 多比例地理加权回归工具选择具有最低 AICc 的模型。
解释变量和相邻要素汇总
解释变量和邻域摘要部分显示每个解释变量的估计邻域和显著性水平。 对于基于相邻要素数量的邻域来说,最佳相邻要素数显示为计数和输入要素总数的百分比。 对于距离范围邻域,最佳距离范围与距离一起显示为输入要素对角线范围的百分比。 要素或范围的百分比对于描述解释变量的空间比例是有用的;例如,如果解释变量使用 75% 的要素作为相邻要素,则局部回归模型比局部模型更接近全局模型(表明更简单的模型,如 OLS 可能就足够了)。 如果另一个解释变量仅使用 5% 的输入要素作为相邻要素,则它是一个更局部的模型。 对于所有邻域类型,将针对每个解释变量显示在 95% 置信水平上具有统计显著性的局部模型的计数和百分比。
最佳带宽搜索历史
最佳带宽和搜索历史部分显示可能的最佳带宽的搜索历史以及每组测试值的 AICc 值。 该工具开始通过为每个变量分配相同的值来搜索每个解释变量的最佳带宽:GWR 的最佳带宽。 然后,该工具会在每次迭代中调整每个变量的带宽和系数并估计一个新的 AICc 值。 随着迭代的进行,AICc 值会减小,直到其保持稳定或增大时结束迭代。 用户自定义选项通常需要最少的迭代,而黄金搜索选项通常需要最多。 虽然它使用大量迭代,但梯度搜索选项通常具有最快的运行时间,因为每次迭代都可以快速计算。
注:
对于使用相邻要素数量的梯度搜索,最佳带宽搜索历史部分中显示的最终 AICc 值通常与模型诊断部分中显示的 AICc 值略有不同。 发生这种情况是因为梯度搜索在带宽优化期间使用相邻要素数量的连续表示,这会导致每次迭代计算的 AICc 值出现少量不精确。 报告最终模型的 AICc 时,使用模型诊断部分中显示的值。
带宽汇总统计数据
带宽统计摘要部分总结了用于测试每个解释变量在每个局部模型中是否具有统计显著性的值。 这些统计数据包括 MGWR 的最佳邻域(相邻要素数或距离范围)、参数的有效数量、调整后的显著性水平 (alpha) 和调整后的伪 t 统计量临界值。 这些值用于为输出要素中的每个解释变量创建与统计显著性相关的字段。 调整后的 alpha 值通过显著性水平 (0.05) 除以参数的有效数量来计算;这控制了解释变量显著性的族错误率 (FWER)。 调整后的 alpha 用作具有有效自由度数的双边 t 检验中的显著性水平。
输出要素
该工具输出一个要素类,其中包括每个要素的本地诊断。 这些诊断包括回归残差、标准化残差、因变量的预测值、截距、解释变量系数、系数标准误差、系数伪 t 统计量、系数显着性、影响、Cook 距离、局部 R2 和条件数。 有关这些诊断的更多详细信息,请参阅地理加权回归的工作原理。
图表
以下图表已添加到内容窗格中:
- 变量之间的关系 - 具有 1 个因变量和最多 9 个解释变量的散点图矩阵,显示因变量与每个解释变量之间的相关性以及每对解释变量之间的相关性。 任何对之间的强相关性表明存在多重共线性。
- 标准化残差分布 - 标准化残差的直方图。 标准化残差应服从均值为零、标准差为 1 的正态分布。
- 标准化残差 VS 预测值 - 标准化残差与其相应预测值之间的散点图。 该图应该是随机的,并且不显示任何模式或趋势。
可选输出
可以在预测选项和附加选项下拉菜单中指定以下可选输出。
- 输出预测要素参数值是一个要素类,在预测位置参数指定的位置具有因变量的预测值。
- 输出邻域表参数值保存一个表,其中包含消息的系数估计值汇总统计和解释变量和邻域汇总部分的值。
- 系数栅格工作空间参数指定保存系数栅格的工作空间(目录或地理数据库)。 这些系数栅格表面可以帮助解释系数的空间变化。
多重共线性
当两个或多个解释变量在回归模型中高度相关时,就会出现多重共线性。 这可能发生在 OLS、GLR、GWR 和 MGWR 模型中。 多重共线性可能会对系数和最优邻域的估计产生负面影响,因为如果这些解释变量是相关的,则它们会相互共享信息,且回归模型无法区分变量的影响。 在中等情况下,估计的系数估计值可能存在偏差并且具有很高的不确定性。 在极端情况下,模型可能无法计算。 以下示例显示了三个相互高度相关的变量的散点图矩阵,使用它们作为解释变量的回归模型可能会遇到多重共线性问题。
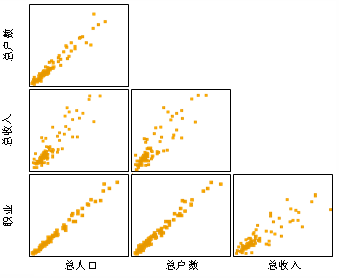
MGWR 中多重共线性的识别和预防
在 MGWR 模型中,多重共线性可能出现在多种情况下:
解释变量之一为强烈空间聚类。 由于 MGWR 适合局部回归模型,当一个要素及其所有邻域的解释变量值大致相同时,可能会出现多重共线性。
为防止这种情况,请映射每个解释变量并确定可能值很少或相同变量在空间上聚集的变量。 如果您观测到这些类型的变量,请考虑将它们从模型中删除或以增加值范围的方式表示它们。 例如,将可变数量的卧室更好地表示为每平方英尺的卧室。
两个或多个解释变量在全局范围内高度相关。
使用广义线性回归运行全局模型并检查每个解释变量的方差膨胀因子 (VIF)。 如果 VIF 值很大,例如 7.5 或更高,则全局多重共线性可能会阻止 MGWR 运行。 在这种情况下,变量是多余的,因此请考虑从模型中删除变量之一或将它们与其他解释变量组合以增加值的变化。
定义的邻域太小。
多重共线性也可以同时涉及多个解释变量,当某些解释变量的线性组合与其他解释变量的线性组合高度相关时,就会出现这种情况。 这在相邻要素数量较少的邻域中最为常见。 要对此进行测试,请检查输出要素类中的局部条件编号。 较高的局部条件数表明由于局部多重共线性,结果不稳定。 如果是这种情况,请使用更多的相邻要素或距离范围重新运行模型。 作为规则,对要素的条件数大于 30 或为空的结果持怀疑态度。 对于 shapefile,空值用值 -1.7976931348623158e+308 表示。 条件数经过比例调整以校正模型中解释变量的数量,这使您可以直接比较使用不同数量的解释变量的模型之间的条件数。
检查所有这些条件可能有助于解决多重共线性问题,但也许并不总能解决这些问题。
系数和带宽估计
对于除梯度搜索之外的所有邻域选择方法,通过被称为反向拟合的流程(Breiman 等人,1985 年)来估计解释变量的系数和带宽。 该程序最初是为估计广义加性模型的参数而开发的,可逐个遍历解释变量,并使用平滑函数来校准系数,同时保持所有其他解释变量不变。 此流程将在解释变量上重复,直到系数的值稳定并且在连续迭代后不改变。
当应用于 MGWR (Fotheringham et al. 2017) 时,平滑函数是一个单变量 GWR 模型,将先前的残差调整预测与单个解释变量(将所有其他解释变量视为常数)进行回归。 此 GWR 模型使用相同的邻域选择方法(黄金搜索、手动间隔或用户自定义)来估计解释变量的空间比例。 有关该流程的完整描述,请参阅附加资源部分。
反向拟合算法必须从系数的初始化值开始。 这些初始值由所有解释变量的 GWR 模型估计。 如果此模型由于多重共线性而失败,则改用 OLS。 如果该流程在 25 次迭代后仍未收敛,则使用最后一次迭代的系数值。
梯度搜索
梯度搜索邻域选项方法选项是一种更新的方法,用于估计 MGWR 中的最佳带宽,不使用反向拟合。 梯度搜索的主要好处是改进运行时间和有效使用内存。 该方法是一种二阶优化算法,它使用梯度和 Hessian 矩阵来最小化关于解释变量空间尺度的 AICc。 不是在每个迭代步骤中更新单个解释变量的参数,而是通过沿梯度的最陡方向下降同时更新所有解释变量的参数,并通过 AICc 的曲率进行校正。
黄金搜索和梯度搜索产生的结果通常非常相似。 下图显示了真实的系数表面以及使用黄金搜索和梯度搜索估计的系数表面。 请注意,所有表面都是相似的,并准确估计真实表面。
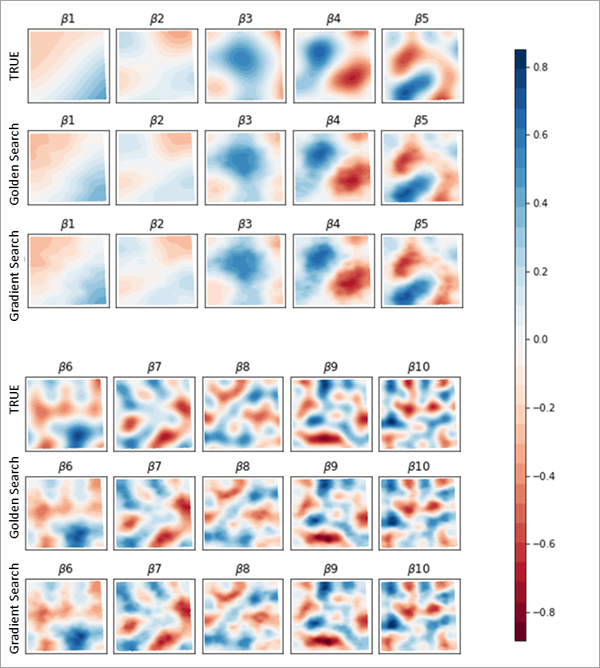
下图比较了在不同数量的解释变量和不同数据集大小的情况下,黄金搜索和梯度搜索的运行时间。 请注意,对于相同数量的解释变量,梯度搜索的运行时间始终约为黄金搜索运行时间的一半。
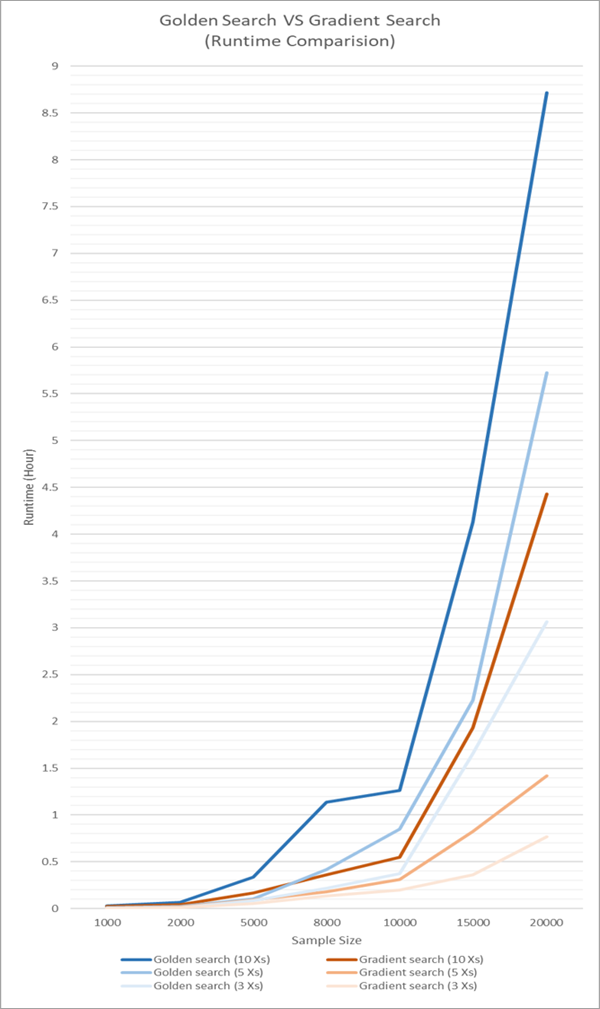
下图比较了梯度搜索和黄金搜索的内存使用情况。 黄金搜索的内存使用量随着样本量的增加而迅速增加(二次增长),而梯度搜索的内存使用量不受样本量的影响。
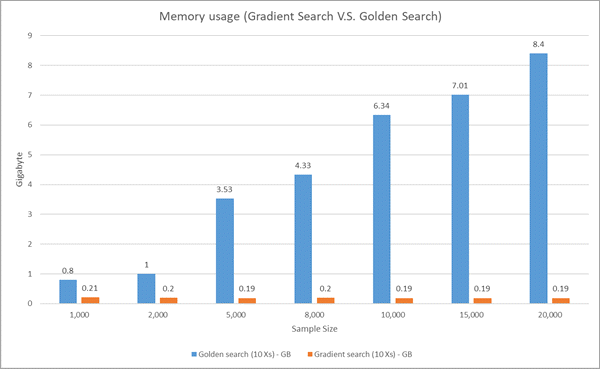
下图比较了梯度搜索和黄金搜索的 AICc 值。 这两种方法的准确性非常相似,但黄金搜索获得的 AICc 值略低于梯度搜索(表明估计略微更准确)。
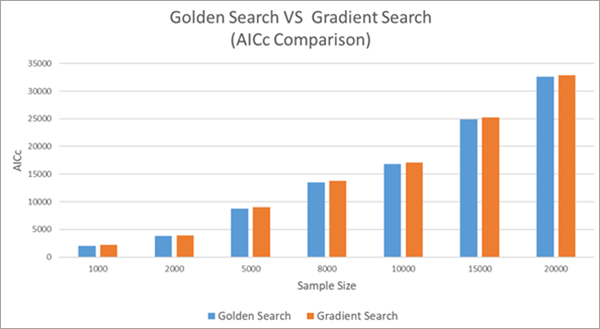
其他资源
有关详细信息,请参阅以下资源:
- Breiman, L., and J. H. Friedman. 1985. "Estimating optimal transformations for multiple regression and correlations (with discussion)." Journal of the American Statistical Association 80, (391): 580–619. https://doi.org/10.2307/2288473. JSTOR 2288473.
- Brunsdon C., A. S. Fotheringham, and M. E. Charlton. 1996. "Geographically weighted regression: A method for exploring spatial nonstationarity." Geographical Analysis 28: 281–298.
- Conn, A.R., N.I.M. Gould, and P.L. Toint. 2000. "Trust Region Methods." Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9780898719857.
- da Silva, A. R., and A. S. Fotheringham. 2016. "The multiple testing issue in geographically weighted regression." Geographical Analysis 48(3), 233–247. https://doi.org/10.1111/gean.12084.
- Fotheringham, A. S., W. Yang, and W. Kang. 2017. "Multiscale geographically weighted regression (MGWR)." Annals of the American Association of Geographers 107: 1247–265. https://doi.org/10.1080/24694452.2017.1352480
- Oshan, T. M., Z. Li, W. Kang, L. J. Wolf, and A. S. Fotheringham. 2019. "mgwr: A Python implementation of multiscale geographically weighted regression for investigating process spatial heterogeneity and scale." ISPRS International Journal of Geo-Information 8: 269.
- Yu, H., A. S. Fotheringham, Z. Li, T. Oshan, W. Kang, and L. J. Wolf. 2020. "Inference in multiscale geographically weighted regression." Geographical Analysis 52: 87–106.
- Zhou, X., R. Assunção, H. Shao, M. Janikas, C. Huang, and H. Asefaw. 2023. "Gradient-based optimization for Multi-scale Geographically Weighted Regression." (under review)