


Анализ связей базируется на анализе взаимоотношений, соединений и связей внутри набора данных. Анализ связей дает вам возможность рассчитать некоторые измерения центральности, а именно, степень, промежуточность, близость и собственный вектор, и увидеть связи на диаграмме связей или на карте связей.
Об анализе связей
Анализ связей использует связи по сети или внутренние связи и узлы для идентификации и анализа отношений, которые, при первом взгляде на данные, могут быть не очевидны. Основные типы сетей:
- Социальные сети – кто с кем общается
- Семантические сети – например, разделы текста, связанные друг с другом по смыслу
- Конфликтные сети – указывают связи между игроками
- Сети авиасообщений с указанием аэропортов, имеющих стыковочные рейсы
Примеры
Криминалист занимается исследованием преступной сети. Данные из записей сотовых телефонов можно использовать для определения отношений и иерархии между участниками сети.
Фирма по обслуживанию кредитных карт разрабатывает новую систему для обнаружения краж по кредитным картам. Система использует известные схемы транзакций для каждого клиента, такие как городские траты, покупки в магазинах и типы транзакций, чтобы выявить отклонения от привычной схемы и предупредить клиента о возможной краже.
Аналитик в системе здравоохранения изучает всплеск употребления наркотиков в Северной Америке. Он использует данные о выдаче рецептов на опиоидные средства и данные демографии для идентификации новых закономерностей, свидетельствующих о возможном росте пациентов с наркотической зависимостью.
Как работает инструмент Анализ связей
В следующей таблице представлен обзор терминов в анализе связей:
| Термин | Описание | Примеры |
|---|---|---|
Сеть | Набор связей, соединенных между собой. | Социальная сеть в интернете, которая функционирует на основе отношений между пользователями в этой сети. Сети авиасообщений, которые используют взаимосвязь аэропортов и рейсов для перевозки путешественников от исходной точки до точки назначения. |
Узел | Точка или вершина, представляющая объект, например, человека, место, тип преступления или запись в соц. сети. Узел может также включать связанные с ним свойства. | Профиль в социальной сети. Связанные свойства могут включать имя пользователя, родной город, должность. Аэропорты в сети авиасообщений. Связанные свойства могут включать название аэропорта. |
Связь | Отношения или соединения между узлами. Связь может также включать связанные с ней свойства. | Отношения между профилями в социальной сети, например, друзья, в одной группе, подписка на обновления. Связанные свойства могут включать длину связи. Авиарейсы между аэропортами в сети авиасообщений. Связанные свойства могут включать число рейсов между двумя аэропортами. |
Центральность
Центральность – мера важности для узлов в сети.
Определение центральности используется для следующих целей:
- Для оценки важности узла по отношению к остальным узлам в сети. Например, опубликованная каким из пользователей новость или вакансия, быстрее всего распространится среди других пользователей
- Для выявления наиболее важного узла по отношению к другим узлам. Например, какой аэропорт больше всего пострадает при отмене рейсов из-за непогоды в другом регионе?
- Для изучения потока или распространения чего-либо по сети, включая информацию, объект или феномен. Например, каким образом посылка транспортируется со склада на адрес доставки?
- Для понимания, через какие узлы распространение феномена произойдет более эффективно. Например, в каком СМИ опубликовать новость, чтобы она была прочитана максимальным числом людей?
- Для определения узлов, которые могут останавливать или тормозить распространение феномена. Например, где стоит расположить центры вакцинации, чтобы максимально быстро остановить распространение вируса?
Есть четыре способа измерения центральности в Insights: степень центральности, промежуточность центральности, близость центральности и центральность собственного вектора.
Вычисления центральностей промежуточности, близости и собственного вектора могут быть взвешенными и невзвешенными.
Степень центральности
Степень центральности рассчитывается по числу прямых подключения к узлу. Степень центральности используется для определения узлов, которые имеют наибольшее прямое влияние. Например, в социальной сети пользователи с большим числом подписчиков имеют большую степень центральности.
Степень центральности узла x вычисляется с использованием следующего равенства:
degCentrality(x)=deg(x)/(NodesTotal-1), где:
- Узлы Всего = число узлов в сети
- deg(x) = число узлов, подключенных к узлу x
Если связи имеют направление, то есть информация между узлами может проходить только в одном направлении, степень центральности можно рассчитать как входящую, так и исходящую. В примере с социальной сетью, входящую степень можно вычислить, как число профилей, на которые подписан пользователь, а исходящую – число подписчиков этого пользователя.
Входящая степень центральности вычисляется с использованием следующего равенства:
indegCentrality(x)=indeg(x)/(NodesTotal-1), где:
- Узлы Всего = число узлов в сети
- Indeg(x) = число узлов, подключенных к узлу x, поток от которых идет в направлении к узлу x
Исходящая степень центральности вычисляется с использованием следующего равенства:
outdegCentrality(x)=outdeg(x)/(NodesTotal-1), где:
- Узлы Всего = число узлов в сети
- outdeg(x) = число узлов, подключенных к узлу x, поток от которых идет в направлении от узла x
Для графиков с направлением, Insights по умолчанию определяет размеры узлов по исходящей степени центральности.
Промежуточность центральности
Промежуточность центральности рассчитывается по экстенту, в котором узел является частью кратчайшего пути между другими узлами. Промежуточность центральности используется, если вы хотите определить, какие узлы используются для связи с других узлов друг с другом в сети. Например, пользователь в социальной сети, участвующий в нескольких группах друзей, будет иметь промежуточность центральности выше, чем пользователь, участвующий только в одной группе.
Промежуточность центральности для узла x вычисляется с использованием следующего равенства:
btwCentrality(x)=Σa,bϵNodes(pathsa,b(x)/pathsa,b), где:
- Узлы = все узлы в сети
- пути a,b = число кратчайших путей между всеми узлами a и b
- пути a,b(x) = число кратчайших путей между узлами a и b которые связаны через узел x
Приведенное выше уравнение промежуточности центральности не учитывает размер сети, поэтому большие сети, как правило, имеют большие значения промежуточности центральности, чем сети небольшого размера. Чтобы обеспечить возможность сравнения между сетями различных размеров, уравнение промежуточности центральности должно быть нормировано путем деления на число пар узлов на диаграмме.
Для нормирования диаграммы без направлений используется следующее равенство:
1/2(NodesTotal-1)(NodesTotal-2), где:
- Узлы Всего = число узлов в сети
Для нормирования диаграммы с направлениями используется следующее равенство:
(NodesTotal-1)(NodesTotal-2), где:
- Узлы Всего = число узлов в сети
Близость центральности
Близость центральности рассчитывается по среднему расстоянию между узлами по кратчайшему пути в сети. Близость центральности используется, если вы хотите определить, какие узлы расположены наиболее близко к другим узлам в сети. Например, пользователь в социальной сети с большим числом друзей характеризуется более высоким значением близости к центру, чем пользователь, который связан с другими не напрямую (друзья друзей).
Примечание:
Расстояние между узлами относится к числу связей между ними, а не к географическому расстоянию.
Близости к центру для узла x вычисляется с использованием следующего равенства:
closeCentrality(x)=(nodes(x,y)/(NodesTotal-1))*(nodes(x,y)/dist(x,y)Total), где:
- Узлы Всего = число узлов в сети
- nodes(x,y) = число узлов, подключенных к узлу x
- dist(x,y)Всего = сумма расстояний по кратчайшему пути от узла x к другим узлам
Центральность собственного вектора
Центральность собственного вектора базируется на важных узлах, которые соединяются с другими важными узлами. Центральность собственного вектора используется для определения того, какие узлы являются частью кластера влияния. Например, пользователей в социальной сети с большим числом соединений с другими пользователями с также большим числом соединений будет иметь большую центральность собственного вектора, чем пользователь с меньшим числом подключений или чем пользователь, который соединен с другими пользователями, у которых мало подключений.
Центральность собственного вектора узла x вычисляется с помощью степенной итерации для поиска наибольшего собственного вектора на основе следующего выражения:
Ax=λx, где:
- λ = собственное число
- x = собственный вектор
- A = матрица, описывающая линейную трансформацию
Вес ребра
Вычисления центральностей промежуточности, близости и собственного вектора могут быть взвешенными и не взвешенными. При невзвешенном вычислении центральности ребрам присваивается единый вес, равный 1, тогда как взвешенное вычисление использует значения в полях для присвоения значения каждому ребру.
Примечание:
Незаданным весам присваивается значение, равное 1. Рекомендуется для веса ребра назначать поле без нулевых и пустых значений.
Для центральности собственного вектора веса используются с целью определения силы связи между узлами. Поскольку центральность собственного вектора измеряет важность узлов сети, более высокие значения веса соответствуют более высоким значениям их соединяющих узлов.
Для центральностей близости и промежуточности значения весов соответствуют расстоянию между узлами. Более высокие веса ребер означают большее расстояние между узлами и снижают вероятность использования ребра в кратчайшем пути. Если более высокое число в поле желаемого веса указывает на увеличившуюся важность (например, количество сообщений, отправленных участниками в социальной сети, указывает на то, насколько связаны участники), новое поле должно быть вычислено с обратными значениями. Для вычисления обратных значений в поле воспользуйтесь следующим уравнением:
вес=ABS(поле-MAX(поле))+IF(MIN(поле)<0, ABS(MIN(поле)), MIN(поле))При расчета невзвешенной близости или промежуточности кратчайшим путем будет путь, использующий наименьшее число ссылок. В расположенном ниже примере показаны сеть с четырьмя узлами (A, B, C и D) с равными весами. Есть два пути с общим узлом от A до D: A-B-D и A-B-C-D. Поскольку у A-B-D меньше связей, этот путь является кратчайшим.

Взвешенное вычисление применяет веса к каждому ребру на основе значений в поле. Взвешенные центральности близости и промежуточности используют для поиска кратчайших путей между узлами алгоритм Беллмана-Форда .
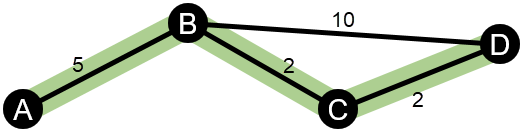
В расположенном ниже примере показаны сеть с четырьмя узлами и взвешенными ребрами. У пути A-B-D значение равно 15, а у пути A-B-C-D - 9. Поскольку у A-B-C-D ниже значение суммы ребер, это кратчайший путь.
Взвешенные вычисления центральностей промежуточности и близости не поддерживают отрицательные циклы веса. При обнаружении отрицательного цикла веса всем значениям центральностей присваивается 0. Отрицательный цикл веса может появиться в следующих случаях:
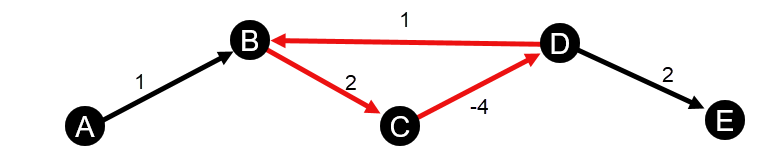
- Диаграмма содержит отрицательный цикл веса.
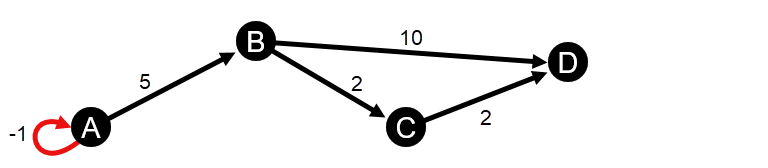
- Диаграмма содержит отрицательное самопересечение.
- Диаграмма не является направленной и содержит отрицательное ребро.
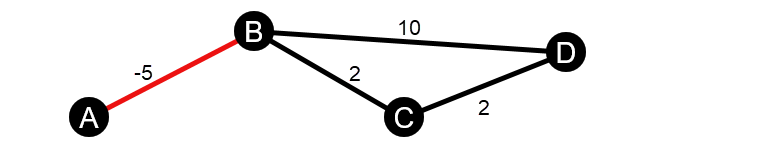
Что дальше
Выполните эти основанные на реальных сценариях упражнения Learn ArcGIS для изучения управляемых рабочих процессов с анализом связей: