Инструмент Мультимасштабная географически взвешенная регрессия (МГВР) применяет продвинутую методику пространственной регрессии, которая используется в географии, городском планировании и различных других отраслях. В этом инструменте улучшен алгоритм моделей Географически взвешенной регрессии (ГВР), где используются зависимая и независимые переменные в пределах окрестности целевого объекта для построения локальной линейной регрессии для интерполяции или прогнозирования.
Основная идея ГВР в том, что использование единой регрессионной модели для большой географической области может быть налагать слишком сильные ограничения. Географически взвешенная регрессия позволяет использовать разные регрессионные модели в каждом пространственном местоположении, и коэффициенты регрессии постепенно меняются по всей территории региона. То есть в разных местоположениях области изучения независимые переменные по-разному влияют на зависимую переменную. ГВР достигает этого путем создания взвешенной модели регрессии для каждого пространственного объекта, используя зависимую и независимые переменные самого объекта и его пространственных соседей. Соседние объекты, расположенные ближе к этому объекту, получают больший вес и большее влияние на локальную модель регрессии.
МГВР является расширением ГВР, и позволяет в окрестности вокруг каждого объекта по-разному использовать разные независимые переменные. То есть, для некоторых независимых переменных окрестность может быть больше или меньше чем для других независимых переменных. Возможность использовать разные окрестности для разных независимых переменных очень важна, так как отношения между независимыми и зависимой переменной могут возникать в различных пространственных масштабах: коэффициенты для некоторых переменных могут постепенно меняться в области изучения, а для других переменных - наоборот, меняться резко. Сопоставление окрестности для каждой независимой переменной с пространственным масштабом этой независимой переменной позволяет МГВР более точно вычислять коэффициенты в локальной модели регрессии.
МГВР применима для больших наборов данных, где есть, как минимум, несколько сотен объектов, и наборов данных, в которых зависимая переменная демонстрирует пространственную неоднородность. Для моделирования пространственных отношений в наборах данных меньшего размера лучше использовать другие инструменты. Сейчас инструмент Мультимасштабная географически взвешенная регрессия (МГВР) допускает использование только зависимых переменных с непрерывным типом данных. Не запускайте инструмента с данными количеств или с бинарными данными. Это может привести к смещению модели и бессмысленным результатам.
В основном в данной статье сравнивается МГВР с другими моделями регрессии. Рекомендуем изучить основы регрессии по Методу наименьших квадратов (МНК) и познакомиться с понятиями окрестностей, схемы весов и проверок ГВР перед тем, как продолжать.
Более подробно о регрессии МНК
Выбор модели регрессии
МНК, ГВР и МГВР - линейные модели регрессии, но они оперируют разными пространственными масштабами и используют разные допущения о пространственной неоднородности (стационарности отношений в пределах области изучения) в наборе данных. МНК - глобальная модель регрессии. Она предполагает, что процессы генерации данных постоянны в пространстве, поэтому единый коэффициент может учитывать отношения между зависимой и каждой независимой переменной везде. ГВР - это локальная модель, в которой более мягкие представления о пространственной стационарности, соответственно коэффициенты могут меняться в пространстве. Тем не менее, ГВР предполагает, что все локальные отношения находятся в едином пространственном масштабе, то есть для всех независимых переменных используется одна и та же окрестность. Например, если одна независимая переменная использует 20 соседей для вычислений, все остальные независимые переменные тоже должны использовать 20 соседей.
А МГВР не только допускает варьирование коэффициентов в пространстве анализа, но так же и различный масштаб окрестности для разных независимых переменных. Это выполняется путем использования окрестностей разного размера для каждой независимой переменной, что позволяет учесть разный масштаб пространственных отношений между каждой независимой и зависимой переменной. В свою очередь, это дает возможность комбинировать независимые переменные, оперирующие в относительно больших пространственных масштабах, такие как температура и атмосферное давление с переменными небольших масштабов, например, численность населения или средний доход.
МГВР более точно оценивает локальные коэффициенты и выдает меньше ошибок, связанных с мультиколлинеарностью, чем ГВР. Но время обработки для МГВР существенно выше, чем ГВР, особенно если установлены опции Золотой поиск, Интервалы вручную или Определен пользователем в параметре Метод выбора окрестности. Есть три метода выбора окрестности, основанные на алгоритме обратной подгонки, что требует больших вычислений и использования большого объема памяти. По мере увеличения размера данных увеличивается время выполнения и объем задействованной памяти.
При выборе типа модели, применимой для ваших данных, ответьте на следующие вопросы:
- Должна ли моя модель запускаться на локальном или глобальном уровне.
- Если вас интересует локальная модель, используйте ГВР или МГВР. Если же нет, используйте МНК или другую модель, например Классификация на основе леса и регрессия.
- Будут ли независимые переменные в моей модели оперировать разными пространственными масштабами?
- Если вы предполагаете, что независимые переменные могут оперировать разными пространственными масштабами, и вы хотите учесть в модели эти разные масштабы, примените МГВР.
- Насколько велик мой набор данных? Насколько долго я готова ждать результатов?
- Если у вас большой набор данных и вы запускаете инструмент МГВР, вы должны быть готовы к продолжительному времени работы инструмента. При использовании обычного оборудования начала 2020-х годов (16 логических процессоров и 32 Гб памяти) и стандартных параметров для наборов данных размером более 10000 точек, время выполнения скорее всего составит несколько часов. Для 50000 точек время выполнения может занять несколько дней. Для 100000, скорее всего, будет ошибка использования памяти.
Если вы все еще не уверены, какую локальную модель использовать для ваших данных, ГВР или МГВР, начните с МГВР. Запуск МГВР также подразумевает и ГВР, при определенных настройках. В сообщениях геообработки вы можете найти проверки ГВР и сравнить их с проверками МГВР. Или же вы можете запустить несколько инструментов (МНК, ГВР и МГВР) и использовать значения критерия AIC в сообщениях геообработки для сравнения моделей и выбора лучшей. Если вы запускаете несколько инструментов, масштабируйте все модели или оставьте все модели немасштабированными, чтобы результаты были сопоставимы.
Возможное применение
МГВР можно применять для множества различных анализов и ответов на вопросы, в частности, такие:
- Как различные характеристики, такие как количество комнат, год постройки, площадь участка и так далее, влияют на цену дома? Существенно ли различаются отношения в разных сообществах?
- Как распределение PM2.5 связанно с экономическими переменными, такими как доходы домохозяйств в регионе, число машин на домохозяйство или процент валового внутреннего продукта, приходящегося на сельское хозяйство?
- В точном земледелии влияют ли типы почв на урожайность сельскохозяйственных культур в том же пространственном масштабе, что и метеорологические переменные, такие как температура, влажность и осадки?
Производительность и контрольные показатели
Множество факторов влияют на время выполнения МГВР. Основной фактор для времени выполнения - число объектов. С ростом числа объектов время выполнения возрастает в кубе. Размер окрестности и число независимых переменных также влияет на время выполнения МГВР, так как требует больше вычислений для каждой локальной модели. Для выполнения вычислений максимально быстро, МГВР задействует параллельную обработку на компьютере. Для некоторых вычислений используются все доступные ядра, а для остальных вычисления определяются параметром среды Коэффициент параллельной обработки.
Входные данные инструмента
Есть разные методы указания пространственного масштаба для независимых переменных.
Выбор окрестности (ширина полосы)
Ключевое преимущество метода МГВР - возможность использовать разные окрестности (ширину полосы) для каждой независимой переменной в уравнении линейной регрессии. Окрестность для независимой переменной в целевом местоположении включает все местоположения, которые участвуют в оценке коэффициента незакисимой переменной в локальной модели регрессии. Каждая окрестность задается числом соседей вокруг целевого объекта, или всеми соседями в пределах фиксированного расстояния. Число соседей или расстояние может быть разным для каждой независимой переменной.
Существует четыре опции для параметра Метод выбора окрестности, которые можно использовать для расчета оптимального пространственного масштаба для каждой независимой переменной:
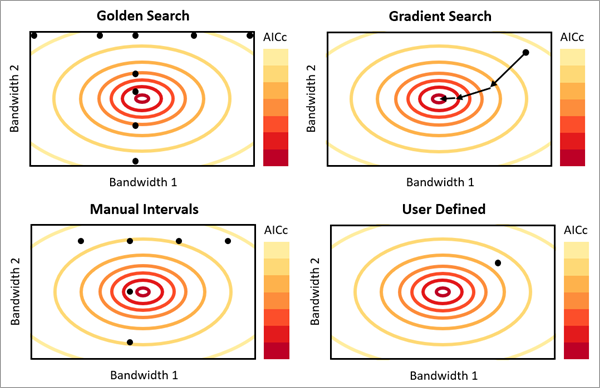
Золотой поиск — определяет расстояние или число соседних объектов для каждой независимой переменной, с использованием алгоритма Золотого поиска. В рамках этого метода ищутся различные комбинации переменных для каждой независимой переменной между указанными минимальными и максимальными значениями. Это итеративный процесс, использующий результаты предыдущих комбинаций для выбора новой комбинации для тестирования. Итоговые значения выбираются по наименьшему AIC. Если выбрана опция Число соседей, минимальные и максимальные значения указываются в параметрах Минимальное число соседей и Минимальное число соседей. Для опции диапазона расстояний минимальные и максимальные значения указываются в параметрах Минимальное расстояние поиска и Максимальное расстояние поиска. Минимальные и максимальные значения распространяются на все независимые переменные, но рассчитанное число соседей или диапазон расстояний будут разными для каждой независимой переменной (кроме двух или более совпадающих, с одинаковым пространственным масштабом). Эта опция требует больше времени для вычисления, особенно для больших наборов данных и наборов данных с большим диапазоном значений.
Градиентный поиск — определяет расстояние или число соседних объектов для каждой независимой переменной, с использованием алгоритма оптимизации на основе градиента. Чтобы подобрать оптимальную ширину полосы для каждой независимой переменной, Градиентный поиск берет значения AIC, связанные с каждым значением ширины полосы, и обновляет эти значения, пока не подберет наименьший AIC. Если выбрана опция Число соседей, минимальные и максимальные значения указываются в параметрах Минимальное число соседей и Минимальное число соседей. Для опции Диапазона расстояний минимальные и максимальные значения указываются в параметрах Минимальное расстояние поиска и Максимальное расстояние поиска. Так же, как и для Золотого поиска, Минимальные и максимальные значения распространяются на все независимые переменные, но рассчитанное число соседей или диапазон расстояний будут разными для каждой независимой переменной (кроме двух или более совпадающих, с одинаковым пространственным масштабом). Эта опция формирует окрестности, сопоставлимые с опцией Золотой поиск, но выполняется значительно быстрее, и с меньшим расходом памяти.
Интервалы вручную — определяет расстояние или число соседних объектов для каждой независимой переменной, ступенчато увеличивая число соседей или расстояние, начиная с минимального значения. Для опции числа соседей метод начинает со значения параметра Минимальное число соседей. Число соседей затем увеличивается на значение, указанное в параметре Инкремент числа соседей. Этот инкремент повторяется определенное количество раз, в соответствии с установкой в параметре Число инкрементов. Для опции Диапазона расстояний метод использует параметры Минимальное расстояние, Инкремент расстояния поиска и Число инкрементов. Число соседей или диапазон расстояния, используемый для каждой независимой переменной будет представлен одним из протестированных значений, но значения могут быть разными для разных независимых переменных. Эта опция выполняется быстрее, чем Золотой поиск, и часто рассчитывает сопоставимые окрестности.
Определен пользователем — число соседей или расстояние поиска, используемое независимыми переменными. Это значение указывается в параметре Число соседей или Диапазон расстояний. Эта опция обеспечивает вас большим контролем, если вы знаете оптимальные значения.
По умолчанию все параметры окрестности, относящиеся к выбранному методу окрестности, применяются ко всем независимым переменным. Но настраиваемые параметры выбора окрестности можно применить только к определенным независимым переменным, используя соответствующие замещающие параметры для типа окрестности и метода выбора: Число соседей для Золотого поиска, Число соседей для Градиентного поиска, Число соседей для интервалов вручную, Заданное пользователем число соседей, Расстояние поиска для Золотого поиска, Расстояние поиска для Градиентного поиска, Расстояние поиска для интервалов вручную или Заданное пользователем расстояние поиска. Чтобы использовать настраиваемую окрестность для конкретных независимых переменных, укажите независимые переменные в первом столбце соответствующего замещающего параметра, и укажите настраиваемые опции для окрестности в других столбцах. Столбцы названы теми же именами, что и замещающие параметры; например, если вы используете интервалы вручную для диапазона расстояний, столбец Инкремент расстояния поиска будет содержать настроенные значения для параметра Инкремент расстояния поиска. В панели Геообработка настроенные параметры окрестности отображаются в категории параметров Настраиваемые опции окрестности.
Например, допустим, вы используете три независимых переменных с типом окрестности Золотой поиск и 30 минимальным и 40 максимальным числом соседей. Если инструмент запустится с этими параметрами, каждая из трех независимых переменных будет использовать в расчетах данные от 30 до 40 соседних объектов. Если же вы хотите использовать от 45 до 55 соседей только для второй независимой переменной, вы можете указать вторую независимую переменную, пользовательское значение минимума и пользовательское значение максимума в столбцах параметра Число соседей для золотого поиска. Таким образом, для первой и третьей независимых переменных будут использоваться данные от 30 до 40 соседей, а вторая независимая переменна будет использовать в расчетах данные от 45 до 55 соседних объектов.
Схема присвоения локальных весов
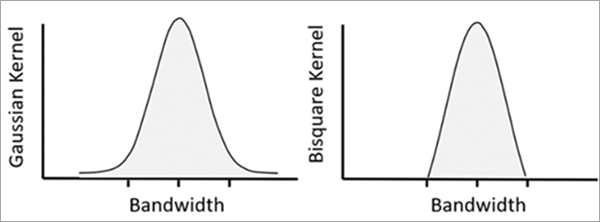
МГВР оценивает локальную модель регрессии для каждого целевого объекта путем применения географически-взвешенной функции (функции ядра) к объекту и его окрестности. Соседние объекты, расположенные ближе к целевому объекту имеют большее влияние на результаты локальной модели. Две опции ядра доступны в параметре Схеме присвоения локальных весов, - Гауссова и Биквадрат. Более подробно о работе географических весах с ядрами см. в разделе как работает Географически взвешенная регрессия. В МГВР взвешенная ширина полосы варьирует для разных независимых переменных.
Примечание:
Градиентный тип поиска окрестности доступен только для опции биквадратного ядра. Опция Гауссова ядра может быть доступна в последующих версиях.
Выбор данных и коэффициентов
По умолчанию все значения независимых и зависимой переменной масштабированы, так, чтобы среднее значение было равно нулю, а среднеквадратическое отклонение равно 1 (также называется Стандартизация z-оценки). Оценки коэффициентов масштабированных значений данных интерпретируются в среднеквадратических отклонениях; например, коэффициент 1.2 означает, что увеличение на одно среднеквадратическое отклонение в независимой переменной соответствует увеличению на 1.2 среднеквадратических отклонения в зависимой переменной. Так как все коэффициент используют общие единицы измерения, значения можно сравнивать напрямую, и видеть, какая из независимых переменных обладает большим влиянием на модель. Общая рекомендация - масштабировать переменные, но в особенности важно масштабирование, если диапазон значений в переменных существенно варьируется. Вы можете выбрать - не масштабировать данные, сняв отметку с параметра Масштабировать данные.
В большинстве линейных моделей регрессии, таких как МНК или ГВР, коэффициенты не меняются в линейном масштабировании. Это означает. что если вы масштабируете исходные данные, подгоняете модель, затем обратно пересчитываете результат в исходные единицы - результаты будут такими же, как если бы вы не масштабировали данные. В МГВР масштабирование и обратный пересчет не приведут к построению той же модели, что и на исходных данных. Это потому, что обратная подгонка - итеративный процесс, где результат каждого шага зависит от результатов предыдущих шагов. Использование различных начальных масштабов влияет на траекторию тестируемых значений и приводит к созданию разных моделей МГВР. Масштабированные результаты обычно более точные, так как масштабирование выравнивает дисперсию переменных и итерации процесса сходятся быстрее и ведут к более точным значениям, если каждая переменная вносит равный вклад в общую дисперсию данных. Если независимые переменные имеют разную дисперсию (например, из-за разных единиц измерения), переменные с большей дисперсией сильнее влияют на каждый шаг итеративной оценки. В большинстве случаев это отрицательно влияет на результирующую ширину полосы и коэффициенты модели.
Для более простой интерпретации масштабированных результатов, все коэффициенты в выходных данных инструмента приведены в масштабированном значении, и не в масштабированном (исходном) измерении данных. Выходные данные содержат дополнительные поля выходных объектов (также добавленные как слои в выходном составном слое) и дополнительные растры в директории Выходная рабочая область растровых коэффициентов. При прогнозировании новых местоположений с использованием параметров Прогнозируемые местоположения и Выходные прогнозированные объекты, все прогнозируемые значения не масштабированы. См. Выходные данные инструмента для дополнительной информации о выходных данных.
Выходные данные инструмента
Инструмент создает разные выходные данные, включая составные слои, с различными полями с сообщениями выходных объектов, а также диаграммы. Дополнительные выходные данные включают класс объектов прогнозируемых значений в новых местоположениях, таблицу окрестностей и растровые поверхности для каждого коэффициента.
Составные слои и символы
Выходные символы слоя по умолчанию визуализируют нормированные невязки локальной линейной модели регрессии с использованием цветовой схемы классификации. Изучение закономерностей в невязках позволяет понять, насколько модель хорошо настроена. Распределение невязок в корректной модели регрессии будут соответствовать нормальному распределению и оно должно быть пространственно случайным (не образовывать кластеры). Можно запустить инструмент Пространственная автокорреляция (Индекс Морана I) для невязок регрессии, чтобы убедиться, что они пространственно случайны. Статистически значимая кластеризация высоких и/или низких значений невязок указывает на то, что модель МГВР не оптимальна.
Слои коэффициентов и статистической значимости каждой независимой переменной добавляются в составной слой карты, в виде отдельных подслоев для каждой независимой переменной. Каждый слой коэффициентов представлен сходящейся цветовой схемой, центрированной на нулевом значении. Это позволяет вам использовать цвет для понимания того, какая переменная связана положительными или отрицательными отношениями с зависимой переменной. Для точек, статистически значимые объекты (95% значимости) обозначаются гало зеленого цвета вокруг точек, а незначимые отношения обозначены гало серого цвета. Для полигонов значимые отношения указываются с помощью сетчатых текстур. Изучите слои коэффициентов и слои значимости для лучшего понимания пространственной вариабельности в независимых переменных. Вы можете использовать свое понимание пространственной вариабельности для обоснования правил. Глобальные правила могут подойти, если переменные глобально статистически значимы и демонстрируют незначительные региональные различия, но локальные правила лучше подходят при наличии существенных пространственных различий в коэффициентах регрессии. В этом случае можно определить правила в тех областях, где наблюдается выраженный положительный эффект. Но те же правила могут не подойти в других областях, где эффект отрицательный и не сильно выражен.
Сообщения и проверки
Сообщения проводят информацию о модели МГВР и ее производительности. Сообщения имеют несколько разделов.
Суммарная статистика для оценок коэффициентов
В разделе Суммарная статистика для оценок коэффициентов приведены значения среднего, среднеквадратического отклонения, минимум, медиана и максимум оценок коэффициентов в изучаемой области. Среднее значение каждого коэффициента отражает связь между независимой и зависимой переменной. Среднеквадратическое отклонение указывает на пространственную вариабельность каждой независимой переменной. Невысокие значения среднеквадратического отклонения дают основание думать, что простейший метод, типа МНК, вполне адекватен для таких данных. Если отмечен параметр Масштабировать данные, вы можете сравнивать значения всех независимых переменных. Если параметр Масштабировать данные не отмечен, значения коэффициентов независимых переменных нельзя сравнить напрямую, так как единицы измерения могут отличаться.
Проверки модели
В разделе Проверки модели содержится таблица, показывающая несколько проверок модели для ГВР и МГВР, включая R2, Выровненный R2, AIC, дисперсию невязок и число эффективных степеней свободы. Для дополнительной информации о проверках модели см. Как работает инструмент Географически взвешенная регрессия.
Примечание:
В некоторых случаях построение модели ГВР для сравнения может не получиться. Тогда показаны только проверки МГВР
Вы можете использовать R2 и выровненный R2 для оценки степени соответствия модели данным. Чем выше R2 и скорректированный R2, тем лучше модель соответствует данным. Оценка сложности модели проводится по числу независимых переменных и проверке числа эффективных степеней свободы. Простые модели имеют большое значение эффективных степеней свободы и меньше параметров. Если в модели слишком много параметров, запуск ее может нести риск излишней подгонки данных. Проверка критериев AIC позволяет оценить и степень подгонки и сложность модели. Инструмента Мультимасштабная географически взвешенная регрессия выбирает модель с наименьшим значением AIC.
Сводка независимых переменных и окрестностей
В разделе Сводка независимых переменных и окрестностей отображаются оценки окрестностей и уровней значимости для каждой независимой переменной. Если окрестность определяется числом соседей, оптимальное число соседей отображается как число, а также в виде процента от общего числа входных объектов. Если окрестность определяется шириной полосы, оптимальное расстояние отображается вместе с процентом от диагонали экстента входных объектов. Процент от числа объектов или величины экстента удобно использовать для оценки пространственного масштаба независимых переменных; например, если независимая переменная использует 75 процентов всех объектов в качестве соседей, такая локальная модель регрессии ближе к глобальной, чем к локальной (что говорит о том, что допустимо использовать МНК). А если другая локальная переменная использует только 5 процентов входных объектов как соседей, эта модель значительно ближе к локальной. Для всех типов окрестностей, число и процент статистически значимых локальных моделей с уровнем достоверности в 95 процентов отображается для каждой независимой переменной.
История поиска оптимальной ширины полосы
В разделе История поиска оптимальной ширины полосы отображается история поиска оптимальных расстояний вместе со значениями AIC для каждого из тестируемых значений. Инструмент начинает поиск оптимальной ширины полосы для каждой независимой переменной с того, что назначает каждой переменной одно и то же значение - оптимальную ширину полосы для ГВР. Далее инструмент настраивает ширину полосы и коэффициент каждой переменной в каждой итерации и оценивает новое значение AIC. В процессе итераций значение AIC снижается до постоянного уровня, или точки, с которой идет повышение, что определяет конец итераций. Опция Определен пользователем обычно требует меньше итераций, а Золотой поиск - больше. Хотя Градиентный поиск использует большое число итераций, время обработки для этой опции невысоко, так как каждая итерация выполняется достаточно быстро.
Примечание:
Для Градиентного поиска с числом соседей, финальное значение AIC, которое отображается в разделе истории поиска оптимальной ширины полосы будет несколько отличаться от значения AIC в разделе информации по диагностике модели. Это происходит потому что Градиентный поиск использует непрерывное представление числа соседей в процессе подбора оптимальной ширины полосы, что вызывает небольшие повышения при вычислении значения AIC в каждой итерации. Для отчета используется значение AIC финальной модели, которое приводится в разделе информации о диагностике модели.
Суммарная статистика ширины полосы
В разделе Суммарная статистика ширины полосы показаны значения, используемые для оценки того, является ли каждая независимая переменная значимой в каждой локальной модели. Эти показатели статистики включают размер оптимальной окрестности (число соседей или ширина полосы) МГВР, эффективное число параметров, скорректированный уровень значимости (альфа) и скорректированное критическое значение псевдо-t-статистики. Эти значения используются для создания полей, связанных со статистической значимостью каждой независимой переменной в выходных объектах. Скорректированное значение альфа вычисляется делением уровня достоверности (0.05) на эффективное число параметров; это определяет групповую вероятность ошибки (FWER) значимости независимых переменных. Скорректированное значение альфа используется как уровень значимости в двустороннем t-критерии с числом эффективных степеней свободы.
Выходные объекты
Инструмент создает класс объектов, который включает результаты локальных проверок для каждого объекта. Эти проверки включают невязки регрессии, нормированные невязки, прогнозированные значения зависимой переменной, отрезок на координатной оси, коэффициенты независимых переменных, стандартные ошибки коэффициентов, псевдо-t-статистики коэффициентов, значимость коэффициентов, влияние, расстояние Кука, локальный R2 и число обусловленности. Выходные объекты добавляются на карту как слой, и символы присваиваются по значениям стандартизированных невязок. Положительные значения невязок указывают на то, что значение зависимой переменной выше, чем прогнозируемое значение (прогноз занижен), а отрицательные значения указывают на то, что значение зависимой переменной ниже прогнозируемого (прогноз завышен). Для дополнительной информации об этих полях и проверках см. Как работает инструмент Географически взвешенная регрессия.
Диаграммы
В панель Содержание добавляются следующие диаграммы:
- Отношения между переменными — матрица точечной диаграммы, с одной зависимой переменной и до девяти независимых переменных, которая показывает корреляцию между зависимой переменной и каждой независимой переменной, а также корреляции для каждой пары независимых переменных. Сильно выраженная корреляция между парой говорит о мультиколлинеарности.
- Распределение нормированных невязок - гистограмма распределения стандартизированных невязок. Нормированные невязки должны соответствовать нормальному распределению со средним значением - ноль, а среднеквадратическим отклонением - 1.
- Нормированные невязки и Прогнозируемые значения — точечная диаграмма сравнения нормированных невязок в сравнении с соответствующими прогнозируемыми значениями. Диаграмма должна свидетельствовать о случайном распределении и не выявлять трендов или закономерностей.
Дополнительные выходные данные
Следующие дополнительные опции можно указать в ниспадающих меню Опции прогнозирования и Дополнительные опции.
- Выходные прогнозированные объекты — класс объектов с прогнозируемыми значениями зависимой переменной в местоположениях, указанных в параметре Прогнозируемые местоположения.
- Выходная таблица окрестности — указывается таблица для сохранения информации из разделов сообщений Суммарная статистика для оценок коэффициентов и Сводка независимых переменных и окрестностей.
- Рабочая область растровых коэффициентов — указывается рабочая область (директория или база геоданных) куда сохраняются растры коэффициентов. Эти растровые поверхности коэффициентов помогают понять пространсвтенную вариабельность коэффициентов.
Мультиколлинеарность
Мультиколлинеарность возникает, когда две или более переменных демонстрируют сильно выраженную корреляцию в модели регрессии. Она может возникнуть в моделях МНК, ОЛР, ГВР и МГВР. Мультиколлинеарность может оказать негативное влияние на оценки коэффициентов и оптимальные окрестности, так как если независимые переменные коррелируют, их информация дублируется, и модель регрессии не может выявить влияние каждой из этих переменных. В умеренных случаях вычисленные оценки коэффициентов могут быть смещенными и с высокой степенью неопределенности. В экстремальных случаях построение модели может не получиться. В следующем примере показана матрица точечных диаграмм из трех переменных, которые высоко коррелируют друг с другом, и модель регрессии, где они используются их в качестве независимых переменных, обнаружит наличие мультиколлинеарности.
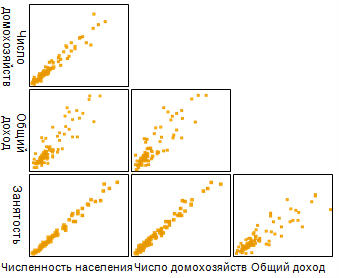
Идентификация и предотвращение мультиколлинеарности в МГВР
В МГВР мультиколлинеарность может возникнуть в нескольких ситуациях, включая следующее:
Для одной из независимых переменных пространственная кластеризация выражена. Так как МГВР подгоняет локальные регрессионные модели, если у объекта и всех его соседей приблизительно совпадают значения независимой переменной, может появиться мультиколлинеарность.
Чтобы предотвратить эту ситуацию, нанесите на карту каждую из независимых переменных и идентифицируйте переменные с небольшим количеством возможных значений или где идентичные переменные показывают пространственные кластеры. Если вы наблюдаете такие случаи в переменных, подумайте о том, чтобы удалить их из модели или использовать возможность увеличения диапазона значений. Переменную с информацией о числе комнат, например, лучше представить как число комнат на квадратный фут.
Две или более независимых переменных демонстрируют сильно выраженную корреляцию глобальном масштабе.
Запустите глобальную модель, используя Обобщенную линейную регрессию и проверьте значение Фактора, увеличивающего дисперсию (VIF) для каждой независимой переменной. Если значения фактора, увеличивающего дисперсию высокие, 7.5, и выше, глобальная мультиколлинеарность может не допустить запуск МГВР. В этом случае можно сделать вывод об избыточных переменных, и рассмотреть возможность исключения их из модели или комбинирования тех переменных с другими независимыми переменными для увеличения вариабельности значений.
Указанная окрестность очень мала.
Мультиколлинеарность так же возникать для нескольких независимых переменных одновременно, и это происходит, когда линейные комбинации некоторых независимых переменных выраженно коррелируют с линейными комбинациями других независимых переменных. Это характерно для окрестностей, в которых небольшое число соседей. Для проверки изучите локальное число обусловленности в выходном классе объектов. Высокое значение числа обусловленности указывает на нестабильность результатов вследствие локальной мультиколлинеарности. Если это произошло, перезапустите модель, используя большее число соседей или диапазон расстояния. Как правило, не стоит доверять результатам для объектов с числом обусловленности более 30, или равным 0. Для шейп-файлов, нулевые значения обозначаются равными 1.7976931348623158e+308. Число обусловленности масштабируется с поправкой на количество независимых переменных в модели, что позволяет вам напрямую сравнивать числа обусловленности между моделям с разным количеством независимых переменных.
Такая проверка поможет выявить мультиколлинеарность, но не поможет решить проблему.
Оценки коэффициентов и ширины полосы
Для всех методов выбора окрестности, кроме Градиентного поиска коэффициенты независимых переменных и ширина полосы окрестности оцениваются с помощью процедуры под названием обратная подгонка (Breiman et al. 1985). Исходно разработанная для оценки параметров обобщенных аддитивных моделей, процедура проходит через независимые переменные, одну за другой, и использует функцию сглаживания для калибровки коэффициентов, сохраняя при этом все остальные независимые переменные постоянными. Этот процесс повторяется для всех независимых переменных, пока значения коэффициентов не стабилизируются и не будут меняться после успешной итерации.
Применяемая к МГВР (Fotheringham et al. 2017) функция сглаживания представляет собой одномерную модель ГВР, которая строит регрессию на основании ранее рассчитанного прогноза скорректированных невязок по одной независимой переменной (рассматривая все остальные независимые переменные как константы). Эта модель ГВР использует тот же метод выбора окрестности (Золотой поиск, интервал вручную или определенный пользователем) для оценки пространственного масштаба независимой переменной. См. раздел Дополнительные ресурсы для подробного описания процедуры.
Алгоритм обратной подгонки должен начинаться с начальных значений коэффициентов. Эти начальные значения оцениваются моделью ГВР для всех независимых переменных. Если эта модель не запускается из-за мультиколлинеарности, применяется модель МНК. Если не удалось выполнить схождение после 25 итераций, будут использованы значения коэффициентов последней итерации.
Градиентный поиск
Опция выбора окрестности Градиентный поиск лучше всего подходит для оценки оптимальной ширины полосы МГВР, где не используется обратная подгонка. Основные преимущества Градиентного поиска - улучшенное время обработки и более эффективное расходование памяти. Этот метод представляет собой алгоритм оптимизации второго порядка, который использует градиент и матрицу Гессиана для минимизации AIC относительно пространственного масштаба независимых переменных. Вместо обновления параметра одной независимой переменной в каждом шаге итерации, параметры всех независимых переменных обновляются одновременно путем снижения градиента в направлении самого резкого изменения, скорректированного кривизной AIC.
Результаты золотого поиска и градиентного поиска обычно похожи. На следующем изображении показана поверхность истинного коэффициента вместе с поверхностью предполагаемого коэффициента для Золотого поиска и Градиентного поиска. Обратите внимание, что все поверхности совпадают и оценка истинной поверхности точна.
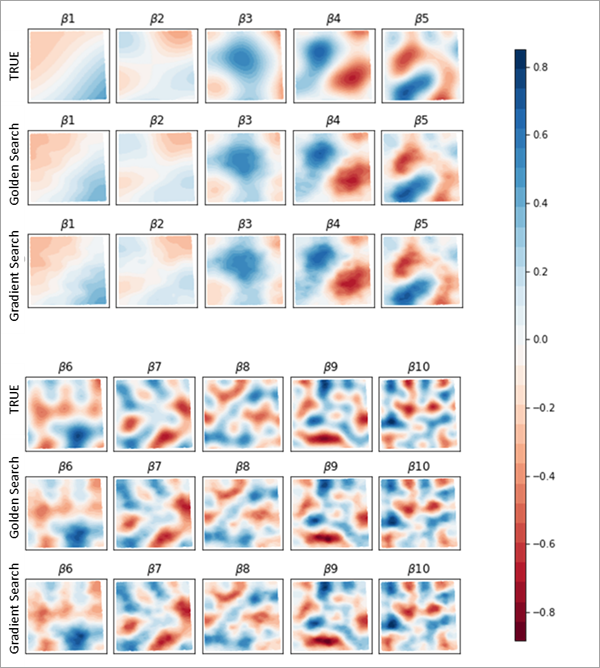
На рисунке ниже сравнение времени запуска для Градиентного поиска и Золотого поиска для разных количеств независимых переменных и разных размеров наборов данных. Время обработки для Градиентного поиска составляет приблизительно половину времени обработки Золотого поиска для того же количества независимых переменных.
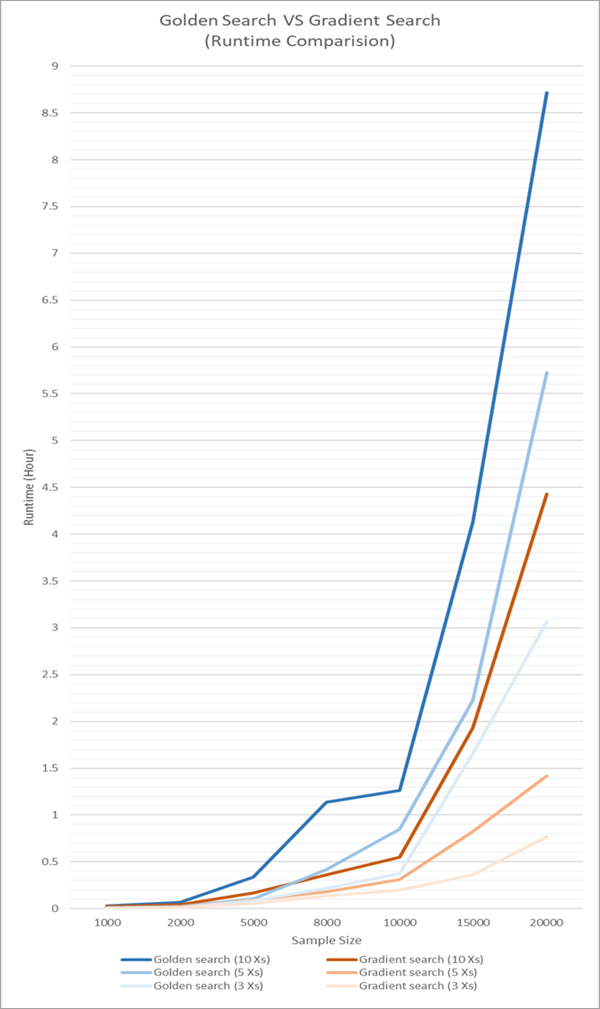
На рисунке ниже сравнивается использование памяти для Градиентного поиска и Золотого поиска Использование памяти при Золотом поиска резко возрастает (квадратичный рост) при увеличении размера выборки, а использование памяти при Градиентном поиске не зависит от размера выборки.
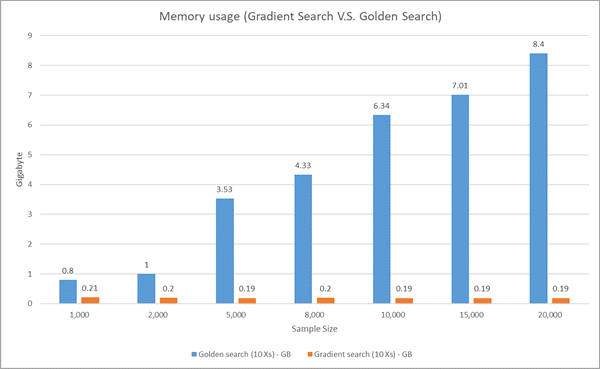
На рисунке ниже сравнивается значение AIC для Градиентного поиска и Золотого поиска. Точность этих методов очень близка, но при Золотом поиске достигается значения AIC чуть ниже (то есть оценка чуть более точная), чем при Золотом поиске.
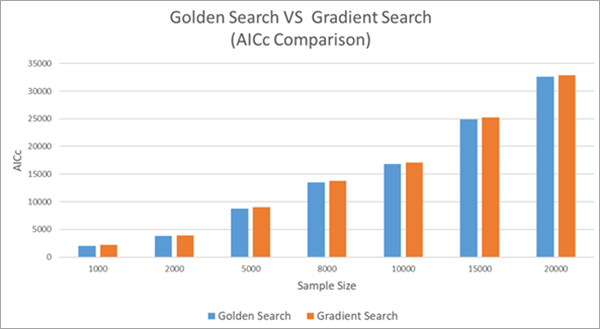
Дополнительные ресурсы
Более подробную информацию смотрите в разделе:
- Breiman, L., and J. H. Friedman. 1985. "Estimating optimal transformations for multiple regression and correlations (with discussion)." Journal of the American Statistical Association 80, (391): 580–619. https://doi.org/10.2307/2288473. JSTOR 2288473.
- Brunsdon C., A. S. Fotheringham, and M. E. Charlton. 1996. "Geographically weighted regression: A method for exploring spatial nonstationarity." Geographical Analysis 28: 281–298.
- Conn, A.R., N.I.M. Gould, and P.L. Toint. 2000. "Trust Region Methods." Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9780898719857.
- da Silva, A. R., and A. S. Fotheringham. 2016. "The multiple testing issue in geographically weighted regression." Geographical Analysis 48(3), 233–247. https://doi.org/10.1111/gean.12084.
- Fotheringham, A. S., W. Yang, and W. Kang. 2017. "Multiscale geographically weighted regression (MGWR)." Annals of the American Association of Geographers 107: 1247–265. https://doi.org/10.1080/24694452.2017.1352480
- Oshan, T. M., З. Li, W. Kang, L. J. Wolf, and A. S. Fotheringham. 2019. "mgwr: A Python implementation of multiscale geographically weighted regression for investigating process spatial heterogeneity and scale." ISPRS International Journal of Geo-Information 8: 269.
- Yu, H., A. S. Fotheringham, Z. Li, T. Oshan, W. Kang, and L. J. Wolf. 2020. "Inference in multiscale geographically weighted regression." Geographical Analysis 52: 87–106.
- Zhou, X., R. Assunção, H. Shao, M. Janikas, C. Huang, and H. Asefaw. 2023. "Gradient-based optimization for Multi-scale Geographically Weighted Regression." (under review)
Связанные разделы
- Обзор группы инструментов Моделирование пространственных отношений
- Мультимасштабная географически взвешенная регрессия (МГВР)
- Метод наименьших квадратов (МНК)
- Основы регрессионного анализа
- Как работает Географически взвешенная регрессия
- Исследовательская регрессия
- Классификация на основе леса и регрессия, регрессия с бустингом