Нечеткую логику можно использовать в качестве метода анализа наложения при решении традиционных задач анализа наложения, таких как выбор места и модели пригодности.
Предпосылкой использования нечеткой логики является существование неточностей в атрибутах и геометрии пространственных данных. Нечеткая логика предоставляет методы для устранения обоих типов неточностей, но нечеткая логика в анализе наложения фокусируется на неточностях в атрибутивных данных. Две основные области возникновения неточностей в атрибутивных данных – определение классов и измерение явления. Оба эти источника неточностей, особенно в определении классов, могут привести к ошибкам отнесения ячеек к определенным классам.
Определение классов в классификации и ошибочное распределение явления по классам могут повлиять на принятие решений. Инструменты Нечеткого наложения помогают ответственным лицам принимать решения относительно этих неточностей. Нечеткая логика фокусируется на моделировании неточностей границ классов.
Инструменты Взвешенное наложение и Взвешенная сумма основываются на четких множествах, где каждая ячейка либо относится к классу, либо нет. Нечеткая логика специально предназначена для ситуаций, когда границы между классами размыты. В отличие от четких множеств, нечеткая логика не зависит от принадлежности к классу или нахождению вне его; она определяет, насколько вероятно, что явление является членом множества (или класса). Нечеткая логика основана на теории множеств; следовательно, вы определяете возможности, а не вероятности.
Например, в модели пригодности жилья, если уклон является одним из входных критериев, каждому значению уклона будет присвоено значение от 0 до 1, в зависимости от того, возможно ли это значение уклона отнести к множеству пригодности для зданий (или классу). Значение 1 указывает на полную уверенность в том, что значение находится в множестве пригодности, а 0 указывает на полную уверенность в том, что его нет в множестве. Все остальные значения представляют собой некоторый уровень возможности принадлежности, причем более высокие значения указывают на большую возможность принадлежности. Процесс преобразования исходных входных значений в шкалу возможности принадлежности от 0 до 1 называется процессом формирования нечеткости (фаззификация). Каждый критерий модели, например экспозиция, расстояние до дорог и тип землепользования, будет преобразован в нечеткое множество. Инструмент Нечеткое множество используется для преобразования данных в шкалу возможности от 0 до 1.
Для определения местоположений, которые лучше всего соответствуют всем критериям, то есть имеют высокую возможность принадлежности ко всем множествам, используется инструмент Нечеткое наложение. При комбинировании нескольких критериев инструмент Нечеткое наложение исследует возможность того, что ячейка является членом каждого множества, определяемого разными критериями. Например, какова возможность того, что определенное местоположение имеет благоприятную пригодность по уклону, экспозиции и расстоянию до дорог?
Таким образом, двумя основными этапами нечеткой логики для анализа наложения являются фаззификация, или процесс нечеткого множества, и анализ нечеткого наложения. Эти два шага коррелируют с этапами переклассификации/преобразования и добавления/объединения, соответственно, в общем процессе наложения.
Часто неясно, принадлежит ли что-то к классу или нет, и это субъективно. В человеческом языке эти неточности квалифицируются с помощью модификаторов, таких как очень, слегка и умеренно. Нечеткая логика выполняет анализ наложения, больше похожий на естественное человеческое мышление. Все не так однозначно; границы могут быть размыты. Нечеткая логика — это не анализ неопределенности данных, а исследование неточностей в границах классов.
В следующих разделах обсуждаются вопросы классификации данных, процесса нечеткого множества и выполнения анализа нечеткого наложения. Далее также обсуждается сравнение нечеткой логики с методами анализа бинарного и взвешенного наложения и то, как нечеткая логика интегрируется в общий процесс наложения.
Классификация данных и нечеткая логика
Чтобы описать или упорядочить явления, вы обычно распределяете их по классам. Категория землепользования, тип почвы, оценка пригодности, класс дороги и тип растительности — все это примеры классов. В четких множествах принадлежность является бинарной, и явление либо принадлежит классу, либо нет. Границы классов четкие. Но из-за неточности мышления, неоднозначности правил категоризации, расплывчатости и амбивалентности границы между классами не всегда четкие.
Например, если явление, которое вы изучаете, зависит от роста людей в группе, вы можете начать с группировки разных людей в классы на основе их роста. Вы можете начать с трех классов: низкий, средний и высокий. Вы должны установить границы для классов. Например, невысокий человек может быть ростом 5 футов (1,524 метра) или ниже, высокий человек может быть ростом 6 футов (1,8288 метра) и выше, а человек среднего роста может быть от 5 до 6 футов (1,6764 и 1,8288 метра). Если человек имеет рост 6 футов (1,8288 метра), он будет отнесен к классу высоких людей. Если рост человека 5 футов 11 дюймов (1,8034 метра), он будет классифицирован как средний. При разнице в росте всего 1 дюйм (0,0254 метра) двух людей помещают в два разных класса. Такое же различие будет для участников группы, рост одного из которых 5 футов 1 дюйм (1,5494 метра), а рост другого - 6 футов 6 дюймов (1,9812 метра). Из-за грубости классификации все отношения между людьми разного роста не могут быть отражены.
Чтобы более точно отобразить отношения между ростом различных людей, можно добавить больше классов. Например, могут быть добавлены еще два класса: низкий - 4 фута 10 дюймов (1,4732 метра) или меньше, ниже среднего - от 4 футов 10 дюймов (1,4732 метра) до 5 футов 4 дюймов (1,6256 метра), средний - от 5 футов 4 дюймов (1,6256 метра) до 5 футов 10 дюймов (1,778 метра), выше среднего - от 5 футов 10 дюймов (1,778 метра) до 6 футов 4 дюйма (1,9304 метра), высокий - более 6 футов 4 дюйма (1,9304 метра). Благодаря такому уточнению классов, можно более точно отразить отношения между людьми разного роста.
Для дальнейшего уточнения можно добавить еще больше классов. Независимо от того, сколько классов добавлено, все равно будет существовать обобщение отношений между людьми разного роста. Есть явления, которые нельзя отнести к строго определенным классам. Иногда бывает трудно сгруппировать реальный мир в дискретные классы.
Очевидно, что определение границ классов может быть субъективным и меняться вместе с определением явления. В определенных ранее классах роста предполагается, что люди были взрослыми, скорее всего, и мужчинами, и женщинами. Определения классов, возможно, придется изменить, если группа полностью состоит из женщин. Границы класса могут измениться еще больше, если группа состоит из детей или включает в себя детей.
Определение классов и характеристики явления диктуют, как представлять моделируемое явление. Погрешность измерений еще больше усугубляет проблему классификации. Если процедура замера роста людей имеет точность плюс-минус 1 дюйм (0,0254 метра), неточность измерения может изменить класс, к которому будет отнесено явление.
Нечеткая логика моделирует эту неточность в процессе классификации. В нечеткой логике классы определяются как множества. Есть понимание идеального значения принадлежности к множеству, например, идеальное значение уклона в модели пригодности жилья. По мере того, как значения удаляются от идеала, уровень ясности снижается до определенного момента, когда становится ясно, что значение уже не является членом множества (например, слишком крутой уклон, чтобы вести строительство).
Например, в вышеприведенном примере с ростом, если вы оставите три класса роста людей — низкий, средний и высокий — эти три класса в нечеткой логике могут перекрываться.
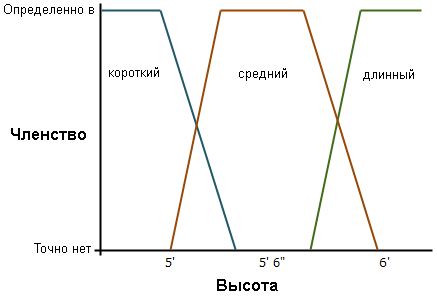
На изображении выше полная принадлежность к каждомму классу это
- Низкий: < 5 футов (1,524 метра)
- Средний: от 5 футов 3 1/2 дюйма (1,6129 метра) до 5 футов 8 1/2 дюйма (1,7399 метра)
- Высокий: > 6 футов (1,8288 метра)
Для множества низких значений (или класса) любой, кто имеет рост 5 футов (1,524 метра) или ниже, определенно входит в множество малых значений и получает 1. Любой рост более 5 футов (1,524 метра) и менее 5 футов 3 1/2 дюйма (1,6129 метра) находится между малым и средним множествами (или классами). Рост от 5 футов (1,524 метра) до 5 футов 1 3/4 дюйма (1,6193 метра), скорее всего, попадает в низкое множество. Рост более 5 футов 1 3/4 дюйма (1,6193 метра) и менее или равный 5 футам 3 1/2 дюйма (1,6129 метра), может относиться к низкому множеству, но с большей вероятностью относится к среднему множеству.
Процесс формирования нечеткости (фаззификация) обычно реализуется через заранее определенные функции с помощью инструмента Нечеткое множество.
Нечеткое множество
Процесс фаззификации характеризует неточность классов для явлений, не попадающих в четко очерченные границы.
Фаззификация преобразовывает исходные значения явления в возможность их принадлежности к определенному множеству. Определенное множество может отражать пригодность, или нахождение на благоприятном расстоянии от чего-либо, или возможность нахождения определенного минерала. Исходные значения явления переклассифицируются в эту непрерывную принадлежность с помощью предопределенных функций нечеткого множества или с помощью любых других методов переклассификации.
В процессе фаззификации определяется идеальное определение принадлежности к множеству. Каждому значению явления, имеющему наиболее центральное значение относительно ядра определения множества, будет присвоено значение 1. Тем значениям, которые точно не являются частью множества, присваивается 0. Значения между двумя крайними значениями попадают в переходную зону множества, границу. По мере удаления значений от идеала или центра множества им присваивается уменьшающееся значение по непрерывной шкале от 1 до 0. По мере того, как присваиваемые значения уменьшаются, исходное значение явления имеет меньше шансов быть членом этого множества.
Значение фаззификации 0,5 является точкой перехода. Любое нечеткое значение больше 0,5 подразумевает, что исходное значение явления является частью множества. Когда значения фаззификации опускаются ниже 0,5, менее вероятно, что исходное значение явления участвует в множестве; значения могут не входить в множество.
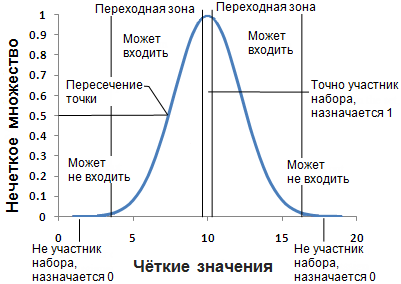
Ширина переходной зоны зависит от моделируемого явления, того, что известно о явлении, определения множества и точности измерений. Изменение параметров функции фаззификации может определить характеристики переходной зоны. На изображении ниже нечеткая функция Гаусса показана тремя различными кривыми, полученными в результате изменения параметров функции.
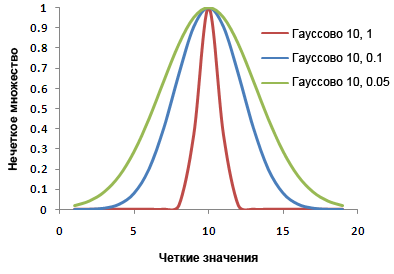
Параметры служат модификаторами для определения множества. Модификаторы характеризуют потенциальное перекрытие или компромиссный вариант между множествами.
Процесс фаззификации выполняется для каждого критерия в анализе наложения.
Методы нечеткого наложения
Для анализа взаимосвязей и взаимодействия множеств всех критериев в модели наложения используются методы нечеткого наложения. Поскольку процесс фаззификации основан на степени принадлежности множеству, методы наложения описывают взаимосвязь неточностей в принадлежности множеств. Методы нечеткого наложения основаны на теории множеств. Теория множеств — это математическая дисциплина, определяющая отношение принадлежности явления к конкретным множествам. В нечетком наложении множество обычно соответствует классу.
Доступные методы наложения нечетких множеств: нечеткое И, нечеткое Или, нечеткое Произведение, нечеткая Сумма и нечеткая Гамма. Каждый из этих методов описывает отношение принадлежности ячейки к входным множествам. Например, тип нечеткого наложения И создает выходной растр, в котором каждому значению ячейки присваивается минимальное назначенное нечеткое значение для каждого из множеств, к которым принадлежит местоположение ячейки. Если анализ наложения представляет собой модель пригодности жилья, и каждый критерий был преобразован в нечеткое множество, отражающее его принадлежность к множеству пригодности, нечеткое наложение И идентифицирует наименьшую возможность принадлежности ячейки к одному из множеств пригодности различных критериев.
Тип нечеткого наложения Или возвращает максимальное значение пересечения множеств. То есть в модели пригодности жилья максимальная потенциальная принадлежность (наивысшее значение пригодности) для каждой ячейки оценивается по множеству критериев.
Наложение двоичной, взвешенной и нечеткой логики
Часто в описаниях нечеткой логики для анализа наложений ее сравнивают с бинарным анализом наложений. В бинарном анализе наложения для всех критериев оценивается принадлежность каждой ячейки к указанному классу. Как уже было сказано, часто бывает сложно определить четкие границы классов и окончательно отнести ячейки к конкретным классам. В бинарном анализе при построении модели пригодности жилья каждой ячейке присваивается значение пригодности (1) или непригодности (0) для каждого критерия. В процессе наложения местоположения, которым присвоено значение 1 для всех входных критериев, считаются потенциально подходящими местоположениями.
Ограничения подхода бинарного анализа наложения включают:
- Если ни одно местоположение не отвечает всем критериям, второго по степени пригодности варианта не определяется.
- Относительный вес местоположений, отвечающих критериям, отсутствует.
- Рассмотренные выше проблемы, касающиеся процесса классификации.
Анализ взвешенного наложения пытается устранить эти ограничения. Вместо того, чтобы классифицировать каждую ячейку по бинарной шкале в значения 1 или 0, инструмент Взвешенное наложение присваивает каждой ячейке значение по заданной непрерывной шкале, например, шкале от 1 до 10, где 10 является наиболее предпочтительным для каждого критерия. Непрерывная шкала обеспечивает больше градаций классов, что позволяет точнее отображать явление. Для каждого критерия каждой ячейке присваивается значение по шкале от 1 до 10. Затем все переклассифицированные критерии суммируются. Расположение ячеек с наибольшими суммарными значениями является наиболее предпочтительным по входным критериям. Чем больше благоприятных критериев для каждого из входных данных, тем лучше.
Нечеткое наложение и взвешенное наложение больше похожи друг на друга, чем на бинарное наложение; однако они строятся на разных принципах. Нечеткое наложение основано на теории множеств, а взвешенное наложение основано на линейных комбинациях. Оба метода преобразуют исходные значения. В нечетком наложении преобразование определяет возможность принадлежности к множествам, тогда как взвешенное наложение выполняется по шкале относительных предпочтений. Поскольку эти два метода уникальны, инструменты для выполнения анализа по нескольким критериям не являются взаимозаменяемыми.
Нечеткая логика и общий процесс анализа наложения
Анализ наложения нечеткой логики следует общим шагам анализа наложения, но с большим вниманием к одним шагам и меньшим к другим, а также с иным смыслом значений присвоенных чисел, чем у других методов анализа наложения.
Общие шаги анализа наложения:
- Определите проблему.
- Разбейте проблему на подмодели.
- Определите значащие слои.
- Переклассифицируйте или преобразуйте данные в слое.
- Взвесьте входные слои.
- Добавьте или комбинируйте слои.
- Анализируйте.
Как для любого анализа наложения, шаги с 1 по 3 сохраняются и для анализа нечеткой логики. Поскольку нечеткая логика основана на множествах, значение переклассифицированных значений (шаг 4) и методы анализа, которые можно использовать для объединения нескольких критериев (шаг 6), делают нечеткую логику уникальной по сравнению с другими подходами к анализу наложения.
В следующих разделах обсуждается, чем для нечеткой логики отличаются шаги с 4 по 7.
Переклассифицируйте или преобразуйте данные в слое
Входные данные переклассифицируются или трансформируются по шкале от 0 до 1, выявляя возможность принадлежности к заданному множеству. Этот процесс переклассификации или фаззификации реализуется с помощью инструмента Нечеткое множество. Чтобы помочь в этом процессе преобразования, была разработана серия функций множеств. Доступны следующие функции: нечеткая Гауссова, нечеткая Large, нечеткая Linear, нечеткая MSLarge, нечеткая MSSmall, нечеткая Near и нечеткая Small. Каждая функция множества преобразует данные определенным образом, чтобы отразить взаимосвязь явления.
Вес входных слоев
Поскольку нечеткая логика основана на теории множеств, и вы определяете, принадлежит ли конкретное местоположение одному или нескольким множествам, взвешивание не имеет смысла. Увеличение веса одного фактора относительно другого не может увеличить возможность принадлежности к одному множеству или комбинации нескольких множеств. Местоположение либо является членом множества, либо нет (со всеми промежуточными степенями). В анализе нечеткого наложения взвешивание критериев неприменимо.
Добавьте или объедините слои
На этапе добавления или объединения нечеткая логика исследует взаимодействие возможностей явления для нескольких множеств, в отличие от взвешенного наложения и взвешенной суммы, которые основаны на идее о том, что более благоприятные элементы означают лучший результат.
Для нечеткого наложения существуют специальные методы исследования этой относительной связи и количественной оценки взаимодействия. Методами комбинирования являются нечеткое И, нечеткое Или, нечеткое Произведение, нечеткая Сумма и нечеткая Гамма. Каждый из этих методов основан на теории множеств и специфичен для анализа нечетких наложений.
Анализ
Как и в любом анализе наложения, от вас зависит анализ и интерпретация результатов. Однако из-за различного смыслового значения переклассифицированных значений и методов наложения, лежащих в основе каждого подхода наложения, может потребоваться использование разных механизмов для измерения достоверности результатов.