Пространственные данные часто обладают пространственной автокорреляцией, когда у близких друг к другу наблюдений схожие значения. Если проигнорировать это в моделях регрессии, можно получить смещенные оценки и неверные выводы.
Инструмент Пространственная авторегрессия разработан для решения этих задач с помощью пространственной модели регрессии, которая явно учитывает пространственную зависимость. Этот инструмент может выполнять обычную регрессию по методу наименьших квадратов или одну из следующих глобальных моделей пространственной регрессии: модель пространственного лага, модель пространственной ошибки и пространственную комбинированную модель авторегрессии. Вы можете указать модель, которую будет использовать инструмент, или он определит наиболее подходящую модель, выполнив набор диагностических тестов на зависимых и независимых переменных.
Цель этих моделей регрессии заключается в обеспечении точности выводов регрессионных моделей при наличии пространственной зависимости. С моделью пространственной регрессии вы можете быть более уверены в оценках, а также сможете оценить эффекты пространства в ваших моделях.
Возможное применение
Инструмент Пространственная авторегрессия можно использовать для учета пространственной зависимости в моделях двумя основными способами.
Во-первых, модель пространственного лага полезна для анализа пространственных эффектов перетекания, например:
- Общественное здоровье и эпидемиология - изучение распространения болезней или вирусов с учетом пространственной зависимости.
- Криминалистика - изучение скоплений и распространения преступлений, включая эффекты окрестностей.
Во-вторых, модель пространственной ошибки может предоставить несмещенные оценки моделей, учтя пространственную зависимость в независимых переменных, например:
- Социально-экономический анализ - оценка уровня образования с контролем факторов пространственной корреляции в независимых переменных.
- Цены жилья - контроль неизмеренных пространственных факторов, влияющих на цену собственности, что дает более четкое представление о ключевых переменных модели.
Типы моделей
Инструмент Пространственная авторегрессия может оценить три возможных глобальных модели пространственной регрессии, каждая из которых учитывает пространственную зависимость по-разному. Регрессия по Методу наименьших квадратов выполняется, если ни одна из трех моделей пространственной регрессии не определена как подходящая на основе различных диагностик.
Модель пространственной ошибки
Модель пространственной ошибки (SEM) разработана для решения ситуаций, когда в невязках модели регрессии присутствует пространственная автокорреляция. Для SEM пространственная зависимость рассматривается как нежелательный параметр. Нежелательный параметр – это параметр, который необходимо учитывать, чтобы были сделаны верные выводы. Модель SEM определена следующей формулой:
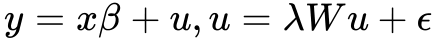
Она похожа на формулу регрессии по методу наименьших квадратов, в которой зависимая переменная (y) предсказывается набором независимых переменных (x) и коэффициентов (β). Однако компонент невязки (u) моделируется другим уравнением регрессии. Эта вторая регрессия предсказывает невязку с помощью параметра пространственной авторегрессии λ (лямбда) и матрицы пространственных весов (W), вместе с ее собственным компонентом невязки (ε). Параметр лямбда определяет силу пространственной зависимости в компоненте ошибки и измеряет, как компонент ошибки одного местоположения влияет на компоненты ошибки его соседей.
SEM работает, выполняя фильтрацию пространственной автокорреляции из каждой переменной в модели, а затем выполняя регрессию на пространственно отфильтрованных переменных. В результате пространственная автокорреляция не так сильно влияет на оценки коэффициентов каждой переменной.
Модель пространственного лага
В отличие от SEM, которая рассматривает пространственную зависимость как нежелательную величину, модель пространственного лага (SLM) использует ее в качестве независимой переменной. Модель пространственного лага используется, если у зависимой переменной присутствует большое количество пространственной автокорреляции, и виден пространственный эффект перетекания (это означает, что изменения в одной области вызывают изменения в соседних областях). Модель SLM определена уравнением:

Зависимая переменная предсказывается как независимыми переменными, так и ее собственным пространственным лагом (Wy). Параметр пространственной авторегрессии ρ (ро) измеряет силу влияния соседей местоположения на значение зависимой переменной (y). Более высокие оцененные значения параметра ρ означают процесс диффузии, при котором значения на некотором местоположении влияют на значения на соседних местоположениях. Но дальше соседи могут повлиять на исходное местоположение, вызывая цикл обратной связи.
Пространственная комбинированная модель авторегрессии
Пространственная комбинированная модель авторегрессии (SAC) включает параметры пространственной авторегрессии λ и ρ из моделей пространственной ошибки и пространственного лага соответственно.
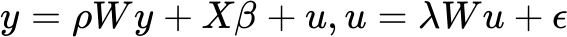
В этом случае моделируется пространственная зависимость как компонента ошибки, так и в пространственном лаге для зависимой переменной. Модель SAC можно использовать для определения пространственных эффектов перетекания в зависимой переменной, учитывая при этом пространственную зависимость в компоненте ошибки.
Выбор подходящей модели
По умолчанию инструмент выберет наиболее подходящую модель на основе набора статистических тестов, который называется тестом множителей Лагранжа (LM) (также известный как оценка Рао). Процесс выбора в основном соответствует рабочему процессу, описанному Anselin и Rey (2014).
Критерии выбора модели показаны в блок-схеме ниже:
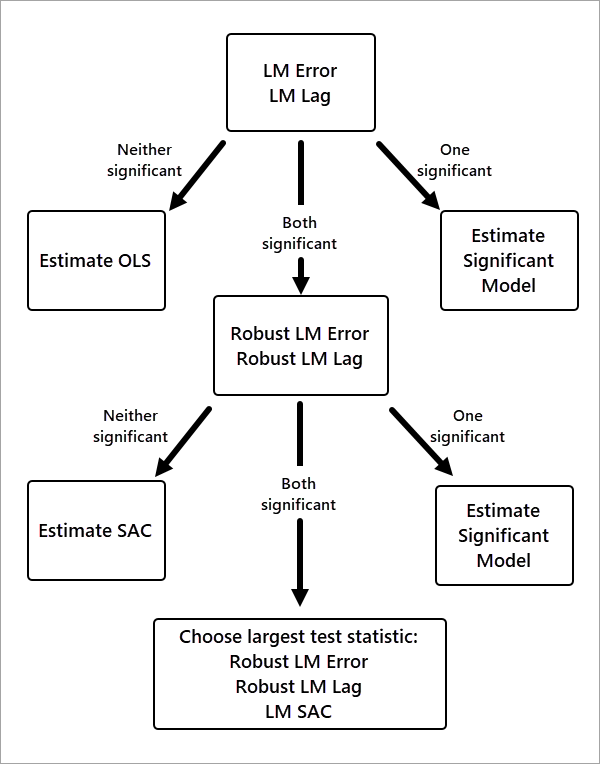
Сначала выполняется тест LM для моделей пространственного лага (LM Lag) и пространственной ошибки (LM Error). Если ни один из тестов не является статистически значимым (p-значение больше 0.05), в пространственной модели нет необходимости, и выбирается модель OLS. Если один из тестов является значимым, выбирается соответствующая модель.
Если оба теста LM Lag и LM Error значимы, выполняются их строгие версии. Это тесты Robust LM Lag и Robust LM Error, у которых более строгая версия теста. Если один из тестов является значимым, выбирается соответствующая модель.
Если оба строгих теста являются значимыми, выполняется тест LM для модели SAC. Если все три теста значимы, выбирается модель с наибольшей статистикой теста.
В редком случае, когда тесты LM Lag и LM Error являются значимыми, но ни один из строгих тестов не является, выбирается модель SAC.
Важно отметить, что тесты LM - это подход на основе данных к выбору модели. Они не гарантируют хорошую модель, которая подойдет. Просмотрите диагностику и учтите теоретические предположения модели.
Выходные данные инструмента
Основным выходом инструмента является некоторое количество таблиц в сообщениях геообработки, а также выходной класс объектов и диаграмма, визуализирующая невязки модели.
Выходные объекты
Выходной класс объектов инструмента содержит поля зависимой переменной, независимой переменной, предсказанного значения зависимой переменной, невязки и стандартизированной невязки, пространственного лага невязки и количества соседей каждого объекта.
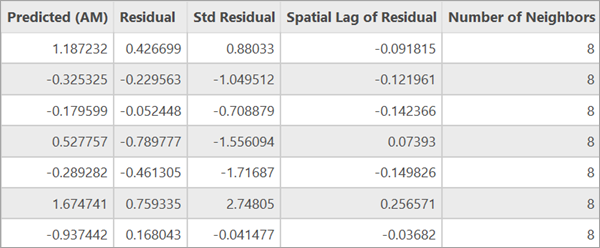
При добавлении слоя на карту объекты будут помечены их стандартизированными невязками. Визуализация стандартизированных невязок может помочь в определении закономерностей в кластеризации компонента ошибки.
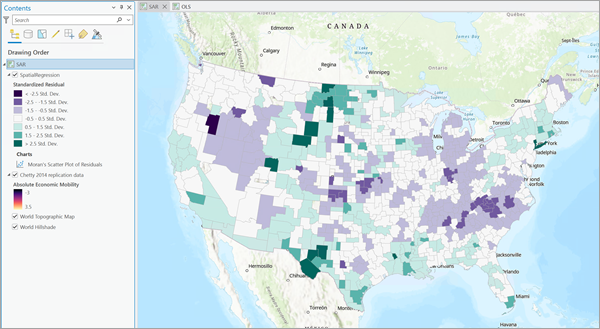
Невязки обозначены цветом от темно-фиолетового до темно-зеленого. Местоположения, обозначенные зеленым, имеют положительную невязку, что означает, что модель переоценила значение. Аналогично, местоположения фиолетового цвета имеют отрицательную стандартизированную невязку. Отрицательная невязка означает, что местоположение недооценено.
Диаграмма рассеяния Морана для невязок
Выходной слой содержит диаграмму рассеяния, которая показывает невязки относительно их пространственного лага. Ось X отображается стандартизированную невязку, а ось Y отображает пространственный лаг стандартизированной невязки. Такой тип диаграммы называют диаграммой рассеяния Морана.

Эту диаграмму можно разбить на четыре квадранта около 0 на осях X и Y. Значения в верхнем правом и нижнем левом квадрантах представляют пространственную автокорреляцию. Это местоположения, значения которых схожи с их соседями: положительные и отрицательные значения соответственно. Верхний левый и нижний правый квадранты представляют местоположения с отрицательной автокорреляцией. В этих местоположениях высокие значения окружены низкими (и наоборот).
Когда невязки распределены равномерно по всем четырем квадрантам, это показывает что пространственная автокорреляция явно не выражена. Такая закономерность ожидается, когда модель регрессии хорошо справилась, и большая часть пространственной автокорреляции была учтена.
Сообщения геообработки
Инструмент предоставляет таблицы в сообщениях геообработки, которые дают информацию о том, как оценена каждая модель:
- Информация о пространственных весах и окрестностях
- Результаты тестов LM
- Сводка результатов модели
- Проверки модели
В некоторых случаях будут отображены также следующие таблицы сообщений:
- Сводка влияния коэффициентов
- Отчет о совпадающих точках
Все таблицы описаны ниже.
Информация о пространственных весах и окрестностях
Модели SEM, SLM и SAC требуют матрицу пространственных весов, которая может значительно повлиять на результаты модели. Таблица Информация о пространственных весах и окрестностях предоставляет сведения о матрице пространственных весов, которая использовалась для подбора модели. В ней указаны тип окрестности, схема присвоения весов, пространственная связность, средний размер окрестности, минимальный размер окрестности и максимальный размер окрестности.
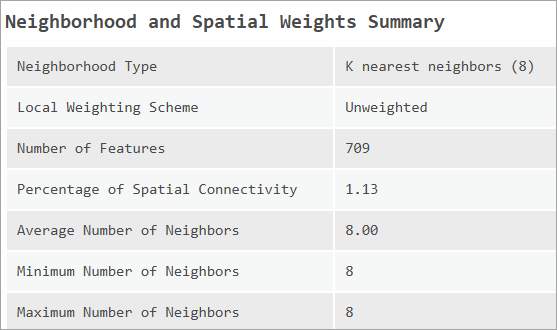
Важно отметить, что инструмент не будет оценивать модель, если матрица пространственных весов слишком сильно связана. Процент пространственной связности - это примерное среднее количество соседей для каждого объекта как процент общего числа объектов. Например, с 500 объектами и пространственной связностью равной 0.1, у каждого объекта в среднем будет около 50 соседей. Если матрица пространственных весов имеет связность 30 процентов или больше, результаты модели окажутся смещенными (Smith, 2009). В этом случае инструмент возвратит ошибку.
Результаты тестов LM
Таблица Результаты тестов LM сообщает диагностики Множителя Лагранжа для каждого теста. Таблица также отображает тип модели, который будет выбран на основе блок-схемы в разделе Выбор подходящей модели выше.

Отчет о совпадающих точках
Совпадающие точки (точки с одинаковыми координатами) могут вызывать различные проблемы в пространственной авторегрессии, например, могут создаваться веса, равные 0, для всех соседей. Если во входных объектах присутствуют совпадающие точки, Отчет о совпадающих точках сообщит общее число объектов, количество уникальных местоположений, а также минимум, максимум и среднее количество совпадающих точек для всех объектов. Также могут отображаться предупреждения и ошибки, вызванные совпадающими точками.

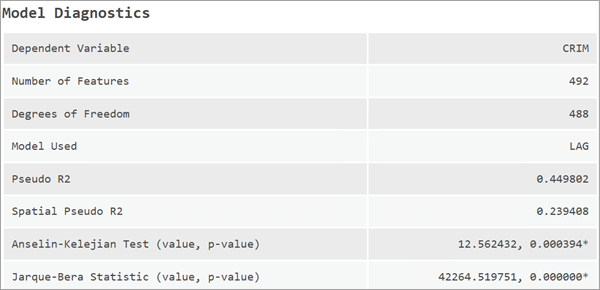
Проверки модели
Таблица Проверки модели отображает важные диагностики, такие как зависимую переменную, количество объектов, степени свободы и модель, которая была использована.

Если оценена модель OLS, выровненный R-квадрат отображен в таблице. Однако для всех пространственных моделей вместо этого отображен псевдо R-квадрат. Для моделей SLM и SAC также отображен пространственный псевдо R-квадрат. Это описано далее.
Дополнительно представлена статистика Жака-Бера. Если статистика значима, это означает, что невязки модели не соответствуют нормальному распределению. Хотя модели оценены с помощью методов, нечувствительных к ненормальности, тест может означать неверную спецификацию модели или наличие выбросов.
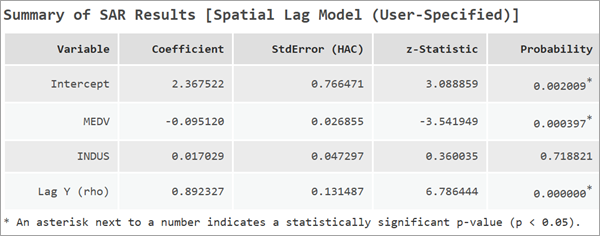
Интерпретация результатов модели пространственного лага
Модель пространственного лага сообщает дополнительный коэффициент под названием Lag Y (ро). Это пространственный лаг зависимой переменной. Коэффициент этой переменной измеряет силу и направление пространственной зависимости зависимой переменной. Значение ро должно быть в диапазоне между -1 и 1. Большие значения Lag Y могут означать сильный процесс пространственной обратной связи.
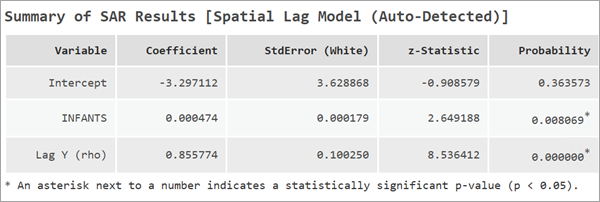
Важно отметить, что изменение независимой переменной в одном местоположении может повлиять на значение зависимой переменной в другом местоположении, это называется пространственным перетеканием. При наличии пространственного перетекания коэффициенты регрессии должны быть интерпретированы вместе с эффектом пространственного перетекания.
Воздействия и эффекты коэффициентов
Помимо коэффициентов регрессии сообщаются величины под названием воздействия. Воздействия помогают измерить эффект пространственного перетекания для всех независимых переменных. Они делятся на прямые, непрямые и полные воздействия. Существуют разные методы вычисления воздействий, и этот инструмент сообщает простые воздействия. Прямые, непрямые и полные воздействия отображены в таблице сообщений Сводка влияния коэффициентов.
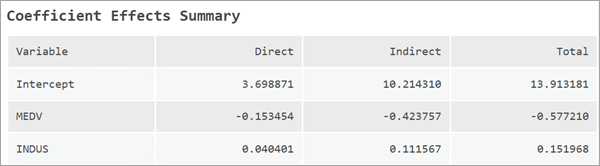
Прямые воздействия измеряют, как сильно единичное изменение независимой переменной влияет на значение зависимой переменной в самом местоположении. В случае простых воздействий это то же значение, что и бета коэффициент.
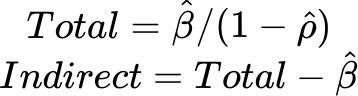
А непрямые воздействия измеряют, как сильно единичное изменение переменной влияет на зависимую переменную в соседних местоположениях. Однако заметьте, что на значение воздействий сильно влияет матрица пространственных весов.
Стандартные ошибки
По умолчанию модель пространственного лага сообщает точные стандартные ошибки. Однако после подбора модели пространственного лага большое количество автокорреляции в невязках может остаться. Тест Анселина-Келеджяна (AK) - это диагностический тест, который используется, чтобы определить, осталось ли значительное количество пространственной зависимости в невязках модели.
Если тест AK является значимым (p-значение меньше 0.05), сообщаются другие меры стандартной ошибки под названием гетероскедастичные и строгие автокорелляционные (HAC) стандартные ошибки. Стандартные ошибки HAC это непараметрический вариант стандартных ошибок, полезный при наличии пространственной автокорреляции.
Стандартные ошибки HAC учитывают пространственное распределение данных с помощью отдельной матрицы пространственных весов. Матрица пространственных весов создается с помощью k ближайших соседей для определения окрестности каждого объекта, включая фокальный объект. Веса каждой окрестности моделируются с использованием треугольного ядра.
Псевдо R-квадрат и пространственный псевдо R-квадрат
Поскольку модель пространственного лага включает пространственный лаг зависимой переменной в качестве независимой переменной, традиционные методы прогнозирования линейной регрессии нельзя использовать. Предсказывание зависимой переменной с использованием ее пространственного лага приводит к излишне самоуверенным оценкам. Чтобы преодолеть это, вычисляется другая мера под названием пространственный псевдо R-квадрат.
Пространственный псевдо R-квадрат вычисляется без пространственного лага зависимой переменной. Вместо этого он использует матрицу пространственных весов и оценку λ для создания предсказанных значений Wy-hat, которые используются вместо Wy в прогнозе.
Предсказанные значения затем используются для вычисления традиционного значения псевдо R-квадрат. Рекомендуется сообщать значение пространственного псевдо R-квадрат вместо псевдо R-квадрат.
Важно отметить, что пространственный псевдо R-квадрат отличается от выровненного R-квадрат, который сообщается в результатах OLS. Поэтому нет смысла их сравнивать.
Интерпретация результатов модели пространственной ошибки
В модели пространственной ошибки коэффициенты регрессии можно интерпретировать аналогично стандартной линейной регрессии. Каждый коэффициент представляет изменение в зависимой переменной, вызванное единичным изменением в независимой переменной. Однако SEM также включает дополнительный компонент, Лаг невязки (лямбда), который играет ключевую роль в понимании пространственной зависимости в модели. Коэффициент Лага невязки (лямбда) всегда будет в диапазоне от -0.99 до 0.99.
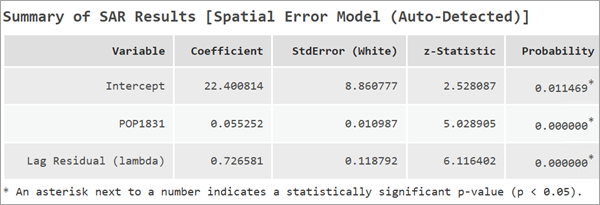
Положительные значения лямбда означают, что невязки испытывают кластеризацию, а отрицательные значения - что невязки испытывают пространственную дисперсию. Большие абсолютные значения (положительные или отрицательные) лямбда также означают, что существуют пространственные процессы, которые не были учтены независимыми переменными. Включение дополнительных релевантных независимых переменных может уменьшить коэффициент на более умеренные уровни.
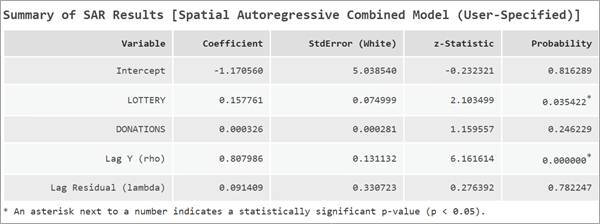
Интерпретация результатов пространственной комбинированной модели авторегрессии
Когда выбрана модель SAC, все разделы, применимые к SLM и SEM, отображаются в сообщениях.
Список литературы
Для внедрения этого инструмента были использованы следующие ресурсы:
- Anselin, L., and Sergio J. Rey. 2014. "Modern spatial econometrics in practice: A guide to GeoDa, GeoDaSpace and PySAL." ISBN 9780986342103.
Bivand, Roger and Gianfranco Piras. 2015. "Comparing implementations of estimation methods for spatial econometrics." Journal of Statistical Software. 63: 1-36. https://doi.org/10.18637/jss.v063.i18.
Kelejian, Harry H., and Ingmar R. Prucha. 2007. "HAC estimation in a spatial framework." Journal of Econometrics. 140, no. 1: 131-154. https://doi.org/10.1016/j.jeconom.2006.09.005.
Smith, Tony E. 2009. "Estimation bias in spatial models with strongly connected weight matrices." Geographical Analysis. 41, no. 3: 307-332. https://doi.org/10.1111/j.1538-4632.2009.00758.x.