Как работает инструмент Предполагаемое время до события

Инструмент Предполагаемое время до события предсказывает время до наступления события для набора наблюдений на основе времени, предшествующего событию, и определенных атрибутов наблюдений. Входные данные должны представлять собой смесь записей, в которых произошло событие, и записей, в которых это событие не произошло. Инструмент использует независимые переменные и оценивает, сокращают они или удлиняют время до события. Инструмент также предсказывает дополнительное время до наступления события для наблюдений, в которых это событие еще не произошло.

This video was created with ArcGIS Pro 3.5.

Каждое наблюдение во входных объектах или таблице должно иметь поля, содержащие возраст наблюдения, индикатор того, произошло ли уже это событие, и любые независимые переменные. Эти поля задаются в параметрах Поле Возраст, Поле Индикатор события и Независимые переменные, соответственно. Независимые переменные могут быть непрерывными или категориальными, а индикатор события должен принимать только значения 0 (событие не произошло) или 1 (событие произошло). Для поля Возраст это часто будет фактический возраст элемента, но в целом это промежуток времени, начинающийся с первого возможного времени, когда событие могло бы произойти, и заканчивающийся в момент, когда событие произошло (или текущее время, если событие не произошло). Например, чтобы оценить продолжительность жизни деревьев, значения поля Возраст должны соответствовать текущему возрасту дерева, если оно живо, или возрасту дерева, когда оно умерло. Однако для оценки времени до повторного ареста значения в поле должны соответствовать периоду времени с момента освобождения лица из-под стражи (когда может произойти первый повторный арест) до момента повторного ареста (или текущей даты, если лицо не подвергалось повторному аресту). Единицу измерения возраста (часы, дни, годы и т.д.) можно не указывать, но все результаты должны интерпретироваться в одинаковых единицах времени.

Инструмент создает множество выходных данных, числовых и графических, чтобы понять, как независимые переменные влияют на время до события, предсказать, когда событие произойдет, и оценить точность и надежность модели.

Возможное применение

Модели времени до события полезны в различных областях, где целью является оценка времени, которое требуется для его наступления, а также факторы, влияющие на его сроки. Ниже приведены некоторые потенциальные варианты применения этого инструмента:

• Техническое обслуживание инфраструктуры — оцените время, через которое произойдет протечка трубопровода, когда потребуется капитальный ремонт моста или выйдет из строя трансформатор. Независимые переменные могут включать тип материала (категориальная), воздействие экстремальных погодных условий (категориальная) и транспортную нагрузку (непрерывная).
• Управление лесным хозяйством — моделируйте время, когда дерево достигнет определенного диаметра, возникнет необходимость вырубки или оно погибнет от болезни. Независимые переменные могут включать начальный диаметр ствола (непрерывная), вид (категориальная), качество почвы (непрерывная) и конкуренцию со стороны близлежащих деревьев (категориальная).
• Дефолт по кредиту — прогнозирование времени до момента, когда заемщик не выполнит свои обязательства по кредиту. Независимые переменные могут включать сумму кредита (непрерывная), кредитный рейтинг (непрерывная), тип занятости (категориальная) и историю прошлых платежей (категориальная).
• Удержание клиентов — оценка того, когда клиент отменит подписку или сменит поставщика услуг. Независимые переменные могут включать сумму ежемесячного счета (непрерывная), продолжительность контракта (категориальная), количество жалоб на обслуживание клиентов (непрерывная) и полученные рекламные скидки (категориальная).
• Производство — прогнозируйте, когда оборудование потребует технического обслуживания или замены. Независимыми переменными могут быть часы работы (непрерывная), модель оборудования (категориальная) и температура на заводе (непрерывная).

Анализ времени до события и анализ выживаемости

Анализ времени до события - это раздел статистики, который оценивает, объясняет и предсказывает, когда для набора наблюдений произойдет событие, в котором предполагается, что каждое наблюдение столкнется с этим событием через некоторый промежуток времени. Анализ времени до события наиболее широко используется в медицинских исследованиях, в которых его обычно называют анализом выживаемости, поскольку моделируемым событием является смерть человека. По этой причине большая часть терминологии и концепций в анализе времени до события заимствована из анализа выживаемости. Например, промежуток времени до того, как наблюдение столкнется с событием, называется его продолжительностью жизни, а кривая, оценивающая время до события, называется кривой выживаемости. Для таких приложений, как прогнозирование гибели деревьев или сбоя в работе инфраструктуры, терминология подходит естественным образом, но она менее понятна, например, при оценке времени до повторного ареста. В этом случае время выживания будет равно промежутку времени до повторного ареста. Аналогичным образом, когда речь идет о вероятности того, что человек проведет по крайней мере пять лет без повторного ареста, это можно было бы сформулировать как вероятность того, что время его жизни превысит пять лет. В этой теме мы будем переходить от обсуждения времени до события к времени выживания в зависимости от контекста, но их следует представлять как одно и то же понятие.

Еще одно различие между анализом времени до события и анализом выживаемости заключается в том, что анализ выживаемости в первую очередь направлен на оценку влияния лечения (обычно препарата, проходящего медицинские испытания) на продолжительность жизни и в меньшей степени ориентирован на прогнозирование продолжительности жизни отдельных людей. По сути, вопрос заключается в том, увеличивает ли препарат продолжительность жизни, а не в том, как долго проживет тот или иной человек. Однако анализ времени до события в большей степени ориентирован на прогнозирование того, когда произойдет событие для отдельных наблюдений, и несколько менее ориентирован на оценку того, увеличивают или уменьшают время выживания независимые переменные. Хотя все модели анализа выживаемости могут быть использованы для анализа времени до события (и наоборот), некоторые модели подходят лучше, чем другие. В частности, этот инструмент использует параметрическую модель ускорения времени наступления отказа, которая больше подходит для прогнозирования времени до наступления события, в то время как в медицинских испытаниях обычно используется непараметрическая модель пропорциональных рисков Кокса, которая больше подходит для оценки эффективности медицинского лечения.

Кривые выживаемости

При оценке времени до события для каждого наблюдения создается кривая выживаемости, зависящая от их независимых переменных. Кривая выживаемости - это функция, которая отображает вероятность того, что время выживания превысит заданный промежуток времени (другими словами, вероятность того, что индивид все еще жив по истечении заданного времени). Кривая выживаемости всегда начинается с 1 и со временем уменьшается до 0. Например, следующая кривая выживания напоминает кривую выживания людей:

Согласно этой кривой, подавляющее большинство людей доживает до 20-летнего возраста, прежде чем эта доля начинает стремительно снижаться. К 60 годам чуть менее 80 процентов людей все еще будут живы. Среднее время выживания (0.5 по оси y) составляет приблизительно 80 лет, а к 100 годам особей почти не остается.

Исходя из кривой выживания, можно рассчитать любые квантили времени до события. Например, 5-^й процентиль времени до события - это значение по оси x, когда кривая равна 0.95 (когда существует 95-процентная вероятность того, что событие еще не произошло), а 75-^й процентиль - это когда кривая равна 0.25. Эти квантили можно использовать для создания доверительных интервалов; например, время между 5-^м и 95-^м процентилями является 90-процентным доверительным интервалом для времени до события. Хотя можно рассчитать любые квантили, кривые выживаемости часто суммируются по среднему времени выживания (значению оси x, когда кривая выживаемости равна 0,5).

Модель ускоренного времени отказа

Статистическая модель, используемая для оценки времени до наступления события, называется моделью ускоренного времени отказа (AFT). Модели AFT работают в предположении, что каждое наблюдение стареет с разной скоростью, в зависимости от их индивидуальных независимых переменных. Например, часто говорят (хотя это и неправда), что собаки стареют в семь раз быстрее людей, что 3-летняя собака находится на том же этапе своей жизни, что и 21-летний человек. В другом примере можно было бы предположить, что два моста деградируют с разной скоростью. Одному мосту может быть 30 лет, и он может считаться таким же изношенным, как и другой мост, которому всего 10 лет, в зависимости от характеристик мостов, таких как строительные материалы, интенсивность движения и условия окружающей среды.

В моделях AFT влияние независимых переменных заключается в ускорении или замедлении времени до наступления события, и выражается в виде отношения времени. Соотношение времени между двумя наблюдениями, A и B (каждое с разными независимыми переменными), представляет собой соотношение ожидаемой продолжительности жизни A и B. Например, соотношение времени, равное 1.3, означает, что продолжительность жизни наблюдения A, как ожидается, будет на 30 процентов дольше, чем B. Аналогично, соотношение времени, равное 0.6, означает ожидание, что она будет на 40 процентов короче. Соотношение времени, равное 1, означает, что оба наблюдения, как ожидается, будут иметь одинаковую продолжительность жизни. Обратите внимание, что соотношение времени подразумевает базовую линию или эталон, с которым проводится сравнение (в данном случае, продолжительность наблюдения B).

Эффект соотношения времени заключается в том, что кривая выживаемости растягивается по горизонтали. Например, на рисунке ниже показаны четыре кривые выживаемости, показывающие влияние соотношений времени, равных 1 (синяя кривая, с которой выполняется сравнение), 2 (оранжевая кривая), 3 (зеленая кривая) и 4 (красная кривая), слева направо. Трудно заметить, что кривые являются растянутыми версиями друг друга, поэтому средняя продолжительность жизни показана горизонтальной пунктирной линией. Обратите внимание, что среднее время выживания при соотношении времени 2 в два раза больше среднего времени при соотношении 1. Аналогично, медианное время выживания при соотношениях времени 3 и 4 в три и четыре раза превышает среднее время выживания при соотношении 1, соответственно. Хотя пунктирная линия расположена по медиане, использование любого другого значения оси y также сохранит эти соотношения.

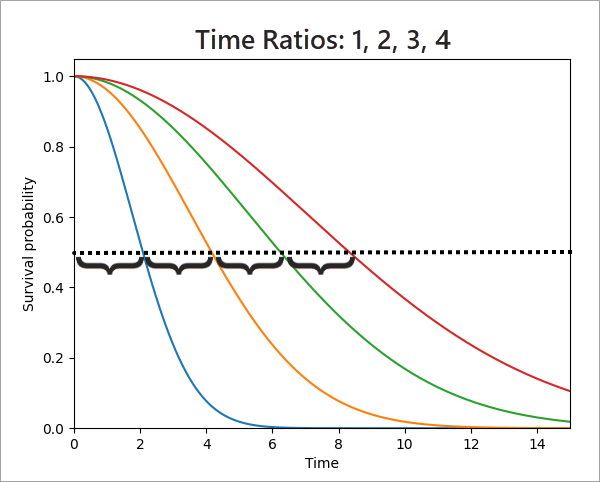
Использование самой левой синей кривой в качестве базовой линии было произвольным выбором. Если бы самая правая красная кривая была определена как базовая линия для сравнения, вместо синей, то соотношения времени были бы равны 0.25, 0.5, 0.75 и 1 (слева направо). Эти соотношения времени, меньшие 1, указывают на то, что красная кривая выживаемости имеет самую продолжительную ожидаемую выживаемость среди четырех кривых.

Инструмент оценит соотношение времени для каждой независимой переменной, проверит статистическую значимость соотношения времени и отобразит результат в сообщениях (дополнительную информацию см. в разделе Сообщения геообработки ниже). Интерпретация соотношения времени зависит от того, является ли независимая переменная категориальной или непрерывной, поскольку они по-разному задают свои базовые линии. Для категориальных переменных одна из категорий должна быть обозначена как эталонная категория, и для всех остальных категорий будут созданы соотношения времени по сравнению с эталонной категорией. Например, если поле категориальной переменной имеет уникальные значения A, B и C, а категория A является эталонной, соотношения времени будут рассчитаны только для категорий B и C. Если соотношение времени для категории B равно 2.2, это означает, что наблюдение в категории B, по оценкам, продлится в 2.2 раза дольше, чем наблюдение в категории A, при условии, что все остальные атрибуты равны (или, что эквивалентно, кривые выживаемости для категории B растянуты в 2.2 раза шире, чем кривые выживаемости для категории A). Инструмент использует первую категорию, отсортированную в алфавитно-цифровом порядке, в качестве эталонной, но вы можете переклассифицировать значения полей, чтобы выбрать, какая категория будет использоваться в качестве эталонной.

Для непрерывных переменных соотношение времени - это изменение продолжительности жизни при увеличении независимой переменной на одну единицу. В этом случае проводится сравнение между двумя наблюдениями, которые отличаются по значению независимой переменной ровно на 1 (при равенстве всех остальных независимых переменных). Например, при оценке продолжительности жизни дерева, если диаметр ствола в метрах является независимой переменной, соотношение времени измеряет увеличение (или уменьшение) продолжительности жизни путем увеличения диаметра дерева на 1 метр. Если деревья с большим диаметром ствола, как правило, живут дольше, соотношение времени будет больше 1, а если они, как правило, живут короче, соотношение будет меньше 1. Поскольку соотношение времени является множителем, увеличение независимой переменной на две единицы увеличит продолжительность жизни на соотношение времени в квадрате; увеличение независимой переменной на три единицы увеличит продолжительность жизни на соотношение времени в кубе; и так далее. Такой сложный характер отношения времени для непрерывных независимых переменных может вызвать трудности при моделировании (дополнительную информацию и рекомендации смотрите в разделе Рекомендации по применению, ограничения и рекомендуемый рабочий процесс ниже).

Оценка модели AFT

Модель AFT использует распределение Вейбулла для моделирования кривой выживаемости:

Параметр масштаба (λ) оценивается как линейная модель независимых переменных (X_i) и оценочных коэффициентов (β_i). Именно параметр масштаба определяет степень растяжения кривой выживаемости, как описано в предыдущем разделе. Интуитивно понятно, что определенные атрибуты наблюдения будут растягивать (или сжимать) кривую выживаемости для этого наблюдения, в зависимости от того, связаны ли его атрибуты в целом с большей или меньшей продолжительностью жизни.

Параметр формы (ρ) является общим для всех наблюдений и позволяет кривой выживаемости принимать различные формы в пределах одного и того же временного интервала. На следующем рисунке показаны различные формы распределений Вейбулла с одним и тем же параметром масштаба:

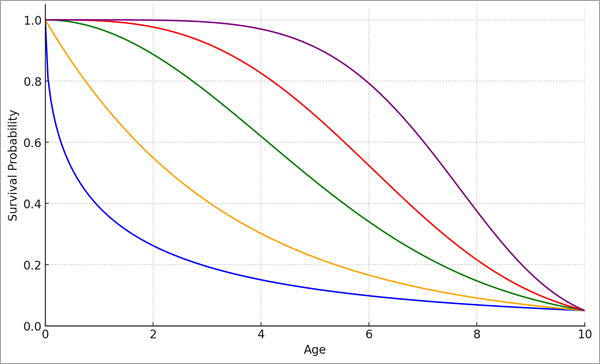
Параметр формы иногда называют параметром ускорения, поскольку он определяет, ускоряется или замедляется кривая выживаемости. Ускорение измеряется с помощью функции риска, которая определяется как вероятность того, что событие произойдет в определенный момент времени, при условии, что событие не произошло до этого времени. Например, если более старые мосты с большей вероятностью будут нуждаться в ремонте в ближайшем будущем, чем более новые, то функция риска со временем возрастает (другими словами, более старые мосты подвержены большей опасности, чем более новые), поэтому кривая выживаемости со временем ускоряется. И наоборот, если более старые мосты с меньшей вероятностью будут нуждаться в ремонте в ближайшем будущем, чем более новые, уровень опасности снижается, а кривая выживаемости замедляется. Значения параметра формы, превышающие 1, указывают на ускоряющуюся кривую выживаемости, а значения, меньшие 1, указывают на замедляющуюся кривую. Однако модель не может оценить различные уровни риска, при которых кривая выживаемости как ускоряется, так и замедляется в разное время (например, продолжительность жизни человека выше для младенцев, затем ниже для детей и молодых людей, затем снова выше для пожилых людей).

Все коэффициенты и параметр формы оцениваются с использованием метода максимального подобия и отображаются инструментом в виде сообщений.

Закрытые наблюдения и предсказания

В предыдущих разделах описывалось, как рассчитываются кривые выживаемости для каждого наблюдения, независимо от того, произошло ли событие для данного наблюдения ранее или нет. Например, кривая выживаемости может быть создана для моста, который уже вышел из строя. По сути, эта кривая выживаемости показывает ожидаемый срок службы моста, если бы он был построен с теми же характеристиками сегодня. Хотя эта информация может быть полезной, гораздо полезнее создать кривые выживаемости, предсказывающие дополнительную продолжительность жизни наблюдений, в течение которых событие не произошло (например, предсказать, как долго прослужит существующий мост, пока ему не потребуется ремонт).

Наблюдения, в которых событие еще не произошло, называются закрытыми наблюдениями, а наблюдения, в которых событие произошло, называются открытыми наблюдениями. Эта терминология исходит из того факта, что не закрытые наблюдения, содержат полную информацию (известно время их выживания), а закрытые наблюдения, содержат только частичную информацию: точное время выживания неизвестно, но известно, что оно превышает некоторый промежуток времени (текущий возраст наблюдения). Это сопоставимо с идеей о том, что документ может быть открытым или закрытым: вся информация документа может быть доступна (открытый документ) или ее части могут быть отредактированы цензором (закрытый документ).

Для закрытых наблюдений цель состоит в том, чтобы создать кривую выживаемости, которая оценивает дополнительное время до события, учитывая его текущий возраст. Эта дополнительная кривая продолжительности жизни может быть построена путем определения количества времени, которое индивид уже прожил. Математически, дополнительная кривая продолжительности жизни S_Add(T) вычисляется как S_Add(T) = S(C+T)/S(C) для дополнительных единиц времени T после времени закрытия C.

Дополнительную кривую времени выживания можно визуализировать как изменение масштаба кривой выживаемости наблюдений по истечении времени закрытия. Например, на рисунке ниже показана кривая выживаемости для наблюдения, которое было закрыто в момент времени 4. Исходя из его независимых переменных, существовала приблизительно 60-процентная вероятность того, что индивид проживет по крайней мере четыре единицы времени (значение по оси y на момент закрытия). Однако поскольку известно, что индивид пережил по крайней мере четыре единицы времени (время закрытия), значения по оси y снова масштабируются и начинаются с 1 (другими словами, существует 100-процентная вероятность того, что индивид пережил по крайней мере четыре единицы времени). Аналогично, ось x снова начинается с 0, чтобы измерить время, начиная с момента закрытия. В этом примере среднее время выживания индивидуума с учетом этих независимых переменных составляет приблизительно пять единиц времени (где кривая пересекает 0.5 по исходной оси y), но если известно, что индивидуум уже пережил четыре единицы времени, среднее дополнительное время выживания составляет приблизительно две единицы (где кривая пересекает 0.5 по оси y в меньшем масштабе) при общей продолжительности жизни в шесть единиц времени. Другими словами, знание того, что индивид уже прожил четыре единицы времени, увеличивает общую среднюю продолжительность жизни примерно с пяти единиц до шести единиц времени. Чем дольше сохраняется наблюдение до того, как оно будет закрыто, тем дольше оно, как ожидается, будет выживать по сравнению с его базовой кривой выживаемости.

Для закрытых наблюдений, кривые выживаемости, показывающие дополнительное время до события после закрытия, отображаются во всплывающих диаграммах выходных характеристик или в таблице. Как для закрытых, так и для не закрытых объектов индивидуальные кривые выживаемости также отображаются во всплывающих диаграммах.

Возраст наблюдения на момент закрытия обычно соответствует текущему возрасту наблюдения, но это также может быть возраст, в котором объект наблюдался в последний раз, например, дата самого последнего осмотра моста. В этом случае дополнительное время выживания начинается с возраста наблюдения, когда оно наблюдалось в последний раз.

Кривая Каплана-Мейера

Поскольку каждая комбинация независимых переменных приводит к различной кривой выживаемости, может быть трудно количественно определить, ожидается ли, что у конкретного наблюдения продолжительность жизни будет больше или меньше, чем у обычного наблюдения. Некоторые из независимых переменных наблюдения увеличивают продолжительность жизни, а другие сокращают ее, но неясно, увеличивают ли они в целом продолжительность жизни наблюдения или сокращают ее. Чтобы получить кривую, которую можно использовать в качестве основы для сравнения с индивидуальными кривыми выживаемости, инструмент вычисляет кривую Каплана-Мейера для полученных данных.

Кривая Каплана-Мейера - это непараметрическая оценка функции выживаемости, которая игнорирует независимые переменные и оценивает долю наблюдений, которые не сталкивались с данным событием с течением времени. Это делается это путем последовательной корректировки времени события и времени закрытия, используя следующее уравнение:

В этом уравнении E_i - это количество событий, произошедших в момент времени t_i, а N_i - количество наблюдений, которые не испытывали этого события или были закрыты до момента времени t_i.

Кривая визуализируется в виде ступенчатой функции, которая уменьшается с каждым разом, когда происходит событие. Кривая не может выходить за пределы времени наибольшего значения поля возраста, и вероятность выживания никогда не опустится ниже процента закрытых объектов. Например, на приведенной ниже кривой Каплана-Мейера наибольшее значение поля возраста составило приблизительно 3500 (максимальное значение по оси x), и чуть более 40 процентов наблюдений были закрыты (наименьшее значение кривой немного превышает 0.4).

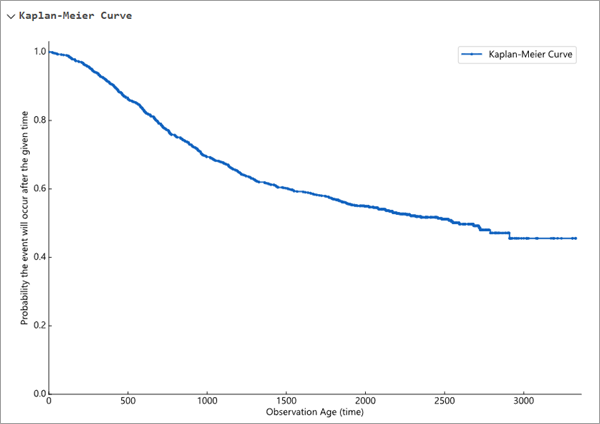
Кривая Каплана-Мейера для данных отображается в свертываемом разделе сообщений геообработки. Она также отображается во всплывающих диаграммах выходных объектов или таблиц, чтобы ее можно было напрямую сравнить с кривыми выживаемости отдельных наблюдений (более подробную информацию см. в следующем разделе).

Выходные данные инструмента

Инструмент возвращает различные выходные данные для анализа результатов. Выходные данные включают в себя выходной класс объектов или таблицу, сообщения геообработки, всплывающие диаграммы и гистограмму.

Выходные объекты или таблица

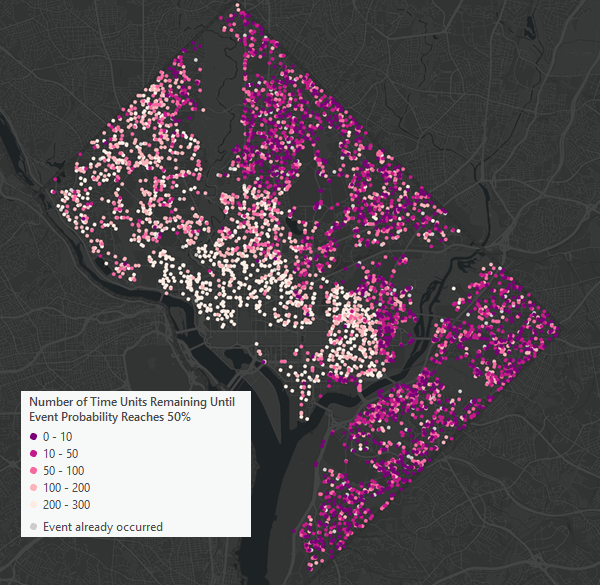
Для ввода объектов выходной слой объектов будет отображаться на основе медианного дополнительного времени до события. Закрытые объекты выделены красным и розовым оттенками, причем более глубокие оттенки указывают на то, что событие, по прогнозам, произойдет раньше. Не закрытые объекты отображаются светло-серым цветом и настраиваются так, чтобы они отображались под закрытыми объектами, если их символы перекрываются.

Как для табличных входных данных, так и для входных данных объектов выходные данные будут содержать копии всех входных полей, а также различные квантили дополнительного времени до события. Поля будут содержать 5-^й, 10-^й, 25-^й, медианный (50-^й), 75-^й, 90-^й и 95-^й процентили дополнительного времени к событию. Вы можете использовать эти значения для создания диапазонов вероятности наступления события, например, используя 5-^й и 95-^й процентили для построения 90-процентного доверительного интервала. Для не закрытых объектов все значения поля квантиля будут равны нулю, поскольку предсказывать, когда произойдет событие, нет необходимости, если событие уже произошло.

Всплывающие диаграммы

Если включен параметр Включить всплывающие окна кривой выживания, выходные объекты или таблица также будут содержать поле всплывающих диаграмм для каждого наблюдения. Для объектов можно получить доступ к всплывающим диаграммам, щелкнув по объекту на карте с помощью инструмента Исследовать. Для таблиц можно получить доступ к всплывающим диаграммам, щелкнув правой кнопкой мыши строку записи в таблице атрибутов.

Для не закрытых наблюдений на всплывающей диаграмме будет отображаться кривая выживаемости объекта (синяя кривая) и синяя точка, указывающая время события. Это позволяет увидеть, произошло ли событие в наблюдении в начале или в конце его прогнозируемой продолжительности жизни. Наблюдения с событиями, произошедшими намного раньше или позже, чем ожидалось в соответствии с моделью, могут потребовать дальнейшего изучения. Кривая Каплана-Мейера (оранжевая кривая) также включена во всплывающую диаграмму в качестве основы для сравнения. Это позволяет вам увидеть, ожидается ли, что это наблюдение продлится дольше или короче, чем обычное наблюдение. Например, на изображении ниже кривая выживаемости расположена ниже и левее кривой Каплана-Мейера, что означает, что событие должно было произойти раньше, чем в большинстве других наблюдений. Синяя точка также находится в середине кривой выживаемости, что означает, что событие произошло приблизительно в то время, когда предсказывала модель, на основе ее независимых переменных.

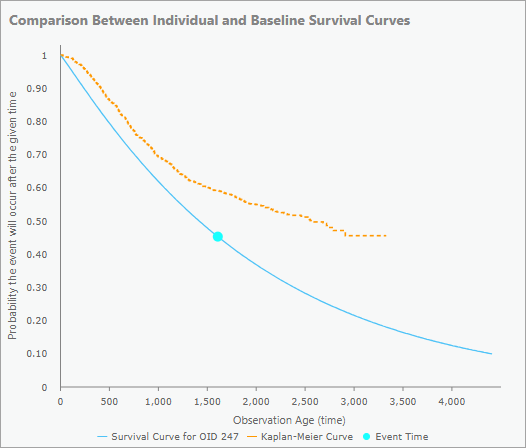
Примечание:

Ось x всплывающих диаграмм будет продлеваться до тех пор, пока кривая выживаемости не достигнет 0.1 (пороговое значение необходимо, поскольку кривые выживаемости никогда не достигают нуля). Однако, поскольку кривая Каплана-Мейера не может превышать наибольшее значение поля возраста, она часто заканчивается до того, как кривая выживаемости достигнет 0.1. Чтобы обеспечить видимость кривой Каплана-Майера, ось x никогда не будет длиннее кривой Каплана-Мейера более чем в два раза, даже если кривая выживаемости все еще не достигнет 0.1.

Для закрытых объектов всплывающие диаграммы также будут содержать кривую выживаемости и кривую Каплана-Мейера для наблюдения, но время закрытия будет обозначено синим кружком, а не точкой.

Только для закрытых объектов всплывающие диаграммы также будут содержать график дополнительного времени к событию после закрытия. Среднее дополнительное время отображается в виде пунктирных горизонтальных и вертикальных линий, чтобы определить время, когда модель предсказывает 50-процентную вероятность того, что событие произойдет. Ось x будет продлеваться до тех пор, пока кривая не достигнет 0.4, чтобы гарантировать постоянное отображение медианы.

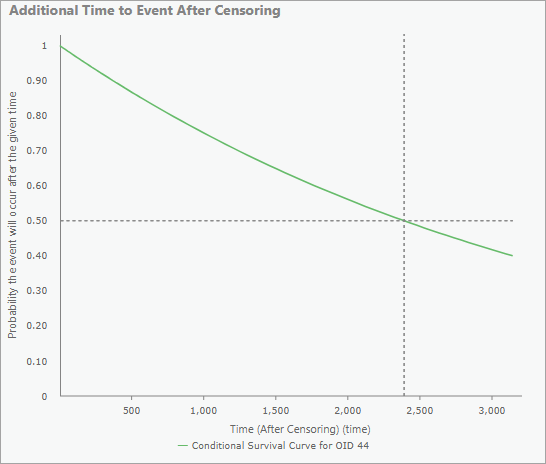
Вы можете навести курсор на любую из всплывающих диаграмм, чтобы увидеть точные значения кривых.

Сообщения геообработки

Сообщения о геообработке содержат различные разделы, в которых кратко описываются эффекты независимых переменных и диагностика, связанная с тем, насколько хорошо модель соответствует данным.

Непрерывные независимые переменные

В первом разделе сообщений содержится таблица, обобщающая влияние непрерывных независимых переменных. Для каждой переменной в таблице отображаются соотношение времени, коэффициент и его стандартная ошибка (по параметру шкалы распределения Вейбулла), z-оценка и p-значение, проверяющие статистическую значимость коэффициента, а также нижняя и верхняя границы для 95-процентного доверительного интервала соотношения времени.

В конце приводится строка для интерсепта (отрезка), но необработанные значения обычно не имеют осмысленной интерпретации. Вместо этого цель отрезка состоит в том, чтобы привести кривые выживаемости к единице времени поля возраста. Например, если бы вы преобразовали значения поля возраста из часов в дни, все временные соотношения остались бы прежними, но временное соотношение отрезка было бы разделено на 24 (преобразование из часов в дни). Вот почему единицу измерения для поля возраста задавать не нужно, инструмент будет давать эквивалентные результаты независимо от единицы измерения.

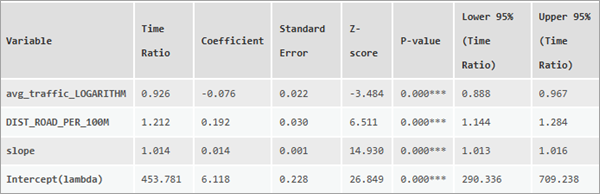
Примечание:

Для каждой переменной коэффициент и его стандартная ошибка непосредственно оцениваются моделью AFT и проверяются на статистическую значимость с помощью z-критерия. Затем из этого коэффициента вычисляется отношение времени по экспоненте: exp(coefficent). Временные соотношения обычно предпочтительнее коэффициентов, поскольку временные соотношения интерпретируются относительно исходного времени выживания, тогда как коэффициенты интерпретируются относительно логарифма времени выживания. Верхняя и нижняя границы доверительного интервала рассчитываются путем создания доверительного интервала для коэффициента и вычисления экспоненциальной зависимости конечных точек.

Категорийные независимые переменные

Во втором разделе сообщений содержится таблица, обобщающая влияние категорийных независимых переменных. Для каждой категориальной переменной отображается таблица, показывающая влияние каждой из ее категорий. Базовая категория отображается над таблицей, а все временные соотношения должны интерпретироваться относительно этой категории. Например, на рисунке ниже категориальная переменная - это номер отделения, а отделения 1 - это контрольная категория. Наблюдения в отделении 2 длятся в 5.345 раза дольше, чем наблюдения в отделении 1 (соотношение времени равно 5.345), но наблюдения в отделении 8 длятся на 23.6% меньше, чем наблюдения в отделении 1 (соотношение времени равно 0.764). p-значения также показывают, что отделения 4, 5 и 7 существенно не отличаются от отделения 1.

Примечание:

Каждая категориальная переменная преобразуется в последовательность двоичных переменных (0 или 1), и эти двоичные переменные используются в качестве непрерывных независимых переменных в модели AFT. Для K категорий создается (K-1) двоичных переменных, и каждая категория получает двоичную переменную, за исключением эталонной категории (этот процесс называется кодированием индикатора). Одна категория должна быть исключена и использоваться в качестве эталонной, поскольку включение двоичных переменных для всех категорий приводит к идеальной коллинеарности, в результате чего модель не может оценить коэффициенты и временные соотношения.

Параметр формы Вейбулла

После таблиц коэффициентов независимых переменных в сообщениях отображается таблица, обобщающая параметры формы распределения Вейбулла. В таблице также приведены z-оценки и p-значения, позволяющие определить, отличается ли статистически параметр формы от 1. Также приведены нижняя и верхняя границы для 95-процентного доверительного интервала.

Параметр формы характеризует, ускоряется или замедляется кривая выживаемости. Значения, значительно превышающие 1, указывают на ускорение, а это означает, что чем старше наблюдение, тем больше вероятность того, что событие произойдет в ближайшем будущем. Значения, значительно меньшие 1, указывают на замедление, а это означает, что более новые наблюдения с большей вероятностью столкнутся с этим событием в ближайшем будущем. Значения, незначительно отличающиеся от 1, указывают на то, что новые и старые наблюдатели с одинаковой вероятностью столкнутся с этим событием в ближайшем будущем. Модель предполагает, что кривая выживаемости постоянно ускоряется или замедляется, но не может переключаться между ускорением или замедлением.

Суммарная статистика модели

Заключительный раздел сообщений представляет собой раздел Краткая информация модели, содержащий статистические данные, относящиеся к общей точности прогнозов и соответствию модели. В разделе отображается следующая статистика:

• Индекс соответствия — значение от 0 до 1, указывающее на вероятность того, что модель сможет правильно предсказать, будет ли продолжительность жизни одного объекта больше, чем другого. Значения, близкие к 1, указывают на то, что модель почти всегда может предсказать, какой из объектов столкнется с событием первым, а значения, близкие к 0.5, указывают на то, что модель предсказывает последовательность событий не лучше, чем случайно. Значения ниже 0.5 наблюдаются редко, но это означало бы, что модель менее точна, чем случайная вероятность. Это значение рассчитывается как доля парных индивидуумов, у которых модель правильно предсказала, кто из двух индивидуумов пережил событие первым. Закрытые объекты не используются в расчетах, поскольку время их выживания неизвестно. На практике это значение обычно составляет от 0.6 до 0.8.
• AIC — информационный критерий Акаике (AIC) для определения соответствия модели AFT. Это значение в основном носит информационный характер, но может использоваться в расширенных рабочих процессах, например, для построения вложенных тестов отношения правдоподобия между различными комбинациями независимых переменных.
• P-значение — p-значение для глобального теста значимости независимых переменных. Это значение показывает, значительно ли улучшает предсказания модели сопокупность независимых переменных. Если это значение не является статистически значимым (обычно оно превышает 0.05), то модель работает ненамного лучше, чем при полном отсутствии независимых переменных. Это значение определяется с помощью теста отношения правдоподобия.

Гистограмма остаточных отклонений

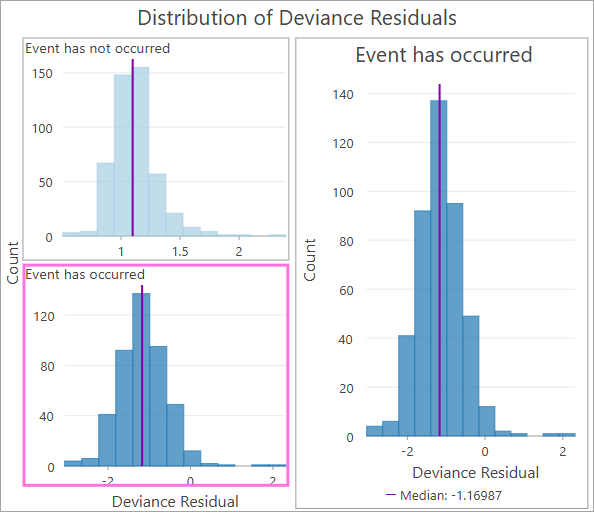
Выходной векторный слой также содержит гистограмму остаточных отклонений в наблюдениях. Остаточные отклонения концептуально аналогичны остаточным значениям в других регрессионных моделях в том смысле, что они количественно определяют, имело ли наблюдение более длительное или более короткое время жизни, чем было предсказано моделью. Положительные остаточные отклонения означают, что индивид прожил дольше, чем было предсказано, а отрицательные - что у индивида была более короткая продолжительность жизни (обратите внимание, что некоторые источники определяют знак, положительный или отрицательный, противоположным образом). Если модель хорошо соответствует, среднее значение остаточных отклонений должно быть близко к нулю.

Для не закрытых наблюдений некоторые из них будут иметь более длительную или более короткую продолжительность жизни, чем предсказывает модель, поэтому их остаточные отклонения могут быть как положительными, так и отрицательными. Однако остаточные отклонения для закрытых наблюдений всегда будут положительными. Поэтому гистограмма разделена полем индикатора события, показывая отдельные гистограммы для закрытых и не закрытых наблюдений.

Остаточные отклонения наиболее полезны для изучения выбросов в результатах, а экстремальные значения на обеих гистограммах указывают на разные вещи. Для не закрытых наблюдений экстремальные отрицательные значения указывают на то, что наблюдение пережило событие намного раньше, чем было предсказано моделью, а экстремальные положительные значения указывают на то, что оно пережило событие намного позже. Значения, превышающие три в любом направлении, вероятно, указывают на выбросы или аномальные наблюдения, которые могут потребовать дальнейшего изучения или удаления из набора данных. Для закрытых наблюдений эти значения менее значимы, но они обычно измеряют, насколько далеко продвинулось наблюдение в течение продолжительности жизни до того, как оно было закрыто. Значения в самой левой части (близкие к нулю) указывают на то, что наблюдение было закрыто на очень раннем этапе своего существования, а значения в крайнем правом углу указывают на то, что оно было закрыто очень поздно (возможно, оно уже прожило дольше, чем предсказывает модель, даже до того, как оно было закрыто).

Остаточные отклонения рассчитываются по следующему формуле:

В это уравнении S-hat_i(t_i) - это расчетная вероятность выживания наблюдения на момент события (или на момент, когда оно было закрыто), а δ_i - индикатор события.

Примечание:

Остаточные отклонения для закрытых наблюдений всегда положительны, потому что, если индивид уже прожил какое-то время, прогнозируется, что его общая продолжительность жизни будет больше, чем предсказывает его базовая кривая выживаемости (смотрите изображение в разделе Закрытые наблюдения и предсказания выше, чтобы понять, почему это так). Процесс гарантирует, что общее среднее остаточных отклонений (с учетом закрытия и без него) для правильно настроенных моделей равно нулю.

Рекомендации по применению, ограничения и рекомендуемый рабочий процесс

Этот инструмент обладает рядом ограничений, также в нем имеются некоторые особенности. Ниже приведены общие рекомендации по использованию этого инструмента:

• Предсказать, когда произойдет то или иное событие, крайне сложно, поэтому мы рекомендуем вам придерживаться реалистичных ожиданий. Этот инструмент может извлекать информацию только из предоставленных вами независимых переменных, но такие сложные явления, как устаревание инфраструктуры, связаны с многочисленными факторами, которые часто носят локальный характер и специфичны для каждого объекта. На практике следует рассматривать прогнозируемое время до события как общие указания на то, когда оно может произойти, а не как точные прогнозы относительно конкретных дат. Также следует проявлять осторожность и определенный скептицизм при экстраполяции на время, превышающее время наибольшего события во входных данных. Несмотря на то, что результаты анализа времени до события часто бывают неточными, они все же могут быть очень полезны для получения общих оценок будущих затрат или для определения приоритетов и распределения ресурсов для наблюдений, которые, скорее всего, произойдут.

• Модели времени до события по своей сути не являются пространственными, но включение пространственной информации может улучшить модель за счет учета географических закономерностей. Рассмотрите возможность добавления пространственных независимых переменных, таких как географические регионы, в качестве категорийных независимых переменных или расстояния до ключевых объектов в качестве непрерывных независимых переменных. Например, при моделировании гибели деревьев в городах расстояние до ближайшего здания может быть важным из-за уменьшения количества солнечного света в тени зданий.

• Модель предполагает, что событие будет происходить для каждого наблюдения через некоторое время, но в некоторых случаях это не так. Например, при прогнозировании времени до повторного ареста понятно, что некоторые люди никогда не будут повторно арестованы, но модель все равно предскажет для них кривую выживаемости. На практике, если прогнозируемое дополнительное время выживания для наблюдения очень велико, это может означать, что событие, скорее всего, никогда не произойдет.
• Для непрерывных независимых переменных временные соотношения представляют собой мультипликативное изменение кривой выживаемости при увеличении независимой переменной на одну единицу. Однако для некоторых переменных изменение на одну единицу является незначительным и приводит к временным соотношениям, очень близким к 1, даже для очень значимых и важных независимых переменных. Например, при прогнозировании ремонта кровли, в качестве независимой переменной можно использовать размер здания в квадратных метрах. Однако, даже если размер здания очень важен, увеличение всего на один квадратный метр окажет лишь незначительное влияние на кривую выживаемости. Если одна из ваших независимых переменных очень значима (высокая z-оценка и низкое p-значение), но полученное соотношение времени равно 1.000 или очень близок к нему, рассмотрите возможность деления значений поля на большую константу. Например, деление переменной квадратных метров на 100 приведет к получению идентичных кривых выживаемости и результатов значимости, но соотношение времени теперь будет интерпретироваться как изменение размера здания на 100 квадратных метров, что может привести к более понятному соотношению времени. Умножение или деление любой из независимых переменных (или поля возраста) на постоянное значение приведет к получению эквивалентных кривых выживаемости, поэтому рекомендуется изменить масштаб значений, если это поможет в интерпретации результатов.
• Поскольку соотношение времени является мультипликативным, большие значения (по сравнению со значениями остальных данных) любой непрерывной независимой переменной могут привести к нестабильности и неоправданно длинным или коротким кривым выживаемости. Временное соотношение представляет собой изменение при увеличении независимой переменной на одну единицу, и оно увеличивается экспоненциально. Например, увеличение независимой переменной на пять единиц увеличивает кривую выживаемости по отношению времени в пятой степени. При больших значениях независимой переменной эти показатели могут стать очень большими и привести к нестабильным кривым выживаемости. Выбросы будут особенно проблематичными, но даже большие значения, которые не являются выбросами, все равно могут привести к нестабильным кривым выживаемости. В этих случаях потенциальным решением является применение логарифмического преобразования к независимой переменной. Это затруднит интерпретацию временного отношения для независимой переменной (теперь это растяжение кривой выживаемости при увеличении логарифма независимой переменной на одну единицу), но преобразование независимой переменной в логарифмическую шкалу часто нейтрализует эффект усугубления временного соотношения и дает более разумные кривые выживаемости.

• Хотя для оценки параметров модели используются как закрытые, так и не закрытые наблюдения, не закрытые наблюдения предоставляют наибольшую информацию, поскольку известно их точное время жизни. В целом рекомендуется использовать не менее 10 не закрытых наблюдений для каждой независимой переменной. Однако категориальные переменные следует рассматривать как множественные переменные. Категориальная переменная с двумя категориями считается одной, три категории считаются двумя переменными, четыре категории считаются тремя переменными и т.д. Кроме того, каждая категория должна содержать несколько не закрытых наблюдений, чтобы наилучшим образом оценить влияние всех категорий категориальной переменной.

• В некоторых случаях может быть трудно определить начальную точку времени жизни наблюдения. Например, мосты подвергаются периодическому ремонту и техническому обслуживанию, поэтому при прогнозировании времени следующего ремонта датой начала может быть дата первоначального строительства моста или дата, когда мост в последний раз нуждался в ремонте. В этом случае вам нужно будет решить, считается ли отремонтированный мост эквивалентным новому мосту. Если вы решите, что отремонтированные мосты эквивалентны новым, один и тот же мост может быть включен в данные несколько раз, чтобы облегчить построение модели (по одному разу для каждого случая, когда требовался ремонт). Однако, если вы решите, что отремонтированный мост не эквивалентен новому, вы можете попробовать использовать количество предыдущих случаев, когда мост требовал ремонта, в качестве независимой переменной.

Хотя идеального рабочего процесса для анализа времени до события не существует, ниже приведен общий шаблон для построения и оценки модели:

1. Изучите входные данные и решите, какие независимые переменные вы будете использовать. Выберите независимые переменные, которые, как вы знаете или предполагаете, связаны со временем выживания, и изучите их с помощью диаграмм. Диаграммы независимых переменных относительно времени выживания будут особенно полезны для определения того, какие переменные связаны со временем выживания (к сожалению, для этого можно использовать только не закрытые наблюдения). Обратите особое внимание на любые отклонения в непрерывных независимых переменных и рассмотрите возможность их устранения или применения логарифмического преобразования. Что касается категориальных переменных, убедитесь, что для каждой категории имеется несколько не закрытых наблюдений, и, возможно, объедините или удалите любые категории с небольшим количеством не закрытых наблюдений.
2. В зависимости от того, как представлены данные, для создания полей индикатора возраста и события может потребоваться значительный объем работы с данными. Например, вам может потребоваться преобразовать поля даты начала и окончания в значения возраста (для этого будет полезно использовать выражение DateDiff Arcade в инструменте Вычислить поле) или преобразовать текстовое поле в двоичное поле индикатора события.
3. После запуска инструмента и просмотра любых предупреждений или ошибок вам следует проверить общую точность модели и найти признаки неправильной или неточной настройки модели. Просмотрите гистограмму остаточных отклонений и обратите особое внимание на экстремальные остаточные значения (положительные или отрицательные) в не закрытых наблюдениях. Оцените p-значение и индекс соответствия в разделе сообщений в Краткой информации модели, и если p не является значимым (что случается редко), вам следует попытаться найти независимые переменные, которые лучше оценивают время выживания. Вам также следует оценить, является ли индекс соответствия приемлемо высоким, сохраняя реалистичные ожидания.
4. Если общая модель достаточно точна, вам следует затем просмотреть таблицы коэффициентов в сообщениях, чтобы узнать, какие независимые переменные повлияли на продолжительность жизни и определить степень их влияния. Рассмотрите возможность удаления любых независимых переменных, которые не являются статистически значимыми.
5. Что касается объектов, изучите выходной слой объектов на карте и найдите пространственные закономерности. Имеется ли в некоторых областях более длительное время выживания, чем в других?
6. Наконец, изучите всплывающие диаграммы и таблицу атрибутов отдельных интересующих вас наблюдений, чтобы увидеть их расчетные кривые выживаемости.

Список литературы

Для внедрения этого инструмента были использованы следующие ресурсы:

• Collett, David. 2023. "Modelling survival data in medical research." Chapman and Hall/CRC. https://doi.org/10.1201/9781003282525.
• Davidson-Pilon, Cameron. 2019. "lifelines: survival analysis in Python." Journal of Open Source Software. 4(40), 1317, https://doi.org/10.21105/joss.01317.
• Klein, John P. and Melvin L. Moeschberger. 2003. "Survival Analysis: Techniques for Censored and Truncated Data." Springer Science & Business Media. ISBN 0-387-95399-X.