Как работает Мультимасштабное отклонение поверхности

Инструмент Мультимасштабное отклонение поверхности вычисляет максимальное отклонение поверхности в диапазоне пространственных масштабов (размер окрестностей различается). Выходные данные этого инструмента определяют это отклонение для ячейки и масштаб, при котором он был найден.

Выходные данные можно использовать для интерпретации объектов на входном растре поверхности и связанных с ним масштабов. На изображении ниже показаны результаты двух различных масштабов для одной и той же входной поверхности. Одни выходные данные используют масштаб 9 на 9 ячеек, а другие – 29 на 29 ячеек. Здесь меньший масштаб более чувствителен к локальным изменениям ландшафта и отражает более мелкие объекты поверхности. С другой стороны, больший масштаб показывает меньше подробностей, получая только крупные объекты поверхности.

Показано выходное отклонения в одинаковом экстенте для двух разных масштабов, в меньшем (второй рисунок) и большем (третий рисунок).

Как вычисляется значение максимального отклонения

Следующие шаги дают общее представление о внутренних процессах, используемых инструментом:

1. Масштабы для анализа задаются при помощи параметров Минимальное расстояние окрестности, Максимальное расстояние окрестности, Базовое приращение расстояния и Коэффициент нелинейности. Единицы измерения этих параметров управляются параметром Единицы расстояния.
2. Для каждой ячейки отклонение вычисляется при каждом найденном масштабе.
3. Вычисленные отклонения сравниваются в разных масштабах и наибольшие значения отклонений возвращаются.

Каждый из этих шагов более подробно описан в разделах ниже.

Как определяются масштабы для анализа

Масштабы для анализа определяются при помощи дополнительных параметров инструмента Мультимасштабный процентиль поверхности. Параметры Минимальное расстояние окрестности и Максимальное расстояние окрестности определяют минимальный и максимальный масштабы для анализа. Параметры Базовое приращение расстояния и Коэффициент нелинейности управляют увеличением расстояния окрестности между минимумом и максимумом.

Каждый масштаб представлен в виде значения расстояния окрестности. Анализ выполняется для нескольких расстояний окрестности в зависимости от настроек входных параметров.

Для заданной целевой ячейки расстояние окрестности измеряется от центра целевой ячейки во вне, создавая квадрат ячеек вокруг нее. Например, при расстоянии окрестности, равном 30 метрам, для растра поверхности с размером ячейки 10 метров получится окрестность 7 на 7 ячеей, как показано на рисунке ниже. Это значение, равное 30 метрам, было бы одним из масштабов, для которого рассчитывается максимальное отклонение.

Соотношение между расстоянием окрестности (оранжевая линия) и числом ячеек скользящего окна. Для размера ячеек 10 метров; при расстоянии окрестности 10 метров будет использоваться окно 3 на 3 ячейки (по умолчанию), при расстоянии окрестности 20 метров - окно 5 на 5 ячеек, при 30 метрах - 7 на 7 ячеек.

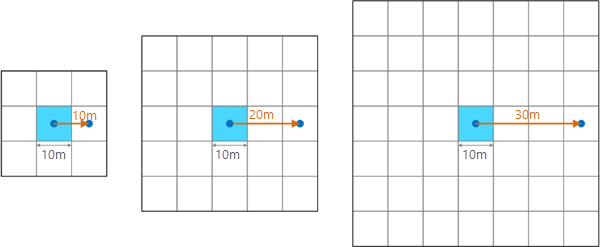
Минимально допустимое расстояние окрестности равно размеру ячейки входного растра. Это значение 1 ячейки, оно создает окрестность размером 3 на 3 ячейки. В приведенном выше примере этим минимумом является расстояние окрестности в 5 метров.

Расстояние окрестности не может быть больше, чем входной растр поверхности.

Если указанное расстояние окрестности не достигает диапазона, кратного размеру ячейки, оно округляется до следующего интервала, кратного размеру ячейки. Например, на рисунке выше указано значение окрестности 25 метров, которое округляется до следующего значения, кратного размеру ячейки, 30 метров.

Вычисления начинаются со значения параметра Минимальное расстояние окрестности, затем вычисляется каждое последующее расстояние окрестности.

Выражение для вычисления последующих расстояний окрестности выглядит следующим образом:

ni = no + [Δn × (i - no)]p

• Где:

  n_i = расстояние окрестности для шага i

  n_o = минимальное расстояние окрестности

  Δn = базовое приращение расстояния

  i = шаг, для которого вычисляется расстояние окрестности (где первый шаг имеет значение 1 + n_o)

  p = коэффициент нелинейности

Каждое новое идентифицированное расстояние окрестности проверяется, чтобы определить, меньше ли оно значения параметра Максимальное расстояние окрестности или равно ему. Если новое расстояние меньше или равно максимуму, вычисления расстояния окрестности продолжаются. Если новое расстояние больше максимума, все расстояния окрестности определены и начинается вычисление отклонения.

См. раздел Как вычисляется отклонение ниже для получения дополнительной информации об этой части анализа.

Как коэффициент нелинейности влияет на расстояния окрестности

Параметр Коэффициент нелинейности управляет приращением расстояния окрестности растра. Значение по умолчанию равно 1, что приводит к линейному увеличению расстояний окрестности. Это означает, что приращения между расстояниями окрестности будут равны значению параметра Базовое приращение расстояния.

При увеличении значения параметра Коэффициент нелинейности выше 1, приращения между расстояниями окрестности изменятся после первого значения. Первое приращение будет равно значению Базовое приращение расстояния, но все последующие приращения будут постепенно увеличиваться в размере.

Если значение параметра Коэффициент нелинейности больше 1, то приращение расстояния между расстояниями окрестности после первого будет постепенно увеличиваться. Другим следствием является то, что при одинаковых минимальных и максимальных значениях окрестности более высокий коэффициент нелинейности приведет к уменьшению общего расстояния окрестностей.

На рисунке ниже показано влияние трех различных настроек параметра Коэффициент нелинейности. В этом примере используются значения 1.0, 1.5 и 2.0. Для каждой из этих настроек значения остальных параметров остаются неизменными. Значение параметра Минимальное расстояние равно 1, значение параметра Максимальное расстояние окрестности равно 10, а Базовое приращение расстояния равно 1.

Для первого приращения расстояние окрестности для всех трех настроек коэффициента нелинейности равно одному и тому же значению, то есть 2 ячейкам. После этого значения расстояния окрестности начнут меняться. Приращения будут постепенно увеличиваться при коэффициенте нелинейности, равном 1.5, и еще больше при коэффициенте, равном 2.0.

Когда значение параметра Коэффициент нелинейности равно 1.0, всего будет сделано 9 приращений, и каждое приращение будет больше предыдущего, с линейным возрастанием. При значении коэффициента 1.5, будет всего 4 приращения, а при значении 2.0 - 3 приращения.

Увеличение коэффициента нелинейности выше 1.0 приводит к постепенному увеличению размеров приращений и, следовательно, к более быстрому увеличению расстояния соседства. Это также приводит к меньшему количеству масштабов при одинаковом Минимальном расстоянии окрестности и Максимальном расстоянии окрестности, когда используется большее значение Коэффициента нелинейности.

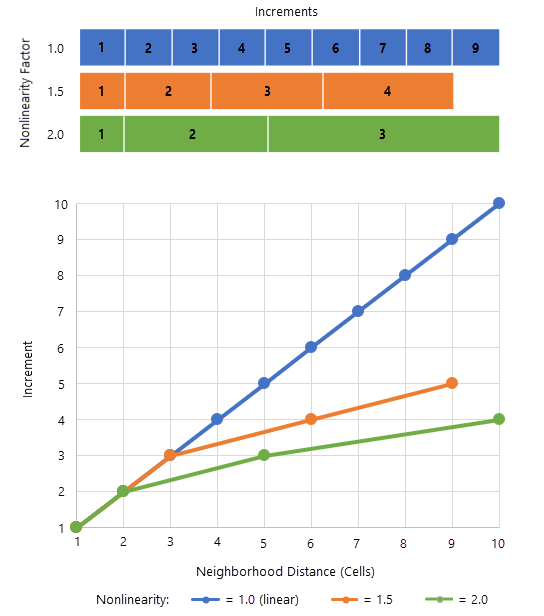
Параметр Коэффициент нелинейности позволяет настроить плотность выборки масштабов. Использование значения параметра Коэффициент нелинейности, превышающего 1.0, позволяет увеличить плотность выборки в меньших масштабах и уменьшить в больших масштабах. Однако в таких ситуациях может потребоваться увеличить значение параметра Максимальное расстояние окрестности, чтобы получить желаемое количество инкрементов. В большинстве случаев для коэффициента нелинейности используется значение от 1.0 до 2.0.

Как вычисляется отклонение

Отклонения - статистические меры, выражающие, насколько сильно значение отличается от фиксированного значения, такого как среднее по набору данных.

Для каждого определенного для вычислений расстояния окрестности и каждой ячейки во входном растре поверхности инструмент Мультимасштабное отклонение поверхности вычисляет отклонение. Максимальные значения отклонений определяются и записываются в значение параметра Выходной растр отклонений. Масштабы, при которых найдены эти отклонения, записываются как значения ячеек в параметре Выходной растр масштабов.

Чтобы вычислить отклонение, вычисляются сначала дисперсия, а затем среднеквадратическое отклонение. Эти вычисления описаны ниже.

Сначала дисперсия вычисляется для каждой ячейки. Уравнение выглядит так:

• Где:

  σ = Дисперсия значений ячейки в окрестности

  x_i = Значение ячейки i в окрестности

  n = Общее количество ячеек в окрестности (не включая ячейки NoData)

Затем, среднеквадратическое отклонение в каждой ячейке вычисляется, используя значение дисперсии. Уравнение выглядит так:

• Где:

  s_d = Среднеквадратическое отклонение значений ячейки в окрестности

  σ = Дисперсия значений ячейки в окрестности

Наконец, значение отклонения вычисляется, используя значение среднеквадратического отклонения. Уравнение выглядит так:

• Где:

  Значение отклонения = Выходное отклонение, сохраняемое для сравнения

  x_c = Исходное значение центровой ячейки в окрестности

  среднее = Среднее значений ячеек в окрестности (не включая ячейки NoData)

  s_d = Среднеквадратическое отклонение

Для эффективного вычисления средних значений используется метод интегрального изображения (Lindsay et al., 2015). При таком подходе локальные суммы окрестностей предварительно вычисляются для улучшенной производительности. Наибольшие значения отклонений определяются и записываются в значение параметра Выходной растр отклонений. Масштабы, при которых найдены эти отклонения, записываются как значения ячеек в параметре Выходной растр масштабов.

Использование графического процессора (GPU)

При установке определенных моделей графических процессоров производительность инструмента значительно повышается. Дополнительные сведения о поддержке этого механизма, его настройке и включении см. в разделе Обработка GPU с Spatial Analyst.

Список литературы

Lindsay, John B., Jaclyn M. H. Cockburn, Hanzen A. J. Russell. 2015. "An integral image approach to performing multi-scale topographic position analysis." Geomorphology Volume 245, pp. 51–61. https://doi.org/10.1016/j.geomorph.2015.05.025

Newman, Daniel R., John B. Lindsay, and Jaclyn Mary Helen Cockburn. 2018. "Evaluating metrics of local topographic position for multiscale geomorphometric analysis." Geomorphology 312, 40–50. https://doi.org/10.1016/j.geomorph.2018.04.003