Инструмент Причинно-следственный анализ оценивает причинно-следственную связь между непрерывной переменной воздействия и непрерывной переменной результата, уравновешивая искажающие переменные. Инструмент использует сопоставление оценок предрасположенности или обратное взвешивание оценок предрасположенности для назначения весов каждому наблюдению, таким образом, чтобы искажающие переменные не коррелировали с переменной воздействия, изолируя причинно-следственную связь между воздействием и результатом. Результатом является построение функции воздействие-ответ (EFR), оценивающей, как результирующая переменная реагирует на изменения в искажающих переменных. Например, вы можете оценить среднее увеличение урожайности кукурузы (результат) при различном количестве удобрений (воздействие) и исключить искажающие переменные, такие как тип почвы, принципы ведения сельского хозяйства и факотры окружающей среды, которые влияют на производство кукурузы. Функция ERF возвращается как слой графики, и отображается в сообщении геообработки. Дополнительно вы можете оценить причинно-следственную связь для отдельных наблюдений и сформировать целевые задания. Например, вы можете оценить количество удобрений, необходимое каждой ферме для производства определенного количества кукурузы в год.
Основа причинно-следственного анализа
Причинно-следственный анализ - область статистики, моделирующая отношения между воздействием и результатом для двух переменных интереса. Одна переменная (переменная воздействия или экспериментальная переменная) напрямую изменяет или влияет на другую переменную (называемую переменной результата). Корреляции часто используются для измерения, как изменения в одной переменной связаны с изменениями в другой переменной; однако корреляция не обязательно означает, что одна переменная воздействует на другую. Они обе могут находиться под влиянием других факторов. Например, продажи мороженого и солнцезащитных кремов могут иметь ярко выраженную положительную корреляцию. Но это не значит, что высокий уровень продаж мороженного повышает продажи солнцезащитных кремов. Необходимо учесть другие факторы, в частности, температуру воздуха, УФ-индекс и время года перед тем, как сделать вывод о воздействии. Факторы, влияющие как на переменную воздействия, так и на результирующую, называются искажающими переменными, и важно, чтобы они были включены и учтены для точного определения причинно-следственной связи между переменной воздействия и результата.
Причинно-следственный анализ начинается с гипотезы, основанной на исследованиях или общеизвестных фактах. Например, рассмотрим влияние физических упражнений на здоровье. Общеизвестно и доказано, что регулярные физические упражнения способствуют улучшению здоровья, но переменные также зависят от множества других сопутствующих факторов, таких как привычки в еде, выбор образа жизни и доступ к безопасным местам для занятий спортом. В таких случаях причинно-следственный анализ можно использовать для того, чтобы выделить влияние переменной воздействия (например, время, ежедневно затрачиваемое на физические упражнения) на переменную результата (например, состояние здоровья) после учета различных важных искажающих переменных.
В планируемых экспериментах искажающие переменные контролируются с помощью рандомизированных контролируемых исследований (РКИ). РКИ широко используются в клинических исследованиях, участники которых делятся на группы со схожими искажающими факторами. Каждая группа получает различный уровень воздействия, и затем сравниваются результаты. Например, участники одной группы выполняют упражнения 10 минут каждый день, другой - 1 час каждый день, и третья группа совсем не занимается спортом. Так как предполагается, что во всех группах одинаковый уровень искажающих переменных, любые различия в результирующем оценивании состояния здоровья не могут быть вызваны влиянием искажающих переменных. Если все значимые искажающие переменные корректно присутствуют в плане эксперимента, отличия в результате могут быть вызваны только различными воздействиями (например, количеством ежедневных упражнений).
Однако в реальных сценариях часто невозможно или неэтично создавать корректные контрольные экспериментальные группы. Например, при изучении влияния загрязнения воздуха на депрессию, не этично намеренно подвергать людей воздействию сильного загрязнения, чтобы оценить насколько выраженна у них депрессия. Вы только можете наблюдать за уровнем загрязнения в той или иной области, и оценивать уровень депрессии. Причинно-следственный анализ может быть использован для моделирования причинно-следственных отношений на основе данных наблюдений, полученных при имитации планируемого контролируемого эксперимента. Это выполняется путем оценивания предрасположенности для каждого наблюдения и полученные оценки предрасположенности используются для присвоения весов балансировки каждому наблюдению. Веса балансировки сконфигурированы таким образом, что они поддерживают причинно-следственные отношения между переменными воздействия и результата, но устраняют влияние искажающих переменных на переменную воздействия, позволяя непредвзято оценить причинно-следственное отношение. Результирующие взвешенные наблюдения обладают свойствами, аналогичными свойствам набора данных, собранного с помощью РКИ, и вы можете делать по тому же принципу, что и для наборов данных, собранных с помощью планируемых экспериментов.
Существуют два стандартных метода оценки весов балансировки - сопоставление оценок предрасположенности и обратное взвешивание оценок предрасположенности. При сопоставлении оценок предрасположенности каждое наблюдение сопоставляется с различными другими наблюдениями со схожим набором искажающих переменных (оцениваемых по подобию их оценок предрасположенности) но с различными значениями воздействия. Сравнивая результирующие значения наблюдений с результирующими значениями сопоставления вы можете понять, какое значение результата наблюдения будет при различном воздействии. Вес балансировки, назначаемый каждому наблюдению, равен числу раз, когда наблюдение совпадало с каким-либо другим наблюдением. При обратном взвешивании оценок предрасположенности веса балансировки присваиваются путем инвертирования оценки предрасположенности и умножения этого значения на общую вероятность воздействия. Этот процесс увеличивает представление нераспространенных наблюдений (наблюдений с низкими оценками предрасположенности) и снижает представление распространенных наблюдений (наблюдений с высокими оценками предрасположенности), таким образом доля влияния искажающих переменных сохраняется для всех значений переменной воздействия.
Веса балансировки, определенные сопоставлением оценок предрасположенности или обратным взвешиванием оценок предрасположенности не всегда успешно уравновешивают искажающие переменные, поэтому их взвешенные корреляции при вычислении сравниваются с пороговым значением. Если корреляции ниже порогового значения (то есть, низкая корреляция), то считается, что они сбалансированы, и оценивается ERF. Если веса балансировки недостаточно уравновешивают баланс в искажающих переменных, инструмент вернет ошибку и ERF не будет создана.
Примеры применения
Ниже примеры использования инструмента:
- Исследование влияния рекламы табачных изделий на употребление табака подростками в Соединенных Штатах. В этом примере переменная воздействия - это степень воздействия рекламы на каждого подростка, а переменная результата - количество табака, потребляемого каждым подростком за определенный период времени. Искажающими переменными могут быть любые другие переменные, точно или возможно связанные с воздействием или с употреблением табачных изделий подростками, такие как социально-экономические факторы, курение в семье или в компании, цена и доступность табачных изделий. Для исследования употребления табака подростками можно было бы выбрать множество переменных воздействия (например, прямое воздействие табачных изделий на членов семьи), но реклама табачных изделий является очевидным воздействием. Так как доказано, что большое количество рекламы приводит к значительному увеличению потребления табака подростками, применяется регулирование для снижения объема рекламы. Сократить потребление тобака взрослыми значительно сложнее.
- Оценка причинно-следственной связи количества удобрений и урожайности кукурузы в условиях точного земледелия, с учетом типов почв, методов ведения сельского хозяйства, факторов окружающей среды и других искажающих переменные для каждого фермерского хозяйства. Например, сколько дополнительного урожая кукурузы можно было бы снять, если бы каждая ферма увеличила количество удобрений на 10 процентов?
- Оценка причинно-следственной связи между артериальным давлением и риском сердечно-сосудистых заболеваний, с учетом таких искажающих переменных, как возраст, вес, социально-демографические условия и доступ к медицинскому обслуживанию.
- В пространственных данных расстояния до других объектов - эффективные переменные воздействия. Например, расстояние до продуктовых магазинов, парков и больниц вызывает изменения в других переменных: расстояние до продуктового магазина сокращает доступ к продуктам питания, расстояние до больницы сокращает доступ к медицинскому обслуживанию и так далее. По тем же причинам пространственные переменные и расстояния до других объектов также часто являются важными искажающими переменными, даже если переменные воздействия и результата не являются пространственными переменными.
Тем не менее причинно-следственный анализ имеет ряд ограничений и допущений, которые должны учтены, чтобы оценки причинно-следственных связей были объективными и достоверными. Ниже ряд допущений и ограничений для причинно-следственного анализа.
- Все значимые искажающие переменные должны быть учтены. Это жесткое допущение причинно-следственного анализа, то есть, если какие-либо переменные, связанные как с переменной воздействия, так и с переменной результата, не включены в модель как искажающие переменные, оценка причинно-следственного эффекта будет смещена (смешивание причинно-следственного эффекта и искажающего эффекта любых отсутствующих искажающих переменных). Инструмент не может определить, все ли значимые переменные включены, поэтому очень важно, чтобы вы решили, какие искажающие переменные следует включить. Если существуют значимые искажающие переменные, которые недоступны, интерпретируйте результаты инструмента с особой осторожностью, или не используйте инструмент.
- Корреляции между искажающими переменными и переменной воздействия должны быть удалены, чтобы изолировать причинно-следственную связь. В причинно-следственном анализе удаление корреляций между искажающими переменными и переменными воздействия называется - балансировка, и инструмент использует различные методы для этого. Полностью удалить корреляции между искажающими переменными и переменными воздействия бывает невозможно. Если методы балансировки недостаточно уравновешивают баланс в искажающих переменных, инструмент вернет ошибку и ERF не будет создана. Подробную информацию об ошибках и их решении см. Советы по получению сбалансированных искажающих переменных.
- ERF не может экстраполировать за пределами диапазона значений воздействия, которые были использованы для оценки. Например, если переменной воздействия является среднегодовая температура, вы не сможете оценить новые результаты для температур, превышающих указанные в выборке. Это означает, в частности, что вы не сможете предсказать результаты в будущем, когда средние значения температуры, скорее всего, будут превышать текущие средние значения температуры. Дополнительно инструмент сокращает (удаляет из анализа) нижний 1 процент значений воздействия по умолчанию, поэтому диапазон ERF будет даже меньше, чем диапазон переменных воздействия наблюдений в выборке.
Выходные данные инструмента
Инструмент создает различные результаты, которые можно использовать для изучения причинно-следственных отношений между переменными воздействия и результата. Результаты возвращаются в виде слоя графики, сообщений геообработки, выходного класса объектов (или таблицы), и выходной таблицы ERF.
Функция воздействие-ответ
Основным результатом инструмента является EFR, которая оценивает, как результирующая переменная реагирует на изменения в искажающих переменных. ERF оценивает новое среднее в популяции (среднее для всех участников в совокупности) переменной результата, если все участники совокупности изменились, из-за одной и той же переменной воздействия, но сохранили все существующие искажающие переменные. Например, для всех округов США, если переменная воздействия равна PM2,5, а переменная результата - частота госпитализаций при астме, ERF оценивает, как изменился бы средний показатель госпитализации при астме в популяции, если бы общий уровень PM2,5 был увеличен или уменьшен при сохранении всех других переменных (таких как социально-демографические факторы) на прежнем уровне, до изменения PM2.5.
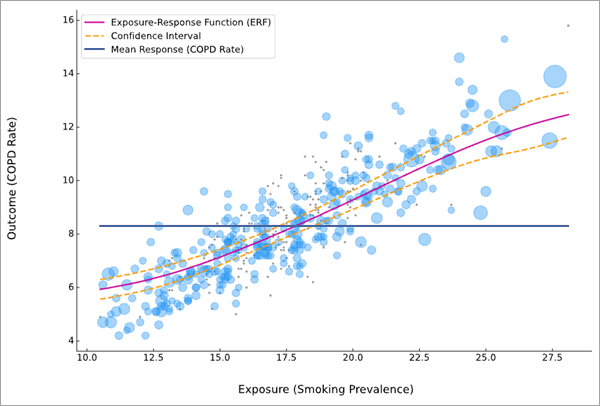
Если запущена активная карта, слой графики будет добавлен к карте, отображающий ERF. То же изображение ERF показывается в сообщении.
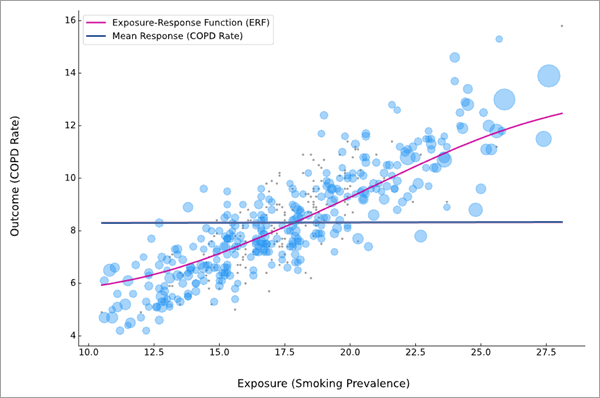
Розовая кривая - это ERF между переменными воздействия (ось x) и результата (ось y). Наблюдения показаны в виде светло-голубых пузырьков на заднем плане диаграммы рассеяния, более крупные пузырьки указывают на то, что объект имел больший вес балансировки и внес максимальный вклад в оценку ERF. При сопоставлении оценок предрасположенности, если наблюдения не сопоставлены, они отображаются светло-серыми точками. Сокращенные наблюдения не показываются на диаграмме.
ERF также содержит голубую горизонтальную линию, показывающую среднее значение переменной результата, чтобы его можно было сравнить со средней оценкой для разных уровней переменной воздействия. Например, на рисунке выше, если бы все округа изменили свою распространенность курения на одинаковое значение, примерно ниже 17,5 (где средняя линия пересекает ERF), общий уровень ХОБЛ снизился бы по сравнению с текущим уровнем. Аналогичным образом, общий показатель ХОБЛ увеличился бы, если бы во всех странах распространенность курения превысила 17,5.
Вы можете также использовать параметр Выходная таблица функции воздействие-ответ, для создания таблицы ERF. Если создается, таблица будет содержать 200 равномерно распределенных значений воздействия между минимальным и максимальным воздействием вместе с соответствующим значением результата. Если указаны какие-либо значения целевого результата или целевого воздействия, они будут добавлены в конце этой таблицы.
Более подробно о статистике балансировки искажающих переменных.
Раздел Результаты балансировки в сообщениях показывает исходную и взвешенную абсолютные корреляции между каждой искажающей переменной и значением воздействия. Это позволяет вам увидеть, будут ли веса балансировки эффективно уменьшать исходные корреляции между искажающими переменными и переменной воздействия. Если веса эффективны при балансировке, взвешенные корреляции будут меньше исходных корреляций. Последняя строка в таблице сообщений содержит среднюю, медианную или максимальную абсолютную корреляцию, зависимую от значения параметра Тип балансировки.
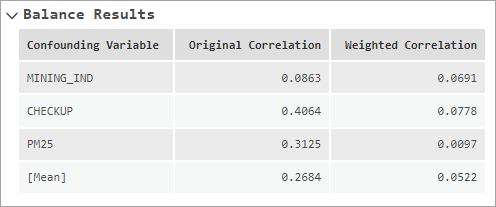
Диаграмма в сообщении Корреляция между искажающими переменными и воздействием показывает информацию в виде таблицы, кроме диаграммы - вертикального графика. Для каждой искажающей переменной исходные корреляции соединены красной линий, а взвешенные корреляции - голубой. Исходные и взвешенные агрегированные корреляции также отображаются как голубые и красные столбики, соответственно. Если веса эффективно уравновешивают искажающие переменные, линии голубого цвета, в основном будут слева от красных. Порог баланса показывается вертикальной пунктирной линией, позволяя увидеть, насколько корреляции приближаются к порогу. Например, на изображении ниже две искажающих переменных начинаются с относительно высоких корреляций (выше 0.3 и 0.4 соответственно), но вес абалансировки снижают значения корреляций до 0.1. Третья искажающая переменная начинается с низкого значения корреляции (чуть ниже 0.1), но веса балансировки еще больше уменьшают ее. В общем, средняя корреляция снижается с 0.3 до 0.1.
См. раздел Проверка наличия сбалансированных искажающих переменных ниже для дополнительной информации о балансе искажающих переменных.
Результаты настройки параметров
Сообщение также содержит разделы, в которых суммируются разнообразные настройки параметров, используемые для оценки ERF. В зависимости от параметров, указанных в инструменте, могут быть показаны следующие разделы:
- Результаты сокращения — отображается исходное число наблюдений (после удаления записей со значением null), число наблюдений, удаленных по сокращению воздействия, число наблюдений, сокращенных по оценке предрасположенности и окончательное число наблюдений, которое осталось после сокращений.
- Сетка сопоставлений результатов поиска — для сопоставления оценок предрасположенности показаны результаты поиска параметров сопоставления. Инструмент использует разнообразные комбинации числа бинов воздействия и относительных весов оценки предрасположенности к воздействию (масштабирование) и отображает результирующие взвешенные корреляции для каждой комбинации. Комбинации, при которых отмечается минимальная взвешенная корреляция (оптимальный баланс) - выделена жирным шрифтом.
- Показаны преобразования сбалансированных результатов — для модели регрессии оценок предрасположенности преобразования искажающих переменных, которые были использованы для нахождения баланса, а также взвешенная корреляция для каждой комбинации преобразования. Комбинация преобразования, при которых отмечается минимальная взвешенная корреляция - выделена жирным шрифтом.
- Результаты балансировки градиентного бустинга — для модели оценок предрасположенности градиентного бустинга будет показана сетка результатов поиска градиентного бустинга. Инструмент пробует девять комбинаций количеств деревьев и скоростей обучения, и отображает результирующие взвешенные корреляции для каждой комбинации. Комбинации, при которых отмечается минимальная взвешенная корреляция, выделена жирным шрифтом.
- Параметры, определяющие оптимальный баланс — для сопоставления оценок предрасположенности показано число бинов воздействия и относительный вес оценки предрасположенности к переменной воздействия (масштабирование), при которых достигается оптимальный баланс искажающих переменных. Для градиентного бустинга отображается число деревьев, скорость обучения и случайным образом генерируемое исходное значение, приводящее к оптимальному балансу.
- Результат балансировки — отображаются исходные и взвешенные переменные для каждой искажающей переменной, а также средняя, медианная и максимальная корреляции. Если применялись преобразования, для каждой искажающей переменной преобразование также будет показано.
См. раздел Оценка оптимальных параметров балансировки ниже для подробной информации, сколько значений в сообщениях выделено.
Выходные объекты
Выходные объекты или таблица, содержащая копии переменной воздействия, переменной результата и искажающих переменных, а также оценки предрасположенности, веса балансировки (количество сопоставлений или обратное взвешивание оценок предрасположенности), и поле, указывающее, была ли запись сокращена. При добавлении на карту выходные объекты отображаются в соответствии с весами балансировки. Это позволит вам увидеть, есть ли какие-либо пространственные закономерности в весах, указывающие на то, что какие-либо регионы излишне или недостаточно представлены в результатах.
Если вы указываете какое-либо целевое значения воздействия или результата, для каждого указанного значения будут созданы два новых поля в выходных данных. Для целевых значений воздействия первое поле содержит значение результата, определенное, исходя из того, что наблюдение получило целевое воздействие, а второе поле содержит прогнозируемое изменение в переменной результата. Положительное значение указывает, что переменная результата увеличивается, а отрицательное значение указывает на уменьшение переменной результата Для целевых значений результата первое поле содержит значение воздействия, которое должно привести к целевому результату, а второе поле содержит прогнозируемое изменение в переменной для получения целевого результата.
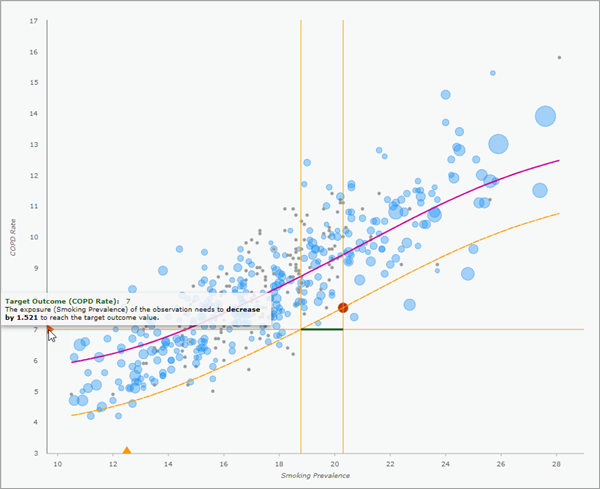
Если вы создаете диаграммы локальных ERF во всплывающих окнах, для каждой выходной записи будет показана локальная ERF во всплывающем окне. Все переменные воздействия или результата показаны оранжевыми треугольниками на осях x- и y-. Вы можете щелкнуть треугольник, чтобы показать/скрыть горизонтальные или вертикальные столбцы, и увидеть, какое значение пересекает локальную ERF. Дополнительно вы можете навести курсор на треугольник, чтобы увидеть информацию о необходимых для достижения цели изменениях в воздействии или в результате. См. Оценка локальной причинно-следственной связи для дополнительной информации.
Если вы создаете начальные доверительные интервалы для ERF, будут добавлены два дополнительных поля, содержащие количество раз, когда наблюдение присутствует в выборке начального интервала, и количество раз, когда наблюдение включено в выборку начального интервала, в которой выровнен баланс. Рекомендуется оценить пространственные закономерности в обоих полях. Если некоторые регионы содержат существенно больше сбалансированных начальных выборок, доверительные интервалы могут быть смещены (обычно это приводит к нереалистично узким доверительным интервалам). См. Начальные доверительные интервалы для дополнительной информации.
Оценки предрасположенности
Основа причинно-следственного анализа - оценки предрасположенности. Оценка предрасположенности представляет собой правдоподобие (или вероятность), того, что наблюдение получит определяемое значение при данном воздействии и заданных значениях искажающих переменных. Высокие оценки предрасположенности означают, что значение воздействия является типичным для индивидуумов со схожим набором значений искажающих переменных, а низкие оценки предрасположенности означают, что такое воздействие не типично для индивидуумов с этими значениями искажающих переменных. Например, если у человека высокое артериальное давление (переменная воздействия), но у него нет факторов риска гипертензии (искажающие переменные), у него будет низкая оценка предрасположенности, так как высокое артериальное давление без каких-либо факторов риска встречается редко. Соответственно высокое давление для человека в зоне риска приведет к высоким значениям оценки предрасположенными, так как это типичная ситуация.
Для анализа причинно-следственной связи используются два подхода - сопоставлении оценок предрасположенности и обратном взвешивании оценок предрасположенности. Каждый подход предполагает назначение весов балансировки каждому наблюдению, и затем использование их для уравновешивания искажающих переменных (см. раздел Проверка наличия сбалансированных искажающих переменных ниже для дополнительной информации).
Сопоставление оценок предрасположенности
Сопоставление оценок предрасположенности направлено на достижение баланса искажающих переменных путем сопоставления каждого наблюдения — с различными другими наблюдениями со схожим набором значений искажающих переменных, но различными значениями воздействия. Сравнивая результирующие значения наблюдений с результирующими значениями сопоставленных наблюдений, вы увидите, какое значение результата наблюдения должно быть при различном воздействии (но с одинаковыми искажающими переменными). После нахождения сопоставлений для всех наблюдений, вес балансировки, назначаемый каждому наблюдению, равен числу раз, когда наблюдение совпадало с каким-либо другим наблюдением. Например, если наблюдение не сопоставилось ни с каким другим наблюдением, вес балансировки будет равным нулю, а если наблюдение сопоставлено со всеми остальными наблюдениями, вес балансировки вес балансировки будет равен числу наблюдений.
Сопоставление оценок предрасположенности для переменной воздействия непрерывного типа относительно сложный процесс - он подробно описан в 4м и 5м пунктах списка литературы ниже. Ниже краткое описание процесса сопоставления:
Сначала наблюдения разделяются на пространственно равные бины по значениям переменной воздействия (как бины в гистограмме), на основании значения параметра Число бинов воздействия. Сопоставление оценок предрасположенности выполняется внутри каждого бина путем сравнения оценок предрасположенности наблюдений внутри бина с гипотетическими оценками предрасположенности всех остальных наблюдений. Гипотетические оценки предрасположенности, это оценки, которые наблюдение должно было бы получить, если бы сопровождалось теми же искажающими переменными, но с другим воздействием (в этом случае, центральное значение каждого бина воздействия). Сопоставление внутри каждого бина определяется нахождением наблюдения в бине воздействия, оценка предрасположенности которого приближена к гипотетическим оценкам предрасположенности всех остальных наблюдений. Тем не менее, так как значения воздействия наблюдений в бине обычно не выровнены по центру бина, добавляется дополнительное компенсирующее значение, на основании разницы между значением воздействия и центром бина воздействия. Сумма компенсаций определяется значением Относительного веса оценки предрасположенности к воздействию (в справочниках он называется параметром масштабирования), а общим совпадением считается наблюдение с наименьшей взвешенной суммой абсолютных различий в оценках предрасположенности (оценка предрасположенности минус гипотетическая оценка предрасположенности) и воздействии (необработанное воздействие минус значение центра бина).
Обратное взвешивание оценок предрасположенности
Обратное взвешивание оценок предрасположенности — веса балансировки присваиваются каждому наблюдению путем инвертирования оценки предрасположенности и умножения этого значения на общую вероятность наличия данного воздействия. В этом варианте причинно-следственного анализа наблюдения с низкой оценкой предрасположенности получают высокие значения весов балансировки, а наблюдения с высокой оценкой предрасположенности - соответственно низкие веса балансировки. Эта схема весов основывается на постулате, что оценки предрасположенности измеряют, насколько распространено или не распространено значение воздействия для конкретного набора искажающих переменных. При повышении влияния (увеличении веса балансировки) нераспространенных наблюдений (наблюдений с низкими оценками предрасположенности) и снижении влияния распространенных наблюдений, пропорция общего распределения искажающих переменных сохраняется для всех значений переменной воздействия.
Примечание:
Оценка плотности ядер (KDE) используется для оценки общей вероятности значения воздействия. KDE использует ядро Гаусса с шириной полосы Сльвермана, встроенное в функцию scipy.stats.gaussian_kde пакета SciPy Python.
Вычисление оценок предрасположенности
Параметр Метод вычисления оценки предрасположенности к воздействию дает определяет, как будут вычисляться оценки предрасположенности. Каждый метод строит модель, использующую искажающие переменные как независимые переменные, а переменную воздействия - как зависимую. Доступны два метода вычисления оценки предрасположенности:
- Регрессия — для вычисления оценок предрасположенности будет использована регрессия по методу наименьших квадратов (МНК).
- Градиентный бустинг — для вычисления оценок предрасположенности будет использовано дерево регрессии с градиентным бустингом.
Для модели регрессии прогнозированные значения - это присвоенные вероятности, предполагающие нормально распределенные стандартизированные невязки. Модель градиентного бустинга сама по себе не вычисляет стандартизированные невязки, поэтому инструмент строит вторую модель градиентного бустинга для прогнозирования абсолютных значений невязок для первой модели, что обеспечивает оценку стандартной ошибки. KDE (так же, как обратное взвешивание оценок предрасположенности выше) использует стандартизированные невязки для вычисления распределения стандартизированных невязок. Это распределение затем можно использовать для вычисления оценок предрасположенности для всех сочетаний значений переменных воздействия и искажающих переменных.
И регрессия, и градиентный бустинг пересчитывают переменные в диапазон от 0 до 1 перед построением для них соответствующих моделей.
Проверка сбалансированных искажающих переменных
Чтобы ERF без смещения оценивала причинно-следственную связь, все искажающие переменные должны быть включены и сбалансированы, то есть искажающие переменные не должны коррелировать с переменной воздействия. Так как искажающие переменные коррелируют с переменной воздействия по определению, исходные искажающие переменные всегда будут не сбалансированы. Тем не менее смысл весов балансировки (по числу совпадений оценок предрасположенности или по обратному взвешиванию оценок предрасположенности) - взвесить каждое наблюдение таким образом, чтобы взвешенные наблюдения стали сбалансированными, но причинно-следственная связь между переменными воздействия и переменными результата сохраняется, что позволяет объективно оценить ERF.
Чтобы выявить, насколько веса балансировки хорошо уравновешивают искажающие переменные, вычисляются взвешенные корреляции между искажающей переменной и переменной воздействия. Абсолютные значения взвешенных корреляций затем агрегируются и сравниваются с пороговым значением. Если значение агрегированной корреляции меньше порогового, искажающие переменные будут считаться сбалансированными. Вы можете выбрать тип агрегации (среднее, медиана или максимум абсолютной корреляции), используя параметр Тип баланса и указав пороговое значение в параметре Порог баланса. По умолчанию инструмент вычисляет среднюю абсолютную корреляцию и использует пороговое значение в 0.1.
Примечание:
Для искажающих переменных непрерывного типа при расчете взвешенных корреляций используется алгоритм ранжированного коэффициента корреляции Спирмана. Эта корреляция рассчитывается подобно традиционному коэффициенту корреляции Пирсона, но использует взвешенное ранжирование переменных вместо необработанных значений. Ранжирование делает расчет корреляций более устойчивым к выбросам и асимметричным распределениям. Для искажающих переменных категорийного типа при расчете взвешенных корреляций используется взвешенной статистики eta, которая использует взвешенное ранжирование переменной воздействия. Статистика eta практически эквивалентна абсолютной корреляции Пирсона для категорийных переменных (оба представляют собой квадратный корень из квадрата коэффициента детерминации), и использование взвешенного ранжирования необработанных значений приближает его к абсолютным значениями взвешенных корреляций Спирмана.
Советы по достижению сбалансированных искажающих переменных
Если веса балансировки недостаточно уравновешивают баланс в искажающих переменных, инструмент вернет ошибку и не создаст ERF, но вы увидите ряд сообщений с информацией о взвешенных корреляциях каждой искажающей переменной. Если такая ошибка произойдет, просмотрите сообщения, чтобы определить, насколько веса балансировки уменьшали корреляции и насколько близка была взвешенная корреляция к пороговому значению баланса.
Если инструмент не сможет достигнуть баланса, подумайте, не упустили ли вы какие-либо искажающие переменные, и включите те, которых не зватает. Далее попробуйте различные опции для параметров Метод расчета оценки предрасположенности и Метод балансировки. Однако для некоторых наборов данных может отсутствовать сочетание, обеспечивающее баланс.
В целом, чем выше значения исходных корреляций между искажающими переменными, тем сложнее их сбалансировать. Для высоко коррелированных искажающих переменных для достижения уверенного баланса могут потребоваться выборки большого размера. Для искажающих переменных категорийного типа, чем больше категорий, тем сложнее их сбалансировать. Может потребоваться комбинация некоторых категорий, особенно если есть некоторая вариабельность переменной воздействия или небольшое число наблюдений (как правило, меньше 5) в каждой категории.
Однако, если вы можете допустить внесение смещения в ERF, вы можете достигнуть баланса, увеличивая пороговое значение баланса или используя более мягкий тип баланса.
В основном более низкое пороговое значение баланса указывает на меньшую допустимость смещения при оценке причинно-следственной связи; но при более низких пороговых значениях достичь баланса сложнее. Для типа баланса использование среднего значения корреляций гарантирует, что искажающие переменные сбалансированы по среднему, но это все равно позволяет некоторым искажающим переменным с высокими значениями корреляций, в сочетании с достаточным количеством искажающих переменных с низкими значениями корреляций получить среднее значение ниже порога. Опция максимальной корреляции наиболее консервативна, и требует, чтобы все искажающие переменные были со значениями ниже порогового. Даже если одна искажающая переменная чуть выше порога, балан искажающих переменных не будет достигнут. Медианный вариант является наиболее мягким, и он допускает до половины корреляций с высокими значениями, с возможностью, при этом, достижения баланса.
Поиск оптимальных параметров балансировки
Достижение баланса искажающих переменных часто затруднено, поэтому инструмент пробует разнообразные метод оптимизации и подбирает параметры таким образом, чтобы насколько возможно сбалансировать искажающие переменные. Выполняемые оптимизации также зависят то множества параметров инструмента, которые описаны в разделах ниже.
Поиск параметров сопоставления
При сопоставлении оценок результаты сопоставления зависят от значений в параметрах Число бинов воздействия и Относительный вес оценки предрасположенности к переменной воздействия, но прогнозировать значения, показывающие оптимальный баланс затруднительно. Кроме того, небольшие изменения в одном из значений могут привести к большим изменениям в другом, поэтому особенно трудно найти пару значений, которая работает эффективно. Если значения для параметров не указаны, инструмент будет попробовать различные комбинации, и результаты будут показаны в виде таблицы в сообщении. В этой таблице строки представляют собой число бинов воздействия, а столбцы - относительные веса (иногда называемые - масштабирование). Взвешенные корреляции каждой комбинации показаны в виде сетки, и каждая комбинация, при которой достигнут оптимальный баланс, будет отмечена звездочкой рядом со значением. Комбинации, при которых отмечается минимальная взвешенная корреляция (оптимальный баланс) - выделена жирным шрифтом. Как показано на рисунке ниже, взвешенные корреляции могут существенно различаться при различных значениях двух параметров.
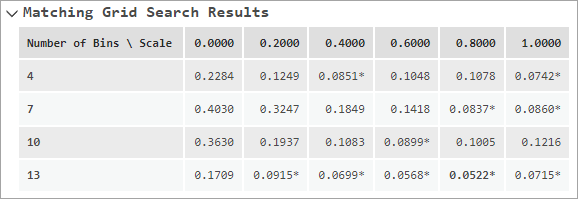
Инструмент пробует использовать относительные веса в диапазоне от 0 до 1 с шагом 0.2, но количество тестируемых бинов воздействия зависит от количества наблюдений. Протестированные значения находятся в диапазоне от корня четвертой степени до двукратного кубического корня из числа наблюдений. Тестируемые значения будут увеличиваться равномерно, с шагом не менее трех, при этом будет тестировано не более 10 значений.
Преобразования регрессии
При использовании регрессии для вычисления оценок предрасположенности, если искажающие переменные не сбалансированы, к непрерывным переменным ним могут быть применены раздичные преобразования. Если в какой-то момент искажающие переменные достигли баланса, процесс прекращается и текущий набор преобразования будет использован для построения ERF.
Процесс начинается с искажающей переменной, которая является наименее сбалансированной (максимальная взвешенная корреляция), и использует последовательность преобразований. Преобразование, при котором достигнут баланс, сохраняется, и процесс повторяется со следующей искажающей переменной. Процесс продолжается, пока все искажающие переменные не будут протестированы со всеми преобразованиями, и если искажающие переменные все еще не сбалансированы, инструмент вернет ошибку и не построит ERF.
Будут применены следующие преобразования с некоторыми ограничениями для значений искажающих переменных, предназначенных для преобразования:
- Натуральный логарифм — только для искажающих переменных с положительными значениями
- Квадрат — только для искажающих переменных с не отрицательными значениями
- Квадратный корень — только для искажающих переменных с не отрицательными значениями
- Куб
- Кубический корень
Преобразования, с которыми достигнут оптимальный баланс, будут указаны в разделе Результаты баланса в сообщениях, а вся история примененных преобразований - в разделе Результаты балансировки преобразования.
При сопоставлении оценок предрасположенности число бинов воздействия и относительный вес значений исходных (не преобразованных) искажающих переменных будет использован для всех комбинаций преобразования. Это делается для предотвращения очень длительного времени вычислений путем повторения поиска соответствующих параметров для каждой комбинации преобразований. Квадратичное преобразование ограничено неотрицательными значениями, так что порядок значений воздействия не меняется до и после преобразования, что важно при повторном использовании числа бинов воздействия и относительного веса, определенных по исходным наблюдениям.
Поиск параметров градиентного бустинга
При использовании градиентного бустинга для вычисления оценок предрасположенности, будут протестированы разнообразные комбинации количества деревьев и скорости обучения. Если в какой-то момент искажающие переменные достигли баланса, процесс прекращается и используются текущее количество деревьев и скорость обучения. Инструмент пробует до девяти комбинаций: количество деревьев, равное 10, 20 и 30 деревьев, и скорости обучения, равные 0.1, 0.2 и 0.3.
Количество деревьев и скорость обучения, с которыми достигнут оптимальный баланс, будут указаны в разделе Параметры, обеспечивающие наилучший баланс в сообщениях, а вся история комбинаций параметров - в разделе Результаты балансировки градиентного бустинга.
В отличие от преобразований регрессии, поиск параметров сопоставления для бинов воздействия и относительных весов будет повторяться для каждой комбинации количества деревьев и скорости обучения. Более глубокий поиск выполняется, так как небольшие изменения любого из этих четырех параметров могут вызывать значительные изменения в оптимальных значениях для остальных.
Оценка функции воздействие-ответ
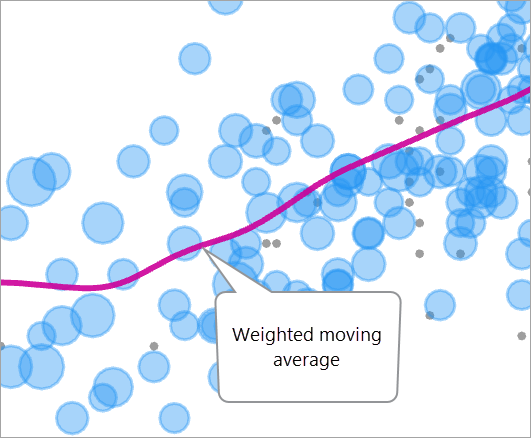
В процессе балансировки назначаются веса балансировки (совпадающие количества или обратные веса оценок предрасположенности) каждому наблюдению, и эти веса являются основой для формирования функции воздействие-ответ. Каждое взвешенное наблюдение (иногда они называются псевдосовокупности) содержат значение воздействия, значение результата и вес, и используется для подгонки сглаженной кривой (ERF) к значениям взвешенных наблюдений. При вычислении оценок ERF каждое наблюдение влияет на оценку пропорционально его весу. Другими словами, наблюдение с весом, равным трем, влияет так же, как и три наблюдения, каждое из которых имеет вес, равный единице. И так же, наблюдение с нулевым весом не будет влиять на ERF, эффективно отфильтровывая наблюдения.
Для данного значения переменной воздействия (ось x), связанное значение ответа (ось y) оценивается как взвешенное скользящее среднее (иногда называемое сглаживающее ядро) значений результатов наблюдений. Веса во взвешенном среднем - это веса балансировки, умноженные на вес Гауссова ядра, сокращенный до трех среднеквадратических отклонений.
Когда эта процедура выполнена для всех значений переменной воздействия, результатом будет сглаженная кривая, которая проходит через наблюдения, вытягиваясь в сторону наблюдений с большими весами.
Оценка ширины полосы
Ядро в формуле ERF зависит от значения ширины полосы (среднеквадратического отклонения Гауссова ядра), которое определяет сглаженность кривой ERF, и подбор подходящего значения ширины полосы крайне важно для реалистичной и точной ERF. Большие значения ширины полосы приводят к более сглаженной ERF при одинаковом наборе взвешенных наблюдений. На следующем рисунке показаны три значения ширины полосы, используемые для одинаковых наблюдений:
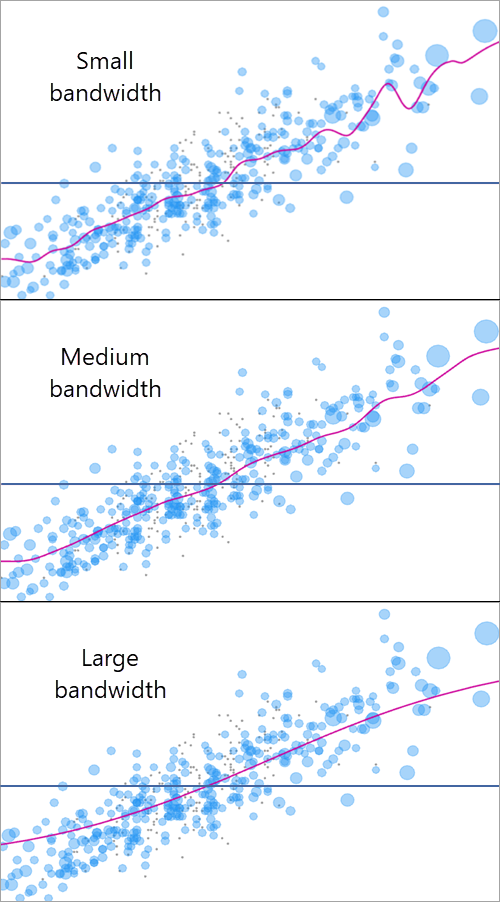
Вы можете использовать параметр Метод оценки ширины полосы для определения подбора значения ширины полосы. Доступны три метода оценки ширины полосы:
- Надстройка — быстрая эмпирическая формула используется для оценки значения ширины полосы. Используется по умолчанию, вычисляется быстро и обчыно при этом получаются точные и реалистичные ERF. Метод представляет собой взвешенный вариант методологии Фана (1996), и выводит значение ширины полосы из второй производной взвешенного глобального полинома четвертого порядка, подогнанного ко всем наблюдениям.
- Перекрестная проверка — используется ширина полосы, при который минимизируется среднеквадратичная ошибка перекрестной проверки. Опция требует больше времени для вычисления, но лучше всего отвечает статистической теории. Тем не менее, для больших наборов данных перекрестная проверка имеет тенденцию к очень небольшим значениям ширины полосы, приводящим к очень искривленным ERF.
- Вручную — будет использовано пользовательское значение Ширины полосы. Эта опция рекомендуется, если другие опции назначения ширины полосы приводят к очень сглаженным, или очень искривленным ERF. Рекомендуется проанализировать значения ширины полосы, полученные другими методами, и выполнить некоторую корректировку, чтобы подогнать сглаженность.
Присвоенное значение ширины полосы будет указано в нижней части сообщения.
Примечание:
В методах надстройки и перекрестной проверки, если оцененное значение ширины полосы меньше наибольшего промежутка между значениями воздействия, вместо него будет оцениваться наибольший промежуток. Это делается для гарантии того, что каждое значение воздействия содержит достаточно данных для получения средневзвешенного значения. Для использования меньшего значения ширины полосы укажите его вручную.
Оценка локальной причинно-следственной связи
Вы можете создавать локальные ERF для каждой записи выходных объектов или таблицы, отметив параметр Включить всплывающие окна воздействие-ответ. Если опция отмечена, выходные данные будут включать диаграмму ERF во всплывающем окне каждого объекта или записи таблицы. Выплывающее окно показывает, как переменная результата для отдельного наблюдения оценивается при изменениях переменной воздействия. Локальная ERF использует ту же форму, что и глобальная ERF, но сдвигается выше или ниже, чтобы пройти через отдельное наблюдение. Дополнительно, если указано целевое значение результата или воздействия, они будут показаны в диаграмме всплывающего окна, вместе с изменениями, которые необходимо внести в воздействие или результат, чтобы получить целевое значение наблюдения.
Создание локальных ERF, или использование целевых значений воздействия или результата требует допущения наличия фиксированного эффекта воздействия для всех наблюдений. Это строгое допущение, и нарушение его может привести к смещенным или неверным результатам. Допущение фиксированного эффекта воздействия подразумевает, что эффект воздействие - результат постояннен для всех индивидуумов в совокупности. Другими словами, взяв начальное воздействие, и повышая его на фиксированную величину, мы получим одинаково изменившийся результат для всех, независимо от уровня остальных переменных (включая измеренные искажающие переменные, но не только). Например, увеличение количества удобрений со 150 фунтов на акр до 175 фунтов на акр привело бы к увеличению урожайности кукурузы на одинаковую величину на всех фермах, независимо от их текущей показателей урожайности, типа почвы, методов ведения сельского хозяйства или других сопутствующих переменных.
Это предположение разумно, если отсутствуют модификаторы эффекта, то есть переменные, влияющие на то, как результат реагирует на воздействие для отдельных индивидуумов. Но социально-демографические переменные, такие как пол, раса или уровень образования, часто являются модификаторами эффекта, и именно они обычно являются искажающими переменными в модели причинно-следственных связей. Это хорошо работает для усреднения изменения эффекта по всем уровням модифицирующей переменной, позволяя оценить глобальную усредненную причинно-следственную связь (ERF). Но глобальная ERF не представляет какую-либо конкретную подгруппу, определяемую уровнями модификатора эффекта. Например, программы по повышению квалификации могут показать увеличение числа предложений о работе с ростом количества часов обучения. Но в районах, где преобладают афроамериканское или испаноязычное население, число предложений о работе снижается после определенных часов обучения, что потенциально предполагает дискриминацию по расовому или национальному признаку при приеме на работу. Таким образом, глобальная ERF может непреднамеренно скрывать различия, с которыми сталкиваются эти сообщества. То есть глобальная ERF представляет усредненный эффект воздействия на результат для всей совокупности; но в случае наличия модифицирующих эффект переменных глобальная ERF может не точно воспроизводить эффект воздействия на результат, в особенности в определенных областях (например, проживания афроамериканцев или латиноамериканцев).
Локальные ERF не корректны, если модель содержит модификаторы эффектов. Одним из подходов к работе с модификаторами эффекта является стратификация, которая включает в себя разделение наблюдений на страты (или подгруппы) на основе значений модифицирующей переменной. Разделив модификаторы эффекта по стратам и создав независимые ERF для каждой страты, вы можете изучить взаимосвязь между воздействием и результатом в каждой группе отдельно. Это позволит вам увидеть наличие эффекта воздейсвия на результат с разными уровнями модификатора эффекта.
Начальные доверительные интервалы
Вы можете создать 95-процентные доверительные интервалы для ERF, используя параметр Создание начальных доверительных интервалов. Созданные доверительные интервалы будут показаны пунктирными длиниями выше и ниже ERF выходном слое графики и в сообщениях. Если создается выходная таблица ERF, она также будет содержать поля для верхней и нижней границ доверительного интервала.
Доверительные интервалы представляют собой границы среднего по совокупности значения переменной результата для любого заданного значения переменной воздействия. Так как среднее по совокупности будет иметь меньшую вариабельности, чем отдельные участники совокупности, большая часть точек на диаграмме рассеяния не попадает в пределы доверительных интервалов, но это не признак проблемы. По той же причине доверительные интервалы применяются только к глобальной ERF, и не могут быт применены к какой-либо локальной ERF.
Доверительные интервалы создаются с использованием начальных значений M-out-of-N. Этот процесс предполагает случайную выборку M наблюдений из N наблюдений, где M=2*кв.корень из (N), в соответствии с рекомендациями DasGupta (2008). Затем инструмент выполняет полностью весь алгоритм (поиск оптимальных парамеров, вычисление оценок предрасположенности, тестирование баланса и вычисление ERF) для произвольной начальной выборки. Результирующая ERF обычно бывает подобна исходной ERF, но не полностью. Повторяя этот процесс несколько раз вы можете увидеть, насколько вариабельна ERF при использовании произвольных выборок наблюдений. Вариабельность результирующих ERF и определяет доверительные интервалы.
Если начальная выборка не достигает баланса (как определено типом балансировки и пороговым значением баланса), начальная выборка сбрасывается. Инструмент продолжит подбирать начальные выборки до тех пор, пока 5*кв.корень из (N) начальных выборок не достигнут баланса. Получаемое значение предполагает, что каждое наблюдение будет включено в среднем как минимум в 10 сбалансированных начальных выборок. Это позволяет получать стабильные показатели для верхней и нижней границы по всему диапазону воздействия. Если все еще не найдено сбалансированных начальных выборок после 25*кв.корень из (N) попыток, доверительный интервал не создается и возвращается предупреждающее сообщение.
Хотя доверительные интервалы охватывают большинство источников неопределенности ERF, важно понималь, что для создания доверительных интервалов, реально соответствующих верхней и нижней границам причинно-следственной связи, должны быть учтены все потенциальные источники неопределенности. Процедура поиска начальной выборки в этом инструменте включает неопределенность процедуры балансировки и оценки ERF, но она не может учитывать остальные потенциальные источники неопределенности, такие как неточность значений переменных или выбор функциональной формы ERF (взвешенное скользящее среднее, в отличие от сглаженного или глобального полиномиального, например). Кроме того, доверительные интервалы будут стремиться к максимальному сужению по мере увеличения числа наблюдений, но это не означает, что ERF является идеальной характеристикой причинно-следственной связи.
Если начальные доверительные интервалы созданы, выходные объекты или таблица будут содержать два дополнительных поля, относящихся к начальным выборкам. Первое поле будет содержать количество раз, когда наблюдение присутствует в начальной выборке, а второе поле - количество раз, когда наблюдение включено в начальную выборку, в которой выровнен баланс и получена ERF. Эти поля будут созданы, даже если не получено достаточно начальных выборок, с достижением баланса для оценки доверительных интервалов. Для выходных объектов значения в первом столбце должны показать незначительные пространственные закономерности, кроме области по периметру объектов. Тем не менее, если присутствуют пространственные закономерности во втором поле, это может указать на неучтенную пространственную закономерность. Например, если большинство сбалансированных начальных выборок относятся к определенным регионам данных, эти регионы получаются чрезмерно представлены в доверительных интервалах, и такие интервалы выходят нереалистично суженными. Если вы видите пространственные закономерности в количестве сбалансированных начальных выборок, используйте пространственные искажающие переменные (например, географический регион), чтобы учесть пропущенный пространственный эффект.
Во входных таблицах каждая начальная выборка выбирает M наблюдений случайным, неформализованным образом. Выборки допускают замещения, так что одно и то же наблюдение может быть выбрано несколько раз в одной и той же начальной выборке. Во входных векторных объектах начальные выборки создаются путем выбора случайных объектов произвольным образом, и в выборку включается как сам объект, так и его ближайшие соседи. Такая произвольная выборка выполняется несколько раз, допуская замещения, пока M наблюдений не будет включено в начальную выборку. Одни и те же объекты могут быть произвольно выбраны несколько раз, и также могут быть включены как соседи несколько раз. Использование случайных соседей, вместо полностью случайной выборки помогает скорректировать не измеряемое пространственное искажение (хотя по-прежнему рекомендуется корректировать пространственное искажение, включая пространственные переменные в качестве искажающих).
Так как ERF не могут расширяться за пределы диапазона значений воздействия, используемых для построения функций, ERF каждой начальной выборки будет создана только между минимальным и максимальным значениями воздействия для наблюдений в произвольной выборке. Это означает, что максимальное и минимальное значения воздействия часто не попадают в диапазон значений, выбранных случайным образом, поэтому для экстремумов создается меньшее количество начальных ERF.
После завершения процесса поиска начальных выборок создаются 95% доверительные интервалы, используя величину распределения Т для начальных значений ERF для каждого значения воздействия. Вариабельность значений ERF пересчитывается путем умножения (M/N) для подгонки только выбранных значений M, а степенью свободы будет число начальных ERF, которое могло быть сгенерировано для значения воздействия минус 1. Кроме того, ширина доверительных интервалов сглаживается на основе того же ядра сглаживания, который использовалось для оценки исходного ERF (равные веса с надстройкой ширины полосы). Затем сглаженная ширина добавляется и вычитается из исходной ERF для получения верхней и нижней границ доверительного интервала. Если создается выходная таблица ERF, она будет содержать поля со сглаженным среднеквадратическим отклонением (сглаженная ширина, деленная на критическое значение) и количество начальных ERF, которые могут быть сгенерированы для значения воздействия.
Список литературы
DasGupta, Anirban. 2008. "Asymptotic Theory of Statistics and Probability." Biometrics. 64: 998-998. https://doi.org/10.1111/j.1541-0420.2008.01082_16.x
Fan, Jianquin. 1996. "Local Polynomial Modeling and Its Applications: Monographs on Statistics and Applied Probability 66." (1st ed.). Routledge. https://doi.org/10.1201/9780203748725.
Imbens, Guido and Donald B. Rubin. 2015. "Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction." Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9781139025751.
Khoshnevis, Naeem, Xiao Wu, and Danielle Braun. 2023. "CausalGPS: Matching on Generalized Propensity Scores with Continuous Exposures." R package version 0.4.0. https://CRAN.R-project.org/package=CausalGPS.
Wu, Xiao, Fabrizia Mealli, Marianthi-Anna Kioumourtzoglou, Francesca Dominici, and Danielle Braun. 2022. "Matching on Generalized Propensity Scores with Continuous Exposures." Journal of the American Statistical Association. https://doi.org/10.1080/01621459.2022.2144737.