近接する観測データの値が類似しているときに、空間データは空間的自己相関を示すことがあります。 回帰モデルでこれを無視した場合、推定値に偏りが生じ、間違った推測になることがあります。
[空間的自己回帰 (Spatial Autoregression)] ツールは、空間依存を明示的に考慮した空間回帰モデルを適合させることによってこれらの課題に対応するように設計されています。 このツールは、従来の最小二乗法回帰モデルまたはいずれかのグローバル空間回帰モデル (空間ラグ モデル、空間誤差モデル、空間自己回帰結合モデル) を実行することができます。 このツールで使用するモデルを指定できます。指定しなかった場合、従属変数と説明変数に対して一連の診断検定が実行され、最も適切なモデルが特定されます。
これらの回帰モデルの目的は、空間依存の存在下で回帰モデルの確実な推測を可能にすることです。 空間回帰モデルを使用することで、推定値についての確信を持てるため、モデル内の空間の効果について推定することができます。
適用例
[空間的自己回帰 (Spatial Autoregression)] ツールを使用して、主に 2 つの方法によって、モデル内の空間依存を考慮することができます。
1 つ目の空間ラグ モデルは、次のような空間スピルオーバー効果の分析に役立ちます。
- 公衆衛生と疫学 - 空間依存を考慮して、疾病やウイルスの伝播を評価します。
- 犯罪学 - 近隣効果を加味して、犯罪の地理的な集中と分散について把握します。
2 つ目の空間誤差モデルでは、次のように、説明変数の空間依存を考慮して、偏りのないモデルの推定を行うことができます。
- 社会経済分析 - 説明変数の空間相関因子を制御して学歴を評価します。
- 住宅価格 - 資産価値に影響を与える測定不能な空間因子を制御して、主要なモデル変数についての知見を明らかにします。
モデル タイプ
[空間的自己回帰 (Spatial Autoregression)] ツールでは、それぞれ異なる方法で空間依存を考慮する 3 つのグローバル空間回帰モデルを推定できます。 各種診断に基づいて、この 3 つの空間回帰モデルのいずれも適していないことが明らかになった場合、「最小二乗法」回帰が実行されます。
空間誤差モデル
空間誤差モデル (SEM) は、回帰モデルの残差に空間的自己相関が存在する状況に対処するように設計されています。 SEM では、空間依存は局外パラメーターと見なされます。 局外パラメーターは、適切な推測が確実に行われるために考慮されなければならないものです。 SEM モデルは次の式によって定義されます。
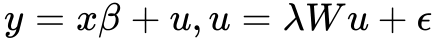
これは最小二乗法回帰の式とよく似ており、従属変数 (y) が説明変数 (x) と係数 (β) によって予測されます。 ただし、残差項 (u) は別の回帰方程式によってモデル化されます。 この 2 つ目の回帰は、空間自己回帰パラメーター λ (ラムダ)、空間加重マトリックス (W)、この回帰自体の残差項 (ε) を使用して残差を予測します。 ラムダ パラメーターは誤差項の空間依存の強度を定量化し、ある位置の誤差項がその近接フィーチャの誤差項に与える影響を表します。
SEM は、モデルの各変数から空間的自己相関をフィルターによって除外し、空間的にフィルターされた変数に対して回帰を実行します。 この結果、係数の推定値は各変数の空間的自己相関による影響を受けません。
空間ラグ モデル
空間依存を局外パラメーターと見なす SEM とは異なり、空間ラグ モデルは空間依存を説明変数として取り込みます。 空間ラグ モデルは、従属変数に強い空間的自己相関があり、空間スピルオーバー効果がある (あるエリアでの変化が近接するエリアでの変化をもたらす) 場合に使用します。 SLM モデルは次の式によって定義されます。
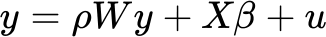
従属変数は説明変数と従属変数の空間ラグ (Wy) によって予測されます。 空間自己回帰パラメーター ρ (rho) は、ある位置の近接フィーチャが従属変数の値 (y) に与える影響の強さを表します。 ρ パラメーターの推定値が大きい場合、これは拡散プロセスであることを示唆しています。このプロセスでは、ある位置における値が近接位置における値に影響を与え、 今度は、近接フィーチャが元の位置に影響することで、フィードバック ループが生じます。
空間自己回帰結合モデル
空間自己回帰結合モデル (SAC) には、空間誤差モデルからの空間自己回帰パラメーター λ と、空間ラグ モデルからの空間自己回帰パラメーター ρ が含まれています。
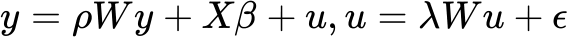
この場合、誤差項の空間依存と従属変数の空間ラグがモデル化されます。 SAC モデルを使用することで、従属変数の空間スピルオーバー効果を明らかにしながら、誤差項の空間依存にも対処することができます。
適切なモデルの選択
デフォルトでは、このツールはラグランジュの未定係数法 (LM) 検定 (Rao スコアとも呼ぶ) と呼ばれる一連の統計的検定に基づいて最も適切なモデルを選択します。 この選択プロセスは主に、Anselin と Rey (2014) によるワークフローに基づきます。
モデル選択の決定基準を次のフロー チャートに示します。
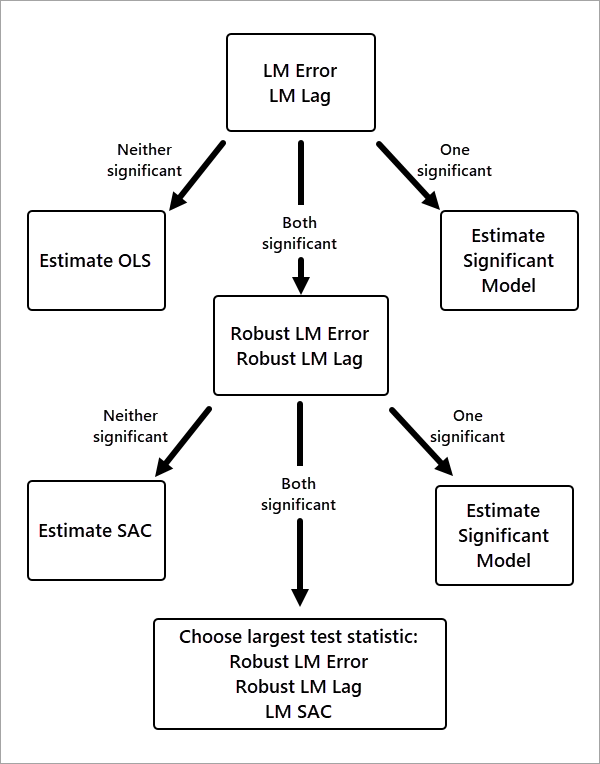
最初に、空間ラグ (LM ラグ) モデルと空間誤差 (LM 誤差) モデルについての LM 検定が実行されます。 どちらの検定も統計的に有意でない (p 値が 0.05 より大きい) 場合、空間モデルは不要であり、OLS モデルが選択されます。 いずれか一方の検定のみが有意である場合、そのモデルが選択されます。
LM ラグ検定と LM 誤差検定の両方が有意である場合、両方のロバスト LM 検定が実行されます。 ロバスト LM ラグ検定とロバスト LM 誤差検定は、少し厳密な形式の検定です。 いずれか一方の検定のみが有意である場合、そのモデルが選択されます。
両方のロバスト検定が有意である場合、SAC モデルに対して LM 検定が実行されます。 この 3 つの検定すべてが有意である場合、検定統計量が最も大きいモデルが選択されます。
まれなケースとして、LM ラグ検定と LM 誤差検定の両方が有意であるが、どちらのロバスト検定も有意でない場合、SAC モデルが選択されます。
LM 検定はデータ主導によるモデル選択のアプローチであることに注意することが重要です。 これによってモデルや適合が良好であることは保証されません。 診断を確認してモデルの理論上の仮定について検討します。
ツールの出力
このツールの主な出力は、ジオプロセシング メッセージ内の複数のテーブル、出力フィーチャクラス、モデルの残差を視覚化したチャートです。
出力フィーチャ
このツールの出力フィーチャクラスには、各フィーチャの従属変数、説明変数、従属変数の予測値、残差と標準化残差、残差の空間ラグ、隣接フィーチャの数が格納されます。
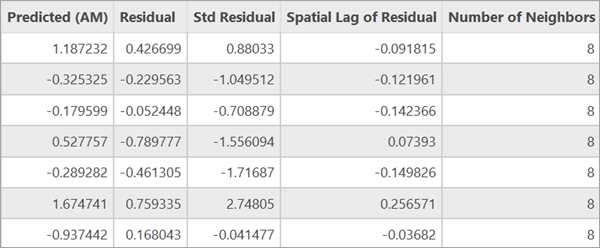
マップにレイヤーを追加すると、フィーチャの標準化残差に応じてフィーチャに濃淡が付きます。 標準化残差を視覚化することで、誤差項のクラスタリングのパターンを容易に把握できるようになります。
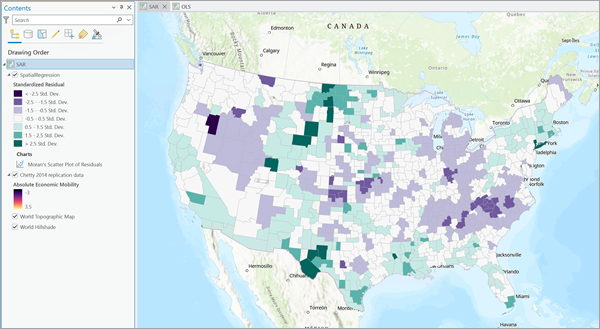
残差は濃い紫色から濃い緑色の間でシンボル表示されます。 緑色でシンボル表示された位置には正の残差があり、そのモデルでは過大な値が推定されたことを意味します。 同様に、紫色の位置には負の標準化残差があります。 負の残差は、その位置で過小な値が推定されていることを示しています。
残差の Moran 散布図
出力レイヤーには、残差とその空間ラグの関係をプロットした散布図が含まれています。 x 軸は標準化残差を示し、y 軸は標準化残差の空間ラグを示しています。 このタイプのチャートを Moran 散布図と呼びます。
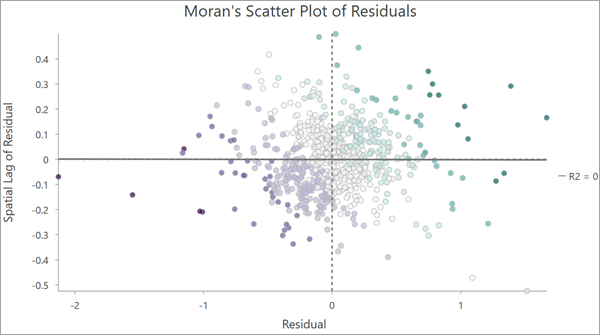
このチャートは x 軸と y 軸上の 0 を中心に 4 つの象限に分割することができます。 右上と左下の象限の値には正の空間的自己相関があります。 これらの位置では、それぞれ正の値と負の値が、その近接フィーチャとほぼ同じです。 左上と右下の象限の位置には負の空間的自己相関があります。 これらの位置では、高値が低値で囲まれています (または低値が高値で囲まれています)。
残差が 4 つの象限に均等に分布している場合、識別可能な空間的自己相関はありません。 回帰モデルの性能が良好であり、大部分の空間的自己相関が考慮された場合、このタイプのパターンとなります。
ジオプロセシング メッセージ
このツールでは、各モデルがどのように推定されたかについての情報を含む複数のテーブルがジオプロセシング メッセージとして返されます。
- 近傍および空間加重のサマリー
- LM 検定の結果
- モデル結果のサマリー
- モデル診断
場合によっては、次のメッセージ テーブルも表示されます。
- 係数効果のサマリー
- 一致ポイント レポート
以下のセクションで、各テーブルについて説明します。
近傍および空間加重のサマリー
SEM、SLM、SAC の各モデルには空間加重マトリックスが必要であり、空間加重マトリックスはモデルの結果に大きな影響を与えることがあります。 近傍および空間加重のサマリー テーブルでは、モデルの適合に使用された空間加重マトリックスについての情報が提供されます。 近傍タイプ、加重スキーム、空間接続性、平均近傍サイズ、最小近傍サイズ、最大近傍サイズが報告されます。
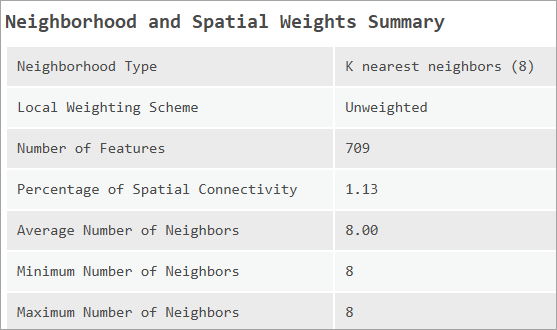
空間加重マトリックスの接続性が高すぎる場合にはモデルが推定されないことに注意することが重要です。 空間接続性の割合は、各フィーチャの近接フィーチャの概算の平均数を、フィーチャの総数に対する割合として示した値です。 たとえば、500 個のフィーチャがあり、空間接続性が 0.1 である場合、各フィーチャには平均で約 50 個の近接フィーチャがあります。 空間加重マトリックスに 30 パーセント以上の接続性がある場合、そのモデル結果に偏りが生じます (Smith, 2009)。 この場合、このツールからエラーが返されます。
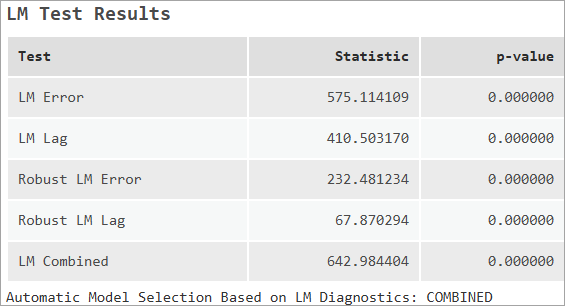
LM 検定の結果
LM 検定の結果テーブルでは、各検定でのラグランジュの未定乗数法診断が報告されます。 このテーブルには、上記の「適切なモデルの選択」セクションで示したフロー チャートに基づいて選択されたモデル タイプも表示されます。
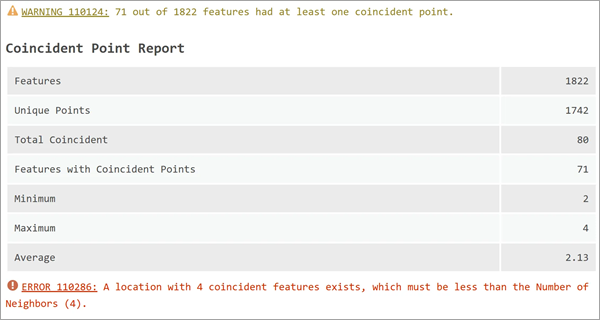
一致ポイント レポート
一致ポイント (同じ座標を持つ複数のポイント) により、すべての近接フィーチャに 0 の加重が作成されるなど、空間回帰でさまざまな問題が生じる可能性があります。 入力フィーチャに一致ポイントが存在する場合、一致ポイント レポートが表示され、フィーチャの総数、一意の位置の数、すべてのフィーチャの一致ポイントの最小数、最大数、平均数が報告されます。 さらに、一致ポイントによって生じた警告とエラーも表示されます。
モデル診断
モデル診断テーブルには、従属変数、フィーチャ数、自由度、使用されたモデルなど、重要な診断情報が表示されます。
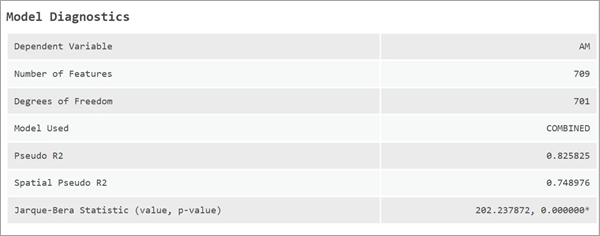
OLS モデルが推定された場合、調整済み決定係数がテーブルに表示されますが、 空間モデルの場合、代わりに擬似決定係数が表示されます。 SLM モデルと SAC モデルの場合、空間擬似決定係数も表示されます。 これについては以下で説明します。
さらに、Jarque-Bera 統計量も報告されます。 この統計量が有意である場合、そのモデルの残差は正規分布していないことを示しています。 これらのモデルは非正規性に対してロバストな手法を使用して推定されますが、モデルの誤指定や外れ値の存在が検定によって示されることがあります。
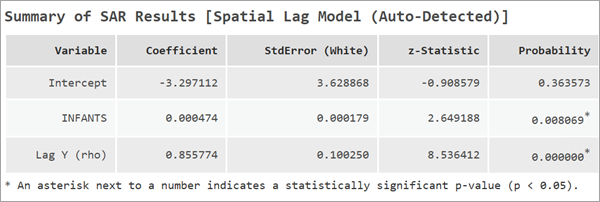
空間ラグ モデルの結果の解釈
空間ラグ モデルでは、ラグ Y (rho) と呼ばれる追加の係数が報告されます。 これは従属変数の空間ラグです。 この変数の係数は、従属変数の空間依存の強度と方向を示します。 rho の値は -1 ~ 1 の間でなければなりません。 ラグ Y の値が大きいほど、空間フィードバック プロセスが強いことを示します。
ある位置における説明変数の変化が別の位置における従属変数の値に影響を与える可能性があることに注意する必要があります (これを空間スピルオーバー効果と呼びます)。 空間スピルオーバー効果が存在する場合、空間スピルオーバー効果とともに回帰係数を解釈する必要があります。
インパクトと係数効果
回帰係数に加え、インパクトと呼ばれる指標が報告されます。 インパクトは、各説明変数の空間スピルオーバー効果を表します。 インパクトは直接インパクト、間接インパクト、総インパクトに分類されます。 インパクトの計算にはいくつかの異なるアプローチがあり、このツールでは単純インパクトが報告されます。 直接インパクト、間接インパクト、総インパクトは係数効果のサマリー メッセージ テーブルに表示されます。
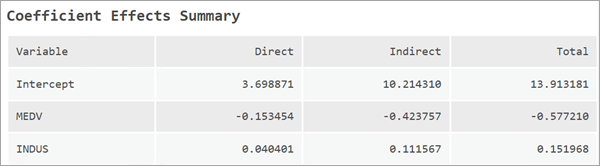
直接インパクトは、ある説明変数の 1 単位の変化がその位置自体の従属変数の値に与える影響を表します。 単純インパクトの場合、これはベータ係数と同じ値になります。
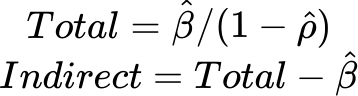
その一方で、間接インパクトは、ある変数の 1 単位の変化がそれと隣接する位置の従属変数に与える影響を表します。 ただし、インパクトの値は空間加重マトリックスから強い影響を受けることに注意してください。
標準誤差
デフォルトで、空間ラグ モデルではロバスト標準誤差が報告されます。 ただし、空間ラグ モデルを適合した後も、残差内に多くの自己相関が残る場合があります。 Anselin-Kelejian (AK) 検定は、モデルの残差に多くの空間依存が残るかどうかを判別するときに使用する診断検定です。
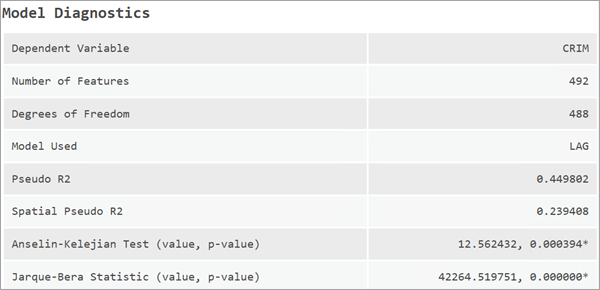
AK 検定が有意である場合 (p 値が 0.05 未満)、HAC (heteroskedastic and autocorrelation) ロバスト標準誤差と呼ばれる、標準誤差の別の指標が報告されます。 HAC 標準誤差は標準誤差の非パラメトリック バリアントであり、空間的自己相関が存在する場合に便利です。
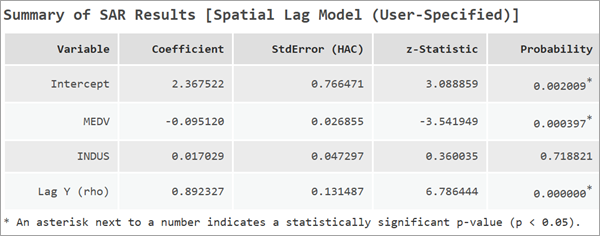
HAC 標準誤差では、別個の空間加重マトリックスを使用してデータの空間分布が考慮されています。 K 最近隣内挿法を使用して空間加重マトリックスが作成され、各フィーチャの近傍と、近傍に含まれているフォーカル フィーチャが特定されます。 各近傍の加重は三角カーネルを使用してモデル化されます。
擬似決定係数と空間擬似決定係数
空間ラグ モデルには説明変数として従属変数の空間ラグが含まれているため、従来の線形回帰予測手法は使用できません。 従属変数をその空間ラグを使用して予測すると、自信過剰な推定値になります。 これを克服するため、空間擬似決定係数と呼ばれる別の指標が計算されます。
空間擬似決定係数の計算に従属変数の空間ラグは使用されません。 代わりに、空間加重マトリックスと λ の推定値を使用して予測値 Wy-hat が作成され、これが Wy の代わりに予測で使用されます。
この予測値を使用して、従来の擬似決定係数の値が計算されます。 擬似決定係数の値ではなく空間擬似決定係数の値を報告することをおすすめします。
空間擬似決定係数は OLS の結果によって報告される調整済み決定係数とは別の指標であることに注意してください。 このため、この 2 つを比較するのは適切ではありません。
空間誤差モデルの結果の解釈
空間誤差モデルでは、標準線形回帰と同様に回帰係数を解釈することができます。 各係数は、独立変数の 1 単位の変化に対する従属変数の変化を表します。 ただし、SEM には追加のコンポーネントであるラグ残差 (ラムダ) が含まれており、これはモデル内の空間依存を理解する上で重要な役割を果たします。 ラグ残差 (ラムダ) の係数は必ず -0.99 ~ 0.99 の範囲になります。
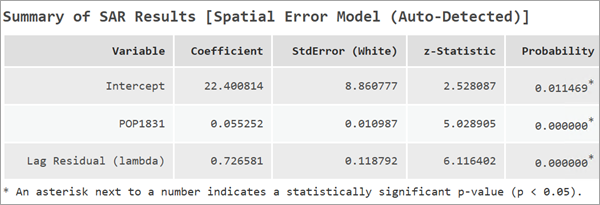
ラムダの値が正の場合、残差が空間的に集まっていることを示し、ラムダの値が負の場合、残差が空間的に分散していることを示しています。 ラムダの絶対値 (正または負) が大きい場合、説明変数によって説明されない空間プロセスが存在することも示しています。 追加の関連する説明変数を含めると、この係数がより中程度のレベルに下がることがあります。
空間自己回帰結合モデルの結果の解釈
SAC モデルが選択された場合、SLM モデルと SEM モデルに該当するすべてのセクションがメッセージに表示されます。

参考文献
このツールの実装には以下の参考文献が用いられています。
- Anselin, L., and Sergio J. Rey. 2014. "Modern spatial econometrics in practice: A guide to GeoDa, GeoDaSpace and PySAL." ISBN 9780986342103.
Bivand, Roger and Gianfranco Piras. 2015. "Comparing implementations of estimation methods for spatial econometrics." Journal of Statistical Software. 63: 1-36.「https://doi.org/10.18637/jss.v063.i18」.
Kelejian, Harry H., and Ingmar R. Prucha. 2007. "HAC estimation in a spatial framework." Journal of Econometrics. 140, no. 1: 131-154.「https://doi.org/10.1016/j.jeconom.2006.09.005」.
Smith, Tony E. 2009. "Estimation bias in spatial models with strongly connected weight matrices." Geographical Analysis. 41, no. 3: 307-332.「https://doi.org/10.1111/j.1538-4632.2009.00758.x」.