イベントまでの推定時間の動作—ArcGIS AllSource

[イベントまでの推定時間 (Estimate Time to Event)] ツールは、以前のイベントまでの時間と、オブザベーションの固有の属性に基づいて、オブザベーションのセットについてイベントが発生するまでの時間を予測します。入力は、イベントを経験したレコードと、イベントを経験していないレコードの混在している必要があります。このツールは説明変数を組み入れ、それらの変数がイベントまでの時間を短くするか、長くするかを推定します。さらに、まだイベントを経験していないオブザベーションについては、イベントが発生するまでの追加時間を予測します。

This video was created with ArcGIS Pro 3.5.

入力フィーチャまたはテーブルの各オブザベーションには、そのオブザベーションの期間を含むフィールド、イベントがすでに発生したかどうかの指標、および説明変数を含むフィールドが必要です。これらのフィールドは、それぞれ [期間フィールド]、[イベントインジケーターフィールド]、[説明変数] パラメーターで提供されます。説明変数は連続またはカテゴリで、イベントインジケーターの値は 0 (イベントが発生していない) または 1 (イベントが発生した) のどちらかのみです。期間フィールドは多くの場合、個体の実際の年齢ですが、一般にはイベントが発生した可能性がある最初の日時から開始され、イベントが発生した日時 (イベントが発生していない場合は現在の日時) で終了します。たとえば、樹木の寿命を推定するなら、期間フィールドは、樹木が現在生きているなら現在の年齢、または樹木が枯れた年齢にします。しかし、再逮捕までの時間を推定するなら、このフィールドの値は、個人が収監施設から解放した日時 (再逮捕が発生する可能性がある最初の日時) から、再逮捕の日時 (その人物が再逮捕されていなければ現在の日時) までにします。期間の単位 (時間、日、年など) を指定する必要はありませんが、すべての結果はその期間単位で解釈する必要があります。

このツールは、説明変数がイベントの日時にどのような影響を与えているかを把握するため、イベントがいつ起きるのかを予測するため、およびモデルの精度と信頼性を評価するため、数値とグラフィックスでさまざまな出力を生成します。

適用例

イベントまでの時間のモデルは、イベントが発生するまでどれだけの時間を要するのか、そしてその時間にどのような要因が影響を与えるのかを推定することが目標のさまざまな分野で有用です。このツールが応用可能ないくつかの例を、次に示します。

インフラストラクチャーの保守 - パイプラインに漏れが起きる、橋に大規模な修理が必要となる、または変圧器に障害が発生するまでの時間を推定します。説明変数として、材料のタイプ (カテゴリ)、極端な気象への曝露 (カテゴリ)、交通の負荷 (連続) などが考えられます。
山林管理 - 樹木が特定の直径に達する、伐採を必要とする、または病気で倒れるまでの時間をモデル化します。説明変数として、最初の幹径 (連続)、種 (カテゴリ)、土質 (連続)、近くの樹木との競合 (カテゴリ) などが考えられます。
クレジットデフォルト - 借り手が貸し倒れするまでの時間を予測します。説明変数として、融資額 (連続)、クレジットスコア (連続)、雇用形態 (カテゴリ)、過去の支払履歴 (カテゴリ) などが考えられます。
顧客の維持 - 顧客がサブスクリプションを解消する、またはサービスプロバイダーを乗り換える時期を予測します。説明変数として、毎月の請求額 (連続)、契約の期間 (カテゴリ)、顧客サービスへの苦情の数 (連続)、受け取られたプロモーション割引 (カテゴリ) などが考えられます。
製造 - 機械の保守や交換が必要になる時期を予測します。説明変数として、動作時間 (連続)、機械のモデル (カテゴリ)、工場の温度 (連続) などが考えられます。

イベントまでの時間の解析と生存解析

イベントまでの時間の解析は、オブザベーションのセットについてイベントがいつ起きるかを推定、説明、予測する、統計の部門です。ここでは、すべてのオブザベーションで、ある程度の時間の後でイベントが発生すると想定しています。イベントまでの時間の解析が最も広く使用されているのは医療研究です。この分野ではモデル化されるイベントが個人の死であるため、一般に生存解析と呼ばれています。この理由から、イベントまでの時間の解析では、多くの用語と概念が生存解析から借用されたものです。たとえば、オブザベーションでイベントが発生するまでの時間は寿命と呼ばれ、イベントまでの時間を推定する曲線は生存曲線と呼ばれています。樹木の死を予測する、インフラストラクチャーにいつ障害が発生するかを予測するなどの応用では、これらの用語が自然に当てはまりますが、たとえば再逮捕の時間を予測する場合などには意味が不明瞭になります。その場合、個人の生存期間は、個人が再逮捕されるまでの期間となります。同様に、個人が最低 5 年間再逮捕されない確率について語るときは、生存期間が 5 年間を超える確率と呼ばれます。このトピックでは、文脈に応じてイベントまでの時間と生存期間の話を切り替えますが、どちらも同じ内容について語っているものと理解してください。

イベントまでの時間の解析と、生存解析とのもう 1 つの違いは、生存解析は主に処置が生存期間に与える影響を推定することに特化し (通常は薬物の医療試験を行うとき)、個人の生存期間を予測することは重視していない点です。ここでの質問は基本的に、薬物によって生存期間が長くなるかであり、特定の個人がどれだけ長く生存するかではありません。しかし、イベントまでの時間の解析は、特定のオブザベーションでイベントがいつ発生するかを予測することにより特化しており、説明変数によって生存期間が増えるのか、減るのかを推定することは重視されていません。すべての生存解析モデルは、イベントまでの時間の解析に使用でき、その逆もできますが、片方に適したモデルもあります。具体的には、このツールはパラメーター的な加速された障害時間モデルを使用しており、イベントまでの時間を予測するために適しています。これに対して医療試験は一般にパラメーター的でない Cox 比例災害モデルを使用し、医療処置の効果を推定するのにより適しています。

生存曲線

イベントまでの時間を推定するときは、それぞれのオブザベーションについて、その説明変数に応じて生存曲線が作成されます。生存曲線は、生存期間が特定の期間を超える確率 (言い換えれば、個人が特定の時間後に生存している確率) をプロットする関数です。生存曲線は常に 1 から始まり、時間とともに 0 に向かって減少します。たとえば、次の生存曲線は人間の生存曲線と似たものです。

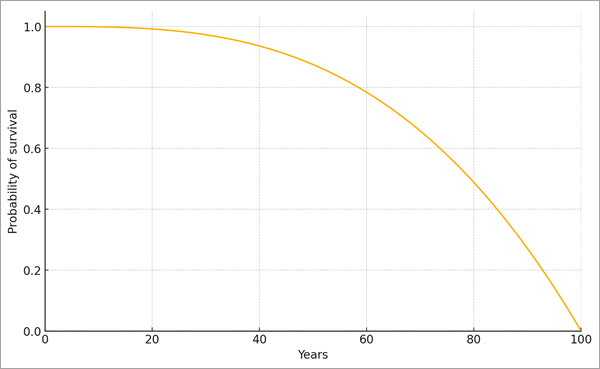
この曲線で、ほとんどの個体は 20 歳を過ぎるまで生存し、その先で比率の減少が加速しはじめます。 60 歳の時点では、80% をわずかに下回る個体が依然として生存しています。生存期間の中央値 (y 軸の 0.5) は約 80 歳で、100 歳では生存している個体はほとんどいません。

この生存曲線から、イベントまでの時間のあらゆる分位を計算できます。たとえば、イベントまでの時間の 5 パーセンタイルは、曲線が 0.95 と一致するとき (イベントがまだ発生していない確率が 95% のとき) の x 軸の値で、75 パーセンタイルは曲線が 0.25 と一致するときです。これらの分位を使用して信頼区間を作成できます。たとえば、5 パーセンタイルと 95 パーセンタイルとの間の期間は、イベントまでの時間について 90% の信頼区間となります。分位を計算できますが、多くの場合、生存曲線は生存期間の中央値 (生存曲線が 0.5 と一致するときの X 軸の値) によって集計されます。

加速された障害時間のモデル

イベントまでの時間を推定するため使用される統計モデルは、加速された障害時間 (AFT) モデルと呼ばれます。 AFT モデルは、それぞれのオブザベーションが、個別の説明変数に応じて異なる速さで老化すると想定することで動作します。たとえば、犬は人間の 7 倍の速さで老化するため、3 歳の犬は生涯において、21 歳の人間に相当する位置にいると、よく言われます (ただし、事実ではありません)。別の例として、2 つの橋は異なる速さで劣化すると考えられます。ある橋は建造から 30 年ですが、建築材料、交通量、環境条件などの橋の属性によっては、まだ 10 年しか経過していない別の橋と同程度に劣化していると見なすことができます。

AFT モデルでは、説明変数の影響によってイベントまでの時間が加速または減速され、時間比率として表現されます。 2 つのオブザベーション A と B (それぞれ説明変数が異なります) の間の時間比率は、A と B の予測される寿命の比率です。たとえば、時間比率が 1.3 なら、オブザベーション A の寿命は B よりも 30% 長いと予測されています。同様に、時間比率が 0.6 なら、40% 短いと予測されています。時間比率が 1.0 なら、どちらのオブザベーションも寿命が同じだと予測されていることを意味します。時間比率は、比較されるベースラインや基準を意味することに注意してください (この場合には、オブザベーション B の寿命)。

時間比率の効果は、生存曲線を水平方向に引き延ばすことです。たとえば、次の図に示されている 4 つの生存曲線は、時間比率が左から右にそれぞれ 1 (比較対象の青色の曲線)、2 (オレンジ色の曲線)、3 (緑色の曲線)、4 (赤色の曲線) である場合の影響を示しています。これらの曲線が互いに、他の曲線を引き延ばしたものだと認識するのは難しいため、生存期間の中央値のところに水平の破線が描かれています。時間比率 2 の生存期間の中央値は、時間比率 1 の中央値の 2 倍であることに注目してください。同様に、時間比率 3 および 4 の生存期間の中央値は、時間比率 1 の生存期間の中央値のそれぞれ 3 倍と 4 倍です。点線は中央値のところに描かれていますが、Y 軸で他のどの値を使用しても、これらの比率は維持されます。

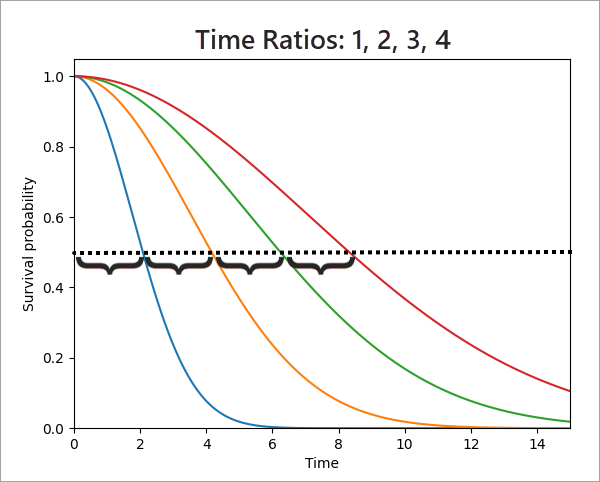
最も左にある青色の曲線をベースラインとして使用するのは恣意的な選択です。その代わりに、最も右にある赤色の曲線を比較対象のベースラインとして定義すれば、時間比率は 0.25、0.5、0.75、1 になります (左から右へ)。 1 より小さい時間比率は、4 本の曲線の中で赤色の生存曲線が、予測される生存期間が最も長いことを示しています。

このツールは、それぞれの説明変数について時間比率を推定し、時間比率の統計的な優位性をテストして、結果をメッセージで表示します (詳細については、以下の「ジオプロセシングメッセージ」セクションをご参照ください)。時間比率の解釈は、説明変数がカテゴリか連続かによって異なります。これらはそれぞれベースラインの定義方法が異なるためです。カテゴリ変数の場合、カテゴリの 1 つは参照カテゴリとして割り当てる必要があり、他のすべてのカテゴリについて、参照カテゴリと比較して時間比率が作成されます。たとえば、カテゴリ変数のフィールドに固有の値として A、B、C があり、カテゴリ A が参照カテゴリなら、時間比率はカテゴリ B と C についてのみ計算されます。カテゴリ B の時間比率が 2.2 なら、カテゴリ B のオブザベーションは、他のすべての属性が等しければ、カテゴリ A のオブザベーションよりも 2.2 倍長く生きると推定されます (これは、カテゴリ B の生存曲線はカテゴリ A の生存曲線よりも 2.2 倍幅広く引き伸ばされているというのと等価です)。このツールは、英数字順に並べ替えられた最初のカテゴリーを参照カテゴリとして使用しますが、フィールドの値を再分類すれば、参照カテゴリとして使用されるカテゴリを変更できます。

連続変数の場合、時間比率は、説明変数が 1 単位だけ増加したときの寿命の変化です。この場合、説明変数の値が正確に 1 だけ異なる 2 つのオブザベーションの間で比較が行われます (他の説明変数はすべて等しいとします)。たとえば、樹木の寿命を推定するとき、幹のメートル単位の直径が説明変数なら、時間比率は樹木の直径を 1 m だけ増やしたときの寿命の増加 (または減少) を測定します。幹の直径が大きい樹木が長生きする傾向があるなら、時間比率は 1 より大きく、寿命が短い傾向があるなら、時間比率は 1 より小さくなります。時間比率は乗数なので、説明変数が 2 単位増加すると、寿命は時間比率の 2 乗だけ増加します。説明変数が 3 単位増加すると、寿命は時間比率の 3 乗だけ増加し、以下同様です。連続の説明変数の時間比率には、このように複合的な性質があるため、モデル化が困難になることがあります (詳細とおすすめについては、以下の「ベストプラクティス、制限事項、推奨ワークフロー」をご参照ください)。

AFT モデルの推定

AFT モデルは、ワイブル分布を使用して生存曲線をモデル化します。

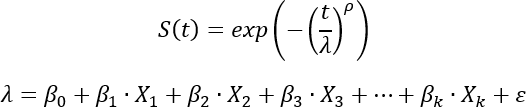
スケールパラメーター (λ) は、説明変数 (X_i) と推定される係数 (β_i) の線形モデルと推定されます。これは、前のセクションで解説したように、生存曲線の引き延ばし量をコントロールするスケールパラメーターです。直感的には、オブザベーションの特定の属性は、その属性が一般に寿命を長くするか、短くするかに応じて、そのオブザベーションの生存曲線を引き延ばし (または短縮) します。

シェープパラメーター (ρ) はすべてのオブザベーションによって共有され、生存曲線は同じ時間範囲内でさまざまな形状をとることができます。次の画像は、同じスケールパラメーターによるワイブル分布の各種の形状を示したものです。

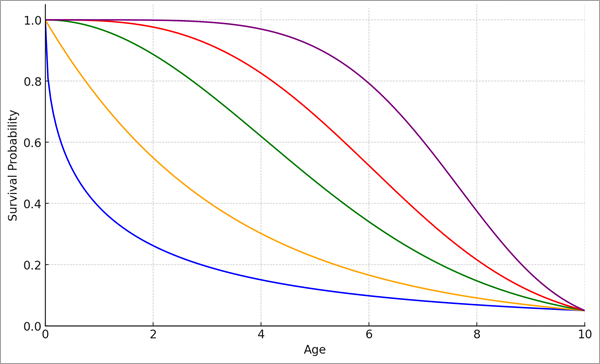
シェープパラメーターは加速パラメーターと呼ばれることもあります。これは、生存曲線が加速するか、減速するかに関連しているためです。加速はハザード関数によって測定されます。この関数は特定の日時までにイベントが発生しなかったと想定して、その日時にイベントが発生する尤度として定義されます。たとえば、古い橋が新しい橋よりも、近い将来に修理を必要とする可能性が高いなら、ハザード関数は時間とともに増加する (言い換えれば、古い橋は新しい橋よりもハザードが大きい) ため、生存曲線は時間とともに加速します。その逆に、古い橋が新しい橋よりも、近い将来に修理を必要とする可能性が低いなら、ハザード率は減少し、生存曲線は減速します。シェープパラメーターの値が 1 より大きいなら加速する生存曲線を示し、値が 1 より小さいなら減速する生存曲線を示します。しかし、ハザード率が変動し、異なる時点で生存曲線の加速と減速の両方が起きる場合、モデルは推定を行えません (たとえば、人間の寿命では乳幼児のときにハザードが大きく、子どもや若い成人はハザードが小さくなり、老人になるとハザードが再度大きくなります)。

すべての係数とシェープパラメーターは、最大の尤度を使用して推定され、ツールによりメッセージとして表示されます。

打ち切りオブザベーションと予測

これまでのセクションでは、すべてのオブザベーションについて、イベントがすでに発生したかどうかにかかわらず、生存曲線が推定されることについて説明しました。たとえば、すでに障害が発生した橋についても生存曲線を作成できます。この生存曲線は本質的に、その橋が同じ属性で今日建築されたとした場合に予測される寿命を示しています。この情報は有用かもしれませんが、まだイベントが発生していないオブザベーションの追加寿命を予測する生存曲線を作成するほうがはるかに有益です (たとえば、既存の橋が修理を必要とするまでにどれだけの期間があるかを予測します)。

イベントがまだ発生していない観測データは打ち切り観測データと呼ばれ、イベントが発生した観測データは非打ち切り観測データと呼ばれます。この用語は、非打ち切りオブザベーションには完全な情報がある (生存期間が判明しています) のに対して、打ち切りオブザベーションには部分的な情報しかない、すなわち正確な生存期間は不明で、一定期間 (オブザベーションの現在の年齢) より長いことだけが判明していることに起因しています。これは、ドキュメントが無検閲または検閲済みのいずれかであり、ドキュメントのすべての情報を使用できる可能性がある (無検閲のドキュメント) または一部が検閲によって墨消しされる可能性がある (検閲済みドキュメント) というアイデアとほぼ同じです。

打ち切りオブザベーションでは、現在の年齢を前提に、イベントまでの追加期間を推定する生存曲線を作成することが目標です。この追加の生存期間曲線は、その個体がすでに生存した期間の長さで条件付けすることにより構築できます。数学的には、追加の生存期間曲線 S_Add(T) は、SAdd_(T) = S(C+T)/S(C) で計算でき、ここで T は打ち切り時間 C 以後の追加の時間単位です。

追加の生存期間曲線は、打ち切り時間後のオブザベーションの生存曲線を再スケーリングすることで視覚化できます。たとえば下の画像は、日時 4 で打ち切られたオブザベーションの生存曲線を示すものです。説明変数に基づき、この個体が 4 時間単位以上生存する確率は約 60% でした (打ち切り日時時の Y 軸の値)。しかし、この個体が少なくとも 4 時間単位 (打ち切り日時) だけ生存したことは判明しているため、Y 軸の値は再度 1 から始まるように再スケーリングされます (言い換えると、この個体が 4 時間単位以上生存した確率は 100% です)。同様に、打ち切り日時以後の時間を測定するため、X 軸は再度 0 から開始されます。この例で、これらの説明変数を持つ個体の生存期間の中央値は約 5 時間単位 (曲線が元の Y 軸の 0.5 と交差する場所) ですが、その個体がすでに 4 時間単位生存したことが判明している場合、生存期間が約 2 時間単位 (曲線がより小さい、再スケーリングされた Y 軸の 0.5 と交差する場所) 追加され、合計の寿命は 6 時間単位になります。言い換えると、その個体がすでに 4 時間単位生存したことが判明しているなら、合計寿命の中央値は約 5 時間単位から、約 6 時間単位に増加します。オブザベーションが打ち切り前に長く生存しているほど、ベースラインの生存曲線と比較して長く生存することが予測されます。

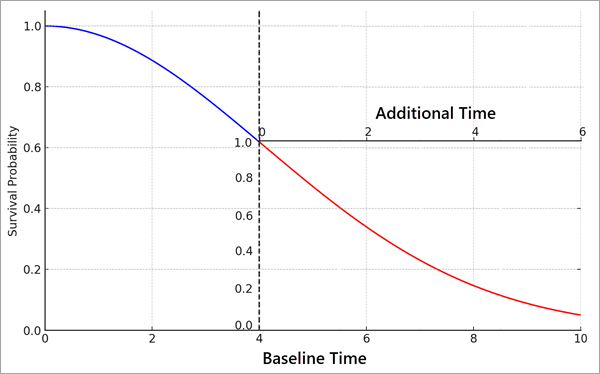
打ち切りオブザベーションでは、打ち切り後のイベントへの追加時間を示す生存曲線は、出力フィーチャまたはテーブルのポップアップチャートに表示されます。打ち切りと非打ち切りの両方のフィーチャについて、個体の生存曲線もポップアップチャートに表示されます。

打ち切り時点でのオブザベーションの年齢は、通常はオブザベーションの現在の年齢ですが、その個体が最後に観測されたとき、たとえば橋の検査が最後に行われた日時での年齢のこともあります。その場合、追加の生存期間は、オブザベーションが最後に観測されたときの年齢から始まります。

カプランマイヤー曲線

説明変数は、組み合わせごとに異なる生存曲線を生み出すため、特定のオブザベーションの寿命が標準的なオブザベーションよりも長い、または短いことが予測されるかどうかを定量化するのが困難なことがあります。オブザベーションの説明変数のいくつかは寿命を延ばし、他のものは縮めますが、全体としてオブザベーションの寿命を延ばすのか、縮めるのかは明確ではありません。個体の生存曲線に対する比較のベースとして使用できる曲線を提供するため、ツールはそのデータのカプランマイヤー曲線を計算します。

カプランマイヤー曲線は生存関数の非パラメーター的な推定で、説明変数を無視し、イベントを経験していないオブザベーションの割合の時間による変化を推定します。次の方程式を使用して、イベントと打ち切り日時をシーケンシャルに調整します。

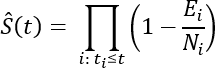
方程式で、E_i は時刻 t_i において発生したイベントの数、N_i はイベントを経験していない、または時刻 t_i より前に打ち切られたオブザベーションの数です。

この曲線は、イベントが発生するごとに減少するステップ関数として視覚化されます。この曲線は最も大きな年齢フィールドの値の時刻より先には延長できず、生存の確率は打ち切られた個体のパーセンテージより低くなることはありません。たとえば、下のカプランマイヤー曲線で、年齢フィールドの最大の値は約 3500 (X 軸の最大の値) で、オブザベーションの 40% と少しが打ち切られています (曲線の最も小さな値は 0.4 より少し大きくなります)。

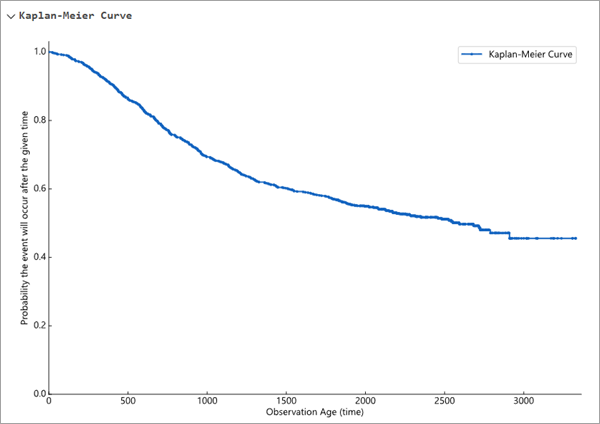
データのカプランマイヤー曲線は、ジオプロセシングメッセージの折りたたみ可能なセクションに表示されます。出力フィーチャやテーブルのポップアップチャートにも表示され、個別のオブザベーションの生存曲線と直接比較することができます (詳細については、次のセクションをご参照ください)。

ツールの出力

ツールは、結果を調査するためのさまざまな出力を返します。出力には、出力フィーチャクラスまたはテーブル、ジオプロセシングメッセージ、ポップアップチャート、ヒストグラムが含まれています。

出力フィーチャまたはテーブル

フィーチャ入力の場合、出力フィーチャレイヤーはイベントの追加時間の中央値に基づいて描画します。打ち切りフィーチャは赤色とピンク色の濃淡で描画され、濃い色ほど、イベントがすぐに発生すると予測されたことを示しています。非打ち切りのフィーチャは明るい灰色で描画され、シンボルがオーバーラップしている場合は打ち切りフィーチャの下に描画されるよう構成されています。

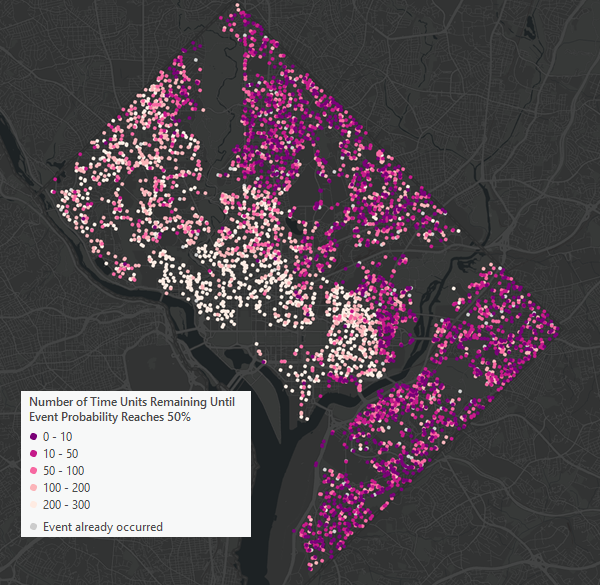
テーブルとフィーチャの両方の入力について、出力にはすべての入力フィールドのコピーとともに、イベントまでの追加時間のさまざまな分位が含まれています。フィールドには、イベントまでの追加時間の 5、10、25、中央値 (50)、75、90、95 パーセンタイルが含まれています。これらの値を使用して、イベントが発生する可能性が高い範囲を作成できます。たとえば、5 および 95 パーセンタイルを使用して 90% の信頼区間を作成できます。非打ち切りフィーチャでは、すべての分位フィールドの値に NULL 値が含まれます。イベントがすでに発生している場合、そのイベントがいつ発生するかを予測する必要がないためです。

ポップアップチャート

[生存曲線ポップアップの有効化] パラメーターがオンなら、出力のフィーチャまたはテーブルには、各オブザベーションのポップアップチャートのフィールドも含まれます。フィーチャの場合、[マップ操作] ツールを使用してマップのフィーチャをクリックすると、ポップアップチャートにアクセスできます。テーブルの場合、属性テーブルのレコードの行を右クリックすると、ポップアップチャートにアクセスできます。

非打ち切りオブザベーションの場合、ポップアップチャートにはそのフィーチャの生存曲線 (青色の曲線) が示され、青色のドットはイベント時刻を示します。これにより、オブザベーションの予測寿命から、そのオブザベーションがイベントを早く、または遅く経験したかを判別できます。モデルによって予測されるよりもはるかに早く、または遅くイベントが発生したオブザベーションについては、さらに調査することが望ましい可能性があります。カプランマイヤー曲線 (オレンジ色の曲線) も、比較のベースとしてポップアップチャートに含まれています。これによって、オブザベーションが標準的なものよりも長く生存することが予測されるか、短いことが予測されるかを判別できます。たとえば、下の画像では生存曲線がカプランマイヤー曲線よりも下側と左側にあるため、他のほとんどのオブザベーションよりも早くイベントが発生することが予測されます。青色のドットも生存曲線の中間にあり、説明変数に基づいて、イベントはモデルによって予測されるのとほぼ同じ時期に発生したことを示しています。

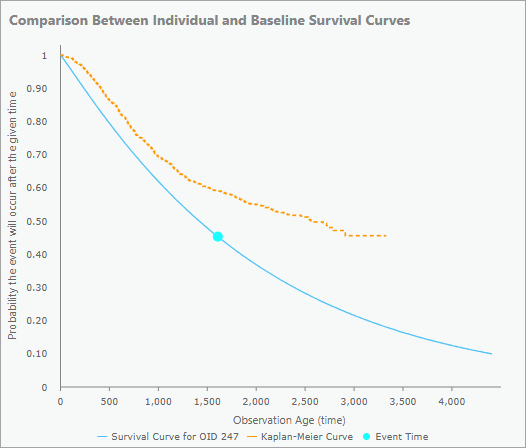
注意:

ポップアップチャートの X 軸は、生存曲線が 0.1 に達するまで延長されます (生存曲線は 0 に達しないため、カット値が必要です)。しかし、カプランマイヤー曲線は年齢フィールドの最大の値よりも延長できないため、多くの場合には生存曲線が 0.1 に達するよりも前に終了します。カプランマイヤー曲線が表示されるようにするために、X 軸は、生存曲線が 0.1 に達していなくても、カプランマイヤー曲線の長さの 2 倍よりも長く延長できません。

打ち切りフィーチャについて、ポップアップチャートにはオブザベーションの生存曲線とカプランマイヤー曲線も含まれていますが、打ち切り時刻はドットではなく青色の円で示されます。

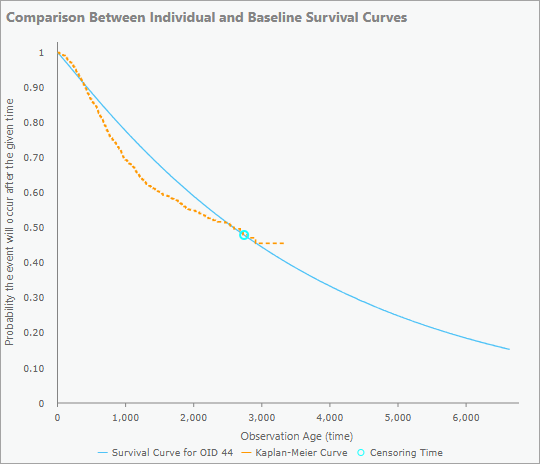
打ち切りフィーチャの場合のみ、ポップアップチャートには打ち切り後のイベントまでの追加時間のチャートも含まれます。追加時間の中央値は水平および垂直の破線として描画され、モデルでイベントが発生する確率が 50% と予測される時刻を識別します。 X 軸は、中央値が常に表示されるようにするために、生存曲線が 0.4 に達するまで延長されます。

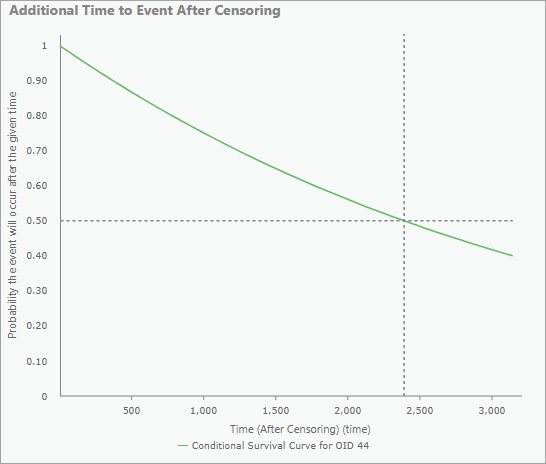
ポップアップチャートの上にポインターを置くと、曲線の特定の値を参照できます。

ジオプロセシングメッセージ

ジオプロセシングメッセージには、説明変数の影響と、モデルがデータとどの程度一致しているかについての診断結果を要約する、さまざまなセクションが含まれています。

連続説明変数

メッセージの最初のセクションには、連続説明変数の影響を要約するテーブルが含まれています。それぞれの変数について、時間比率、係数、および標準誤差 (ワイブル分布スケールパラメーターから)、係数の統計的有意性をテストする Z スコアと p 値、および時間比率の 95% 信頼区間の下限と上限がテーブルに表示されます。

末尾にはインターセプト用語の行が含まれていますが、未加工の値は一般に有意義な解釈を行えません。代わりに、インターセプトの目的は、年齢フィールドの時間単位に合わせて生存曲線をスケーリングすることです。たとえば、年齢フィールドの値を時間単位から日単位に変換すると、すべての時間比率は変化しませんが、インターセプトの時価比率は 24 で除算されます (時間数から日数への変換)。これが、ツールで年齢フィールドの単位を指定する必要がなく、単位にかかわらず同じ結果が得られる理由です。

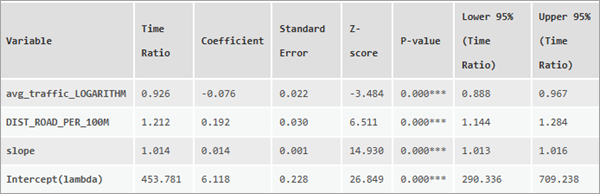
注意:

それぞれの変数について、係数とその標準誤差が AFT モデルによって直接推定され、z テストを使用して統計的有意性がテストされます。その後で、係数の指数をとることにより時間比率が計算されます: exp(coefficent)。一般に、時間比率のほうが係数よりも好まれます。これは、時間比率が未加工の生存時間と相対的に解釈されるのに対して、係数は生存時間の対数と相対的に解釈されるためです。信頼区間の上限と下限は、係数の信頼区間を作成し、端点の指数をとることで計算されます。

カテゴリ説明変数

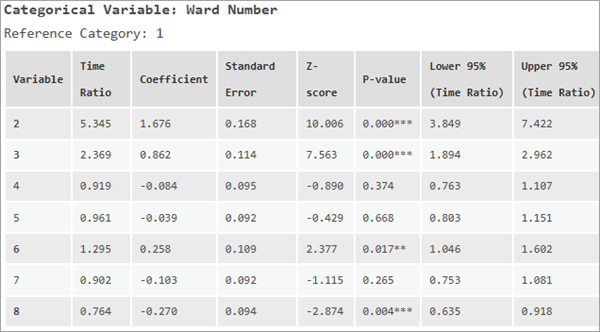
メッセージの 2 番目のセクションには、カテゴリ説明変数の影響を要約するテーブルが含まれています。それぞれのカテゴリ変数について、各カテゴリの影響を示すテーブルが表示されます。参照カテゴリはテーブルの上に表示され、すべての時間比率はそのカテゴリと相対的に解釈される必要があります。たとえば、下の画像のカテゴリ変数は区の番号で、1 区が参照カテゴリです。 2 区のオブザベーションは、1 区のオブザベーションよりも 5.345 倍だけ長く生きます (時間比率が 5.345) が、8 区のオブザベーションは 1 区のオブザベーションよりも寿命が 23.6% だけ短くなります (時間比率が 0.764)。 p 値から、4 区、5 区、7 区は 1 区と有意な差はないことも示されます。

注意:

それぞれのカテゴリ変数は一連のバイナリ (0 または 1) 変数に変換され、これらのバイナリ変数は AFT モデルの連続説明変数として使用されます。 K 個のカテゴリについて、(K-1) 個のバイナリ変数が作成され、参照カテゴリを除く各カテゴリがバイナリ変数を受け取ります (このプロセスを指標エンコーディングと呼びます)。カテゴリの 1 つを除外し、参照として使用する必要があります。これは、すべてのカテゴリのバイナリ変数を含めると、完全な共線性が発生し、モデルは係数や時間比率を推定できなくなるためです。

ワイブルシェープのパラメーター

説明変数の係数テーブルの後には、ワイブル分布のシェープパラメーターを要約するテーブルがメッセージに表示されます。このテーブルには、シェープパラメーターが統計的に 1 と異なるかどうかをテストする Z スコアと p 値も含まれています。 95% 信頼区間の上限と下限も示されます。

シェープパラメーターは、生存曲線が加速しているか、減速しているかを評価します。 1 より有意に大きい値は加速を示し、オブザベーションの年齢が高いほど、近い将来にイベントを経験する可能性が高いことを示しています。 1 より優位に小さい値は減速を示し、年齢が低いオブザベーションのほうが近い将来にイベントを経験する可能性が高いことを示しています。 1 と有意な差がない値は、オブザベーションの年齢が高くても低くても、近い将来にイベントを経験する可能性は変わらないことを示しています。このモデルは、生存曲線が常に減速または加速し続け、双方の間で切り替わることはないと想定しています。

モデルの要約統計

メッセージの最後のセクションはモデルの統計セクションで、予測の総合的な精度や、モデルの適合度に関連する統計が含まれています。このセクションには、次の統計が表示されます。

コンコーダンス指数 - 0 から 1 までの値で、ある個体が他の個体よりも寿命が長いかどうかをモデルが正しく予測する確率を示します。 1 に近い値は、どちらの個体がイベントを先に経験するかを、モデルがほぼ必ず予測できることを意味し、0.5 に近い値は、モデルによるイベントの順序の予測が、ランダムな選択と変わらないことを意味します。 0.5 よりも低い値はほとんど見られませんが、モデルによる予測がランダムな選択よりも精度が低いことを意味します。この値は、ペアリングされた個体のうち、どちらがイベントを先に経験するかをモデルが正しく予測したものの比率として計算されます。打ち切りフィーチャは生存期間が不明なため、この計算には使用されません。実践では、一般にこの値は 0.6 から 0.8 です。
AIC - AFT モデルの適合の赤池情報量基準 (AIC)。この値はほぼ情報提供ですが、たとえば高度なワークフローにおいて、説明変数の異なる組み合わせの間に、ネストした尤度比率のテストを構築するために使用できます。
p 値 - 説明変数のグローバル有意性テストの p 値。この値は、説明変数が全体としてモデルの予測を有意に改善するかどうかを示しています。この値が統計的に有意でない (一般に、0.05 よりも大きな値) 場合、モデルは説明変数が提供されないときと比べて、動作が有意に改善されません。この値は、尤度比率のテストを使用して決定されます。

逸脱残差ヒストグラム

出力フィーチャレイヤーには、オブザベーションの逸脱残差のヒストグラムも含まれています。逸脱残差は、オブザベーションがモデルで予測されるよりも寿命が長いか、短いかを定量化するという点で、他の回帰モデルの残差と概念的に似ています。正の逸脱残差は、個体が予測されるよりも寿命が長いことを意味し、負の逸脱残差は、個体の寿命が短いことを意味します (いくつかのソースでは正または負の符号が逆に定義されることに注意してください)。モデルが十分に適合していれば、逸脱残差の平均値は 0 に近くなります。

非打ち切りオブザベーションの場合、一部のものはモデルの予測より寿命が長い、または短いため、逸脱残差は正と負の両方になることがあります。しかし、打ち切りオブザベーションの逸脱残差は常に正です。この理由から、ヒストグラムはイベントインジケーターフィールドによって分割され、打ち切りオブザベーションと非打ち切りオブザベーションとでは別のヒストグラムが示されます。

逸脱残差は結果の外れ値を調べるときに最も有用で、ヒストグラムの極端な値はそれぞれ別のことを意味しています。非打ち切りオブザベーションの場合、極端な負の値は、そのオブザベーションがイベントを、モデルで予測されるよりもはるかに早く経験したことを示しており、極端な正の値は、イベントをはるかに遅く経験したことを示しています。どちらの方向にでも 3 を超える値は、外れ値、または異常なオブザベーションを示しており、さらに調査するか、データセットから取り除くことが必要な場合があります。打ち切りオブザベーションの場合、これらの値はそれほど有意義ではありませんが、一般にそのオブザベーションが打ち切られた時点で寿命のうちどれだけが経過していたかを測定しています。非常に左側の (0 に近い) 値は、そのオブザベーションが寿命の極めて早いうちに打ち切られたことを示しており、非常に右側の値は、寿命の極めて遅い時点で打ち切られたことを示しています (おそらくは、打ち切られる前ですでに、モデルの予測よりも長く生きています)。

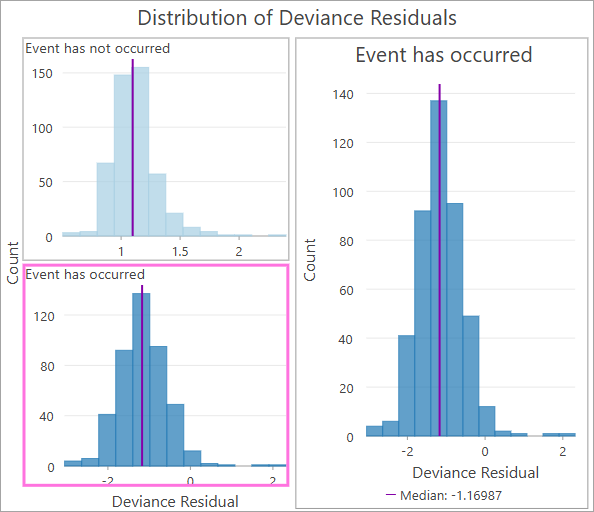
逸脱残差は次の式で計算されます。

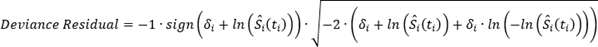
この式で、S-hat_i(t_i) は、イベントの時点 (または打ち切り時点) におけるオブザベーションの推定生存確率で、δ_i はイベントインジケーターです。

注意:

打ち切りオブザベーションの逸脱残差は常に正の値です。これは、個体がすでにある程度の時間だけ生存しているなら、ベースラインの生存曲線が予測するよりも合計寿命は長いと予測されるからです (その理由については、上の「打ち切りオブザベーションと予測」セクションの画像をご参照ください)。このプロセスにより、正しく指定されたモデルでは、逸脱残差の総合的な平均値 (打ち切りと非打ち切りの両方) が 0 になることが保証されます。

ベストプラクティス、制限、推奨のワークフロー

このツールを使用するとき、多くの制限と問題点に直面することがあります。このツールを使用するときの一般的な推奨事項とベストプラクティスを、以下に示します。

将来のいつイベントが発生するかを予測するのは本質的に困難なタスクなので、現実的な予測を維持することをおすすめします。ツールは、指定された説明変数からのみ情報を抽出しますが、インフラストラクチャーの崩壊のような複雑な減少には多数の要因が関係し、その多くはごく局所的で、それぞれの個体に固有のものです。一般に実践では、イベントまでの予測時間を、特定の日付を正確に予測するものではなく、いつイベントが発生するかを大まかに示すものと扱う必要があります。また、入力データの最大のイベント時刻よりも先まで時間を外挿するときは、特に用心し、懐疑的に扱う必要があります。イベントまでの時間の分析結果は多くの場合に不正確ですが、将来のコストの大まかな推定を行うためや、イベントを次に経験する可能性が最も高いオブザベーションを優先し、リソースを割り当てるためには非常に有用です。
イベントまでの時間のモデルは本質的に空間ではありませんが、空間情報を組み入れ、地理パターンを考慮することで、モデルが改善される場合があります。地理リージョンなどの空間の説明変数をカテゴリー説明変数として追加したり、主要なフィーチャまでの距離を連続説明変数として追加したりすることを検討します。たとえば、都市部の樹木の死亡率をモデル化するとき、最も近い建物までの距離は、建物の影による日光の減少があるため、重要な可能性があります。
モデルでは、どのオブザベーションにもある程度の時間の後でイベントが発生すると想定していますが、これが当てはまらない場合もあります。たとえば、再逮捕までの時間を予測するとき、一部の人々は決して再逮捕されませんが、モデルではそのような人々についても生存曲線を予測します。実践では、オブザベーションについて予測される追加の生存期間が非常に長いなら、イベントが永久に起きない可能性が高いことを意味しています。
連続説明変数の場合、時間比率は説明変数が 1 単位だけ増加したときに起きる、生存曲線の倍数的な変化です。しかし、一部の変数では 1 単位の変化がごく小さなもので、有意性が高く重要な説明変数についても時間比率が 1 にごく近くなる場合があります。たとえば、屋根の修理がいつ必要かを予測するとき、建物の平方メートル単位のサイズを説明変数として使用できます。しかし、建物のサイズが非常に重要であっても、面積が 1 平方メートル増えただけでは、生存曲線にごくわずかの影響しかありません。説明変数の 1 つの有意性が高い (Z スコアが高く、p 値が低い) にもかかわらず、出力された時間比率が 1.000 と等しい、または非常に近い場合、フィールドの値を大きな定数値で除算することを検討します。たとえば、平方メートルの変数を 100 で除算すると、同じ生存曲線と有意性の結果が得られますが、時間比率は建物のサイズが 100 平方メートル増加した場合の変化と解釈されるようになるため、より解釈しやすい時間比率が得られます。説明変数のいずれか (または年齢フィールド) を定数値で乗算または除算すると、同等な生存曲線が得られるため、結果の解釈に役立つようなら値を積極的に再スケーリングすることが推奨されます。
時間比率は倍数的なものなので、連続説明変数のいずれかの値が (他のデータの値と比べて) 大きいと、不安定性を引き起こしたり、生存曲線が非合理に長くまたは短くなったりすることがあります。時間比率は説明変数の 1 単位の増加に対する変化を表しており、これは指数的に計算されます。たとえば、説明変数が 5 ユニット増加すると、生存曲線は時間比率の 5 乗だけ引き延ばされます。指数変数の大きな値について、これらの指数は非常に大きくなり、生存曲線が不安定になることがあります。外れ値は特に問題となりますが、外れ値でない大きな値も生存曲線を不安定にすることがあります。これらの場合、解決策として説明変数に「対数変換」を適用します。これによって、説明変数の時間比率はさらに解釈しにくくなりますが (説明変数の対数が 1 単位増加することで、生存曲線が引き延ばされるようになります)、説明変数を対数スケールに変換すると、多くの場合に時間比率の複合効果が打ち消され、より妥当な生存曲線が得られます。
モデルのパラメーターの推定では、打ち切りと非打ち切りの両方のオブザベーションが使用されますが、非打ち切りオブザベーションは正確な生存時間が判明しているため、より多くの情報が得られます。一般に、説明変数ごとに最低 10 の非打ち切りオブザベーションがあることが推奨されます。ただし、カテゴリ変数は複数の変数としてカウントする必要があります。 2 つのカテゴリを持つカテゴリ変数は、1 つの変数とカウントします。3 つのカテゴリは 2 つの変数、4 つのカテゴリは 3 つの変数、以下同様にカウントします。さらに、カテゴリ変数のすべてのカテゴリについて影響を最適に推定するには、すべてのカテゴリごとにいくつかの非打ち切りオブザベーションが必要です。
場合によっては、オブザベーションの寿命の開始ポイントを定義するのが困難なことがあります。たとえば、橋は定期的に修理や保守が行われるため、次の修理が必要になるまでの時間を予測するとき、開始日は橋が最初に建設された日付と、橋の修理が最後に必要となった日付と、どちらも考えられます。このような場合、修理された橋が新しい橋と同等と見なせるかどうかを決定する必要があります。修理された橋が新しい橋と同等だと決定した場合、モデルの構築に役立てるため、同じ橋をデータに複数回含めることができます (修理が必要になるたびに 1 回)。しかし、修理された橋が新しい橋と同等ではないと決定した場合、橋がこれまでに修理を必要とした回数を、説明変数として使用することを試みてもかまいません。

イベントまでの時間の解析には完璧なワークフローはありませんが、モデルの構築と評価を行うため、次のような一般的なテンプレートがあります。

入力データを調査し、どの説明変数を使用するかを決定します。生存期間に関連していると判明している、または予測している説明変数を選択し、チャートでそれらの変数を調べます。説明変数と生存期間との散布図は、どの変数が生存期間と関連しているのかを判定するため特に有用です (残念ながら、これには非打ち切りオブザベーションしか使用できません)。連続説明変数の外れ値には特に注意を払い、それらを取り除くか、対数変換を適用することを検討します。カテゴリ変数については、すべてのカテゴリについていくつかの非打ち切りオブザベーションがあることを確認し、可能なら非打ち切りオブザベーションの数が少ないカテゴリは結合するか、取り除きます。
データの表現方法によっては、年齢およびイベントインジケーターのフィールドを作成するために、多くのデータエンジニアリングが必要になることがあります。たとえば、開始日と終了日のフィールドを年齢の値に変換する (このためには、[フィールド演算 (Calculate Field)] ツールの DateDiff Arcade 式を使用するのが便利です)、またはテキストフィールドをバイナリイベント指標フィールドに再分類することが必要な場合があります。
ツールを実行し、警告やエラーをレビューした後で、モデルの全体的な精度をチェックし、適合が十分でない、またはモデルの不適切な指定の兆候がないか調べます。逸脱残差のヒストグラムをレビューし、非打ち切りオブザベーションに存在する極端な逸脱の値 (正または負) には特に注意します。メッセージのモデルサマリーセクションで、p 値とコンコーダンス指数を評価し、p 値が有意でない場合は (ほとんど起きない可能性ですが) 生存期間をより適切に推定できる説明変数を探します。また、コンコーダンス指数が十分に大きく、現実的な予測を維持できるかどうかも評価する必要があります。
全体的なモデルが十分に正確なら、次にメッセージの係数テーブルをレビューし、どの説明変数が生存期間に影響しているか、そしてその影響の度合いを調べます。統計的に有意でない説明変数は取り除くことを検討します。
フィーチャの場合は、マップの出力フィーチャレイヤーを次に調査し、空間パターンを探します。一部のエリアで、他のエリアよりも生存期間が長い可能性があります。
最後に、関心のある個別のオブザベーションのポップアップチャートと属性テーブルを調査し、推定される生存曲線を確認します。

参考文献

このツールの実装には以下の参考文献が用いられています。

Collett, David. 2023. "Modelling survival data in medical research." Chapman and Hall/CRC.「https://doi.org/10.1201/9781003282525」.
Davidson-Pilon, Cameron. 2019. "lifelines: survival analysis in Python." Journal of Open Source Software. 4(40), 1317,「https://doi.org/10.21105/joss.01317」.
Klein, John P. and Melvin L. Moeschberger. 2003. "Survival Analysis: Techniques for Censored and Truncated Data." Springer Science & Business Media. ISBN 0-387-95399-X.

適用例