ブロック統計 (Block Statistics) の仕組み

[ブロック統計 (Block Statistics)] ツールは、重複しないウィンドウまたは近傍の固定セット内で入力セルの統計情報を計算する操作を実行します。 統計 (たとえば、平均値、最大値、合計値) は、各近傍に含まれるすべての入力セルに関して計算されます。 個々の近傍またはブロックについて得られた値が、指定した近傍と外接する四角形内にあるすべてのセル位置に割り当てられます。

近傍処理

概念上、セルのブロックごとに、該当するブロックで指定された近傍の形状内にある入力セルの統計情報がアルゴリズムで計算されます。 近傍は重なっていないため、特定の入力セルが 1 つのブロックの計算にのみ含まれます。

さまざまな定義済みの近傍の形状から選択できます。 カスタム形状を作成することもできます。 近傍で計算できる統計情報は、最頻値、最大値、平均値、中央値、最小値、最少頻値、範囲、標準偏差、合計値、および種類です。

概念的には、[ブロック統計 (Block Statistics)] ツールは以下のように動作します。

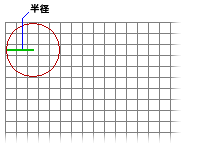
• 解析ウィンドウの左上隅に、最初に指定した近傍 (円形の近傍など) を作成します。

  

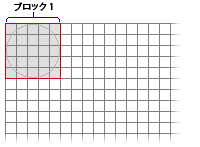
• 外接する四角形を計算して、出力ブロックのサイズを決定します。

  

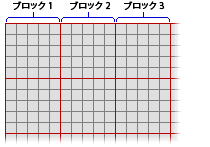
• ラスターの残りのエリアを定義済みのブロックに分割します。 ブロックは重なってはなりません。

  

• ブロックごとに、ブロック計算に使用されるセル位置を特定します。 セル位置は、四角形に接する指定の近傍 (円形の近傍など) を定義することにより決まります。

  

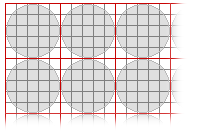
• 各ブロックの近傍ごとに出力値を計算します。 得られた値が、対応する出力ブロックの各セル位置に割り当てられます。

NoData セル

[計算時に NoData を除外] パラメーターは、近傍ウィンドウ内の NoData セルの処理方法を制御します。 このパラメーターをオンにすると (Python では ignore_nodata = "DATA")、NoData である近傍内のセルは、ブロックの出力値の計算で除外されます。 オフにすると (Python では ignore_nodata = "NODATA")、近傍内のセルが NoData の場合に、出力ブロック内のすべてのセルが NoData になります。

近傍サイズ

近傍のディメンションの最大サイズは 2,048 セルに制限されています。 つまり、四角形の近傍は、水平方向でも垂直方向でもこのセル数を超えることができません。 円形の近傍の場合は、半径が 1,023 セルを超えることができません。

近傍タイプ

近傍の形状は、ドーナツ形、円形、長方形、または扇形にできます。 カーネル ファイルを使用することで、独自の近傍の形状を定義することもでき、また、統計情報が計算される前に近傍内の特定のセルに異なる重みを割り当てることもできます。

次に、それぞれの近傍の形状とその定義について説明します。

• ドーナツ型
  • ドーナツ形の形状は 2 つの円で構成されており、ドーナツ形になるように 1 つの円がもう 1 つの円の内側にあります。 小さい円の外側および大きい円の内側に中心があるセルが近傍の処理に含められます。 2 つの円の間にある領域はドーナツ形の近傍となります。
  • 半径は、セル数、またはマップの単位で指定され、X 軸または Y 軸に垂直に計測されます。 マップ単位に半径を指定すると、それらはセル単位の半径に変換されます。 このセル単位の半径によって生成される領域は、マップ単位の元の半径で計算される領域を最もよく表しています。 ドーナツ形で囲まれるセルの中心が、近傍の処理に含められます。
  • デフォルトのドーナツ形の近傍は、内径が 1 セル、外径が 3 セルです。
  • ドーナツ形の近傍の例は、次のとおりです。

  

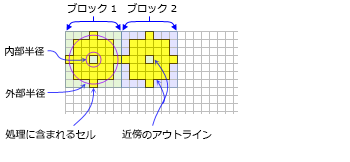
  デフォルトのドーナツ形の近傍を使用する 2 つの処理ブロックを示します (内径 1 セル、外径 3 セル)。

• 円形
  • 円の近傍は、半径の値を指定して作成します。
  • 半径は、セルまたはマップの単位で指定され、X 軸または Y 軸に垂直に計測されます。 半径がマップの単位で指定されている場合は、処理中の近傍に含まれるセルが次の方法で判定されます。 はじめに、指定した半径値で定義される円の正確なエリアが計算されます。 次に、指定した半径値が切り捨てられる円と、切り上げられる円についてエリアが計算されます。 これらの 2 つのエリアは指定した半径から得られたエリアと比較され、近い方のエリアの半径が演算に使用されます。
  • 円の近傍のデフォルトの半径は 3 セルです。
  • 円の近傍の例は、次のとおりです。

  

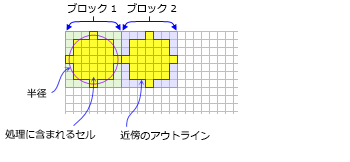
  デフォルトの円形の近傍を使用する 2 つの処理ブロックを示します (半径 3 セル)。

• 四角形
  • 四角形の近傍は、セルまたはマップ単位のいずれかに幅および高さを入力すると決まります。
  • 定義されたオブジェクト内に中心があるセルのみが、四角形の近傍の一部として処理されます。
  • 四角形のデフォルトの近傍は、高さと幅が 3 x 3 セルの正方形です。
  • 四角形の近傍の例は、次のとおりです。

  

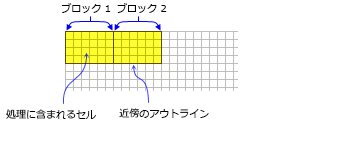
  四角形の近傍を使用する 2 つの処理ブロックを示します (幅 6 セル、高さ 4 セル)。

• 扇形
  • 扇形は、半径、開始角度、終了角度によって定義されるパイ形の近傍です。
  • 扇形の角度は、反時計回りです。 角度は、0 から 360 までの算術次数です。0 は正の X 軸 (時計の 3 時) 上にあり、整数または浮動小数で表されます。 負の角度も使用できます。
  • 半径は、セル数、またはマップの単位で指定され、X 軸または Y 軸に垂直に計測されます。 マップ単位に半径を指定すると、それはセル単位の半径に変換されます。 このセル単位の半径によって生成される領域は、マップ単位の元の半径で計算される領域を最もよく表しています。 扇形で囲まれるセルの中心が、近傍の処理に含められます。
  • 扇形のデフォルトの近傍は 0 ～ 90 度で半径は 3 セルです。
  • 扇形の近傍の例は、次のとおりです。

  

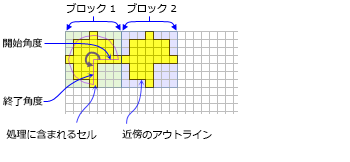
  扇形の近傍を使用する 2 つの処理ブロックを示します (半径 3 セル、始点角度 0、終点角度 270)。

• 不規則
  • 不規則な形状の近傍を指定できます。
  • 不規則な近傍を定義するカーネル ファイルで、近傍内に含めるセルの位置を指定します。
  • 以下が不規則な近傍のカーネル ファイルに適用されます。
    • このカーネル ファイルは、不規則な近傍の値と形状を定義する ASCII テキスト ファイルです。 ファイルは任意のテキスト エディターで作成できます。 このファイルには *.txt 拡張子を付ける必要があります。
    • 最初の行で、近傍の幅と高さを「X 方向のセルの数、スペース、Y 方向のセルの数」の形式で指定します。
    • 後続の行では、表される近傍内の各位置に使用する値を定義します。 それぞれの値の間にはスペースが必要です。
    • この値は、近傍内の位置を計算に含めるかどうかを定義します。 通常、不規則な近傍の計算に含める位置を特定するには値 1 を使用しますが、0 以外の任意の正または負の値を使用できます。 浮動小数の値も使用できます。
    • 近傍内のロケーションを計算から除外するには、カーネル ファイルで対応するロケーションに 0 の値 (空白ではない) を使用します。

  • 次の図は、不規則な近傍を定義する ASCII 形式のカーネル ファイルとそれが定義する近傍の例を示しています。

  

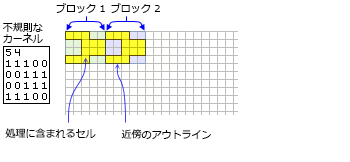
  2 つのブロックで処理するために含めるセルの図で不規則な近傍カーネルを示します。

• 加重
  • 不規則な近傍のタイプと同様に、重み付けされた近傍は不規則な近傍を定義できますが、それに加えて、入力値を重み付けできます。
  • 重みを定義するカーネル ファイルで、近傍に含めるセルの位置とそれらを乗算する重みを指定します。
  • 重み付けのある近傍は、平均値、標準偏差、および合計値の統計情報の種類でのみ使用できます。
  • 以下が重み付けのある近傍のカーネル ファイルに適用されます。
    • このカーネル ファイルは、重み付けのある近傍の値と形状を定義する ASCII テキスト ファイルです。 ファイルは任意のテキスト エディターで作成できます。 このファイルには *.txt 拡張子を付ける必要があります。
    • 最初の行で、近傍の幅と高さを「X 方向のセルの数、スペース、Y 方向のセルの数」の形式で指定します。
    • 後続の行では、表される近傍内の各位置に使用する値を定義します。 それぞれの値の間にはスペースが必要です。
    • 合計値の統計情報の場合、加重は、正または負の整数または浮動小数点で指定できます。
    • 平均値または標準偏差の統計情報の場合、加重は、正の整数または浮動小数点で指定できます。 これらの統計情報に負の値は許可されていないため、計算では負の加重が指定された位置は無視されます。
    • 近傍内のロケーションを計算から除外するには、カーネル ファイルで対応するロケーションに 0 の値 (空白ではない) を使用します。

  • 次の図は、重み付けのある近傍を定義するカーネル ファイルのコンテンツとそれが定義する近傍の例を示しています。

  

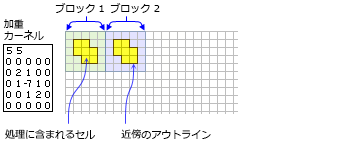
  2 つのブロックで処理するために含めるセルの図で加重近傍カーネルを示します。

統計情報の種類

使用できる統計情報は、最頻値、最大値、平均値、中央値、最小値、最少頻値、範囲、標準偏差、合計、および種類です。 統計情報のデフォルトの種類は平均値です。

• 最頻値
  • 整数ラスターのみを入力に使用できます。
  • 各ブロック近傍内の個別のセル値の頻度が求められます。 頻度が最も高い (最も頻繁に発生する) 値が 1 つである場合、その値はその近傍内のすべてのセルに割り当てられます。 同一頻度の値が複数ある場合、同一頻度の値の中で最も小さい値が割り当てられます。
• 最大
  • 入力ラスターが整数値であれば、出力ラスターの値も整数値になります。入力の値が浮動小数値であれば、出力の値も浮動小数値になります。
• 平均
  • 入力は、整数または浮動小数のラスターが使用できます。
  • 出力ラスターは常に浮動小数値になります。
  • 加重近傍タイプの場合、これはサポートされている統計情報タイプのサブセットの 1 つです。 この統計情報の計算方法の詳細については、「加重近傍」のセクションをご参照ください。
• 中央値
  • 整数ラスターのみを入力に使用できます。
  • 近傍内の有効なセル値の数が奇数であれば、値をランク付けし、中央の値を選択することで、中央値が計算されます。 近傍内の値の数が偶数の場合は、これらの値がランク付けされ、中央の 2 つの値のうち小さい方の値が選択されます。
• 最小
  • 入力ラスターが整数値であれば、出力ラスターの値も整数値になります。入力の値が浮動小数値であれば、出力の値も浮動小数値になります。
• 最少頻値
  • 整数ラスターのみを入力に使用できます。
  • 各ブロック近傍内の個別のセル値の頻度が求められます。 頻度が最も低い (発生数が最も少ない) 値が 1 つである場合、その値はその近傍内のすべてのセルに割り当てられます。 同一頻度の値が複数ある場合、同一頻度の値の中で最も小さい値が割り当てられます。
• 範囲
  • 入力ラスターが整数値であれば、出力ラスターの値も整数値になります。入力の値が浮動小数値であれば、出力の値も浮動小数値になります。
  • 次の単純な式を適用すると、出力ラスターでの各セル位置の値がセル単位で求められます。Block Range = Block Maximum – Block Minimum
• 標準偏差
  • 出力ラスターは常に浮動小数値になります。
  • 加重近傍タイプの場合、これはサポートされている統計情報タイプのサブセットの 1 つです。 この統計情報の計算方法の詳細については、「加重近傍」のセクションをご参照ください。
  • 標準偏差は、サンプルから推定される (N-1 法) のではなく、母集団全体で計算されます (N 法)。
• 合計
  • 入力ラスターが整数値であれば、出力ラスターの値も整数値になります。入力の値が浮動小数値であれば、出力の値も浮動小数値になります。
  • 加重近傍タイプの場合、これはサポートされている統計情報タイプのサブセットの 1 つです。 この統計情報の計算方法の詳細については、「加重近傍」のセクションをご参照ください。
• 種類
  • 整数ラスターのみを入力に使用できます。

加重近傍の計算

近傍内の各値が処理ブロックの最終結果に及ぼす影響の度合いは、重み付けを行うことによって調整できます。

次のセクションでは、加重平均、標準偏差、および合計の統計情報の計算に使用する式を示します。 それぞれの式に例が付属し、処理ブロックの計算と 3 x 3 セルの四角形の近傍での結果を示します。

加重平均の統計情報

重み付けのある近傍で平均値の統計情報を使用する場合、処理ブロック内のセルの出力値は、入力値を乗算したカーネル加重値の積の合計をカーネル加重値の合計で除算した値です。

近傍内のセルに適用される式は次のとおりです。

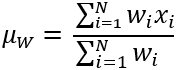
ここで、

• µ_W は処理ブロックの人口加重平均値です。
• N は近傍内のセルの数です。
• w_i はカーネルで定義された加重値です。
• x_i は入力セル値です。

レガシー:

これまでのリリースでは、分母として近傍内のセルの数が計算に使用されました。

加重値は、正の値でなければならず、整数または浮動小数のいずれかになります。

例

入力セルの次の 3 x 3 四角形ブロックについて検討してください。

4 6 7 6 7 8 4 5 6

これらの値の数学上の平均値は 53/9 = 5.889 です。

次の 3 x 3 セルの加重カーネルについて考えてみましょう。

3 3 0.0 0.5 0.0 0.5 2.0 0.5 0.0 0.5 0.0

このカーネルは、最も高い影響度をブロック内の中央のセルに付与し (重み付けが 2)、中央のセルに直交する 4 つの近傍セルの影響を緩和し (重み付けが 0.5)、4 つのコーナーのセルには影響しません (重み付けが 0)。

以下に、上記の加重平均の方程式を適用して、最終的な値を得るための計算を示します。

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) / (w1 + w2 + w3 + w4 + w5 + w6 + w7 + w8 + w9) = ((0*4)+(0.5*6)+(0*7)+(0.5*6)+(2.0*7)+(0.5*8)+(0*4)+(0.5*5)+(0*6)) / (0+0.5 + 0 + 0.5 + 2.0 + 0.5 + 0 + 0.5 + 0) = (0 + 3.0 + 0 + 3.0 + 14.0 + 4.0 + 0 + 2.5 + 0) / (0.5 + 0.5 + 2.0 + 0.5 + 0.5) = (3.0 + 3.0 + 14.0 + 4.0 + 2.5) / 4.0 = 26.5 / 4.0 = 6.625

比較すると、9 つの入力セルの通常平均値は 5.889 になります。 カーネル内にある 5 つの入力セルだけ (加重が 0 以外) を含めて、加重値を考慮しないと、平均値は 6.4 になります (6 + 6 + 7 + 8 + 5 = 32、5 で割った場合)。

加重標準偏差の統計情報

重み付けのある近傍で標準偏差の統計情報を使用する場合、処理ブロック内のセルの出力値は、次の式の結果として生成されます。

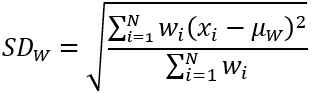
ここで、

• SDW は処理ブロックの人口加重標準偏差値です。
• µ_W は処理ブロックの人口加重平均値です。
• N は近傍内のセルの数です。
• w_i はカーネルで定義された加重値です。
• x_i は入力セル値です。

加重値は、正の値でなければならず、整数または浮動小数のいずれかになります。

近傍内のすべての入力値が同じである場合、処理ブロック内のすべてのセルの標準偏差値は 0 になります。

例

この例では、上記の加重平均の例で使用した近傍値と同じ近傍値を再び使用します。

4 6 7 6 7 8 4 5 6

同じ加重カーネル値も使用します。

3 3 0.0 0.5 0.0 0.5 2.0 0.5 0.0 0.5 0.0

上記の加重標準偏差の式をセルのブロックに適用すると、計算結果は約 0.85696 になります。 この値は、該当するブロック近傍内のすべてのセルに書き込まれます。

加重合計の統計情報

重み付けのある近傍で合計値の統計情報を使用する場合、処理ブロック内のセルの出力値は、次の式の結果として生成されます。

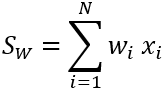
ここで、

• SW は処理ブロックの加重合計値です。
• N は近傍内のセルの数です。
• w_i はカーネルで定義された加重値です。
• x_i は入力セル値です。

加重値は、正または負のいずれかで、整数または浮動小数のいずれかになります。

例

次の近傍の入力値について考えてみましょう。

4 6 7 6 7 8 4 5 6

次の 3 x 3 セルの加重カーネルについて考えてみましょう。

3 3 -1 -2 -1 0 0 0 1 2 1

上記の式を適用した場合、最終的な値を取得するために使用される計算を次に示します。

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) = ((-1*4) + (-2*6) + (-1*7) + (0*6) + (0*7) + (0*8) + (1*4) + (2*5) + (1*6)) = (-4) + (-12) + (-7) + 4 + 10 + 6 = -3