Dans l’analyse d’adéquation, vous pouvez utiliser l’outil Correlation matrix (Matrice de corrélation) pour évaluer le mode de corrélation entre vos variables et le score final. Cette analyse identifie la multicolinéarité (variables superposées ou redondantes), qui permet une meilleure sélection des variables, des décisions de pondération plus pertinentes et une conception plus fiable de l’indice d’adéquation.
Les analyses d’adéquation comprennent souvent des variables qui mesurent des concepts similaires. Si vous ne recherchez pas les superpositions, vous risquez de compter plusieurs fois un concept et de fausser les résultats.
Exemple
Une agence publique utilise l’analyse d’adéquation pour identifier les sites potentiels d’une banque alimentaire contextuelle. Dans l’analyse, elle inclut le taux de pauvreté et le taux de chômage comme variables. Avec la matrice de corrélation, il est clair qu’il existe une forte corrélation entre le taux de pauvreté et le taux de chômage. Sans ajustement, l’analyse risque de surestimer le désavantage économique. Il est recommandé aux analystes d’envisager de supprimer une variable de la paire redondante, de fusionner les variables associées en un sous-index ou d’en ajuster les pondérations de manière à ne pas compter deux fois le même concept.
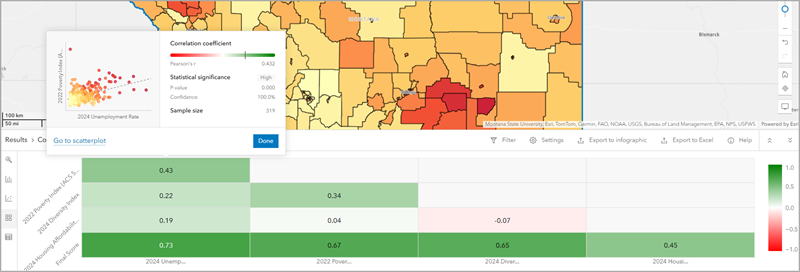
Résultats
La matrice de corrélation analyse les résultats d’une analyse d’adéquation pour valider vos choix de variables. Par exemple, vous pouvez identifier la multicolinéarité et l’influence de l’index d’équilibrage. Fort de ces connaissances, vous pouvez améliorer la force de votre analyse d’adéquation.
Pour valider vos choix de variables à l’aide de la matrice de corrélation, procédez comme suit :
- Identifiez la multicolinéarité. La multicolinéarité survient lorsque plusieurs variables ont une corrélation si forte qu’elles capturent les mêmes informations, ce qui rend difficile de distinguer l’effet individuel de chaque variable. Contrôlez les paires de variables présentant une forte corrélation (par exemple, un r de Pearson > 0,75). Pour réduire la multicolinéarité, vous pouvez envisager les solutions suivantes :
- Suppression d’une variable d’une paire fortement corrélée
- Fusion de variables corrélées en un sous-index (par exemple, vulnérabilité économique ou accès aux soins)
- Ajustement des pondérations pour limiter l’effet des variables hautement corrélées, de manière à ne pas compter deux fois le même concept
Remarque :
Application systématique des connaissances du domaine lors de la modification des pondérations.
Influence de l’index d’équilibrage. Signalez toute variable présentant une forte corrélation avec le score final (par exemple : r de Pearson > 0,85). Ajustez sa pondération ou regroupez-la avec les variables associées dans un sous-index pour éviter qu’un facteur unique ne domine le modèle. Pour une aide détaillée sur la génération de sous-index, reportez-vous à la rubrique Créer des indices composites à l’aide d’ArcGIS.
Calculs
L’analyse d’adéquation effectue les calculs à l’aide des variables sélectionnées ; elle inclut souvent des variables conceptuellement ou statistiquement similaires. Si vous ne recherchez pas les superpositions, vous risquez d’inclure à tort plusieurs variables représentant le même concept sous-jacent et d’obtenir des résultats biaisés ou faussés.
Coefficient de corrélation
Le coefficient r de Pearson est compris entre -1 à 1 et mesure à la fois la direction et la force d’une relation linéaire. Par exemple, les valeurs plus proches de +1 indiquent une forte relation positive tandis que les valeurs plus proches de -1 indiquent une forte relation négative. Les valeurs proches de 0 indiquent une relation linéaire faible ou nulle. Dans la matrice de corrélation, vous pouvez filtrer la visualisation en fonction de la valeur r de Pearson.
Signification statistique
La signification statistique indique la probabilité qu’une corrélation soit réelle et non juste le fruit du hasard. Les valeurs p faibles (par exemple, p < 0,01) indiquent une relation plus fiable statistiquement, ce qui signifie que la corrélation est moins probablement le fruit du hasard. Dans la plupart des cas, une valeur p inférieure à 0,05 est considérée significative d’un point de vue statistique. Une valeur p de 0,05 correspond à un niveau de confiance de 95 pour cent et représente un seuil courant pour déterminer la signification statistique.
Dans la matrice de corrélation, vous pouvez filtrer la visualisation en fonction de la signification statistique des variables. Des astérisques sont utilisés pour représenter la signification statistique, comme suit :
| Astérisques | valeur de p | Signification statistique |
|---|---|---|
*** | p < 0,001 | Très significatif |
** | p < 0,01 | Modérément significatif |
* | p < 0,05 | Significant (Significatif) |
Aucun | Aucun | Pas significatif statistiquement |
Limitations
La matrice de corrélation n’est disponible que dans le processus d’analyse d’adéquation.
Crédits
Ce processus consomme des crédits. L’exportation des résultats dans Excel coûte environ 10 crédits par millier d’enregistrements.
Pour plus d’informations sur la consommation de crédits, reportez-vous à la table Crédits dans Business Analyst Web App.
Licences requises
Le processus d’analyse d’adéquation est accessible aux utilisateurs disposant d’une licence Advanced pour Business Analyst Web App. Pour en savoir plus sur les types de licence Business Analyst, reportez-vous à la rubrique Licences.
Ressources
Pour en savoir plus sur l’analyse d’adéquation, consultez les ressources suivantes :
Vous avez un commentaire à formuler concernant cette rubrique ?