L’outil Courbure permet de calculer la seconde valeur dérivée de la surface en entrée cellule par cellule.
Remarque :
L’outil Courbure ajuste un plan aux neuf cellules locales, mais un plan peut ne pas être un bon descripteur de paysage et est susceptible de masquer ou d’exagérer les variations naturelles qui vous intéressent. L’outil Paramètres de surface ajuste une surface au voisinage des cellules et non un plan, l’ajustement au terrain étant alors plus naturel.
L’outil Courbure utilise une fenêtre de cellules de 3 par 3 pour calculer la valeur, tandis que l’outil Paramètres de surface autorise des tailles de fenêtre allant de 3 cellules par 3 à 15 cellules par 15. Les tailles de fenêtre plus grandes sont utiles avec des données d’élévation haute résolution pour capturer les traitements de surface au sol à une échelle appropriée. L’outil Paramètres de surface offre également une option de fenêtre adaptative qui évalue la variabilité locale du terrain et identifie la taille de voisinage appropriée la plus grande pour chaque cellule. Cela peut s’avérer utile dans le cas d’un terrain graduellement homogène interrompu par des cours d’eau, des routes ou des ruptures nettes de la pente.
L’outil Paramètres de surface inclut trois types de courbure qui utilisent des formules mises à jour et créent des résultats différents de ceux obtenus avec l’outil Courbure.
Pour chaque cellule, une fonction polynomiale du quatrième degré sous la forme suivante :
Z = Ax²y² + Bx²y + Cxy² + Dx² + Ey² + Fxy + Gx + Hy + ILa relation entre les coefficients et les neuf valeurs d’altitude pour chacune des cellules numérotées comme sur le diagramme, est la suivante :
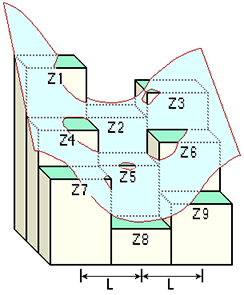
A = [(Z1 + Z3 + Z7 + Z9) / 4 - (Z2 + Z4 + Z6 + Z8) / 2 + Z5] / L4 B = [(Z1 + Z3 - Z7 - Z9) /4 - (Z2 - Z8) /2] / L3 C = [(-Z1 + Z3 - Z7 + Z9) /4 + (Z4 - Z6)] /2] / L3 D = [(Z4 + Z6) /2 - Z5] / L2 E = [(Z2 + Z8) /2 - Z5] / L2 F = (-Z1 + Z3 + Z7 - Z9) / 4L2 G = (-Z4 + Z6) / 2L H = (Z2 - Z8) / 2L I = Z5La sortie de l’outil Courbure est la somme des dérivées secondes de la surface.
Courbure standard = -100 * ([d2z/dx2] + [d2z/dy2])La courbure est parfois décrite de manière ambiguë comme la dérivée seconde de la surface ou “pente de la pente”. Cette terminologie fait référence à la courbure longitudinale.
Courbure longitudinale = -2(D + E) * 100D’un point de vue pratique, la sortie générée par cet outil permet de décrire les caractéristiques physiques d’un bassin de drainage afin de comprendre les processus d’érosion et d’écoulement. La pente a une incidence sur les mouvements de masse descendants. L’exposition définit la direction de l’écoulement (flux). La courbure longitudinale affecte l'accélération et la décélération du flux, ce qui influence l'érosion et le dépôt. La courbure planiforme influence la convergence et la divergence du flux.
Interprétation des résultats de l’outil Courbure
L’affichage des isolignes sur un raster peut vous aider à comprendre et interpréter les données résultant de l’exécution de cet outil. Vous trouverez ci-après un exemple de la procédure à suivre avec les outils identifiés et les paramètres utilisés.
- Créez un raster de courbure à partir du raster de surface avec l’outil Courbure :
Input raster (Raster en entrée) : elev_ras
Output curvature raster (Raster de courbure en sortie) : curv_ras
Z factor (Facteur Z) : 1
Output profile curve raster (Raster de courbure longitudinale en sortie) : profile_ras
Output plan curve raster (Raster de courbure transversale en sortie) : plan_ras
- Créez les isolignes du raster de surface avec l’outil Isoligne:
Input raster (Raster en entrée) : elev_ras
Output polyline features (Entités polylignes en sortie) : cont_lines
Contour interval (Intervalle des isolignes) : 100
Base contour (Isoligne de base) : ""
Z factor (Facteur Z) : 1
- Créez un raster de pente à partir du raster de surface avec l’outil Pente :
Input raster (Raster en entrée) : elev_ras
Output raster (Raster en sortie) : slope_ras
Output measurement (Mesure en sortie) : DEGREE
Z factor (Facteur Z) : 1
- Ensuite, créez les isolignes du raster de pente avec l’outil Isoligne:
Input raster (Raster en entrée) : slope_ras
Output polyline features (Entités polylignes en sortie) : cont_slope
Contour interval (Intervalle des isolignes) : 5
Base contour (Isoligne de base) : ""
Z factor (Facteur Z) : 1
Ajoutez le raster de courbure en tant que couche à l’affichage cartographique. Superposez les deux jeux de données d’entité isoligne que vous venez de créer et appliquez-leur une symbologie de couleurs différente.
Puis-je utiliser l’outil Paramètres de surface ?
Si la valeur du paramètre Raster en entrée est en haute résolution avec une taille de cellule inférieure à quelques mètres ou si elle inclut beaucoup de bruit, envisagez d’utiliser l’outil Paramètres de surface et l’option de distance du voisinage définie par l’utilisateur plutôt que le voisinage immédiat 3 par 3 de cet outil. L’utilisation d’un voisinage plus grand peut minimiser l’effet de surfaces bruyantes. Elle contribue également à mieux représenter les reliefs et les caractéristiques de la surface lors de l’utilisation de surfaces de haute résolution.
Bibliographie
Moore, I. D., I. D., R. B. Grayson et A. R. Landson. 1991. Digital Terrain Modelling: A Review of Hydrological, Geomorphological, and Biological Applications. Hydrological Processes 5: 3–30.
Zeverbergen, L. W., and C. R. Thorne. 1987. Quantitative Analysis of Land Surface Topography. Earth Surface Processes and Landforms 12: 47–56.
Rubriques connexes
Vous avez un commentaire à formuler concernant cette rubrique ?