Fonctionnement de l’outil Spatial Autoregression (Auto-régression spatiale)

Les données spatiales présentent souvent une auto-corrélation spatiale, dans laquelle les observations à proximité possèdent des valeurs similaires. L’ignorer dans les modèles de régression peut conduire à des estimations biaisées et des inférences incorrectes.

L’outil Spatial Autoregression (Auto-régression spatiale) est conçu pour relever ces défis en ajustant un modèle de régression spatiale qui prend explicitement en compte la dépendance spatiale. Cet outil peut effectuer une régression traditionnelle par les moindres carrés ordinaires ou utiliser l’un des modèles de régression spatiale globaux suivants : le modèle de décalage spatial, le modèle d’erreur spatiale ou le modèle combiné d’auto-régression spatiale. Vous pouvez spécifier le modèle à utiliser par l’outil ou ce dernier peut déterminer le modèle le plus approprié en effectuant une série de tests de diagnostic sur les variables dépendantes et explicatives.

Ces modèles de régression ont pour objectif de permettre l’inférence robuste des modèles de régression en présence de dépendance spatiale. Les modèles de régression spatiale améliorent la fiabilité des estimations et fournissent des estimations des effets spaciaux dans vos modèles.

Applications possibles

L’outil Spatial Autoregression (Auto-régression spatiale) peut être utilisé pour prendre en compte la dépendance spatiale dans les modèles de deux manières principales.

En premier lieu, le modèle de décalage spatial est précieux pour analyser les effets de débordement spatial, comme les suivants :

• Santé publique et épidémiologie : évaluez la propagation des maladies ou des virus en prenant en compte la dépendance spatiale.
• Criminologie : découvrez comment les crimes se concentrent et s’étendent géographiquement, en incorporant les effets de voisinage.

En second lieu, le modèle d’erreur spatiale peut fournir des estimations de modèle non biaisées en prenant en compte la dépendance spatiale dans les variables explicatives, comme les suivantes :

• Analyse socio-économique : évaluez le niveau d’éducation tout en contrôlant les facteurs corrélés spatialement dans les variables explicatives.
• Prix de l’immobilier : contrôlez les facteurs spatiaux non mesurés qui affectent les valeurs des propriétés, en expliquant mieux les principales variables des modèles.

Types de modèle

L’outil Spatial Autoregression (Auto-régression spatiale) peut estimer trois modèles de régression spatiale globaux possibles, chacun prenant en compte la dépendance spatiale de manière différente. La régression par les Moindres carrés ordinaires est effectuée si aucun des trois modèles de régression spatiale n’est considéré comme approprié d’après les divers diagnostics.

Modèle d’erreur spatiale

Le modèle d’erreur spatiale (SEM) est conçu pour traiter les cas où il existe une auto-corrélation spatiale dans les valeurs résiduelles d’un modèle de régression. Pour le modèle SEM, la dépendance spatiale est considérée comme un paramètre de nuisance. Un paramètre de nuisance est un paramètre qui doit être pris en compte pour garantir des inférences appropriées. Le modèle SEM est défini par la formule suivante :

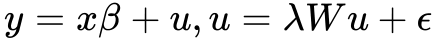
Elle est similaire à la formule de régression par les moindres carrés ordinaires, dans laquelle une variable dépendante (y) est prédite par un ensemble de variable explicative (x) et de coefficients (β). Toutefois, le terme résiduel (u) est modélisé par une autre équation de régression. Cette deuxième régression predit la valeur résiduelle à l’aide d’un paramètre d’auto-régression spatiale λ (lambda) et d’une matrice de pondérations spatiales (W), avec son propre terme résiduel (ε). Le paramètre lambda quantifie la force de la dépendance spatiale dans le terme d’erreur et indique dans quelle mesure le terme d’erreur d’une localisation influence les termes d’erreur de ses voisines.

Le modèle SEM fonctionne en éliminant l’auto-corrélation spatiale de chacune des variables du modèle et en effectuant une régression sur les variables filtrées spatialement. Par conséquent, les estimations des coefficients ne sont pas affectées par l’auto-corrélation spatiale dans chaque variable.

Modèle de décalage spatial

Contrairement au modèle SEM, qui considère la dépendance spatiale comme une nuisance, le modèle de décalage spatial (SLM) incorpore la dépendance spatiale comme une variable explicative. Le modèle de décalage spatial est utilisé si l’auto-corrélation spatiale de la variable dépendante est forte et que cette variable présente un effet de débordement spatial (les changements dans une zone entraînent des changements dans les zones voisines). Le modèle SLM est défini par l’équation suivante :

La variable dépendante est prédite par les variables explicatives, ainsi que son propre décalage spatial (W_y). Le paramètre d’auto-régression spatiale ρ (rho) mesure la force de l’influence des voisins d’une localisation sur la valeur de la variable dépendante (y). Des valeurs estimées supérieures du paramètre ρ suggèrent un processus de diffusion dans lequel les valeurs à une localisation affectent celles aux localisations voisines. À leur tour, les voisins peuvent affecter la localisation d’origine et générer une boucle de rétroaction.

Modèle combiné d’auto-régression spatiale

Le modèle combiné d’auto-régression spatiale (SAC) inclut les paramètres d’auto-régression spatiale λ et ρ des modèles d’erreur spatiale et de décalage spatial, respectivement.

Dans ce cas, la dépendance spatiale du terme d’erreur, ainsi que celle du décalage spatial de la variable dépendance sont modélisées. Le modèle SAC permet d’identifier les effets du débordement spatial dans la variable dépendante tout en résolvant la dépendance spatiale dans le terme d’erreur.

Choix du modèle approprié

Par défaut, l’outil sélectionne le modèle le plus approprié en fonction d’une série de tests statistiques appelée test LM (Lagrange Multiplier) ou score de Rao. Le processus de sélection repose principalement sur le processus décrit par Anselin et Rey (2014).

Les critères de décision permettant de sélectionner le modèle sont affichés dans l’organigramme suivant :

L’organigramme commence par le test LM des modèles de décalage spatial (LM Lag [Décalage LM]) et d’erreur spatiale (LM Error [Erreur LM]). Si aucun de ces tests n’est statistiquement significatif (valeur p supérieure à 0,05), un modèle spatial n’est pas nécessaire et un modèle OLS est sélectionné. Si un seul des tests est significatif, le modèle correspondant est sélectionné.

Si les tests LM Lag (Décalage LM) et LM Error (Erreur LM) sont tous deux significatifs, leurs contreparties robustes sont effectuées. Il s’agit des tests Robust LM Lag (Décalage LM robuste) et Robust LM Error (Erreur LM robuste) ; des formes légèrement plus strictes du test. Si un seul des tests est significatif, le modèle correspondant est sélectionné.

Si les deux tests robustes sont significatifs, un test LM est effectué pour le modèle SAC. Si les trois tests sont significatifs, le modèle dont la statistique de test est la plus élevée est sélectionné.

Dans le cas assez rare où les deux tests LM Lag (Décalage LM) et LM Error (Erreur LM) sont significatifs, mais qu’aucun des tests robustes ne l’est, le modèle SAC est sélectionné.

Notez bien que les tests LM représentent une approche dynamique du choix d’un modèle. Ils ne garantissent aucunement un modèle approprié ou un ajustement correct. Examinez les diagnostics et étudiez les hypothèses théoriques du modèle.

Sorties de l’outil

La sortie principale de l’outil est un nombre de tableaux dans les messages de géotraitement, ainsi qu’une classe d’entités en sortie et un diagramme permettant de visualiser les valeurs résidentielles du modèle.

Entités en sortie

La classe d’entités en sortie de l’outil contient les champs de la variable dépendante, des variables explicatives, la valeur prédite de la variable dépendante, la valeur résiduelle et la valeur résiduelle standardisée, le décalage spatial de la valeur résiduelle et le nombre de voisins de chaque entités.

Si la couche est ajoutée à une carte, les entités sont ombrées par leurs valeurs résiduelles standardisées. La visualisation des valeurs résiduelles standardisées peut aider à identifier d’éventuels motifs d’agrégation dans le terme d’erreur.

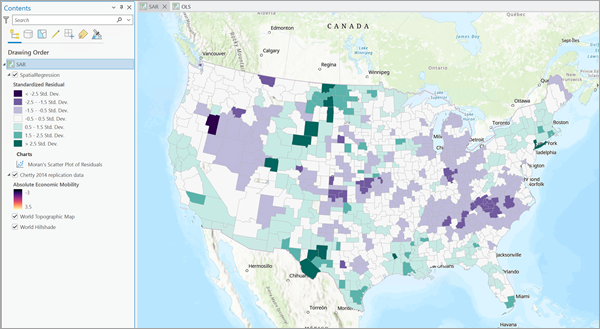
Les valeurs résiduelles sont symbolisées de violet foncé à vert foncé. Les localisations symbolisées en vert possèdent une valeur résiduelle positive, ce qui signifie que le modèle a surestimé la valeur. De même, les localisations de couleur violette possèdent une valeur résiduelle standardisée négative. Les valeurs résiduelles négatives indiquent une localisation sous-estimée.

Nuage de points de Moran des valeurs résiduelles

La couche en sortie contient un diagramme en nuage de points qui représente les valeurs résiduelles par rapport à leur décalage spatial. L’axe des x représente la valeur résiduelle standardisée et l’axe des y, le décalage spatial de la valeur résiduelle standardisée. Ce type de diagramme est appelé Nuage de points de Moran.

Ce diagramme peut être divisé en quatre quadrants autour de 0 sur les axes des x et des y. Les valeurs situées dans les quadrants supérieur droit et inférieur gauche présentent une auto-corrélation spatiale positive. Il s’agit de localisations qui contiennent des valeurs similaires à celles de leurs voisines : des valeurs positives et négatives respectivement. Les quadrants supérieur gauche et inférieur droit sont des localisations qui présentent une auto-corrélation spatiale négative. Il s’agit de localisations qui contiennent des valeurs élevées entourées de valeurs faibles (et vice versa).

Si les valeurs résiduelles sont distribuées équitablement entre les quatre quadrants, aucune auto-corrélation spatiale n’est perceptible. Ce type de motif est attendu si le modèle de régression a bien fonctionné et que la majorité de l’auto-corrélation spatiale a été prise en compte.

Messages de géotraitement

L’outil fournit un certain nombre de tables dans les messages de géotraitement, qui illustrent le mode d’estimation de chaque modèle :

• Synthèse des pondérations spatiales et du voisinage
• Résultats des tests LM
• Récapitulatif des résultats du modèle
• Diagnostics de modèle

Dans certains cas, les tableaux de messages suivants sont également affichés :

• Synthèse des effets du coefficient
• Rapport sur les points coïncidents

Chaque tableau est décrit dans les sections ci-après.

Synthèse des pondérations spatiales et du voisinage

Les modèles SEM, SLM et SAC requièrent une matrice de pondérations spatiales, qui peut en influencer fortement les résultats. Le tableau de synthèse des pondérations spatiales et du voisinage fournit des informations sur la matrice de pondérations spatiales utilisée pour ajuster le modèle. Il indique le type de voisinage, la structure de pondération, la connectivité spatiale, la taille de voisinage moyenne, la taille de voisinage minimale et la taille de voisinage maximale.

Notez que l’outil n’estime pas un modèle si la matrice de pondérations spatiales est trop connectée. Le pourcentage de connectivité spatiale correspond approximativement au nombre moyen de voisins pour chaque entité, en pourcentage du nombre total d’entités. Par exemple, avec 500 entités et une connectivité spatiale égale à 0,1, chaque entité a environ 50 voisins en moyenne. Si la matrice de pondérations spatiales possède une connectivité supérieure ou égale à 30 %, les résultats du modèle deviennent biaisés (Smith, 2009). Dans ce cas, l’outil renvoie une erreur.

Résultats des tests LM

Le tableau LM Test Results (Résultats des tests LM) contient les diagnostics LM (Lagrange Multiplier) de chacun des tests. Ce tableau affiche également le type de modèle sélectionné à partir de l’organigramme dans la section Choix du modèle approprié ci-avant.

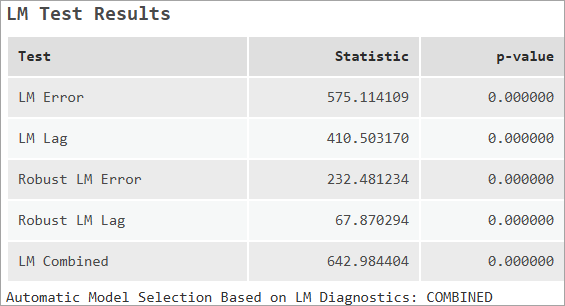
Rapport sur les points coïncidents

Les points coïncidents (points de mêmes coordonnées) peuvent provoquer divers problèmes dans la régression spatiale et notamment créer des pondérations égales à zéro pour tous les voisins. Si des points coïncidents sont présents dans vos entités en entrée, un Coincident Point Report (Rapport sur les points coïncidents) est affiché et indique le nombre total d’entités, le nombre de localisations uniques, ainsi que les nombres minimum, maximum et moyen de points coïncidents pour toutes les entités. En outre, les avertissements et erreurs générés par les points coïncidents peuvent être affichés.

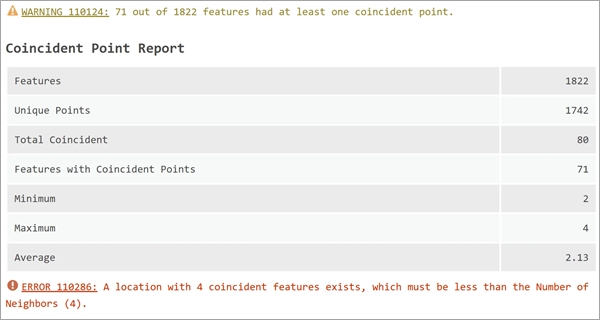
Diagnostics de modèle

Le tableau Model Diagnostics (Diagnostics de modèle) affiche des diagnostics importants, comme la variable dépendante, le nombre d’entités, les degrés de liberté, ainsi que le modèle utilisé.

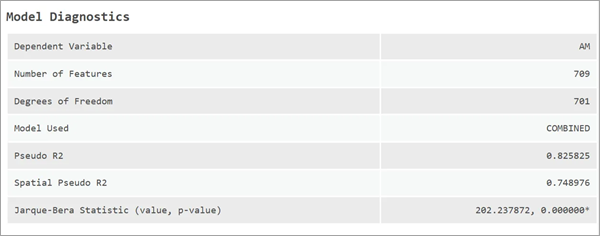
Si un modèle OLS est estimé, le R-carré ajusté est affiché dans le tableau. Toutefois, pour tous les modèles spatiaux, un pseudo R-carré est affiché à la place. Pour les modèles SLM et SAC, un pseudo R-carré spatial est également affiché. Ils sont abordés ci-après.

En outre, la statistique Jarque-Bera est également indiquée. Si cette statistique est significative, elle indique que les valeurs résiduelles du modèle ne sont pas distribuées normalement. Les modèles sont estimés à l’aide de méthodes résistant à la non-normalité, mais le test peut indiquer une spécification de modèle erronée ou la présence de points aberrants.

Interpréter les résultats du modèle de décalage spatial

Le modèle de décalage spatial renvoie un coefficient supplémentaire appelé Lag Y (Décalage Y) (rho). Il s’agit du décalage spatial de la variable dépendante. Le coefficient de cette variable mesure la force et le sens de la dépendance spatiale de la variable dépendante. La valeur de rho doit être comprise entre -1 et 1. Les valeurs de Lag Y (Décalage Y) supérieures suggèrent un fort processus de rétroaction spatiale.

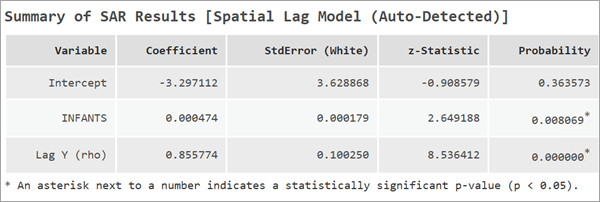
Notez qu’un changement dans une variable explicative dans une localisation peut affecter la valeur de la variable dépendante dans une autre localisation (on parle alors de débordement spatial). En présence de débordement spatial, les coefficients de régression doivent être interprétés avec l’effet de débordement spatial.

Impacts et effets des coefficients

En plus des coefficients de régression, une mesure appelée impacts est renvoyée. Les impacts permettent de mesurer l’effet des débordements spatiaux de chaque variable explicative. Ils sont divisés en impacts directs, indirects et totaux. Différentes approches permettent de calculer les impacts. Cet outil renvoie des impacts simples. Les impacts directs, indirects et totaux sont affichés dans le tableau des messages Coefficient Effects Summary (Synthèse des effets du coefficient).

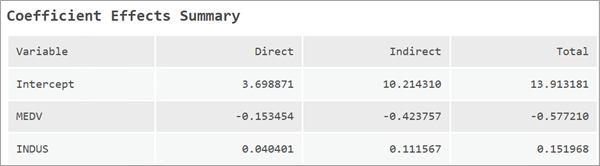
L’impact direct détermine dans quelle mesure un changement d’une unité dans une variable explicative affecte la valeur de la variable dépendante dans la localisation elle-même. Dans le cas d’impacts simples, cette valeur correspond au coefficient bêta.

L’impact indirect quant à lui détermine dans quelle mesure un changement d’une unité dans une variable affecte la variable dépendante dans ses localisations voisines. Notez cependant que la valeur des impacts est fortement influencée par la matrice de pondérations spatiales.

Erreurs standard

Par défaut, le modèle de décalage spatial renvoie les erreurs standard robustes. Toutefois, après l’ajustement d’un modèle de décalage spatial, il reste une forte auto-corrélation dans les valeurs résiduelles. Le test AK (Anselin-Kelejian) est un test de diagnostic permettant de déterminer s’il reste un montant significatif de dépendance spatiale dans les valeurs résiduelles du modèle.

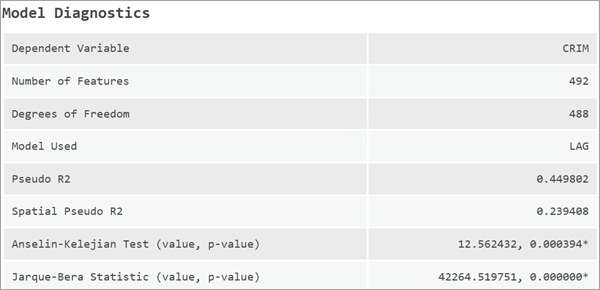
Si le test AK est significatif (valeur p inférieure à 0,05), une autre mesure d’erreur standard, appelée erreurs standard HAC (hétéroscédastiques et résistantes à l’auto-corrélation), est renvoyée. Les erreurs standard HAC représentent une variante non paramétrique des erreurs standard qui sont utiles en présence d’auto-corrélation spatiale.

Les erreurs standard HAC prennent en compte la distribution spatiale des données à l’aide d’une matrice de pondérations spatiales distincte. La matrice de pondérations spatiales est créée à l’aide des k voisins les plus proches pour identifier le voisinage de chaque entité avec l’entité focale incluse dans le voisinage. Les pondérations de chaque voisinage sont modélisées à l’aide d’un noyau triangulaire.

Pseudo R-carré et pseudo R-carré spatial

Le modèle de décalage spatial incluant le décalage spatial de la variable dépendante comme une variable explicative, les méthodes traditionnelles de prévision par régression linéaire ne peuvent pas être utilisées. Prédire la variable dépendante à l’aide de son décalage conduit à des estimations présomptueuses. Pour éviter cela, une autre mesure, appelée pseudo R-carré spatial, est calculée.

Le pseudo R-carré spatial est calculé sans le décalage spatial de la variable dépendante. Au lieu de cela, il utilise la matrice de pondérations spatiales et l’estimation de λ pour créer une valeur prédite de W_y-hat, utilisée à la place de W_y dans la prévision.

Les valeurs prévues sont alors utilisées pour calculer une valeur de pseudo R-carré traditionnelle. Il est recommandé d’indiquer la valeur de pseudo R-carré spatial plutôt que la valeur de pseudo R-carré.

Notez bien que le pseudo R-carré spatial est une mesure différente du R-carré ajusté renvoyé par les résultats du modèle OLS. Il n’est donc pas approprié de comparer ces deux mesures.

Interpréter les résultats du modèle d’erreur spatiale

Dans le modèle d’erreur spatiale, les coefficients de régression peuvent être interprétés de la même manière que ceux d’une régression linaire standard. Chaque coefficient représente le changement dans la variable dépendante par changement d’une unité dans la variable indépendante. Toutefois, le modèle SEM inclut également un composant supplémentaire, Lag Residual (lambda) (Résidu de décalage [lambda]), qui joue un rôle crucial pour comprendre la dépendance spatiale à l’intérieur du modèle. Le coefficient de Lag Residual (lambda) (Résidu de décalage [lambda]) est toujours compris entre -0,99 et 0,99.

Une valeur lambda positive suggère que les valeurs résiduelles présentent une agrégation spatiale, tandis qu’une valeur lambda négative indique que les valeurs résiduelles présentent une dispersion spatiale. Des valeurs absolues supérieures (positives ou négatives) de lambda suggèrent également que des processus spatiaux ne sont pas pris en compte par les variables explicatives. Inclure d’autres variables explicatives appropriées peut permettre de réduire le coefficient à des niveaux plus modérés.

Interpréter les résultats du modèle combiné d’auto-régression spatiale

Si le modèle SAC est sélectionné, toutes les sections applicables aux modèles SLM et SEM sont affichées dans les messages.

Bibliographie

Les ressources suivantes ont été utilisées pour implémenter l’outil :

• Anselin, L. et Sergio J. Rey. 2014. "Modern spatial econometrics in practice: A guide to GeoDa, GeoDaSpace and PySAL." ISBN 9780986342103.

• Bivand, Roger et Gianfranco Piras. 2015. "Comparing implementations of estimation methods for spatial econometrics." Journal of Statistical Software. 63: 1-36. https://doi.org/10.18637/jss.v063.i18.

• Kelejian, Harry H. et Ingmar R. Prucha. 2007. "HAC estimation in a spatial framework." Journal of Econometrics. 140, no. 1: 131-154. https://doi.org/10.1016/j.jeconom.2006.09.005.

• Smith, Tony E. 2009. "Estimation bias in spatial models with strongly connected weight matrices." Geographical Analysis. 41, no. 3: 307-332. https://doi.org/10.1111/j.1538-4632.2009.00758.x.