Fonctionnement de l’outil Estimer le temps avant l’événement

L’outil Estimer le temps avant l’événement prévoit le temps jusqu’à la survenue d’un événement pour un ensemble d’observations en fonction des temps précédents avant la survenue de l’événement ainsi que des attributs spécifiques des observations. L’entrée doit être un mélange d’enregistrements qui ont expérimenté l’événement et d’enregistrements qui ne l’ont pas expérimenté. L’outil incorpore des variables explicatives et estime si elles raccourcissent ou allongent le temps jusqu’à l’événement. L’outil prévoit également le temps supplémentaire jusqu’à la survenue de l’événement pour des observations qui n’ont pas encore expérimenté l’événement.

This video was created with ArcGIS Pro 3.5.

Chaque observation dans la table ou les entités en entrée doit comporter des champs contenant l’ancienneté de l’observation, un indicateur précisant si l’événement est déjà survenu et des variables explicatives. Ces champs sont fournis dans les paramètres Champ d’ancienneté, Champ d’indicateur d’événement et Variables explicatives, respectivement. Les variables explicatives peuvent être continues ou catégorielles et l’indicateur d’événement doit uniquement prendre les valeurs 0 (l’événement ne s’est pas produit) ou 1 (l’événement s’est produit). Pour le champ d’ancienneté, il s’agit souvent de l’âge réel du sujet, mais en général, cela correspond au délai entre la première date/heure possible où l’événement aurait pu survenir et la date/l’heure où il s’est réellement produit (ou la date/l’heure actuelle, si l’événement ne s’est pas produit). Par exemple, pour estimer la durée de vie des arbres, les valeurs du champ d’ancienneté doivent être l’âge actuel de l’arbre s’il est toujours vivant ou l’âge de l’arbre lors de sa mort. Toutefois, pour estimer le temps jusqu’à une nouvelle arrestation, les valeurs du champ doivent être le délai écoulé depuis que le sujet a été remis en liberté (première fois qu’une nouvelle arrestation peut avoir lieu) jusqu’à la date de sa nouvelle arrestation (ou la date actuelle si le sujet n’a pas fait l’objet d’une nouvelle arrestation). L’unité de l’ancienneté (heures, jours, années, etc.) n’a pas besoin d’être spécifiée, mais tous les résultats doivent être interprétés dans cette unité de temps.

L’outil produit différentes sorties, numériques et graphiques, pour comprendre comment les variables explicatives affectent le temps jusqu’à l’événement, pour prévoir à quel moment l’événement va se produire et pour évaluer l’exactitude et la fiabilité du modèle.

Applications possibles

Les modèles de temps de survie sont utiles dans différents domaines où l’objectif est d’estimer le délai nécessaire pour qu’un événement se produise et quels sont les facteurs qui influent sur ce délai. Voici certaines des applications possibles de l’outil :

• Maintenance d’infrastructure : estimez le délai avant qu’une fuite de canalisation ne survienne, qu’un pont ne nécessite une réparation importante ou qu’un transformateur ne tombe en panne. Les variables explicatives peuvent inclure le type de matériau (variable catégorielle), l’exposition à des conditions météorologiques extrêmes (variable catégorielle) et le volume de trafic (variable continue).
• Gestion forestière : modélisez le délai avant qu’un arbre n’atteigne un diamètre en particulier, n’ait besoin d’être prélevé ou ne succombe à une maladie. Les variables explicatives peuvent inclure le diamètre initial du tronc (variable continue), l’espèce (variable catégorielle), la qualité du sol (variable continue) et la concurrence avec les arbres voisins (variable catégorielle).
• Contrat d’échange sur risque de défaut de crédit : prévoyez le délai avant qu’un emprunteur ne puisse plus rembourser un prêt. Les variables explicatives peuvent inclure le montant du prêt (variable continue), la cote de solvabilité (variable continue), le type d’emploi (variable catégorielle) et l’historique des paiements passés (variable catégorielle).
• Rétention de la clientèle : estimez à quel moment un client va résilier un abonnement ou changer de fournisseur de service. Les variables explicatives peuvent inclure le montant mensuel facturé (variable continue), la durée du contrat (variable catégorielle), le nombre de plaintes adressées au service client (variable continue) et les remises promotionnelles reçues (variable catégorielle).
• Industrie : prévoyez à quel moment une machine devra faire l’objet d’une maintenance ou être remplacée. Les variables explicatives peuvent inclure les heures de fonctionnement (variable continue), le modèle de la machine (variable catégorielle) et la température de l’usine (variable continue).

Analyse du temps jusqu’à l’événement et analyse de survie

L’analyse du temps jusqu’à l’événement est une branche de statistiques qui estime, explique et prévoit quand un événement va se produire pour un ensemble d’observations, pour lesquelles on suppose que chaque observation expérimentera l’événement au bout d’un certain délai. L’analyse du temps jusqu’à l’événement est principalement utilisée dans la recherche médicale, où elle est couramment nommée analyse de survie car l’événement modélisé est le décès d’un sujet. C’est pour cette raison que la majeure partie de la terminologie et des concepts de l’analyse du temps jusqu’à l’événement est empruntée à l’analyse de survie. Par exemple, le délai écoulé jusqu’à ce que l’observation expérimente l’événement s’appelle sa durée de vie et la courbe qui estime le temps jusqu’à l’événement est appelée courbe de survie. Pour des applications qui prévoient la mort d’un arbre ou le moment où une infrastructure tombera en panne, la terminologie convient naturellement, mais cela est moins clair, par exemple, pour estimer le temps jusqu’à une nouvelle arrestation. Dans ce cas, le temps de survie d’un sujet correspondrait au délai écoulé avant que le sujet ne soit de nouveau arrêté. De même, on formulerait la probabilité qu’un sujet reste libre au moins cinq ans avant de se faire de nouveau arrêter comme la probabilité que le temps de survie dépasse cinq ans. Selon le contexte, cette rubrique abordera à la fois le temps avant des événements et les temps de survie, mais ces deux termes doivent être interprétés comme se rapportant au même concept.

Autre différence entre l’analyse du temps jusqu’à l’événement et l’analyse de survie : l’analyse de survie porte principalement sur l’estimation de l’effet d’un traitement (généralement un médicament dans le cadre d’essais cliniques) sur le temps de survie et porte moins sur la prévision des temps de survie de sujets individuels. Fondamentalement, la question est de savoir si le médicament augmente le temps de survie, et pas particulièrement combien de temps un sujet donné va vivre. L’analyse du temps jusqu’à l’événement porte cependant davantage sur la prévision du moment où l’événement va se produire pour des observations individuelles et moins sur l’estimation de l’influence des variables explicatives sur l’allongement ou la réduction du temps de survie. Bien que tous les modèles d’analyse de survie puissent être utilisés pour l’analyse du temps jusqu’à l’événement (et inversement), certains modèles conviennent mieux que d’autres. Spécifiquement, cet outil utilise un modèle paramétrique de temps de défaillance accéléré qui est plus adapté pour prévoir le temps jusqu’à l’événement, tandis que les essais cliniques utilisent généralement un modèle non paramétrique de Cox à risques proportionnels qui convient mieux pour estimer l’effet de traitements médicaux.

Courbes de survie

Lors de l’estimation du temps jusqu’à l’événement, une courbe de survie est créée pour chaque observation, selon leurs variables explicatives. La courbe de survie est une fonction qui représente la probabilité que le temps de survie dépasse un délai donné (en d’autres termes, la probabilité que le sujet reste en vie après un temps donné). La courbe de survie commence toujours à 1 et décroît au fil du temps jusqu’à 0. Par exemple, la courbe de survie suivante ressemble à celle des êtres humains :

Dans cette courbe, la grande majorité des sujets survivent après l’âge de 20 ans, puis la proportion commence à s’accélérer en décroissant. À l’âge de 60 ans, légèrement moins de 80 pour cent des sujets seront toujours en vie. Le temps de survie médian (0,5 sur l’axe y) est d’environ 80 ans. À 100 ans, il ne reste presque plus aucun sujet.

N’importe quel quantile du temps jusqu’à l’événement peut être calculé à partir de la courbe de survie. Par exemple, le 5^e centile du temps jusqu’à l’événement est la valeur de l’axe x lorsque la courbe équivaut à 0,95 (où la probabilité que l’événement n’ait pas encore eu lieu est de 95 pour cent) et le 75^e centile coïncide avec le moment où la courbe équivaut à 0,25. Ces quantiles peuvent servir à créer des intervalles de confiance. Par exemple, le temps entre le 5^e et le 95^e centiles est un intervalle de confiance de 90 pour cent pour le temps jusqu’à l’événement. Alors qu’il est possible de calculer n’importe quel quantile, les courbes de survie sont souvent synthétisées par le temps de survie médian (la valeur de l’axe x lorsque la courbe de survie est égale à 0,5).

Modèle de temps de défaillance accéléré

Le modèle statistique qui permet d’estimer les temps jusqu’à l’événement se nomme un modèle de temps de défaillance accéléré (AFT, Accelerated Failure Time). Les modèles AFT supposent que chaque observation prend de l’âge à une vitesse différente, selon ses variables explicatives individuelles Par exemple, on dit souvent (même si cela n’est pas vrai) que les chiens vieillissent sept fois plus vite que les êtres humains, qu’un chien de 3 ans est à un moment de sa vie qui équivaut à 21 ans chez les humains. Autre exemple : les rythmes de dégradation de deux ponts peuvent être considérés comme différents. Un pont peut avoir 30 ans et son niveau de dégradation peut être considéré comme équivalent à celui d’un autre pont de 10 ans seulement, selon les attributs des ponts (matériau de construction, volume du trafic et conditions environnementales).

Dans les modèles AFT, l’effet des variables explicatives consiste à accélérer ou à ralentir le temps jusqu’à l’événement, et cela s’exprime sous la forme d’un ratio de temps. Le ratio de temps entre deux observations A et B (chacune avec des variables explicatives différentes) est le ratio des durées de vie attendues de A et de B. Par exemple, un ratio de temps égal à 1,3 signifie que la durée de vie de l’observation A est supposée être 30 pour cent plus longue que celle de B. De même, un ratio de temps de 0,6 signifie qu’elle est censée être 40 pour cent plus courte. Un ratio de temps égal à 1 signifie que les deux observations sont censées avoir la même durée de vie. Notez que le ratio de temps implique une ligne de base ou référence de comparaison (dans ce cas, la durée de vie de l’observation B).

Le ratio de temps a pour effet d’étirer horizontalement la courbe de survie. Par exemple, l’image ci-dessous affiche quatre courbes de survie qui montrent l’effet des ratios de temps égaux à 1 (la courbe bleue qui sert de référence de comparaison), 2 (courbe orange), 3 (courbe verte) et 4 (courbe rouge), de gauche à droite. Il est difficile de voir que les courbes sont des versions étirées les unes des autres, une ligne horizontale en pontillés est donc tracée au niveau du temps de survie médian. Notez que le temps de survie médian pour le ratio de temps 2 est égal à deux fois le temps médian du ratio de temps 1. De même, les temps de survie médians pour les ratios de temps 3 et 4 sont égaux à trois et quatre fois le temps de survie médian du ratio de temps 1, respectivement. Même si la ligne en pointillés est placée au niveau médian, l’utilisation d’une autre valeur de l’axe y conserve également ces ratios.

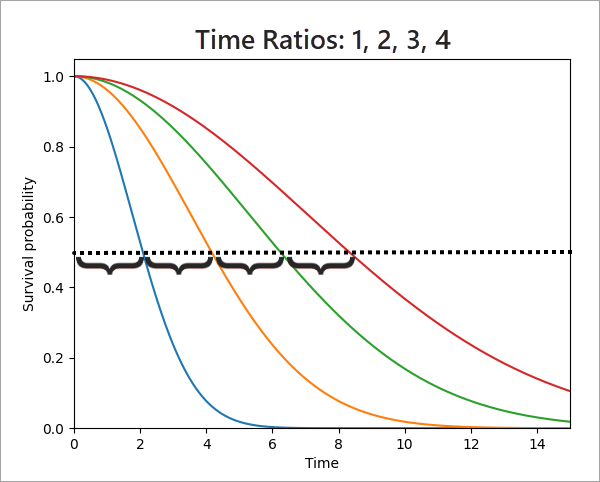
L’utilisation de la courbe bleue la plus à gauche comme référence est un choix arbitraire. Si la courbe rouge la plus à droite était définie à la place comme référence de comparaison, les ratios de temps seraient de 0,25, de 0,5, de 0,75 et de 1 (de gauche à droite). Ces ratios de temps inférieurs à 1 indiquent que la courbe de survie rouge bénéficie de la plus longue survie attendue des quatre courbes.

L’outil estime un ratio de temps pour chaque variable explicative, teste la signification statistique du ratio de temps et affiche le résultat dans les messages (consultez la section Messages de géotraitement ci-dessous pour en savoir plus). L’interprétation du ratio de temps varie selon que la variable explicative est catégorielle ou continue, car ces variables définissent leurs références de façon différente. Pour les variables catégorielles, l’une des catégories doit être désignée comme catégorie de référence. Des ratios de temps seront créés pour toutes les autres catégories par rapport à la catégorie de référence. Par exemple, si un champ de variable catégorielle a des valeurs uniques A, B et C et que la catégorie A est la catégorie de référence, les ratios de temps seront calculés uniquement pour les catégories B et C. Si le ratio de temps pour la catégorie B est de 2,2, cela signifie qu’une observation de la catégorie B est estimée vivre 2,2 fois plus longtemps qu’une observation dans la catégorie A, en supposant que tous les autres attributs sont égaux (ou que les courbes de survie pour la catégorie B ont un étirement 2,2 fois plus large que celui des courbes de survie de la catégorie A). L’outil utilise la première catégorie triée par ordre alphanumérique comme catégorie de référence, mais vous pouvez reclasser les valeurs de champ pour changer la catégorie utilisée comme catégorie de référence.

Pour les variables continues, le ratio de temps est le changement de durée de vie pour une augmentation d’une unité dans la variable explicative. Dans ce cas, la comparaison s’effectue entre deux observations dont la valeur de la variable explicative diffère de 1 exactement (toutes les autres variables explicatives étant égales). Dans le cas de l’estimation de la durée de vie d’un arbre, par exemple, si le diamètre du tronc en mètres est une variable explicative, le ratio de temps mesure l’allongement (ou la réduction) de la durée de vie en augmentant le diamètre de l’arbre de 1 mètre. Si les arbres dont le diamètre des troncs est plus important tendent à vivre plus longtemps, le ratio de temps sera supérieur à 1 et s’ils tendent à vivre moins longtemps, le ratio de temps sera inférieur à 1. Comme le ratio de temps est un multiplicateur, une augmentation de deux unités dans la variable explicative augmentera la durée de vie par le ratio de temps au carré. Une augmentation de trois unités de la variable explicative augmentera la durée de vie par le ratio de temps à la puissance trois et ainsi de suite. Cette nature complexe du ratio de temps pour les variables explicatives continue peut entraîner des difficultés de modélisation (consultez la section Pratiques conseillées, limitations et processus suggéré ci-dessous pour plus d’informations et obtenir des recommandations).

Estimation du modèle AFT

Le modèle AFT utilise une distribution de Weibull pour modéliser la courbe de survie :

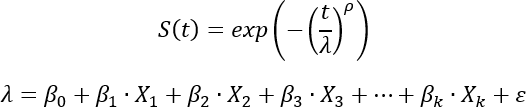
Le paramètre d’échelle (λ) est estimé comme un modèle linéaire des variables explicatives (X_i) et des coefficients estimés (β_i). C’est le paramètre d’échelle qui contrôle le degré d’étirement de la courbe de survie, comme décrit dans la section précédente. Intuitivement, les attributs particuliers d’une observation étirent (ou contractent) la courbe de survie de cette observation, selon que ses attributs sont associés de façon générale à des durées de vie plus longues ou plus courtes.

Le paramètre de forme (ρ) est partagé par toutes les observations et permet à la courbe de survie d’adopter différentes formes au cours de la même période. L’image suivante montre différentes formes pour des distributions de Weibull avec le même paramètre d’échelle :

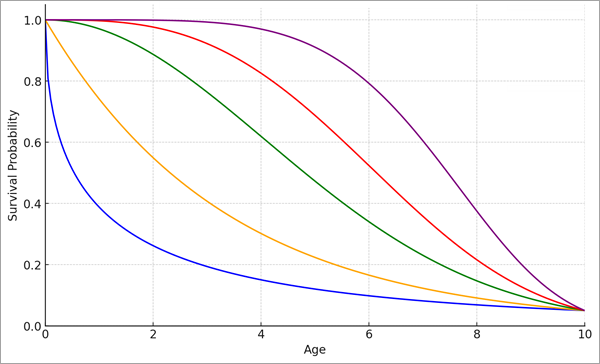
Le paramètre de forme est parfois nommé paramètre d’accélération car il est lié à l’accélération ou au ralentissement de la courbe de survie. L’accélération est mesurée par la fonction de risque, qui est définie comme la probabilité que l’événement se produise à un moment donné, en supposant que l’événement ne s’est pas produit avant cet instant. Par exemple, si les ponts plus anciens sont plus susceptibles de nécessiter des réparations dans un avenir proche que les ponts plus récents, la fonction de risque augmente avec le temps (en d’autres termes, les ponts plus anciens présentent des risques plus élevés que les ponts plus récents). La courbe de survie s’accélère donc au fil du temps. À l’inverse, si les ponts plus anciens sont moins susceptibles de nécessiter des réparations dans un avenir proche que les ponts plus récents, le taux de risque décroît et la courbe de survie ralentit. Des valeurs supérieures à 1 du paramètre de forme désignent une courbe de survie qui s’accélère et des valeurs inférieures à 1 indiquent une courbe de survie qui ralentit. Toutefois, le modèle ne peut pas estimer des taux de risque variables, où la courbe de survie s’accélère et ralentit à la fois à différents moments (par exemple, les durées de vie humaines présentent des risques plus élevés pour les nourrissons, puis des risques moindres pour les enfants et les jeunes adultes, puis à nouveau des risques plus élevés pour les adultes plus âgés).

Tous les coefficients et le paramètre de forme sont estimés sur la base de la probabilité maximale et sont affichés sous forme de messages par l’outil.

Observations censurées et prévision

Les sections précédentes ont expliqué comment les courbes de survie sont estimées pour chaque observation, que l’événement soit déjà survenu ou non pour l’observation. Par exemple, une courbe de survie peut être créée pour un pont qui est déjà endommagé. En substance, cette courbe de survie montre la durée de vie attendue du pont s’il avait été construit avec les mêmes attributs qu’aujourd’hui. Si ces informations sont utiles, il est beaucoup plus utile de créer des courbes de survie qui prévoient les durées de vie supplémentaires d’observations où l’événement ne s’est pas produit (par exemple, prévoir combien de temps encore un pont existant va durer avant de devoir être réparé).

Les observations dans lesquelles l’événement ne s’est pas encore produit sont appelées observations censorées et les observations dans lesquelles l’événement est survenu sont appelées observations non censorées Cette terminologie provient du fait que les informations des observations non censurées sont complètes (leur temps de survie est connu), mais que celles des observations censurées sont partielles : le temps de survie exact n’est pas connu, mais on sait qu’il est plus long qu’un certain délai (l’ancienneté actuelle de l’observation). L’idée, c’est qu’un document peut être non censuré ou censuré : toutes les informations contenues dans le document peuvent être disponibles (document non censuré) ou certaines parties de ces informations peuvent être occultées par un censeur (document censuré).

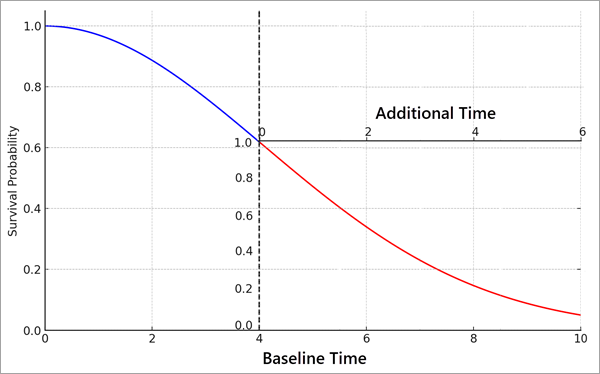
Pour les observations censurées, l’objectif est de créer une courbe de survie qui estime le temps supplémentaire jusqu’à l’événement, étant donné son ancienneté actuelle. Cette courbe de survie supplémentaire peut être construite en s’appuyant sur le délai de survie déjà écoulé pour le sujet. La formule mathématique pour le calcul de la courbe du temps de survie supplémentaire, S_Add(T), est S_Add(T) = S(C+T)/S(C), pour les unités temporelles supplémentaires T après le moment de la censure C.

La courbe du temps de survie supplémentaire peut être représentée comme une remise à l’échelle de la courbe de survie de l’observation après le moment de la censure. L’image ci-dessous montre par exemple une courbe de survie d’une observation qui a été censurée au temps 4. Selon les variables explicatives, la probabilité était d’environ 60 pour cent pour que le sujet vive au moins quatre unités de temps (la valeur sur l’axe au moment de la censure). Cependant, comme on sait que le sujet a survécu au moins quatre unités de temps (moment de la censure), les valeurs de l’axe y sont remises à l’échelle pour redémarrer à 1 (en d’autres termes, la probabilité est de 100 pour cent pour que le sujet a survécu au moins quatre unités de temps). De même, l’axe x commence à 0 pour mesurer le futur à partir du moment de la censure. Dans cet exemple, le temps de survie médian d’un sujet avec ces variables explicatives est d’environ cinq unités de temps (où la courbe croise 0,5 sur l’axe y d’origine), mais si l’on sait que le sujet a déjà survécu quatre unités de temps, le temps de survie supplémentaire médian est d’environ deux unités de temps (où la courbe croise 0,5 sur l’axe y remis à l’échelle de taille inférieure) pour une durée de vie totale de six unités de temps. En d’autres termes, le fait de savoir que le sujet a déjà survécu pendant quatre unités de temps augmente la durée de vie médiane totale d’environ cinq unités de temps à environ six unités de temps. Plus l’observation survit longtemps avant d’être censurée et plus elle est censée survivre longtemps par rapport à sa courbe de survie de référence.

Pour les observations censurées, les courbes de survie qui présentent les temps supplémentaires jusqu’à l’événement après la censure s’affichent dans des diagrammes contextuels de la table ou des entités en sortie. Pour les entités censurées et non censurées, les courbes de survie individuelles s’affichent également dans des diagrammes contextuels.

L’ancienneté de l’observation au moment de la censure est généralement l’ancienneté actuelle de l’observation, mais il peut également s’agir de l’ancienneté du sujet lors de sa dernière observation, par exemple la date la plus récente de l’inspection d’un pont. Dans ce cas, le temps de survie supplémentaire démarre à l’ancienneté de l’observation lorsqu’elle a été observée pour la dernière fois.

Courbe de Kaplan-Meier

Comme chaque combinaison de variables explicatives génère une courbe de survie différente, il peut être difficile de savoir si une observation en particulier est censée avoir une durée de vie plus longue ou plus courte qu’une observation type. Certaines des variables explicatives de l’observation augmentent la durée de vie et d’autres la raccourcissent, mais on ne sait pas exactement si, au total, elles allongent ou raccourcissent la durée de vie de l’observation. Pour fournir une courbe qui peut servir de base de comparaison par rapport à chaque courbe de survie, l’outil calcule une courbe de Kaplan-Meier pour les données.

La courbe de Kaplan-Meier est une estimation non paramétrique de la fonction de survie qui ignore les variables explicatives et évalue la proportion d’observations qui n’ont pas expérimenté l’événement au fil du temps. Pour ce faire, elle s’adapte séquentiellement à l’événement et aux moments de censure à l’aide de l’équation suivante :

Dans l’équation, E_i est le nombre d’événements qui se sont produits à l’instant t_i et N_i est le nombre d’observations qui n’ont pas expérimenté l’événement ou qui ont été censurées avant l’instant t_i.

La courbe est représentée sous forme de fonction en escalier qui décroît chaque fois que l’événement a lieu. La courbe ne peut pas s’étendre au-delà du moment où la valeur de champ d’ancienneté est la plus élevée et la probabilité de survie ne descendra jamais sous le pourcentage de sujets qui ont été censurés. Par exemple, dans la courbe de Kaplan-Meier ci-dessous, la valeur la plus élevée du champ d’ancienneté était d’environ 3 500 (la valeur maximale de l’axe x), et un peu plus de 40 pour cent des observations ont été censurées (la valeur la plus petite de la courbe est légèrement supérieure à 0,4).

La courbe de Kaplan-Meier pour les données s’affiche dans une section réductible des messages de géotraitement. Elle apparaît également dans les diagrammes contextuels de la table ou des entités en sortie pour pouvoir être directement comparée aux courbes de survie de chaque observation (reportez-vous à la section suivante pour plus d’informations).

Sorties de l’outil

L’outil renvoie différentes sorties qui permettent d’examiner les résultats. Les sorties sont notamment une table ou une classe d’entités en sortie, des messages de géotraitement, des diagrammes contextuels et un histogramme.

Entités ou table en sortie

Pour l’entité en entrée, la couche d’entités en sortie s’affiche en fonction du temps supplémentaire médian jusqu’à l’événement. Les entités censurées sont représentées en nuances de rouge et de rose avec des tons plus profonds qui indiquent que, selon les prévisions, l’événement doit se produire plus tôt. Les données non censurées sont représentées en gris clair et sont configurées de façon à apparaître sous les données censurées si leurs symboles se superposent.

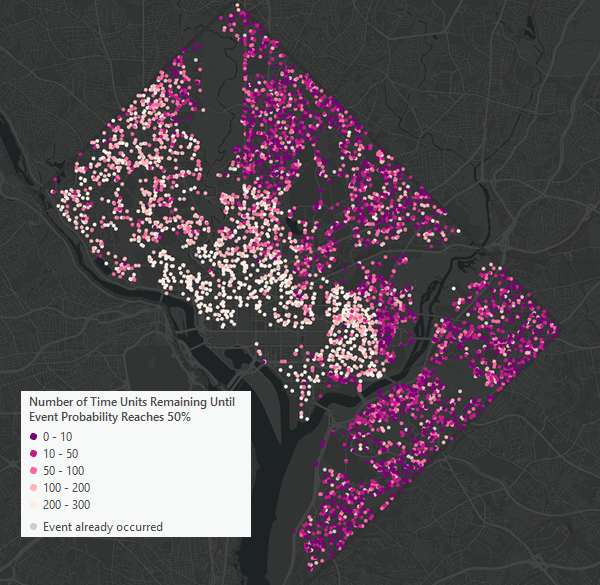
Pour la table et les entités en entrée, la sortie contiendra des copies de tous les champs en entrée, ainsi que différents quantiles du temps supplémentaire jusqu’à l’événement. Les champs comporteront le 5^e centile, le 10^e centile, le 25^e centile, la médiane (50^e), le 75^e centile, le 90^e centile et le 95^e centile du temps supplémentaire jusqu’à l’événement. Vous pouvez utiliser ces valeurs pour créer des plages correspondant à la survenue probable de l’événement. Utilisez par exemple le 5^e et le 95^e centiles pour construire un intervalle de confiance de 90. Pour les entités non censurées, toutes les valeurs du champ de quantile seront nulles car il n’est pas nécessaire de prévoir le moment de survenue de l’événement si celui-ci s’est déjà produit.

Diagrammes contextuels

Si le paramètre Activer les fenêtres contextuelles de la courbe de survie est activé, la table ou les entités en sortie contiendront également un champ de diagrammes contextuels pour chaque observation. Pour les entités, vous pouvez accéder aux diagrammes contextuels en cliquant sur l’entité dans la carte à l’aide de l’outil Explorer. Pour les tables, les diagrammes contextuels sont accessibles en cliquant avec le bouton droit sur la ligne de l’enregistrement dans la table attributaire.

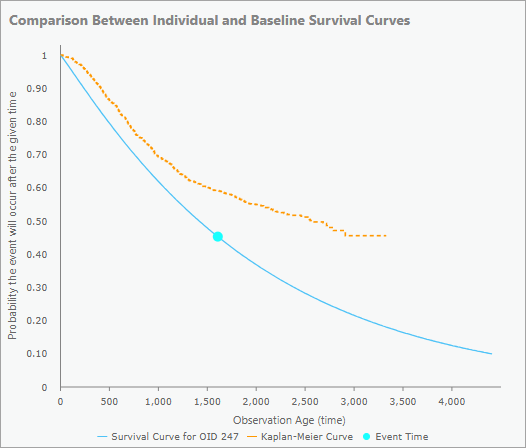
Pour les observations non censurées, le diagramme contextuel présente la courbe de survie de l’entité (courbe bleue) et un point bleu indiquant le moment de l’événement. Cela vous permet de voir si l’observation a expérimenté l’événement tôt ou tard dans sa durée de vie prévue. Les observations pour lesquelles les événements se sont produits beaucoup plus tôt ou plus tard que ce que le modèle avait prévu peuvent justifier un examen plus poussé. La courbe de Kaplan-Meier (courbe orange) est également incluse dans le diagramme contextuel comme base de comparaison. Cela vous permet de voir si l’observation était censée survivre plus ou moins longtemps qu’une observation type. Dans l’image ci-dessous par exemple, la courbe de survie est positionnée plus bas et à gauche de la courbe de Kaplan-Meier, ce qui signifie que l’événement était censé se produire plus tôt que pour la plupart des autres observations. Le point bleu se trouve également au milieu de la courbe de survie, ce qui signifie que l’événement a eu lieu à peu près quand le modèle l’avait prévu, sur la base de ses variables explicatives.

Remarque :

L’axe x des diagrammes contextuels s’étendra jusqu’à ce que la courbe de survie atteigne 0,1 (une valeur limite est nécessaire car les courbes de survie n’atteignent jamais zéro). Cependant, comme la courbe de Kaplan-Meier ne peut pas dépasser la valeur la plus élevée du champ d’ancienneté, il se terminera souvent avant que la courbe de survie n’atteigne 0,1. Pour que la courbe de Kaplan-Meier soit visible, l’axe x ne s’étendra jamais au-delà de deux fois la longueur de la courbe de Kaplan-Meier, même si la courbe de survie n’atteint toujours pas 0,1.

Pour les entités censurées, les diagrammes contextuels comporteront également la courbe de survie et la courbe de Kaplan-Meier pour l’observation, mais le moment de censure sera indiqué par un cercle bleu au lieu d’un point.

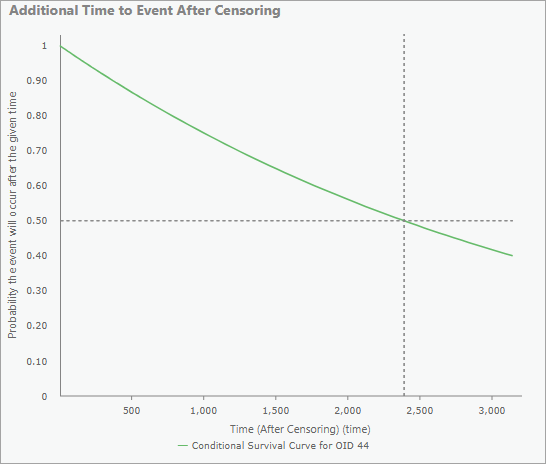
Pour les entités censurées uniquement, seuls les diagrammes contextuels comporteront également un diagramme du temps supplémentaire jusqu’à l’événement après la censure. Le temps supplémentaire médian est représenté sous forme de lignes horizontales et verticales en pointillés pour identifier le moment où le modèle prévoit avec une probabilité de 50 pour cent que l’événement se sera produit. L’axe x s’étendra jusqu’à ce que la courbe atteigne 0,4 pour que la médiane soit toujours visible.

Vous pouvez survoler les diagrammes contextuels pour voir certaines valeurs des courbes.

Messages de géotraitement

Les messages de géotraitement contiennent différentes sections qui récapitulent les effets des variables explicatives et des diagnostics sur le niveau d’adéquation du modèle aux données.

Variables explicatives continues

La première section des messages comporte une table qui récapitule les effets des variables explicatives continues. Pour chaque variable, la table affiche le ratio de temps, le coefficient et son erreur standard (à partir du paramètre d’échelle de la distribution de Weibull), le score z et la valeur p qui testent la signification statistique du coefficient, ainsi que les limites inférieure et supérieure d’un intervalle de confiance de 95 pour cent du ratio de temps.

Une ligne pour l’ordonnée à l’origine est incluse à la fin, mais les valeurs brutes n’ont généralement pas d’interprétation significative. À la place, l’objectif de l’ordonnée à l’origine est de mettre à l’échelle les courbes de survie sur l’unité temporelle du champ d’ancienneté. Par exemple, si vous avez converti les valeurs du champ d’ancienneté des heures en jours, tous les ratios de temps resteront identiques, mais le ratio de temps de l’ordonnée à l’origine sera divisé par 24 (la conversion des heures en jours). C’est pourquoi l’unité du champ d’ancienneté n’a pas besoin d’être spécifiée dans l’outil et les résultats obtenus seront équivalents quelle que soit l’unité.

Remarque :

Pour chaque variable, le coefficient et son erreur standard sont estimés directement par le modèle AFT. Leur signification statistique est testée à l’aide d’un test z. Le ratio de temps est ensuite calculé à partir du coefficient en prenant son exposant : exp(coefficent). Les ratios de temps sont généralement préférés aux coefficients car ils sont interprétés par rapport au temps de survie brut, tandis que les coefficients sont interprétés par rapport au logarithme du temps de survie. Les limites de confiance supérieure et inférieure sont calculées en créant un intervalle de confiance pour le coefficient et en calculant l’exposant des extrémités.

Variables explicatives catégorielles

La deuxième section des messages comporte des tables qui récapitulent les effets des variables explicatives catégorielles. Pour chaque variable catégorielle, une table présente l’effet de chacune de ses catégories. La catégorie de référence apparaît au-dessus de la table et tous les ratios de temps doivent être interprétés par rapport à cette catégorie. Dans l’image ci-dessous par exemple, la variable catégorielle est le numéro de salle et la salle 1 est la catégorie de référence. Les observations de la salle 2 subsistent 5,345 plus longtemps que les observations de la salle 1 (ratio de temps égal à 5,345), mais les observations de la salle 8 subsistent 23,6 pour cent moins longtemps que les observations de la salle 1 (ratio de temps égal à 0,764). Les valeurs p indiquent également que les salles 4, 5 et 7 ne sont pas sensiblement différentes de celles de la salle 1.

Remarque :

Chaque variable catégorielle est convertie en une série de variables binaires (0 et 1) et ces variables binaires sont utilisées comme variables explicatives continues dans le modèle AFT. Pour K catégories, des variables binaires (K-1) sont créées, et chaque catégorie reçoit une variable binaire sauf la catégorie de référence (ce processus se nomme l’encodage d’indicateur). Une catégorie doit être exclue et utilisée comme référence parce qu’inclure des variables binaires pour toutes les catégories entraîne une colinéarité parfaite, ce qui empêche le modèle d’estimer les coefficients et les ratios de temps.

Paramètre de forme de Weibull

Après les tables de coefficients des variables explicatives, les messages affichent une table qui récapitule le paramètre de forme de la distribution de Weibull. La table contient également le score z et la valeur p qui testent si le paramètre de forme est statistiquement différent de 1. Les limites inférieure et supérieure pour un intervalle de confiance de 95 pour cent sont également fournies.

Le paramètre de forme indique si la courbe de survie accélère ou ralentit. Les valeurs sensiblement supérieures à 1 indiquent une accélération, ce qui signifie que plus l’observation est ancienne et plus elle a de chances d’expérimenter l’événement dans un futur proche. Les valeurs sensiblement inférieures à 1 indiquent une décélération, ce qui signifie que les observations plus récentes ont plus de chances d’expérimenter l’événement dans un futur proche. Les valeurs qui ne sont pas sensiblement différentes de 1 indiquent que les observations récentes et anciennes ont autant de chances d’expérimenter l’événement dans un futur proche. Le modèle suppose que la courbe de survie accélère ou ralentit de façon constante, mais qu’elle ne peut pas passer de l’un à l’autre de ces états.

Statistiques du résumé du modèle

La section finale des messages est la section Résumé du modèle, qui contient des statistiques liées à l’exactitude globale des prévisions et de l’adéquation du modèle. La section affiche les statistiques suivantes :

• Indice de concordance : valeur comprise entre 0 et 1 qui indique la probabilité que le modèle puisse correctement prévoir si un sujet aura une durée de vie plus longue qu’un autre sujet. Les valeurs proches de 1 indiquent que le modèle peut presque toujours prévoir quel sujet expérimentera l’événement en premier et les valeurs proches de 0,5 indiquent que le modèle n’arrive pas mieux à prévoir l’ordre des événements que le pur hasard. Les valeurs inférieures à 0,5 sont rarement observées, mais signifient que les prévisions du modèle sont moins exactes que le pur hasard. Les valeurs sont calculées comme la proportion de paires de sujets où le modèle a prévu correctement lequel des deux sujets a expérimenté l’événement en premier. Les entités censurées ne sont pas utilisées dans le calcul car leur temps de survie n’est pas connu. En pratique, la valeur est généralement comprise entre 0,6 et 0,8.
• AIC : critère d'information d'Akaike pour l’adéquation du modèle AFT. Cette valeur est donnée principalement à titre d’information, mais elle peut être utilisée dans des processus avancés, par exemple pour construire des tests de rapport de vraisemblance imbriqués entre différentes combinaisons de variables explicatives.
• Valeur p : valeur p d’un test de signification globale des variables explicatives. La valeur indique si les variables explicatives ensemble permettent d’améliorer de manière significative les prévisions du modèle. Si cette valeur n’est pas statistiquement significative (généralement une valeur supérieure à 0,05), le modèle ne fait pas beaucoup mieux que si aucune variable explicative n’était fournie. La valeur est déterminée à l’aide d’un test de rapport des vraisemblances.

Histogramme des résidus de déviance

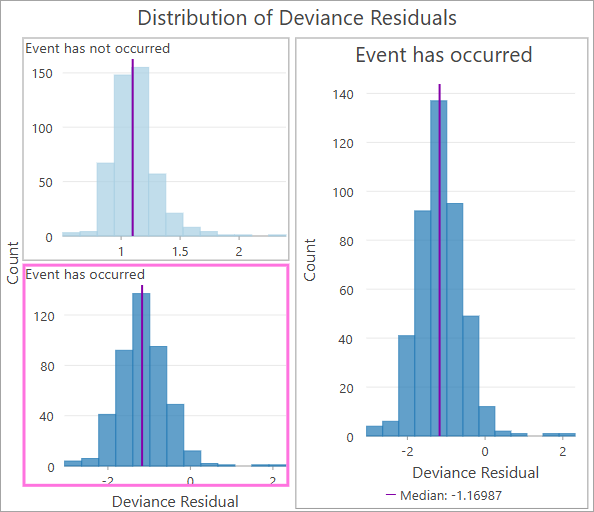
La couche d’entités en sortie inclut également un histogramme des résidus de déviance des observations. Les résidus de déviance sont conceptuellement similaires aux résidus dans d’autres modèles de régression en ce sens qu’ils indiquent si la durée de vie d’une observation a été plus longue ou plus courte que ce que le modèle avait prévu. Les résidus de déviance positifs signifient que le sujet a eu une durée de vie plus longue que prévu et les résidus de déviance négatifs signifient que le sujet a eu une durée de vie plus courte (notez que certaines sources définissent les signes, positifs ou négatifs, dans l’autre sens). En cas d’adéquation satisfaisante du modèle, la moyenne des résidus de déviance doit être proche de zéro.

Pour les observations non censurées, certaines auront des durées de vie plus longues ou plus courtes que les prévisions du modèle, de sorte que leurs résidus de déviance peuvent être à la fois positifs et négatifs. Toutefois, les résidus de déviance des observations censurées seront toujours positifs. C’est pour cette raison que l’histogramme est fractionné par le champ d’indicateur d’événement, affichant des histogrammes distincts pour les observations censurées et non censurées.

Les résidus de déviance sont les plus utiles pour étudier les points aberrants dans les résultats. Les valeurs extrêmes dans les deux histogrammes indiquent différentes choses. Pour les observations non censurées, des valeurs négatives extrêmes indiquent que l’observation a expérimenté l’événement beaucoup plus tôt que ce qui était prévu par le modèle et des valeurs positives extrêmes indiquent qu’elle a expérimenté l’événement beaucoup plus tard. Les valeurs supérieures à trois dans l’un ou l’autre sens indiquent probablement des points aberrants ou des observations anormales qui peuvent mériter un examen plus poussé ou leur retrait du jeu de données. Pour les observations censurées, les valeurs sont moins significatives, mais elles mesurent généralement le chemin parcouru par l’observation le long de sa durée de vie avant d’être censurées. Les valeurs situées à l’extrême gauche (celles proches de zéro) indiquent que l’observation a été censurée tôt au cours de sa durée de vie et les valeurs situées à l’extrême droite indiquent qu’elle a été censurée tard au cours de sa durée de vie (elle a probablement déjà vécu plus longtemps que ce que le modèle avait prévu, même avant d’être censurée).

Les résidus de déviance sont calculés à l’aide de l’équation suivante :

Dans l’équation, S-hat_i(t_i) est la probabilité de survie estimée de l’observation au moment de l’événement (ou au moment de sa censure) et δ_i est l’indicateur d’événement.

Remarque :

Les résidus de déviance pour les observations censurées sont toujours positifs car si un sujet a déjà survécu pendant un laps de temps donné, on prévoit qu’il a une durée de vie totale plus longue que ce que prévoit sa courbe de survie de référence (voir l’image de la section Observations censurées et prévision ci-dessus pour comprendre pourquoi). Ce traitement garantit que la moyenne globale des résidus de déviance (observations censurées et non censurées) est égale à zéro pour les modèles spécifiés correctement.

Pratiques conseillées, limitations et processus suggéré

L’outil s’accompagne d’un certain nombre de limitations et de défis que vous pouvez rencontrer. Voici les recommandations générales et les pratiques conseillées pour utiliser l’outil :

• Prévoir quand un événement va se produire étant une tâche naturellement difficile, nous vous engageons à nourrir des attentes réalistes. L’outil peut uniquement extraire des informations des variables explicatives que vous fournissez, mais des phénomènes complexes tels qu’une panne d’infrastructure impliquent de nombreux facteurs qui sont généralement très locaux et propres à chaque sujet. En pratique, vous devez considérer les temps prévus jusqu’à l’événement comme des indications générales du moment où l’événement risque de se produire, et non comme des prévisions très spécifiques de dates données. Vous devez également être particulièrement prudent et faire preuve de scepticisme lorsque vous extrapolez des temps avant l’événement supérieurs au temps avant l’événement le plus long dans les données en entrée. Même s’ils sont souvent imprécis, les résultats d’une analyse du temps jusqu’à l’événement peuvent toujours être très utiles pour fournir des estimations générales des coûts futurs ou pour prioriser et allouer des ressources aux observations les plus susceptibles d’être les prochaines à expérimenter l’événement.

• Les modèles de temps de survie ne sont pas intrinsèquement spatiaux, mais l’incorporation d’informations spatiales peut les améliorer par la prise en compte de modèles géographiques. Envisagez d’ajouter des variables explicatives spatiales, telles que des régions géographiques comme variables explicatives catégorielles ou des distances par rapport à des entités clés comme variables explicatives continues. Pour modéliser la mortalité des arbres en milieu urbain, par exemple, la distance par rapport au bâtiment le plus proche peut être importante car l’ombre d’un bâtiment peut réduire la lumière du soleil.

• Le modèle suppose que l’événement se produira pour chaque observation après un certain délai, mais il arrive parfois que cela ne soit pas vrai. Par exemple lorsque vous prévoyez le temps jusqu’à une nouvelle arrestation, certains sujets ne feront jamais l’objet d’une nouvelle arrestation, mais le modèle va quand même prévoir une courbe de survie à leur intention. En pratique, si le temps supplémentaire prévu pour la survie d’une observation est très long, cela peut signifier que l’événement a des chances de ne jamais avoir lieu.
• Pour les variables explicatives continues, les ratios de temps sont le changement multiplicatif dans la courbe de survie pour une augmentation d’une unité dans la variable explicative. Pour certaines variables toutefois, un changement d’une unité est minuscule et les résultats dans les ratios de temps très proches de 1 même pour les variables explicatives très significatives et importantes. Par exemple lorsque vous prévoyez le moment où des toits devront être réparés, vous pouvez utiliser la taille du bâtiment en mètres carrés comme variable explicative. Toutefois, même si la taille du bâtiment est très importante, une augmentation d’un seul mètre carré n’aura qu’un effet restreint sur la courbe de survie. Si l’une de vos variables explicatives est très significative (score z élevé et valeur p faible), mais que son ratio de temps imprimé est égal à 1,000 ou approchant, vous pouvez diviser les valeurs du champ par une valeur élevée constante. Par exemple, si vous divisez la variable en mètres carrés par 100, vous générez des courbes de survie identiques et des résultats significatifs, mais le ratio de temps sera maintenant interprété comme le changement de taille du bâtiment pour une augmentation de 100 mètres carrés, ce qui peut produire un ratio de temps plus lisible. Comme la multiplication ou la division des variables explicatives (ou du champ d’ancienneté) par une valeur constante produit des courbes de survie équivalentes, nous vous encourageons à remettre à l’échelle les valeurs si cela permet de mieux interpréter les résultats.
• Comme le ratio de temps est multiplicatif, les valeurs élevées (par rapport aux valeurs du reste des données) de n’importe quelle variable explicative peuvent entraîner de l’instabilité et des courbes de survie déraisonnablement longues ou courtes. Le ratio de temps représente le changement pour une augmentation d’une unité dans la variable explicative, et cela évolue de manière exponentielle. Par exemple, une augmentation de cinq unités dans la variable explicative étire la courbe de survie par le ratio de temps à la puissance cinq. Pour les valeurs élevées de la variable explicative, ces exposants peuvent devenir très importants et produire des courbes de survie instables. Les points aberrants seront particulièrement problématiques, mais même les valeurs élevées qui ne sont pas des points aberrants peuvent générer des courbes de survie instables. Dans ce cas, il est possible d’appliquer une transformation logarithmique à la variable explicative. Cela rendra le ratio de temps de la variable explicative plus difficile à interpréter (c’est maintenant l’étirement de la courbe de survie pour une augmentation d’une unité dans le logarithme de la variable explicative), mais la conversion de la variable explicative en échelle logarithmique contrebalance généralement l’effet complexe du ratio de temps et produit des courbes de survie plus raisonnables.

• Bien que l’estimation des paramètres du modèle utilise à la fois des observations censurées et non censurées, les observations censurées fournissent le plus d’informations car leur temps de survie exact est connu. En règle générale, il est recommandé de disposer d’au moins 10 observations non censurées par variable explicative. Cependant, les variables catégorielles doivent compter comme plusieurs variables. Une variable catégorielle avec deux catégories compte comme une variable ; trois catégories compte comme deux variables ; quatre catégories comptent comme trois variables et ainsi de suite. En outre, chaque catégorie doit comporter plusieurs observations non censurées afin de mieux estimer l’effet de toutes les catégories de la variable catégorielle.

• Dans certains cas, il peut être difficile de définir le point de départ de la durée de vie d’une observation. Par exemple, des ponts doivent régulièrement faire l’objet de travaux de réparation et de maintenance. Lorsque vous prévoyez le temps qu’il reste avant de nouvelles réparations, la date de départ peut être la date de construction d’origine du pont ou la date à laquelle le pont a dû être réparé pour la dernière fois. Dans ce cas, vous devez décider si un pont réparé est considéré comme équivalent à un pont neuf. Si vous décidez que des ponts réparés et des ponts neufs sont équivalents, un seul pont peut être inclus dans les données plusieurs fois afin de construire le modèle (une fois pour chaque réparation qui a été nécessaire). Si vous décidez toutefois qu’un pont réparé et un pont neuf ne sont pas équivalents, vous pouvez essayer d’utiliser le nombre de fois précédentes que le pont a dû être réparé comme variable explicative.

Même s’il n’existe pas de processus idéal pour une analyse du temps jusqu’à l’événement, voici un modèle général pour créer et évaluer un modèle :

1. Examinez les données en entrée et choisissez les variables explicatives à utiliser. Sélectionnez des variables explicatives que vous pensez ou savez être liées au temps de survie et examinez-les au moyen de diagrammes. Des nuages de points de variables explicatives et du temps de survie seront particulièrement utiles pour déterminer quelles variables sont liées au temps de survie (malheureusement, seules les observations non censurées peuvent être utilisées dans ce cas). Soyez particulièrement attentifs aux points aberrants dans les variables explicatives continues. Vous pouvez les supprimer ou appliquer une transformation logarithmique. Pour les variables catégorielles, vérifiez qu’il existe plusieurs observations non censurées pour chaque catégorie et éventuellement fusionnez ou supprimez les catégories qui comportent peu d’observations non censurées.
2. Selon la façon dont les données sont représentées, une certaine ingénierie des données peut être requise pour créer les champs d’ancienneté et d’indicateur d’événement. Vous pouvez par exemple être amené à convertir les champs de dates de début et de fin en valeurs d’ancienneté (l’expression DateDiff Arcade dans l’outil Calculer un champ sera utile pour ce faire) ou à reclasser un champ de texte en champ d’indicateur d’événement binaire.
3. Après avoir exécuté l’outil et examiné les avertissements ou erreurs, vous devez vérifier l’exactitude globale du modèle et rechercher les signes d’adéquation insuffisante ou de spécification erronée du modèle. Examinez l’histogramme des résidus de déviance et faites particulièrement attention aux valeurs résiduelles extrêmes (positives ou négatives) qui se trouvent dans les observations non censurées. Évaluez la valeur p et l’indice de concordance dans la section Résumé du modèle des messages, et si la valeur p n’est pas significative (ce qui sera rarement le cas), essayez de trouver des variables explicatives qui estiment mieux les temps de survie. Vous devez également voir si la taille de l’indice de concordance est suffisamment élevée, afin que les attentes restent réalistes.
4. Si le modèle global est suffisamment exact, vous devez ensuite examiner les tables de coefficients dans les messages pour savoir quelles variables explicatives ont impacté les temps de survie et connaître le degré de leur impact. Vous pouvez supprimer les variables explicatives qui ne sont pas statistiquement significatives.
5. Pour les entités, explorez ensuite la couche d’entités en sortie dans une carte et recherchez des modèles spatiaux. Est-ce que certaines zones présentent des temps de survie plus longs que d’autres ?
6. Enfin, explorez les diagrammes contextuels et la table attributaire de chaque observation d’intérêt pour voir leurs courbes de survie estimées.

Bibliographie

Les ressources suivantes ont été utilisées pour implémenter l’outil :

• Collett, David. 2023. "Modelling survival data in medical research." Chapman and Hall/CRC. https://doi.org/10.1201/9781003282525.
• Davidson-Pilon, Cameron. 2019. "lifelines: survival analysis in Python." Journal of Open Source Software. 4(40), 1317, https://doi.org/10.21105/joss.01317.
• Klein, John P. et Melvin L. Moeschberger. 2003. "Survival Analysis: Techniques for Censored and Truncated Data." Springer Science & Business Media. ISBN 0-387-95399-X.