Fonctionnement de l’analyse d’inférence causale

L’outil Analyse d’inférence causale estime l’effet causal entre une variable d’exposition continue et une variable de résultat continue en équilibrant les variables de confusion. L’outil utilise l’appariement du score de propension ou la pondération par l’inverse du score de propension pour attribuer des pondérations à chaque observation de sorte que les variables de confusion ne soient plus corrélées avec la variable d’exposition, isolant l’effet causal existant entre l’exposition et le résultat. Le résultat est une fonction exposition-réponse (ERF) qui estime dans quelle mesure la variable de résultat réagit aux modifications de la variable d’exposition. Vous pouvez, par exemple, estimer l’augmentation moyenne du rendement du maïs (résultat) pour différentes doses d’engrais (exposition) et factorisez les variables de confusion telles que le type de sol, les techniques de production agricole et les variables environnementales qui influent sur la production du maïs. L’ERF apparaît sous forme d’une couche de graphiques et dans les messages de géotraitement. Par ailleurs, vous pouvez estimer l’effet causal d’observations individuelles et créer des objectifs axés sur les buts. Par exemple, vous pouvez estimer la quantité d’engrais dont chaque exploitation agricole a besoin pour produire un volume de maïs précis chaque année.

Contexte général de l’analyse d’inférence causale

L’analyse d’inférence causale est un champ des statistiques qui modélise les relations de cause à effet entre deux variables d’intérêt. Une variable (appelée variable d’exposition ou de traitement) modifie ou affecte directement une autre variable (connue sous le nom de variable de résultat). Les corrélations sont souvent utilisées pour mesurer la façon dont les modifications d’une variable sont associées aux modifications de l’autre variable. Toutefois, la corrélation ne signifie pas nécessairement qu’une variable est la cause de l’autre variable. Elles peuvent subir toutes les deux l’influence d’autres facteurs. Ainsi, la relation entre la vente de glaces et la vente d’écrans solaires peut être une relation positive forte. Cependant, vous ne pouvez pas en conclure qu’une hausse des ventes de glaces entraîne une hausse des ventes d’écrans solaires. D’autres facteurs, tels que la température, l’index UV ou le mois de l’année, doivent être pris en compte avant de tirer des conclusions de causalité. Les facteurs ayant une incidence à la fois sur la variable d’exposition et la variable de résultat sont appelées variables de confusion. Il est essentiel de les inclure et de les prendre en compte pour saisir précisément la relation de cause à effet existant entre les variables d’exposition et de résultat.

Une analyse causale commence par une hypothèse fondée sur la recherche ou les connaissances générales. Considérons, par exemple, l’effet de l’exercice physique sur la santé. Il est prouvé et communément admis que l’exercice physique régulier contribue à améliorer la santé, mais les variables dépendent également de nombreuses autres variables de confusion, telles que les habitudes alimentaires, le mode de vie et l’accès à des espaces sécurisés de pratique sportive. En pareille situation, l’analyse d’inférence causale permet d’isoler l’effet de la variable d’exposition (un exercice quotidien, par exemple) de la variable de résultat (un résultat en termes de santé, par exemple) après avoir pris en compte diverses variables de confusion importantes.

Au cours des procédures expérimentales, les variables de confusion sont contrôlées à l’aide d’essais contrôlés randomisés (ECR). Les ECR sont largement utilisés par la recherche clinique. Ils impliquent que les participants soient répartis dans des groupes ayant des variables de confusion similaires. Chaque groupe est ensuite soumis à différents niveaux d’exposition et leurs résultats sont comparés. Par exemple, un groupe fait de l’exercice à raison de 10 minutes par jour, un autre pendant une heure et un autre encore ne pratique aucune activité. Étant donné que chaque groupe a des variables de confusion similaires, toute différence en termes de résultat de santé au sein d’un groupe ne peut pas être attribuée à l’une des variables de confusion. Si toutes les variables de confusion importantes sont convenablement incluses dans le plan expérimental, la différence de résultat est due à la différence d’exposition (par exemple, la quantité d’exercice quotidien).

Néanmoins, en situation réelle, il est souvent impossible ou contraire à l’éthique de former des groupes expérimentaux contrôlés. Pour étudier l’effet de la pollution sur la dépression, par exemple, il n’est pas éthiquement acceptable d’exposer des personnes à une pollution élevée pour en apprécier les conséquences sur leur dépression. Vous pouvez seulement observer le niveau de pollution que des personnes ont déjà connu et leur taux de dépression. L’analyse d’inférence causale permet alors de modéliser la relation de causalité existant entre les données d’observation en imitant un plan expérimental contrôlé. Pour ce faire, on estime un score de propension pour chaque observation ; les scores de propension permettent d’estimer un jeu de pondérations d’équilibrage pour les observations. Les pondérations d’équilibrage sont configurées de telle sorte qu’elles préservent la relation de causalité entre les variables d’exposition et de résultat, mais qu’elles éliminent l’effet des variables de confusion sur la variation d’exposition, ce qui garantit une estimation non biaisée de la relation de causalité. Les observations pondérées obtenues possèdent des propriétés analogues à un jeu de données collecté via un ECR ; vous pouvez établir des inférences à partir de celui-ci de nombreuses façons tout comme vous pouvez le faire pour les jeux de données collectés via un plan expérimental.

Deux méthodes courantes permettent d’estimer les pondérations d’équilibrage : l’appariement des scores de propension et la pondération par l’inverse du score de propension. Lors de l’appariement du score de propension, chaque observation est appariée à diverses autres observations possédant des variables de confusion similaires (mesurées selon le degré de similitude de leurs scores de propension), mais des valeurs d’exposition différentes. En comparant la valeur de résultat d’une observation aux valeurs de résultat de ses appariements, vous pouvez voir quelle aurait été la valeur de résultat de l’observation si les expositions avaient été différentes. La pondération d’équilibrage attribuée à chaque observation est égale au nombre d’appariements de l’observation à une autre observation. Dans le cadre de la pondération par l’inverse du score de propension, les pondérations d’équilibrage sont attribuées en inversant les scores de propension et en multipliant par la probabilité globale de l’exposition. Cette procédure augmente la représentation des observations rares (observations dont le score de propension est faible) et diminue la représentation des observations courantes (scores de propension élevés) de sorte que la proportion de l’influence des variables de confusion est conservée dans toutes les valeurs de la variable d’exposition.

Les pondérations d’équilibrage issues de l’appariement des scores de propension et de la pondération par l’inverse du score de propension ne suffisent pas toujours à équilibrer les variables de confusion. Aussi, leurs corrélations pondérées sont calculées par comparaison à une valeur de seuil. Si les corrélations se trouvent sous le seuil (ce qui signifie que la corrélation est faible), elles sont considérées comme équilibrées et une ERF est estimée. Toutefois, si les pondérations d’équilibrage ne sont pas suffisantes pour équilibrer les variables de confusion, l’outil renvoie un message d’erreur et ne produit pas d’ERF.

Exemples d’application

Voici quelques exemples d’application de l’outil :

• Étudier dans quelle mesure l’exposition à la publicité pour des produits issus de l’industrie du tabac influe sur la consommation du tabac chez les adolescents aux États-Unis. Dans cet exemple, la variable d’exposition correspond au degré d’exposition à la publicité pour chaque adolescent et la variable de résultat à la quantité de tabac consommé par chaque adolescent sur une période donnée. Les variables de confusion désignent toute autre variable connue ou soupçonnée d’être liée à l’exposition ou à la consommation de tabac chez les adolescents comme des facteurs socio-économiques, une exposition directe aux produits du tabac du fait de la consommation de membres de la famille ou d’amis, le prix des produits du tabac et leur disponibilité. De nombreuses variables d’exposition peuvent être choisies pour examiner la consommation de tabac chez les adolescents (l’exposition directe aux produits du tabac liée à la consommation intrafamiliale, par exemple). Or, la publicité des produits du tabac est une variable d’exposition utile, car s’il s’avérait qu’elle était à l’origine d’une forte hausse de la consommation du tabac chez l’adolescent, il serait possible de réduire la quantité des publicités par voie réglementaire. Réduire la consommation des membres adultes de la famille serait, en revanche plus complexe.
• Estimez l’effet causal de la quantité d’engrais sur le rendement du maïs en agriculture de précision tout en contrôlant le type de sol, les techniques de production agricole, les variables environnementales et d’autres variables de confusion pour chaque parcelle. Par exemple, quelle quantité supplémentaire de maïs serait produite si chaque exploitation augmentait la dose d’engrais de 10 pour cent ?
• Estimez l’effet causal entre la pression artérielle et le risque d’infarctus en contrôlant les variables de confusion, telles que l’âge, le poids, les variables socio-démographiques et l’accès aux soins de santé.
• Dans le cadre des données spatiales, les distances par rapport à d’autres entités constituent souvent des variables d’exposition utiles. Par exemple, la distance par rapport aux magasins d’alimentation, aux espaces verts et aux hôpitaux entraînent la modification d’autres variables : résider loin d’un magasin d’alimentation réduit l’accès à la nourriture, résider loin d’un hôpital réduit l’accès aux soins, etc. Pour des raisons analogues, les variables spatiales et les distances par rapport à d’autres entités sont également des variables de confusion importantes même si les variables d’exposition et de résultat ne sont pas des variables spatiales.

En revanche, l’analyse d’inférence causale comporte un certain nombre de limites et postulats de départ à respecter pour que les estimations des effets de causalité ne soient pas biaisées et soient valides : Parmi les hypothèses et limites de l’analyse d’inférence causale figurent les suivantes :

• Toutes les variables de confusion importantes doivent être incluses. Il s’agit d’une hypothèse forte de l’analyse d’inférence causale. En d’autres termes, si des variables liées à la fois aux variables d’exposition et de résultat ne sont pas incluses en tant que variables de confusion, l’estimation de l’effet causal sera biaisée (mélange de l’effet causal et de l’effet de confusion des variables de confusion manquantes). L’outil n’est pas en mesure de déterminer si toutes les variables de confusion importantes ont été incluses, il est donc essentiel de prendre en compte celles que vous incluez. Si des variables de confusion importantes ne sont pas disponibles, interprétez les résultats avec précaution ou n’utilisez pas l’outil.
• Les corrélations existant entre les variables de confusion et la variable d’exposition doivent être supprimées de façon à isoler l’effet causal. En analyse d’inférence causale, la suppression des corrélations entre les variables de confusion et d’exposition est appelée équilibrage ; l’outil utilise diverses procédures d’équilibrage. Notez, toutefois, que l’équilibrage ne parvient pas toujours à éliminer un nombre suffisant de corrélations entre les variables de confusion et d’exposition. Si la procédure d’équilibrage n’équilibre pas assez les variables de confusion, l’outil renvoie un message d’erreur et n’estime pas l’ERF. Pour plus d’informations sur l’erreur et sur sa résolution, reportez-vous à la section Conseils pour obtenir des variables de confusion équilibrées.
• L’ERF ne peut pas extrapoler hors de la plage des valeurs d’exposition qui ont permis son estimation. Si, par exemple, la variable d’exposition est une température annuelle moyenne, vous ne pouvez pas estimer de nouveaux résultats pour des températures supérieures à celles qui figurent dans l’échantillon. Autrement dit, vous ne serez peut-être pas en mesure de prévoir les résultats futurs si les températures moyennes dépassent les températures moyennes actuelles. Par ailleurs, l’outil réduit (supprime de l’analyse) par défaut le pourcentage supérieur et inférieur des valeurs d’exposition : la plage de l’ERF sera encore plus étroite que les valeurs d’exposition des observations de l’échantillon.

Sorties de l’outil

L’outil créé une grande variété de sorties que vous pouvez utiliser pour explorer la relation de causalité entre les variables d’exposition et de résultat. Les résultats sont renvoyés sous forme d’une couche de graphiques, de messages de géotraitement, d’entités en sortie (ou d’une table) et d’une table ERF en sortie.

Fonction exposition-réponse

Le résultat principal de l’outil est l’ERF qui estime dans quelle mesure la variable de résultat réagit aux modifications de la variable d’exposition. L’ERF estime la nouvelle moyenne de population (la moyenne de tous les membres de la population) de la variable de résultat si tous les membres de la population ont adopté la même variable d’exposition, mais gardé leurs variables de confusion. Par exemple, pour l’ensemble des comtés des États-Unis, si la variable d’exposition correspond à l’indice PM2,5 (particules dont le diamètre est de 2,5 micron) et la variable de résultat au taux d’hospitalisations pour des problèmes d’asthme, l’ERF estime dans quelle mesure le taux d’hospitalisations national moyen liée à l’asthme évoluerait si le niveau national de PM2,5 augmentait ou diminuait, sans modifier les autres variables (telles que les variables sociodémographiques) présentes avant le changement de PM2,5.

Lorsqu’elle est exécutée dans une carte active, une couche de graphiques est ajoutée à la carte affichant l’ERF. La même image ERF apparaît également dans les messages.

L’ERF estime la valeur moyenne de la variable de résultat (axe y) si la même valeur d’exposition (axe x) était remplacée pour tous les membres de la population.

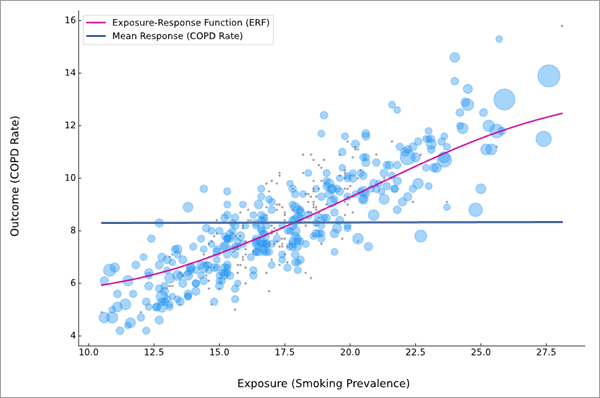
La courbe rose représente l’ERF entre les variables d’exposition (axe x) et les variables de résultat (axe y). Les observations sont visibles sous forme de bulles bleu clair dans l’arrière-plan du nuage de points. Les grandes bulles indiquent que l’entité a une pondération d’équilibrage plus importante et a davantage contribué à l’estimation de l’ERF. Dans le cadre de l’estimation du score de propension, si l’observation n’a pas de correspondance, elle s’affiche sous forme d’un point gris clair. Les observations réduites ne sont pas visibles sur le diagramme.

L’ERF contient également une ligne horizontale bleue indiquant la valeur moyenne de la variable de résultat afin de pouvoir comparer celle-ci à l’estimation moyenne des différents niveaux de la variable d’exposition. Par exemple, dans l’image ci-dessus, si tous les comtés avaient modifié leur prévalence de tabagisme et lui avaient attribué la même valeur inférieure à 17,5 environ (là où la ligne moyenne croise l’ERF), le taux global de bronchopneumopathie chronique obstructive (MPOC) aurait été inférieur au niveau actuel. De même, le taux de MPOC aurait augmenté si tous les comtés avaient modifié leur prévalence de tabagisme en lui attribuant une valeur supérieure à 17,5.

Vous pouvez également utiliser le paramètre Table en sortie de la fonction exposition-réponse pour créer une table de l’ERF. Si elle est créée, la table comporte 200 valeurs d’exposition équidistantes comprises entre l’exposition minimale et l’exposition maximale ainsi que la valeur de réponse correspondante. Si des valeurs d’exposition ou de résultat cibles sont fournies, celles-ci sont également ajoutées à la fin de la table ainsi que la valeur d’exposition ou de réponse estimée.

Statistiques d’équilibrage des variables de confusion

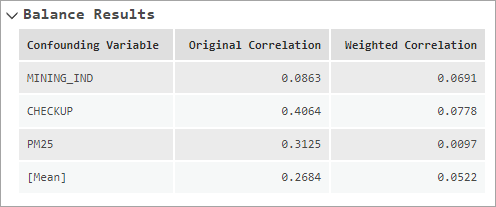
La section Résultats de l’équilibrage des messages affiche les corrélations absolues initiales et pondérées existant entre chaque variable de confusion et la variable d’exposition. Elle vous permet de voir si les pondérations d’équilibrage ont effectivement réduit la corrélation initiale entre les variables de confusion et la variable d’exposition. Dans le cas où les pondérations parviennent à un équilibrage, les corrélations pondérées doivent être inférieures aux corrélations initiales. La ligne finale de la table des messages présente la corrélation absolue moyenne, médiane ou maximale d’après la valeur du paramètre Type d’équilibrage.

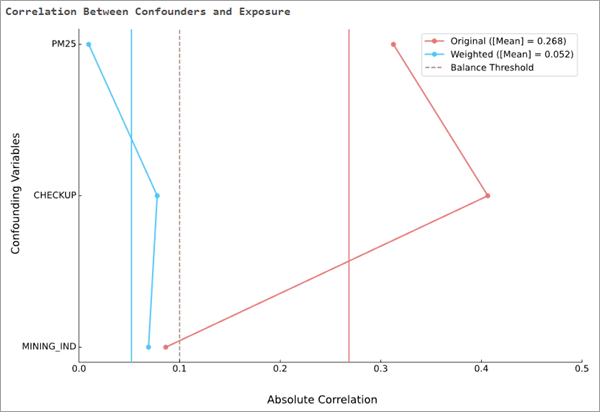
Le diagramme de message Corrélation entre les variables de confusion et l’exposition affiche les mêmes informations que la table, mais dans un diagramme linéaire vertical. Pour chaque variable de confusion, les corrélations initiales sont reliées par une ligne rouge et les corrélations pondérées par une ligne bleue. Les corrélations agrégées initiales et pondérées s’affichent également respectivement sous forme de barres verticales rouges et bleues. Si les pondérations équilibrent efficacement les variables de confusion, les lignes bleues se trouvent généralement à gauche des lignes rouges. Le seuil d’équilibrage est matérialisé par une ligne verticale en pointillés et indique à quel point les corrélations sont proches du seuil. Par exemple, dans l’illustration ci-dessous, deux des variables de confusion avaient des corrélations relativement élevées (au-dessus de 0,3 et de 0,4, respectivement) au départ, mais les pondérations d’équilibrage ont réduit les corrélations à moins de 0,1. La troisième variable de confusion avait au départ une faible corrélation (un peu moins de 0,1), mais les pondérations d’équilibrage ont encore réduit la corrélation. Dans l’ensemble, la corrélation moyenne a été réduite pour passer de près de 0,3 à moins de 0,1.

Pour obtenir plus d’informations sur l’équilibrage des variables de confusion, consultez la section Recherche de variables de confusion équilibrées ci-ci-après.

Résultats d’optimisation des paramètres

Les messages contiennent également des sections résumant divers paramètres d’optimisation utilisés pour l’estimation de l’ERF. En fonction des paramètres spécifiés dans l’outil, les sections suivantes peuvent être affichées :

• Résultats de la réduction — Le nombre initial d’observations (après suppression des enregistrements comportant des valeurs nulles), le nombre d’observations supprimées suite à la réduction de l’exposition, le nombre d’observations supprimées suite à la réduction du score de propension et le nombre final d’observations restantes après réduction sont affichés.
• Résultats de recherche dans la grille correspondants : pour l’appariement des scores de propension, les résultats de la recherche des paramètres d’appariement s’affichent. L’outil utilise différentes combinaisons du nombre de groupes d’exposition et de la pondération relative du score de propension par rapport à l’exposition (échelle) et affiche les corrélations pondérées obtenues pour chaque combinaison. La combinaison qui donne la corrélation pondérée la plus faible (meilleur équilibre) apparaît en gras.
• Résultats de l’équilibrage de la transformation : pour le modèle du score de propension par régression, les transformations des variables de confusion qui ont été utilisées pour tenter de parvenir à un équilibre, ainsi que la corrélation pondérée pour chaque combinaison de transformations, sont affichées. La combinaison de transformations qui donne la corrélation pondérée la plus faible (meilleur équilibre) apparaît en gras.
• Résultats de l’équilibrage du boosting de gradient : pour le modèle du score de propension par boosting de gradient, les résultats de la recherche du boosting de gradient dans la grille sont affichés. L’outil essaie neuf combinaisons du nombre d’arbres et de la vitesse d’apprentissage et affiche les corrélations pondérées pour chaque combinaison. La combinaison qui donne la corrélation pondérée la plus faible apparaît en gras.
• Paramètres engendrant le meilleur équilibre : pour l’appariement des scores de propension, le nombre de groupes d’exposition et la pondération relative du score de propension par rapport à l’exposition (échelle) qui a produit le meilleur équilibre des variables de confusion sont affichés. Pour le boosting de gradient, le nombre d’arbres, la vitesse d’apprentissage et la valeur initiale du générateur de nombres aléatoires aboutissant au meilleur équilibre sont affichés.
• Résultats de l’équilibrage : les corrélations initiales et pondérées pour chaque variable de confusion, ainsi que la corrélation moyenne, médiane ou maximale, sont affichées. Si des transformations ont été utilisées, la transformation est également affichée pour chaque variable de confusion.

Pour obtenir plus d’informations sur le nombre de valeurs déterminées dans les messages, reportez-vous à la section Estimation des paramètres d’équilibrage optimaux ci-après.

Entités en sortie

Les entités en sortie, ou la table, comportent des copies des variables d’exposition, de résultat et de confusion, ainsi que des scores de propension, des pondérations d’équilibrage (totaux d’appariements ou pondérations par l’inverse du score de propension) et un champ indiquant si l’enregistrement a été réduit. Lorsqu’elles sont ajoutées à une carte, les entités en sortie sont dessinées selon la pondération d’équilibrage. Cela permet de détecter un modèle spatial lié aux pondérations, ce qui peut être le signe que certaines régions sont surreprésentées ou sous-représentées dans les résultats.

Si vous fournissez une valeur d’exposition ou de résultat, chaque valeur fournie crée deux champs supplémentaires en sortie. Pour les valeurs d’exposition cibles, le premier champ contient la valeur de résultat estimée si l’observation a reçu l’exposition cible et le deuxième champ contient la modification estimée de la valeur de résultat. Les valeurs positives indiquent que la variable de résultat augmentera et les valeurs négatives qu’elle diminuera. Pour les valeurs de résultat cibles, le premier champ contient la valeur d’exposition qui génèrerait le résultat cible et le deuxième champ contient la modification à apporter à la valeur d’exposition pour produire le résultat cible.

Si vous créez des diagrammes contextuels affichant l’ERF locale, chaque enregistrement en sortie affiche l’ERF locale dans la fenêtre contextuelle. Les valeurs d’exposition ou de résultat cible sont visibles sous forme de triangles orange sur les axes x et y. Vous pouvez cliquer sur les triangles pour activer ou désactiver les barres horizontales ou verticales et voir l’emplacement où la valeur croise l’ERF locale. De plus, vous pouvez passer le curseur sur les triangles pour afficher les informations sur les modifications à apporter en termes d’exposition ou de résultat de manière à atteindre la cible. Pour plus d’informations, reportez-vous à la section Estimer les effets de causalité locaux.

Pour cette observation, la prévalence du tabagisme doit être réduite d’environ 1,5 pour atteindre le taux de MPOC cible fixé à 7.

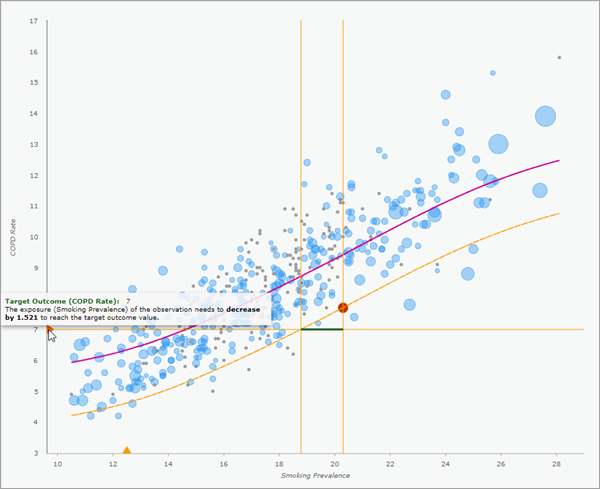
Si vous créez des intervalles de confiance bootstrap pour l’ERF, deux champs supplémentaires seront créés. Ils indiquent le nombre de sélections de l’observation dans l’échantillon bootstrap et le nombre d’inclusions de l’observation dans un échantillon bootstrap ayant atteint l’équilibre. Il est recommandé de rechercher d’éventuels modèles spatiaux pour les deux champs. Si certaines régions contiennent bien plus d’échantillons bootstrap équilibrés que d’autres, il se peut que les intervalles de confiance soient biaisés (ces derniers produisent généralement des intervalles de confiance trop étroits pour être réalistes). Pour plus d’informations, consultez la section Intervalles de confiance bootstrap.

Scores de propension

Le score de propension est un élément fondamental de l’analyse d’inférence causale. Un score de propension est défini comme la vraisemblance (ou la probabilité) qu’une observation prenne la valeur d’exposition observée, compte tenu des valeurs de ses variables de confusion. Un score de propension important indique que la valeur d’exposition de l’observation est courante parmi les personnes avec des variables de confusion similaires. À l’inverse, un faible score de propension indique qu’elle est rare parmi ces personnes. Considérons par exemple le cas d’une personne dont la pression artérielle est élevée (variable d’exposition) mais qui ne présente pas de facteurs de risque (variables de confusion) : cette personne aura probablement un score de propension faible car il est relativement rare d’avoir une pression artérielle élevée sans présenter de facteur de risque. À l’inverse, une personne dont la pression artérielle est élevée et qui présente de nombreux facteurs de risque aura un score de propension plus élevé puisque cette situation est courante.

Deux approches en matière d’analyse d’inférence causale utilisent le score de propension : l’appariement des scores de propension et la pondération par l’inverse du score de propension. Chaque approche affecte un jeu de pondérations d’équilibrage à chaque observation qui permet ensuite l’équilibrage des variables de confusion (voir la section Recherche de variables de confusion équilibrées ci-après pour en savoir plus).

Appariement des scores de propension

L’appariement des scores de propension essaie d’équilibrer les variables de confusion en appariant chaque observation à diverses observations possédant des variables d’exposition similaires, mais des expositions différentes. En comparant la valeur de résultat de l’observation aux résultats des observations appariées, vous pouvez voir quels auraient été les résultats de l’observation si elle avait été soumise à une exposition différente (tout en ayant gardé les mêmes variables de confusion). Après avoir trouvé des appariements pour toutes les observations, la pondération d’équilibrage attribuée à chaque observation est égale au nombre d’appariements de l’observation à une autre observation. Si, par exemple, une observation n’est pas l’appariement d’une autre observation, la pondération d’équilibrage est égale à zéro ; si l’observation correspond à n’importe quelle autre observation, la pondération d’équilibrage est égale au nombre d’observations.

L’appariement des scores de propension pour des variables d’exposition continues est relativement complexe. Vous trouverez sa description complète et son analyse dans les quatrième et cinquième points de la section Références ci-après. Vous trouverez ci-dessous un bref résumé de la procédure d’appariement :

La procédure commence par diviser les observations en groupes équidistants en fonction de la variable d’exposition (similaires aux groupes d’un histogramme) à l’aide de la valeur du paramètre Nombre de groupes d’exposition. L’appariement du score de propension est réalisé au sein de chaque groupe par comparaison des scores de propension du groupe aux scores de propension contrefactuels de toutes les observations. Un score de propension contrefactuel est un score de propension qu’une observation aurait si elle possédait les mêmes variables de confusion, mais des expositions différentes (dans le cas présent, les valeurs centrales de chaque groupe d’exposition). Les appariements de chaque groupe sont déterminés en trouvant l’observation du groupe d’exposition dont le score de propension est le plus proche des scores de propension contrefactuels de toutes les autres observations. Toutefois, comme les valeurs d’exposition des observations présentes dans le groupe ne sont généralement pas alignées au centre du groupe, une pénalité supplémentaire est ajoutée en fonction de la différence entre la valeur d’exposition et le centre du groupe d’exposition. Le degré de pénalisation est déterminé par la valeur du paramètre Pondération relative du score de propension par rapport à l’exposition (appelé paramètre d’échelle dans les documents de référence) ; l’appariement global est l’observation dont la somme pondérée des différences absolues de scores de propension (score de propension moins score de propension imaginaire) et d’exposition (exposition brute moins valeur centrale du groupe) est la plus faible.

Pondération par l’inverse du score de propension

La pondération par l’inverse du score de propension attribue des pondérations d’équilibrage à chaque observation en inversant les scores de propension et en multipliant par la probabilité globale d’atteindre l’exposition donnée. Cette approche de l’inférence causale donne des pondérations d’équilibrage plus élevées aux observations dont les scores de propension sont faibles et des pondérations d’équilibrage plus faibles aux observations dont les scores de propension sont élevés. Le raisonnement qui sous-tend ce schéma de pondération est que le score de propension est une mesure du degré de fréquence ou de rareté de la valeur d’exposition pour le jeu spécifique de variables de confusion. En augmentant l’influence (c’est-à-dire en augmentant la pondération d’équilibrage) des observations rares (observations avec un faible score de propension) et en diminuant l’influence des observations fréquentes, la proportion des distributions globales des variables de confusion est conservée dans toutes les valeurs de la variable d’exposition.

Remarque :

L’estimation de la densité de noyau (KDE) permet d’estimer la probabilité globale de la valeur d’exposition. Le KDE utilise un noyau Gaussien avec une bande passante de Silverman tel qu’il est implémenté dans la fonction scipy.stats.gaussian_kde du paquetage SciPy Python.

Estimation du score de propension

Le paramètre Méthode de calcul des scores de propension permet d’indiquer la façon dont les scores de propension sont estimés. Chaque méthode crée un modèle qui utilise les variables de confusion comme variables explicatives et la variable d’exposition comme variable dépendante. Deux méthodes de calcul des scores de propension sont disponibles :

• Régression : la régression des moindres carrés ordinaires permet d’estimer les scores de propension. 

  En savoir plus sur la régression des moindres carrés ordinaires

• Boosting de gradient : les arbres de régression du boosting de gradient permettent d’estimer les scores de propension.

  En savoir plus sur le boosting de gradient

Dans le cas du modèle de régression, des probabilités sont attribuées aux prévisions en supposant une distribution normale des résidus standardisés. Le modèle du boosting de gradient ne produit pas naturellement des résidus standardisés ; l’outil construit donc un second modèle de boosting de gradient pour prévoir la valeur absolue des résidus du premier modèle, qui fournit une estimation de l’erreur standard. L’estimation de la densité de noyau (identique à celle de la pondération par l’inverse du score de propension ci-dessus) est alors utilisée sur les résidus standardisés pour créer une distribution des résidus standardisés. Cette distribution peut ensuite être utilisée afin d’estimer les scores de propension pour toutes les combinaisons des valeurs de variables d’exposition et de confusion.

La régression et le boosting de gradient redimensionnent toutes les variables pour qu’elles soient comprises entre 0 et 1 avant de créer leur modèle respectif.

Recherche de variables de confusion équilibrées

Pour que l’ERF représente une estimation non biaisée de l’effet causal, toutes les variables de confusion doivent être incluses et équilibrées. En d’autres termes, les variables de confusion doivent être non corrélées à la variable d’exposition. Comme les variables de confusion et d’exposition sont corrélées par définition, les variables de confusion sont toujours déséquilibrées. Or, le but des pondérations d’équilibrage (issues de l’appariement du score de propension ou de la pondération par l’inverse du score de propension) consiste à pondérer chaque observation de telle manière que les observations pondérées s’équilibrent tout en conservant la relation entre les variables d’exposition et de résultat afin de garantir une estimation non biaisée de la fonction ERF.

Pour déterminer si les pondérations d’équilibrage équilibrent effectivement les variables de confusion, les corrélations pondérées sont calculées entre chaque variable de confusion et la variable d’exposition. Les valeurs absolues des corrélations pondérées sont alors agrégées et comparées à une valeur de seuil. Si la corrélation agrégée est inférieure au seuil, les variables de confusion sont jugées équilibrées. Vous pouvez spécifier le type d’agrégation (corrélation moyenne, médiane ou maximale) à l’aide du paramètre Type d’équilibrage et indiquer la valeur de seuil dans le paramètre Seuil d’équilibrage. Par défaut, l’outil calcule la corrélation moyenne absolue et utilise une valeur de seuil égale à 0,1.

Remarque :

Pour des variables de confusion continues, les corrélations pondérées sont calculées à l’aide du coefficient de corrélation de rang de Spearman pondéré. Cette corrélation est identique au coefficient de corrélation classique de Pearson, mais utilise des rangs pondérés des variables à la place de valeurs brutes. Avec l’utilisation des rangs, la corrélation est plus robuste vis-à-vis des valeurs aberrantes et des distributions de forme irrégulière. Pour les variables de confusion catégorielles, les corrélations pondérées sont calculées à l’aide d’une statistique êta pondérée qui utilise les rangs pondérés de la variable d’exposition. La statistique êta est un proche équivalent de la corrélation absolue de Pearson pour les variables catégorielles (les deux peuvent être définies comme la racine carrée de R-carré, le coefficient de détermination) et l’utilisation des rangs pondérés à la place des valeurs d’exposition brutes en fait un proche équivalent de la valeur absolue d’une corrélation de Spearman pondérée.

Conseils pour obtenir des variables de confusion équilibrées

Si les pondérations d’équilibrage ne sont pas suffisantes pour équilibrer les variables de confusion, l’outil renvoie une erreur et ne produit pas d’ERF. Néanmoins, divers messages affichent des informations sur les corrélations pondérées de chaque variable de confusion. Si vous rencontrez cette erreur, examinez les messages afin de déterminer dans quelle mesure les pondérations d’équilibrage ont réduit les corrélations et d’identifier la proximité de la corrélation pondérée par rapport au seuil d’équilibrage.

Si l’outil ne parvient pas à atteindre l’équilibre, vérifiez qu’il ne manque aucune variable de confusion pertinente et incluez les variables manquantes. Essayez ensuite différentes options pour les paramètres Méthode de calcul des scores de propension et Méthode d’équilibrage. Cependant, pour certains jeux de données, il se peut qu’aucune combinaison ne permette d’atteindre l’équilibre.

En général, plus les corrélations initiales des variables de confusion sont importantes, plus il est difficile de les équilibrer. Si les variables de confusion sont fortement corrélées, des échantillons de grande taille peuvent être nécessaires pour atteindre un équilibre suffisant. Dans le cas de variables de confusion catégorielles, plus le nombre de catégories est élevé, plus il est difficile de parvenir à un équilibre. Vous pouvez être amené à combiner certaines catégories, notamment en cas de faible variation de la variable d’exposition ou d’un petit nombre d’observations (moins de cinq habituellement) au sein de chaque catégorie.

Toutefois, si vous pouvez tolérer l’introduction d’un biais dans l’ERF, vous pouvez atteindre l’équilibre en augmentant le seuil d’équilibrage ou en utilisant un type d’équilibrage plus souple.

En général, une valeur faible de seuil d’équilibrage indique une moindre tolérance par rapport au biais lors de l’estimation de l’effet causal ; cependant, il est plus difficile d’atteindre l’équilibre avec des seuils bas. Dans le cas du type d’équilibrage, l’utilisation de la moyenne des corrélations garantit que les variables de confusion sont équilibrées en moyenne. Malgré cela, des variables de confusion peuvent encore présenter des corrélations élevées si elles sont suffisamment nombreuses à avoir des corrélations plus faibles pour faire passer la moyenne sous le seuil. L’option de la corrélation maximale est la plus prudente et implique que chaque variable de confusion se trouve sous le seuil. Cependant, si une seule variable de confusion est légèrement au-dessus du seuil, les variables de confusion seront considérées comme déséquilibrées. L’option de la corrélation médiane est la plus souple, car elle permet à environ la moitié des corrélations d’être très importantes tout en restant équilibrées.

Estimation des paramètres d’équilibrage optimaux

Réussir à équilibrer les variables de confusion est souvent une opération délicate. L’outil tente différentes optimisations et cherche à trouver des paramètres d’optimisation qui assurent des variables de confusion aussi équilibrées que possible. Les optimisations qui sont réalisées dépendent de divers paramètres de l’outil et sont décrites dans les sections suivantes.

Recherche des paramètres d’appariement

Lors de l’appariement des scores de propension, les résultats d’appariement dépendent des valeurs des paramètres Nombre de groupes d’exposition et Pondération relative du score de propension par rapport à l’exposition, mais il est difficile de prévoir les valeurs qui assureront le meilleur équilibre. De plus, de petites modifications apportées à l’une des valeurs peuvent conduire à des modifications importantes de l’autre valeur. Il est donc particulièrement difficile de trouver un couple de valeurs efficace. Si aucune valeur n’est fournie pour les paramètres, l’outil expérimente différentes combinaisons et affiche les résultats sous forme d’une table dans les messages. Dans la table, les lignes correspondent au nombre de groupes d’exposition et les colonnes aux pondérations relatives (souvent désignées sous le terme d’échelle). La corrélation pondérée de chaque combinaison apparaît dans la grille, toute combinaison ayant atteint l’équilibre est signalée par un astérisque à côté de la valeur. La combinaison qui donne la corrélation pondérée la plus faible (meilleur équilibre) apparaît en gras. Comme illustré dans l’image ci-dessous, les corrélations pondérées peuvent varier considérablement en fonction des valeurs des deux paramètres.

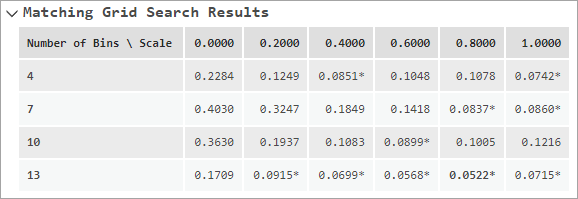
L’outil tente d’obtenir des pondérations relatives allant de 0 à 1 par incréments de 0,2, mais les nombres de groupes d’exposition qui sont testés dépendent du nombre d’observations. Les valeurs testées vont de la racine quatrième à deux fois la racine cubique du nombre d’observations. Les valeurs testées sont incrémentées de manière régulière d’au moins trois. 10 valeurs au maximum sont testées.

Transformations par régression

Lorsque vous utilisez la régression pour calculer les scores de propension, si les variables de confusion ne sont pas équilibrées, diverses transformations seront appliquées aux variables de confusion continues. Si, à tout moment, les variables de confusion atteignent l’équilibre, le traitement prend fin et le jeu actuel de transformations est utilisé pour créer l’ERF.

Le traitement commence par la variable de confusion la moins équilibrée (corrélation pondérée la plus importante) et applique une séquence de transformations. La transformation qui atteint le meilleur équilibre est conservée et le traitement se reproduit sur la variable de confusion suivante. Cela continue jusqu’à ce que toutes les variables de confusion soient testées avec toutes les transformations, et si les variables de confusion sont toujours déséquilibrées, l’outil renvoie un message d’erreur et ne produit pas d’ERF.

Les transformations suivantes sont réalisées, avec certaines restrictions sur les valeurs des variables de confusion transformées :

• Logarithme naturel : seulement pour les variables de confusion de valeur positive.
• Carré : seulement pour les variables de confusion de valeur non négative.
• Racine carrée : seulement pour les variables de confusion de valeur non négative.
• Cube
• Racine cubique

Les transformations qui ont engendré le meilleur équilibre apparaissent dans la section Résultats de l’équilibrage des messages ; l’historique complet des tentatives de transformation s’affiche dans la section Résultats de l’équilibrage de la transformation.

Dans le cas de l’appariement des scores de propension, le nombre de groupes d’exposition et les valeurs de pondération relative des variables de confusion initiales (non transformées) sont utilisés pour toutes les combinaisons de transformations. Cela vise à empêcher de très longs calculs par la répétition de la recherche des paramètres d’appariement pour chaque combinaison de transformations. La transformation Carré est limitée aux valeurs non négatives de sorte que le classement des valeurs d’exposition ne change pas avant et après la transformation, ce qui est primordial lors de la réutilisation du nombre de groupes d’exposition et de la pondération relative déterminés à partir des observations initiales.

Recherche de paramètres de boosting de gradient

Lorsque vous utilisez le boosting de gradient pour calculer les scores de propension, différentes combinaisons du nombre d’arbres et de la vitesse d’apprentissage sont testées. Si, à tout moment, les variables de confusion atteignent l’équilibre, le traitement prend fin et le nombre d’arbres et la vitesse d’apprentissage actuels sont utilisés. Le traitement essaie jusqu’à neuf combinaisons : le nombre d’arbres est égal à 10, 20 et 30 arbres et la vitesse d’apprentissage est égale à 0,1, 0,2, et 0,3.

Le nombre d’arbres et la vitesse d’apprentissages qui ont contribué au meilleur équilibre s’affichent dans la section Paramètres engendrant le meilleur équilibre, et l’historique complet des combinaisons de paramètres est visible dans la section Résultats de l’équilibrage du boosting de gradient.

Contrairement aux transformations issues des régressions, la recherche des paramètres d’appariement pour le nombre de groupes d’exposition et la pondération relative est répétée pour chaque combinaison d’arbres et de vitesse d’apprentissage. Une recherche approfondie est réalisée, car de petites fluctuations de l’un de ces quatre paramètres peuvent entraîner des modifications importantes des valeurs optimales des autres paramètres.

Estimation de la fonction exposition-réponse

La procédure d’équilibrage attribue des pondérations d’équilibrage (nombre d’appariements ou pondérations par l’inverse du score de propension) à chaque observation ; ces pondérations sont essentielles pour estimer la fonction exposition-réponse. Les observations pondérées (parfois appelées pseudo-population) possèdent chacune une valeur d’exposition, une valeur de résultat et une pondération, et l’objectif consiste à ajuster une courbe lissée (l’ERF) aux observations pondérées. Lors de l’estimation de l’ERF, chaque observation influence l’estimation proportionnellement à sa pondération. En d’autres termes, une observation avec une pondération égale à trois contribue autant que trois observations ayant chacune une pondération égale à un. De même, une observation dont la pondération est égale à zéro n’a pas d’impact sur l’ERF, ce qui a pour effet de l’écarter purement et simplement.

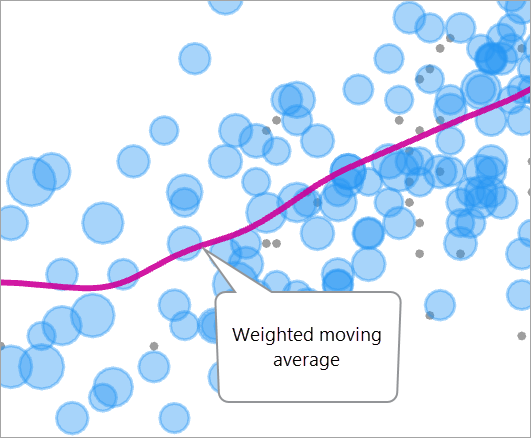
Pour une valeur donnée de la variable d’exposition (axe x), la valeur de réponse associée (axe y) est estimée comme une moyenne mobile pondérée (appelée parfois lisseur à noyau) des valeurs de résultat des observations. Les pondérations dans la moyenne pondérée sont les pondérations d’équilibrage multipliées par la pondération d’un noyau gaussien tronqué à trois écarts types.

Lorsque cette procédure est effectuée sur toutes les valeurs de la variable d’exposition, le résultat est une courbe lissée qui passe par toutes les observations et se rapproche des observations aux pondérations les plus élevées.

Estimation de la bande passante

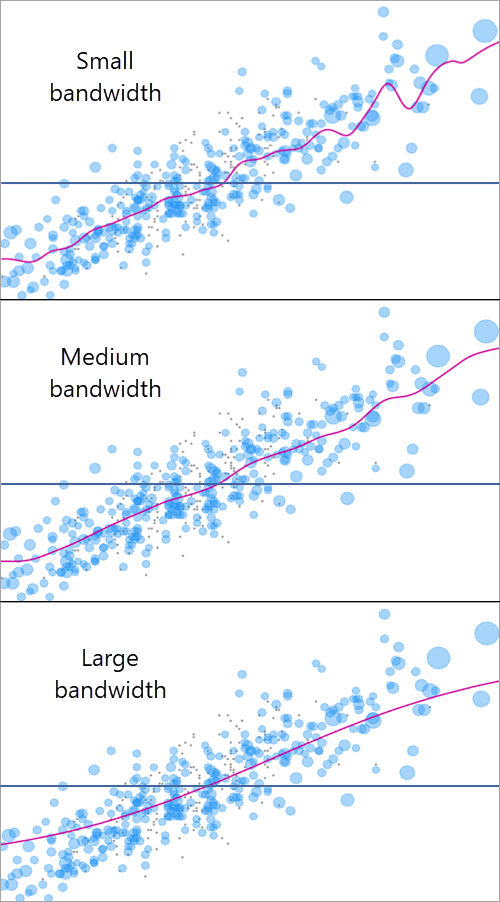
Le noyau dans la formule de la fonction exposition-réponse dépend d’une valeur de bande passante (écart type du noyau gaussien) qui contrôle le lissage de la courbe ERF ; la spécification d’une bande passante appropriée est cruciale pour produire une ERF à la fois précise et réaliste. Des valeurs plus élevées pour la bande passante produisent des ERF plus lisses pour un même ensemble d’observations pondérées. L’image suivante présente trois valeurs de bande passante utilisées pour les mêmes observations :

Vous pouvez utiliser le paramètre Méthode d’estimation de la largeur de bande pour sélectionner la manière d’estimer une valeur de bande passante. Trois méthodes d’estimation de la bande passante sont disponibles :

• Plug-in : une formule générale rapide est utilisée pour estimer une valeur de bande passante. Cette option, définie par défaut, permet un calcul rapide et produit généralement des ERF précises et réalistes. La méthode est une variante pondérée de la méthodologie de Fan (1996), elle dérive la valeur de la bande passante de la dérivée seconde d’un polynôme global pondéré de quatrième ordre ajusté à toutes les observations.
• Validation croisée : la valeur de bande passante qui minimise l’erreur quadratique moyenne de validation croisée est utilisée. Cette option est celle dont le calcul prend le plus de temps, mais elle est la plus pertinente en termes statistiques. Cependant, pour les jeux de données volumineux, la validation croisée a tendance à estimer des valeurs de bande passante trop faibles et génère des fonctions exposition-réponse trop courbes.
• Manuelle : la valeur de bande passante personnalisée fournie dans le paramètre Bande passante est utilisée. Cette option est recommandée si les autres options produisent des valeurs de bande passante aboutissant à des ERF trop lisses ou trop courbes. Dans ce cas, examinez les valeurs de bande passante estimées par les autres méthodes et apportez les corrections nécessaires pour ajuster le lissage.

La valeur de bande passante estimée est indiquée au bas des messages.

Remarque :

Dans le cas des méthodes de plug-in et de validation croisée, si la valeur de bande passante estimée est inférieure à l’écart le plus important entre les valeurs d’exposition, l’écart le plus important est estimé à la place. Cela permet de garantir que chaque valeur d’exposition dispose de suffisamment de données pour la moyenne pondérée. Pour utiliser des valeurs inférieures de bande passante, indiquez-les manuellement.

Estimer les effets de causalité locaux

Vous pouvez créer des ERF locales pour chaque enregistrement dans l’entité ou la table en sortie en cochant le paramètre Activer les fenêtres contextuelles de la fonction exposition-réponse. Une fois coché, la sortie comporte un graphique ERF dans les fenêtres contextuelles de chaque entité en sortie ou enregistrement de la table. Les fenêtres contextuelles montrent dans quelle mesure l’outil estime que la variable de résultat d’une observation donnée répond aux modifications de la variable d’exposition associée. L’ERF locale a la même forme que l’ERF globale, mais elle est décalée vers le haut ou le bas pour traverser l’observation considérée. De plus, si des valeurs de résultat ou d’exposition cibles sont fournies, elles apparaissent dans les diagrammes contextuels avec les modifications du résultat ou de l’exposition requises pour atteindre les cibles.

La création d’ERF locales ou encore l’utilisation de valeurs d’exposition ou de résultat cibles implique de formuler l’hypothèse supplémentaire d’un effet d’exposition fixe pour toutes les observations. Cette hypothèse est forte et sa violation peut déboucher sur des résultats biaisés ou qui induisent en erreur. L’hypothèse de l’effet d’exposition fixe signifie que l’effet de l’exposition sur le résultat est constant parmi tous les individus de la population. Autrement dit, compte tenu de leur exposition initiale, l’augmentation de l’exposition par une valeur fixe modifie le résultat de la même manière pour tous les membres, indépendamment des niveaux de toutes les autres variables (y compris, sans que cela soit limitatif, les valeurs de confusion mesurées). Par exemple, élever la quantité d’engrais de 150 lb par acre à 175 lb par acre augmenterait le rendement du maïs dans la même proportion pour toutes les exploitations, indépendamment de leur production actuelle, des techniques de production utilisées ou d’autres valeurs de confusion.

Cette hypothèse est raisonnable en l’absence de modificateurs d’effet, c’est-à-dire, de variables qui influent sur la façon dont le résultat répond à l’exposition au niveau individuel. Cela dit, les variables sociodémographiques telles que le sexe, la race ou le niveau d’éducation sont souvent des modificateurs d’effet négligés et sont généralement inclus en tant que variables de confusion dans les modèles d’inférence causale. Cela revient à établir la moyenne de la modification d’effet pour tous les niveaux de la variable de modification, ce qui assure une estimation d’un effet causal moyen global (l’ERF). En revanche, l’ERF globale ne représente pas un sous-groupe particulier défini par les niveaux du modificateur d’effet. Par exemple, un programme de formation professionnelle pourrait montrer que les offres d’emploi augmentent avec le nombre d’heures de formation. Or, les offres d’emploi plafonnent après un certain nombre d’heures de formation dans les quartiers noirs et hispaniques, ce qui suggère une potentielle discrimination systémique à l’embauche. Par conséquent, l’ERF globale peut masquer de façon involontaire les disparités auxquelles ces communautés font face. La fonction exposition-réponse globale représente l’effet d’exposition sur les résultats moyennés de l’ensemble de la population. Mais, en présence de variables modifiant l’effet, la fonction globale risque de ne pas représenter exactement l’effet d’exposition sur les résultats des zones majoritairement noires ou hispaniques.

Les ERF locales ne sont pas valides si le modèle contient des modificateurs d’effet. La stratification est l’une des approches utilisées pour traiter les modificateurs d’effet. Elle implique de diviser les observations en strates (ou sous-groupes) en se basant sur les valeurs de la variable modificatrice. En séparant les modificateurs d’effet par strate et en formant une ERF indépendante pour chaque strate, vous pouvez étudier séparément la relation existant entre l’exposition et le résultat au sein de chaque groupe. Cela permet de constater si l’effet de l’exposition sur le résultat diffère selon les différents niveaux du modificateur d’effet.

Intervalles de confiance bootstrap

Vous pouvez créer des intervalles de confiance de 95 pour cent pour l’ERF à l’aide du paramètre Créer des intervalles de confiance bootstrap. S’ils sont créés, les intervalles de confiance sont dessinés sous formes de lignes pointillées au-dessus et en dessous de l’ERF dans la couche de graphiques en sortie et les messages. Si une table ERF en sortie est créée, elle contient également les champs des limites de confiance supérieure et inférieure.

Les intervalles de confiance de 95 pour cent apparaissent au-dessus et en dessous de l’ERF sous forme de lignes pointillées.

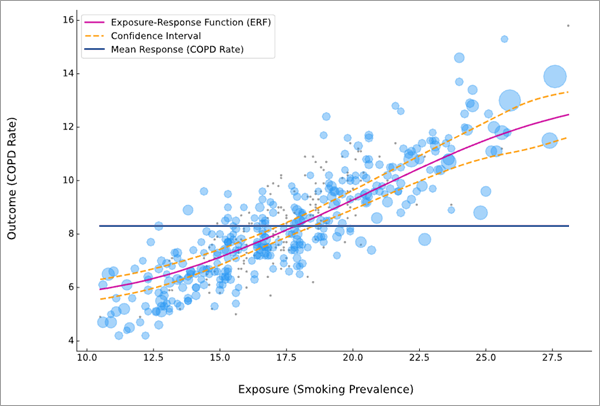
Les intervalles de confiance établissent les limites de la moyenne de la population de la variable de résultat pour une valeur donnée de la variable d’exposition. Comme la moyenne de la population est moins variable que les membres qui la composent, la plupart des points du nuage de points ne se situent généralement pas dans les intervalles de confiance, mais ce n’est pas une anomalie. Pour des raisons analogues, les intervalles de confiance ne sont applicables qu’à la fonction ERF globale et ne peuvent pas s’appliquer à une ERF locale.

Les intervalles de confiance sont créés à l’aide du bootstrap m-out-of-n. Cette procédure repose sur un échantillonnage aléatoire de M observations parmi N observations, pour lequel M=2*sqrt(N), comme recommandé par DasGupta (2008). L’outil exécute ensuite l’algorithme entier (recherche des paramètres optimaux, estimation des scores de propension, test d’équilibrage et estimation de l’ERF) sur l’échantillon bootstrap aléatoire. L’ERF obtenue est habituellement similaire à l’ERF initiale, sans être parfaitement identique. En reproduisant ce traitement à de nombreuses reprises, vous constaterez à quel point l’ERF varie pour des échantillons aléatoires d’observations différents. La variation des ERF obtenues explique la création des intervalles de confiance.

Si un échantillon bootstrap n’atteint pas l’équilibre (tel qu’il est déterminé par le type et le seuil d’équilibrage), l’échantillon bootstrap est écarté. L’outil poursuit les bootstraps jusqu’à ce que 5*sqrt(N) échantillons bootstrap atteignent l’équilibre. Cette valeur est dérivée de sorte que chaque observation doit être incluse dans au moins 10 échantillons bootstrap équilibrés en moyenne. Cette méthode permet des estimations stables des limites supérieure et inférieure pour la plage entière d’exposition. Si malgré les 25*sqrt(N) tentatives de bootstrap, les échantillons bootstrap sont toujours insuffisamment équilibrés, aucun intervalle de confiance n’est créé et un message d’avertissement est renvoyé.

Bien que les intervalles de confiance capturent de nombreuses sources d’incertitude de l’ERF, il est important de noter que pour créer des intervalles de confiance qui correspondent véritablement aux limites inférieure et supérieure de l’effet causal, il est nécessaire de tenir compte de toutes les sources potentielles d’incertitude. La procédure bootstrap de cet outil intègre l’incertitude de la procédure d’équilibrage et de l’estimation de l’ERF, mais elle n’est pas en mesure de prendre en compte les autres sources d’incertitude possibles, telles que l’imprécision des valeurs des variables ou le choix de la forme fonctionnelle de l’ERF (une moyenne mobile pondérée plutôt qu’une spline ou un polynôme global, par exemple). Par ailleurs, les intervalles de confiance deviennent arbitrairement étroits au fur et à mesure que vous augmentez le nombre d’observations, mais n’en tirez pas la conclusion que l’ERF caractérise parfaitement l’effet causal.

Lorsque des intervalles de confiance bootstrap sont créés, les entités en sortie ou la table contiennent deux champs associés aux amorçages. Le premier champ inclut le nombre de sélections de l’observation dans un échantillon bootstrap et le deuxième le nombre d’inclusions de l’observation dans un échantillon bootstrap qui a atteint l’équilibre et qu’une ERF a été estimée. Ces champs sont créés même en cas de nombre insuffisant d’échantillons bootstrap atteignant l’équilibre pour déterminer des intervalles de confiance. Pour les entités en sortie, les valeurs de la première colonne doivent présenter peu de modèles spatiaux, hormis autour du périmètre des entités. S’il existe des modèles spatiaux dans le deuxième champ, c’est le signe qu’un traitement spatial n’a peut-être pas été pris en compte. Si, par exemple, les échantillons bootstrap les plus équilibrés proviennent de certaines régions des données, ces régions sont surreprésentées dans les intervalles de confiance et ceux-ci sont exagérément étroits. Si vous observez des modèles spatiaux dans les nombres totaux des échantillons bootstrap équilibrés, envisagez d’inclure une variable de confusion spatiale (comme une région géographique) pour prendre en compte l’effet spatial omis.

Pour les tables en entrée, chaque bootstrap sélectionne M observations de manière aléatoire et uniforme. L’échantillonnage est réalisé avec remise de sorte que la même observation peut être sélectionnée plusieurs fois au cours de la même opération bootstrap. Pour les entités en entrée, les échantillons bootstrap sont générés en sélectionnant une seule entité au hasard et en l’incluant, avec ses huit plus proches voisines, dans l’échantillon. Cette sélection aléatoire se reproduit avec remise jusqu’à ce qu’au moins M observations soient incluses dans l’échantillon bootstrap. Les mêmes entités peuvent être sélectionnées de façon aléatoire à plusieurs reprises et incluses en tant que voisines plusieurs fois. L’utilisation de voisinages aléatoires au lieu d’une sélection complètement aléatoire contribue à corriger des facteurs de confusion spatiaux non mesurés (mais nous vous encourageons à corriger les facteurs de confusion spatiaux en intégrant des variables spatiales en tant que variables de confusion).

Puisque l’ERF ne peut pas s’étendre en dehors de la plage des valeurs d’exposition utilisée pour la créer, l’ERF de chaque échantillon bootstrap ne sera créé qu’entre l’exposition minimale et maximale des observations dans l’échantillonnage aléatoire. Par conséquent, les valeurs d’exposition les plus élevées et les plus basses se trouvent rarement dans la plage des valeurs échantillonnées de manière aléatoire. Un nombre inférieur d’ERF bootstrap est créé pour les valeurs d’exposition les plus extrêmes.

Une fois les bootstraps terminés, des intervalles de confiance de 95 pour cent sont créés en supposant une distribution T des valeurs de l’ERF bootstrap pour chaque valeur d’exposition. La variance des valeurs ERF est redimensionnée en les multipliant par (m/n) pour ajuster les seules valeurs m d’échantillonnage ; le degré de liberté est le nombre d’ERF bootstrap qui pourrait être généré pour la valeur d’exposition, moins un. De plus, les largeurs des intervalles de confiance sont lissées à l’aide du même lisseur à noyau que celui utilisé pour estimer l’ERF initiale (pondérations égales avec bande passante de plug-in). La largeur lissée est ensuite ajoutée et soustraite de l’ERF initiale pour produire les limites de confiance supérieure et inférieure. Si une table ERF en sortie est créée, elle contient les champs avec l’écart type lissé (largeur lissée divisée par la valeur critique) et le nombre d’ERF bootstrap qui pourraient être générées pour la valeur d’exposition.

Bibliographie

DasGupta, Anirban. 2008. « Asymptotic Theory of Statistics and Probability. » Biometrics. 64: 998-998. https://doi.org/10.1111/j.1541-0420.2008.01082_16.x

Fan, Jianquin. 1996. « Local Polynomial Modeling and Its Applications: Monographs on Statistics and Applied Probability 66. » (1st ed.). Routledge. https://doi.org/10.1201/9780203748725.

Imbens, Guido and Donald B. Rubin. 2015. « Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction. » Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9781139025751.

Khoshnevis, Naeem, Xiao Wu, and Danielle Braun. 2023. « CausalGPS: Matching on Generalized Propensity Scores with Continuous Exposures. » R package version 0.4.0. https://CRAN.R-project.org/package=CausalGPS.

Wu, Xiao, Fabrizia Mealli, Marianthi-Anna Kioumourtzoglou, Francesca Dominici, and Danielle Braun. 2022. « Matching on Generalized Propensity Scores with Continuous Exposures. » Journal of the American Statistical Association. https://doi.org/10.1080/01621459.2022.2144737.