Fonctionnement de l'outil Statistiques focales

L’outil Statistiques focales effectue une opération qui calcule une statistique pour les cellules en entrée dans un ensemble de fenêtres ou de voisinages superposés. La statistique (par exemple, la moyenne, le maximum ou la somme) est calculée pour toutes les cellules en entrée contenues dans chaque voisinage.

Traitement de voisinage

Théoriquement, l’algorithme traite chaque cellule du raster en entrée et calcule une statistique pour les cellules qui figurent dans la forme de voisinage spécifiée environnante. La cellule pour laquelle la statistique est calculée est appelée « cellule de traitement ». La valeur de la cellule de traitement est généralement incluse dans le calcul des statistiques de voisinage, mais selon la forme du voisinage, il est possible qu’elle n’y figure pas. Puisque les voisinages se superposent lors de la numérisation, les cellules en entrée qui sont incluses dans le calcul d’une cellule de traitement peuvent également contribuer au calcul d’une autre cellule de traitement.

Plusieurs formes de voisinage prédéfinies sont disponibles à la sélection. Vous pouvez également créer une forme personnalisée. Les statistiques que vous pouvez calculer pour un voisinage sont les suivantes : majorité, maximum, moyenne, médiane, minimum, centile, plage, écart type, somme et variété.

Exemple de calcul

À titre d’exemple de traitement d’un voisinage avec l’outil Statistiques focales, calculons une somme du voisinage autour de la cellule de traitement ayant pour valeur 5 dans le diagramme ci-après. Une forme de voisinage rectangulaire de 3 x 3 cellules est spécifié et le paramètre Ignorer NoData dans les calculs est conservé comme paramètre sélectionné par défaut. La somme des valeurs des cellules voisines (3 + 2 + 3 + 4 + 2 + 1 + 4 = 19) plus la valeur de la cellule de traitement (5) égale 24 (19 + 5 = 24). La valeur 24 est attribuée dans le raster en sortie à la cellule située au même emplacement que la cellule de traitement dans le raster en entrée.

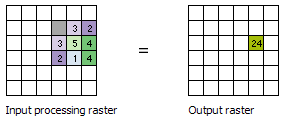
Le diagramme ci-dessus montre comment les calculs sont effectués sur une seule cellule du raster en entrée. Dans le diagramme suivant, les résultats sont indiqués pour toutes les cellules en entrée. Les cellules entourées de jaune identifient la même cellule de traitement et le même voisinage que dans l'exemple ci-dessus.

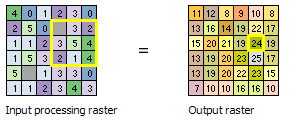
Cellules NoData

Le paramètre Ignorer les valeurs NoData dans les calculs contrôle la façon dont les cellules NoData sont traitées dans la fenêtre de voisinage. Si ce paramètre est activé (ignore_nodata = "DATA" dans Python), toutes les cellules du voisinage dont la valeur est NoData sont ignorées dans le calcul de la valeur en sortie de la cellule de traitement. S’il est désactivé (ignore_nodata = "NODATA" dans Python) et qu'une cellule d’un voisinage possède une valeur NoData, la valeur en sortie de la cellule de traitement est NoData.

Si la cellule de traitement elle-même est de type NoData et que l’option Ignorer NoData dans les calculs est sélectionnée, la valeur en sortie de la cellule est calculée en fonction des autres cellules du voisinage présentant une valeur valide. Si toutes les cellules du voisinage sont de type NoData, la sortie est de type NoData.

Cellules d’angle et de tronçon

Lorsque la cellule de traitement est proche des angles et des tronçons du raster en entrée, le nombre de cellules incluses dans le voisinage est ajusté en conséquence. Le calcul de statistique est également ajusté.

Les diagrammes suivants illustrent la manière dont la statistique en sortie est calculée pour chaque cellule de traitement à partir des cellules disponibles de chaque voisinage individuel. Le traitement commence à l’angle supérieur gauche du raster en entrée et procède à la numérisation de la gauche vers la droite sur chaque ligne avant de passer à la ligne suivante. Le voisinage utilisé dans cet exemple est un rectangle de 3 x 3 cellules et la statistique est une somme. Le paramètre Ignorer NoData dans les calculs est conservé comme le paramètre sélectionné par défaut. Dans les diagrammes, le voisinage est indiqué en jaune et la cellule de traitement en cyan.

Dans le cas de la première cellule de traitement, puisqu’elle figure à l’angle supérieur gauche du raster en entrée de 6 x 6 cellules, seules quatre cellules sont disponibles pour figurer dans le voisinage. La somme de ces valeurs permet d’obtenir une valeur en sortie de la première cellule égale à 11. Pour la cellule suivante située à droite, six cellules figurent désormais dans le voisinage et la somme est calculée pour ces cellules. La numérisation traite toutes les cellules de la première ligne. Dans un souci de gain de place, toutes les cellules de traitement ne sont pas représentées.

Le voisinage (présenté en jaune) autour de chaque cellule de traitement (en cyan) indique les cellules en entrée (haut) qui sont utilisées pour le calcul de la valeur de statistique en sortie (bas).

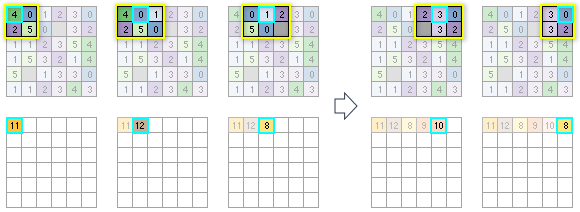
Notez que dans la première ligne, pour la troisième cellule de traitement à partir de la gauche (valeur = 1), une des cellules en entrée a une valeur NoData. Puisque l’outil a été défini pour ignorer les valeurs NoData, cette cellule particulière sera ignorée dans les calculs. Si la statistique à calculer avait été définie sur Moyenne à la place de Somme, elle aurait été calculée comme la somme de toutes les cellules dans le voisinage différentes de NoData, divisée par 5.

Pour la seconde ligne de cellules en entrée, la statistique de la première cellule de traitement est calculée sur la base de six cellules disponibles dans le voisinage. Pour la cellule de traitement suivante, neuf cellules sont à prendre en compte dans le calcul. Pour la cellule suivante, le calcul prend en compte huit valeurs en entrée, puisque l’une des cellules dans le voisinage de 3 x 3 cellules est de type NoData. Le traitement se poursuit pour le reste des cellules de la ligne, puis pour les lignes suivantes jusqu’à ce que toutes les cellules de traitement soient analysées.

Le voisinage, la cellule de traitement et la valeur en sortie d’une partie de la seconde ligne de cellules en entrée sont identifiés.

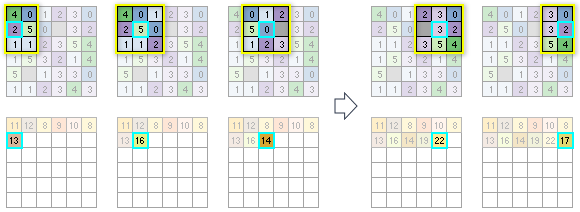
Taille du voisinage et performances

L’outil peut traiter des voisinages très volumineux. Toutefois, l’augmentation de la taille du voisinage aura un impact sur les performances car un plus grand nombre de cellules en entrée sera inclus dans chaque calcul. Le voisinage de type rectangle dispose de certaines optimisations qui améliorent les performances par rapport à d’autres formes de voisinage pour une zone donnée.

Quelle que soit la dimension, la taille maximale d’un voisinage est limitée à 4 096 cellules. En d’autres termes, les voisinages rectangulaires ne peuvent pas dépasser ce nombre de cellules, que ce soit dans le sens horizontal ou vertical. Pour les voisinages circulaires, le rayon ne peut pas dépasser 2 047 cellules.

Types de voisinage

La forme d’un voisinage peut être un anneau, un cercle, un rectangle ou un secteur. Vous pouvez également utiliser un fichier de noyau pour définir une forme de voisinage personnalisée et appliquer des pondérations différentes à certaines cellules du voisinage avant le calcul de la statistique.

La présentation ci-dessous décrit les différentes formes de voisinage et la manière dont elles sont définies :

• Anneau
  • La forme en anneau se compose de deux cercles, l’un étant situé à l’intérieur de l’autre pour former un anneau. Les cellules dont le centre est situé à l’extérieur du rayon du petit cercle, mais à l’intérieur du rayon du grand cercle sont incluses dans le traitement du voisinage. La surface qui se trouve entre les deux cercles constitue le voisinage en anneau.
  • Le rayon est représenté en unités de cellule ou de carte et est mesuré perpendiculairement à l’axe x ou y. Lorsque les rayons sont indiqués en unités de carte, ils sont convertis en unités de cellule. Les rayons obtenus en unités de cellule produisent une surface qui représente le plus fidèlement possible la surface calculée à l’aide des rayons d’origine en unités de carte. Les centres de cellule englobés par l’anneau sont inclus dans le traitement du voisinage.
  • Le voisinage en anneau par défaut présente un rayon intérieur d’une cellule et un rayon extérieur de trois cellules.
  • Voici une illustration d’exemple d’un voisinage en anneau :

  

  Une cellule de traitement avec le voisinage en anneau par défaut (rayon interne = 1 cellule, rayon externe = 3 cellules).

• Cercle
  • Un voisinage circulaire est créé en spécifiant une valeur de rayon.
  • Le rayon est représenté en unités de cellule ou de carte et est mesuré perpendiculairement à l’axe x ou y. Lorsque le rayon est indiqué en unités de carte, une logique supplémentaire est utilisée pour déterminer quelles cellules font partie du voisinage de traitement. D’abord, la surface exacte d’un cercle défini par la valeur de rayon spécifiée est calculée. Ensuite, la surface est calculée pour deux cercles supplémentaires, un où la valeur de rayon spécifiée est arrondie au nombre inférieur et un autre où elle est arrondie au nombre supérieur. Après comparaison de ces deux surfaces avec celle obtenue à partir du rayon spécifié, le rayon de la surface la plus proche est utilisé dans l’opération.
  • Le rayon du voisinage circulaire par défaut comporte trois cellules.
  • Voici une illustration d’exemple d’un voisinage circulaire :

  

  Cellule de traitement avec un voisinage circulaire (rayon = 2 cellules).

• Rectangle
  • Le voisinage rectangulaire est spécifié en fournissant une largeur et une hauteur en unités de cellule ou de carte.
  • Seules les cellules dont le centre est compris dans l’objet défini sont traitées dans le cadre du voisinage rectangulaire.
  • Le voisinage rectangulaire par défaut est un carré avec une hauteur et une largeur de trois cellules.
  • La position x,y de la cellule de traitement dans le voisinage, par rapport au coin supérieur gauche de ce dernier, est définie à l'aide des équations suivantes :

    x = (largeur du voisinage + 1)/2 y = (hauteur du voisinage + 1)/2

    Si le nombre de cellules en entrée est pair, les coordonnées x,y sont calculées à l’aide d’une troncature. Par exemple, dans un voisinage de 5 x 5 cellules, les valeurs de x et y sont 3,3. Dans un voisinage de 4 x 4, les valeurs de x et y sont 2,2.

  • Voici des illustrations d’exemples de deux voisinages rectangulaires :

  

  Cellule de traitement avec deux voisinages rectangulaires différents.

• Secteur
  • Un secteur est un voisinage en forme de camembert défini par un rayon, un angle de départ et un angle d’arrivée.
  • Il s’étend dans le sens anti-horaire, de l’angle de départ vers l’angle d’arrivée. Les angles sont exprimés en degrés arithmétiques de 0 à 360, où 0 est l’axe x positif (3h00 sur une horloge), et peuvent être des valeurs entières ou à virgule flottante. Vous pouvez utiliser des angles négatifs.
  • Le rayon est représenté en unités de cellule ou de carte et est mesuré perpendiculairement à l’axe x ou y. Lorsque le rayon est indiqué en unités de carte, il est converti en unités de cellule. Le rayon obtenu en unités de cellule produit une surface qui représente le plus fidèlement possible la surface calculée à l’aide des rayons d’origine en unités de carte. Les centres de cellule englobés par le secteur sont inclus dans le traitement du voisinage.
  • Le voisinage sectoriel par défaut s’étend de 0 à 90 degrés, avec un rayon de trois cellules.
  • Voici une illustration d’exemple d’un voisinage sectoriel :

  

  Cellule de traitement avec le voisinage sectoriel par défaut (rayon = 3 cellules, angle de départ = 0, angle d’arrivée = 90).

• Irrégulière
  • Permet de spécifier un voisinage de forme irrégulière autour de la cellule de traitement.
  • Le fichier de noyau irrégulier spécifie les positions de cellule à inclure dans le voisinage.
  • La position x,y de la cellule de traitement dans le voisinage, par rapport au coin supérieur gauche de ce dernier, est définie à l'aide des équations suivantes :

    x = (largeur + 1)/2 y = (hauteur + 1)/2

    Si le nombre de cellules en entrée est pair, les coordonnées x et y sont calculées à l'aide d'une troncature.

  • Les règles suivantes s'appliquent à un fichier de noyau avec un voisinage irrégulier :
    • Un fichier de noyau irrégulier est un fichier texte ASCII qui définit les valeurs et la forme d’un voisinage irrégulier. Le fichier peut être créé à l’aide de n’importe quel éditeur de texte. Il doit posséder une extension de fichier .txt.
    • La première ligne spécifie la largeur et la hauteur du voisinage (le nombre de cellules dans la direction x, suivi d’un espace, et le nombre de cellules dans la direction y).
    • Les lignes suivantes définissent la valeur à utiliser pour chaque position dans le voisinage qu'elles représentent. Les valeurs sont séparées par un espace.
    • Les valeurs définissent si une position dans le voisinage est incluse dans le calcul. En général, la valeur 1 permet d'identifier les positions à inclure dans les calculs d'un voisinage irrégulier, mais toute valeur positive ou négative non nulle peut être utilisée. Des valeurs à virgule flottante peuvent également être utilisées.
    • Pour exclure un emplacement du voisinage du calcul, utilisez la valeur 0 (et non un espace) à l'emplacement correspondant dans le fichier de noyau.

  • L’exemple ci-dessous montre un fichier de noyau irrégulier ASCII avec le voisinage correspondant :

  

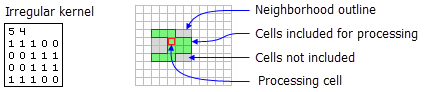
  Illustration d’un noyau de voisinage irrégulier et des cellules incluses dans le traitement.

• Pondération
  • Semblable au type de voisinage irrégulier, le voisinage de pondération vous permet non seulement de définir un voisinage irrégulier autour de la cellule de traitement, mais également d’appliquer des pondérations aux valeurs en entrée.
  • Le fichier de noyau pondéré spécifie les positions de cellule à inclure dans le voisinage et les pondérations par lesquelles elles sont multipliées.
  • Vous ne pouvez employer le voisinage pondéré qu’avec des statistiques de type moyenne, écart type et somme.
  • La position x,y de la cellule de traitement dans le voisinage, par rapport au coin supérieur gauche de ce dernier, est définie à l'aide des équations suivantes :

    x = (largeur + 1)/2 y = (hauteur + 1)/2

    Si le nombre de cellules en entrée est pair, les coordonnées x et y sont calculées à l'aide d'une troncature.

  • Les règles suivantes s’appliquent dans le cas d’un fichier de noyau pour un voisinage de type pondération :
    • Un fichier de noyau pondéré est un fichier texte ASCII qui définit les valeurs et la forme d’un voisinage pondéré. Le fichier peut être créé à l’aide de n’importe quel éditeur de texte. Il doit posséder une extension de fichier .txt.
    • La première ligne spécifie la largeur et la hauteur du voisinage (le nombre de cellules dans la direction x, suivi d’un espace, et le nombre de cellules dans la direction y).
    • Les lignes suivantes définissent la valeur à utiliser pour chaque position dans le voisinage qu'elles représentent. Les valeurs sont séparées par un espace.
    • Pour la statistique de somme, une pondération peut correspondre à toute valeur entière positive ou négative, ou valeur à virgule flottante.
    • Pour les statistiques de moyenne et d'écart type, une pondération peut correspondre à toute valeur entière positive ou valeur à virgule flottante. Les valeurs négatives n'étant pas autorisées pour ces statistiques, toute position dont la pondération est négative est ignorée dans les calculs.
    • Pour exclure un emplacement du voisinage du calcul, utilisez la valeur 0 (et non un espace) à l'emplacement correspondant dans le fichier de noyau.

  • L'exemple ci-dessous montre le contenu d'un fichier de noyau pondéré avec le voisinage correspondant :

  

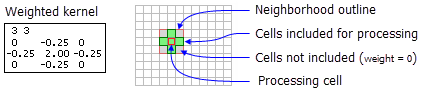
  Illustration d’un noyau de voisinage pondéré et des cellules incluses dans le traitement.

Types de statistiques

Les statistiques disponibles sont les suivantes : majorité, maximum, moyenne, médiane, minimum, minorité, centile, plage, écart type, somme et variété. Le type de statistique par défaut est la moyenne.

Certains types de statistiques sont disponibles uniquement lorsque le raster en entrée est de type entier.

• Majorité
  • Vous ne pouvez utiliser qu’un raster de type entier en entrée.
  • La fréquence de chaque valeur de cellule unique dans chaque voisinage est déterminée. Si une valeur unique est dotée de la fréquence la plus élevée (ce qui est le plus fréquent), cette valeur est attribuée à toutes les cellules de ce voisinage. En cas d'égalité, la plus faible des valeurs de fréquence égale est attribuée, sauf si la valeur de la cellule de traitement correspond à l’une des égalités. Dans ce cas, la valeur d’origine de la valeur de la cellule de traitement est renvoyée.
• Maximum
  • Si le raster en entrée est de type entier, le raster en sortie contient des nombres entiers. Si les valeurs en entrée sont à virgule flottante, les valeurs en sortie sont également à virgule flottante.
• Moyenne
  • L’entrée peut être un raster de type entier ou à virgule flottante.
  • Le raster en sortie est toujours à virgule flottante.
  • Pour le type de voisinage de pondération, il s'agit de l'un des sous-ensembles de types de statistiques pris en charge. Pour en savoir plus sur le mode de calcul de cette statistique, reportez-vous à la section Voisinage pondéré.
• Médiane
  • L’entrée peut être un raster de type entier ou à virgule flottante.
  • Le raster en sortie est toujours à virgule flottante.
  • Si le nombre de valeurs de cellule valides dans le voisinage est impair, la valeur médiane est calculée en sélectionnant la valeur centrale du classement des valeurs. Si le nombre de valeurs dans le voisinage est pair, la valeur médiane est calculée en faisant la moyenne des deux valeurs centrales du classement des valeurs.
• Minimum
  • Si le raster en entrée est de type entier, le raster en sortie contient des nombres entiers. Si les valeurs en entrée sont à virgule flottante, les valeurs en sortie sont également à virgule flottante.
• Minorité
  • Vous ne pouvez utiliser qu’un raster de type entier en entrée.
  • La fréquence de chaque valeur de cellule unique dans chaque voisinage est déterminée. Si une valeur unique est dotée de la fréquence la plus basse (ce qui est le moins fréquent), cette valeur est attribuée à toutes les cellules de ce voisinage. En cas d'égalité, la plus faible des valeurs de fréquence égale est attribuée, sauf si la valeur de la cellule de traitement correspond à l’une des égalités. Dans ce cas, la valeur d’origine de la valeur de la cellule de traitement est renvoyée.
• Centile
  • L’entrée peut être un raster de type entier ou à virgule flottante.
  • Le raster en sortie est toujours à virgule flottante.
  • Le résultat de la statistique de pourcentage est calculé selon la formule suivante (Hyndman and Fan, 1996) :

    pk = (k-1)/(n-1)

• Plage
  • Si le raster en entrée est de type entier, le raster en sortie contient des nombres entiers. Si les valeurs en entrée sont à virgule flottante, les valeurs en sortie sont également à virgule flottante.
  • Les valeurs de chaque emplacement de cellule dans le raster en sortie sont déterminées cellule par cellule par la formule : Focal Range = Focal Maximum – Focal Minimum
• Écart type
  • Le raster en sortie est toujours à virgule flottante.
  • Pour le type de voisinage de pondération, il s'agit de l'un des sous-ensembles de types de statistiques pris en charge. Pour en savoir plus sur le mode de calcul de cette statistique, reportez-vous à la section Voisinage pondéré.
  • L’écart type est calculé sur la population entière (méthode N). Il ne repose pas sur un échantillon (méthode N-1).
• Somme
  • Si le raster en entrée est de type entier, le raster en sortie contient des nombres entiers. Si les valeurs en entrée sont à virgule flottante, les valeurs en sortie sont également à virgule flottante.
  • Pour le type de voisinage de pondération, il s'agit de l'un des sous-ensembles de types de statistiques pris en charge. Pour en savoir plus sur le mode de calcul de cette statistique, reportez-vous à la section Voisinage pondéré.
• Variété
  • Vous ne pouvez utiliser qu’un raster de type entier en entrée.

Calculs de voisinage pondéré

Vous pouvez appliquer des pondérations pour ajuster l’influence de chaque valeur du voisinage sur le résultat final de la cellule de traitement.

Les sections suivantes indiquent les formules utilisées pour calculer les résultats des statistiques de moyenne pondérée, d’écart type et de somme. Chaque formule est illustrée par un exemple qui indique les calculs pour une cellule de traitement et les résultats pour un voisinage en forme de rectangle de 3 x 3 cellules.

Statistique de moyenne pondérée

Dans le cas du voisinage pondéré avec la statistique de moyenne, la valeur en sortie d’une cellule de traitement centrale correspond à la somme des produits des valeurs de pondération du noyau multipliées par les valeurs en entrée, divisée par la somme des valeurs de pondération du noyau.

La formule appliquée aux cellules d'un voisinage est la suivante :

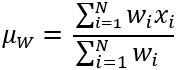
Où :

• µ_W représente la valeur de la moyenne pondérée de la population pour la cellule de traitement.
• N représente le nombre de cellules dans le voisinage.
• w_i représente une valeur de pondération définie dans le noyau.
• x_i représente une valeur de cellule en entrée.

Héritage :

Dans les versions précédentes, les calculs utilisaient le nombre de cellules dans le voisinage comme dénominateur.

Les valeurs de pondération doivent être des valeurs positives et peuvent être entières ou à virgule flottante.

Exemple

Soit une cellule de traitement ayant pour valeur 7 et ses huit voisins environnants :

4 6 7 6 7 8 4 5 6

La moyenne mathématique (somme/nombre) de ces valeurs est 53/9 = 5,889.

Soit le noyau de cellules pondéré 3 x 3 suivant :

3 3 0,0 0,5 0,0 0,5 2,0 0,5 0,0 0,5 0,0

Ce noyau donne le degré d’influence le plus élevé à la cellule centrale (pondération égale à 2), réduit l’influence des quatre voisins orthogonaux de la cellule de traitement (pondération égale à 0,5) et fait en sorte que les quatre cellules des coins n’aient aucune influence (pondération égale à 0).

Si l'on applique l’équation de moyenne pondérée fournie ci-avant, le calcul permettant d'obtenir la valeur finale est le suivant :

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) / (w1 + w2 + w3 + w4 + w5 + w6 + w7 + w8 + w9) = ((0*4)+(0,5*6)+(0*7)+(0,5*6)+(2,0*7)+(0,5*8)+(0*4)+(0,5*5)+(0*6)) / (0+0,5 + 0 + 0,5 + 2,0 + 0,5 + 0 + 0,5 + 0) = (0 + 3,0 + 0 + 3,0 + 14,0 + 4,0 + 0 + 2,5 + 0) / (0,5 + 0,5 + 2,0 + 0,5 + 0,5) = (3,0 + 3,0 + 14,0 + 4,0 + 2,5) / 4,0 = 26,5 / 4,0 = 6,625

En comparaison, la moyenne standard des neuf cellules en entrée serait de 5,889. Si seules les cinq cellules en entrée qui se trouvent à l'intérieur du noyau (où la pondération est de zéro) sont incluses, mais que les valeurs des pondérations ne sont pas prises en compte, la moyenne devient 6,4 (6 + 6 + 7 + 8 + 5 = 32, ensuite divisé par cinq).

Statistique de l’écart type pondéré

Dans le cas du voisinage de pondération avec la statistique d’écart type, la valeur en sortie d’une cellule de traitement est le résultat de l’équation suivante :

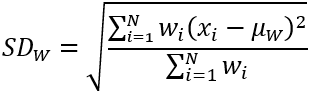
Où :

• SD_W représente la valeur de l'écart type pondéré de la population pour la cellule de traitement.
• µ_W représente la valeur de la moyenne pondérée de la population pour la cellule de traitement.
• N représente le nombre de cellules dans le voisinage.
• w_i représente une valeur de pondération définie dans le noyau.
• x_i représente une valeur de cellule en entrée.

Les valeurs de pondération doivent être des valeurs positives et peuvent être entières ou à virgule flottante.

Si toutes les valeurs en entrée d’un voisinage sont identiques, la valeur de l’écart type pour cette cellule de traitement est 0.

Exemple

Les valeurs de voisinage utilisées dans l’exemple de la moyenne pondérée ci-avant sont à nouveau utilisées dans cet exemple.

4 6 7 6 7 8 4 5 6

Les mêmes valeurs de noyau pondéré sont également utilisées :

3 3 0,0 0,5 0,0 0,5 2,0 0,5 0,0 0,5 0,0

Si l'on applique l’équation de l’écart type pondéré fournie ci-avant pour la cellule de traitement centrale de valeur 7, le résultat du calcul de l’écart type pondéré est d’environ 0,85696.

Statistique de somme pondérée

Dans le cas du voisinage de pondération avec la statistique de somme, la valeur en sortie d’une cellule de traitement est le résultat de l’équation suivante :

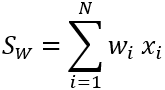
Où :

• S_W représente la valeur de la somme pondérée pour la cellule de traitement.
• N représente le nombre de cellules dans le voisinage.
• w_i représente une valeur de pondération définie dans le noyau.
• x_i représente une valeur de cellule en entrée.

Les valeurs de pondération peuvent être des valeurs positives ou négatives et être entières ou à virgule flottante.

Exemple

Prenons l’exemple des valeurs de voisinage suivantes en entrée :

4 6 7 6 7 8 4 5 6

Soit le noyau de cellules pondéré 3 x 3 suivant :

3 3 -1 -2 -1 0 0 0 1 2 1

Si l'on applique l’équation fournie ci-avant, le calcul utilisé pour obtenir la valeur finale est le suivant :

= (w1x1 + w2x2 + w3x3 + w4x4 + w5x5 + w6x6 + w7x7 + w8x8 + w9x9) = ((-1*4) + (-2*6) + (-1*7) + (0*6) + (0*7) + (0*8) + (1*4) + (2*5) + (1*6)) = (-4) + (-12) + (-7) + 4 + 10 + 6 = -3

Bibliographie

• Hyndman, R.J. and Y. Fan, November 1996. "Sample Quantiles in Statistical Packages." The American Statistician 50 (4) : 361-365.